4.4: حركة القذيفة

أهداف التعلم

• استخدم الحركة أحادية البعد في الاتجاهات العمودية لتحليل حركة المقذوف.
• احسب المدى ووقت الرحلة والارتفاع الأقصى للقذيفة التي تم إطلاقها والتي تؤثر على سطح أفقي مسطح.
• أوجد وقت الطيران وسرعة الارتطام لمقذوف يهبط على ارتفاع مختلف عن ارتفاع الإطلاق.
• احسب مسار المقذوف.

حركة المقذوفات هي حركة جسم يتم إلقاؤه أو إسقاطه في الهواء، ويخضع فقط للتسارع نتيجة للجاذبية. تتعدد تطبيقات حركة المقذوفات في الفيزياء والهندسة. تشمل بعض الأمثلة النيازك عند دخولها الغلاف الجوي للأرض والألعاب النارية وحركة أي كرة في الرياضة. تسمى هذه الأشياء المقذوفات ويسمى مسارها بالمسار. حركة الأجسام الساقطة كما تمت مناقشتها في الحركة على طول خط مستقيم هي نوع بسيط أحادي البعد من حركة المقذوفات التي لا توجد فيها حركة أفقية. في هذا القسم، ننظر في حركة المقذوفات ثنائية الأبعاد، ويهمل علاجنا آثار مقاومة الهواء.

أهم حقيقة يجب تذكرها هنا هي أن الحركات على طول المحاور العمودية مستقلة وبالتالي يمكن تحليلها بشكل منفصل. لقد ناقشنا هذه الحقيقة في متجهات الإزاحة والسرعة، حيث رأينا أن الحركات الرأسية والأفقية مستقلة. مفتاح تحليل حركة المقذوفات ثنائية الأبعاد هو تقسيمها إلى حركتين: واحدة على طول المحور الأفقي والأخرى على طول المحور الرأسي. (اختيار المحاور هذا هو الأكثر منطقية لأن التسارع الناتج عن الجاذبية عمودي؛ وبالتالي، لا يوجد تسارع على طول المحور الأفقي عندما تكون مقاومة الهواء ضئيلة.) كما هو معتاد، نسمي المحور الأفقي المحور السيني والمحور الرأسي المحور y. ليس مطلوبًا أن نستخدم هذا الاختيار من المحاور؛ إنه مناسب ببساطة في حالة تسارع الجاذبية. في حالات أخرى، قد نختار مجموعة مختلفة من المحاور. \(\PageIndex{1}\)يوضح الشكل رمز الإزاحة، حيث نُعرِّف\(\vec{s}\) الإزاحة الكلية،\(\vec{y}\) وهي المتجهات المكونة لها على طول المحاور الأفقية والعمودية، على التوالي.\(\vec{x}\) مقادير هذه المتجهات هي s و x و y.

الشكل\(\PageIndex{1}\): إجمالي الإزاحة لكرة القدم عند نقطة على طول مسارها. \(\vec{s}\)يحتوي المتجه على مكونات\(\vec{x}\) وعلى\(\vec{y}\) طول المحاور الأفقية والعمودية. حجمه هو s وهو يصنع زاوية\(\phi\) بالأفقي.

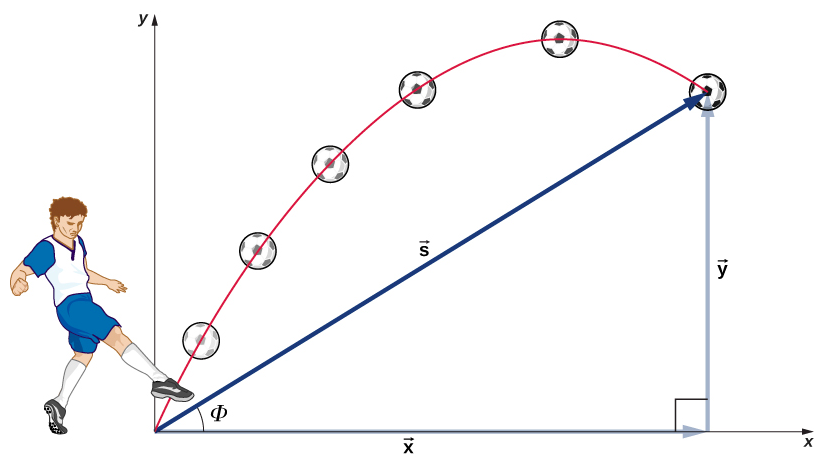
لوصف حركة المقذوفات بالكامل، يجب علينا تضمين السرعة والتسارع، وكذلك الإزاحة. يجب أن نجد مكوناتها على طول المحاور x- و y. لنفترض أن جميع القوى باستثناء الجاذبية (مثل مقاومة الهواء والاحتكاك، على سبيل المثال) لا تكاد تذكر. عند تحديد الاتجاه الإيجابي للصعود، تكون مكونات التسارع بسيطة جدًا:

\[a_{y} = −g = −9.8\; m/s^{2} (− 32\; ft/s^{2}) \ldotp\]

نظرًا لأن الجاذبية عمودية، a _x = 0. إذا كانت a _x = 0، فهذا يعني أن السرعة الأولية في اتجاه x تساوي السرعة النهائية في الاتجاه x، أو v _x = v _0x. باستخدام هذه الشروط المتعلقة بالعجلة والسرعة، يمكننا كتابة المعادلة الحركية 4.11 حتى المعادلة 4.18 للحركة في مجال الجاذبية المنتظم، بما في ذلك بقية المعادلات الحركية لعجلة ثابتة من الحركة ذات التسارع الثابت. تصبح المعادلات الحركية للحركة في مجال الجاذبية المنتظم معادلات حركية بـ _y = −g، a _x = 0:

حركة أفقية

\[v_{0x} = v_{x}, \quad x = x_{0} + v_{x} t \label{4.19}\]

حركة عمودية

\[y = y_{0} + \frac{1}{2} (v_{0y} + v_{y})t \label{4.20}\]

\[v_{y} = v_{0y} - gt \label{4.21}\]

\[y = y_{0} + v_{0y} t - \frac{1}{2} g t^{2} \label{4.22}\]

\[v_{y}^{2}= v_{0y}^{2} + 2g(y − y_{0}) \label{4.23}\]

باستخدام هذه المجموعة من المعادلات، يمكننا تحليل حركة المقذوفات، مع مراعاة بعض النقاط المهمة.

إستراتيجية حل المشكلات: حركة المقذوفات

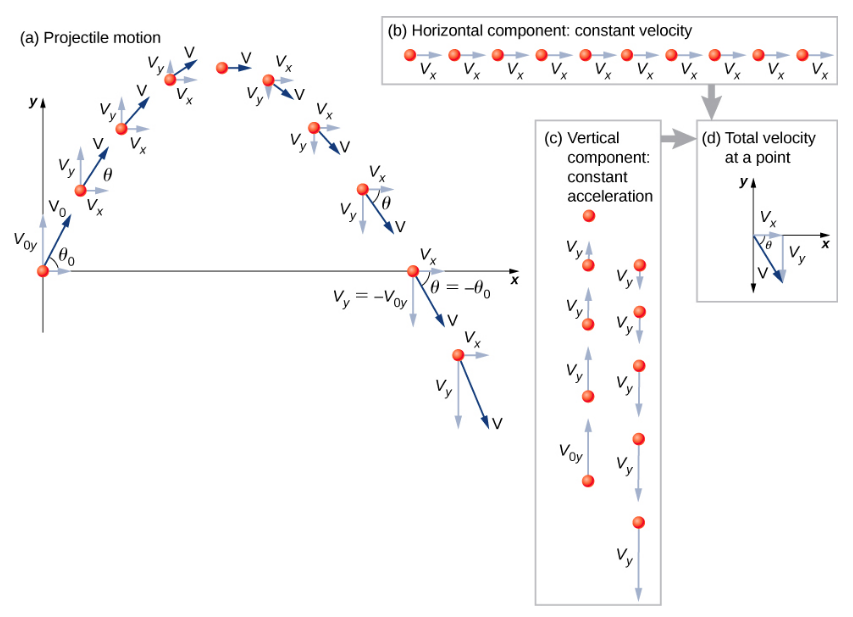
1. قم بحل الحركة إلى مكونات أفقية وعمودية على طول المحاور x- و y. مقادير مكونات الإزاحة\(\vec{s}\) على طول هذه المحاور هي x و y، ومقادير مكونات السرعة\(\vec{v}\) هي v _x = vcos\(\theta\) و v _y = vsin\(\theta\)، حيث v هو حجم السرعة\(\theta\) واتجاهها بالنسبة إلى الأفقي، كما هو موضح في الشكل\(\PageIndex{2}\).
2. تعامل مع الحركة كحركتين مستقلتين أحادية البعد: واحدة أفقية والأخرى عمودية. استخدم المعادلات الحركية للحركة الأفقية والعمودية المعروضة سابقًا.
3. حل المشكلات المجهولة في الحركتين المنفصلتين: واحدة أفقية والأخرى رأسية. لاحظ أن المتغير المشترك الوحيد بين الحركات هو time t. إجراءات حل المشكلات هنا هي نفسها تلك الخاصة بمعادلات الحركة أحادية البعد ويتم توضيحها في الأمثلة المحلولة التالية.
4. أعد تجميع الكميات في الاتجاهين الأفقي والعمودي لإيجاد إجمالي الإزاحة\(\vec{s}\) والسرعة\(\vec{v}\). حل لحجم واتجاه الإزاحة والسرعة باستخدام $s =\ sqrt {x^ {2} + y^ {2}}\ ldotp\ quad\ phi =\ tan^ {-1}\ اليسار (\ dfrac {y} {x}\ اليمين)،\ رباعية v =\ sqrt {v_ {x} ^ {2}\ ldotp {2}\ ldotp {2} $$أين\(\phi\) هو اتجاه النزوح\(\vec{s}\).

الشكل\(\PageIndex{2}\): (أ) نقوم بتحليل حركة المقذوفات ثنائية الأبعاد عن طريق تقسيمها إلى حركتين مستقلتين أحادية البعد على طول المحاور الرأسية والأفقية. (ب) الحركة الأفقية بسيطة، لأن a _x = 0 و v _x هي حركة ثابتة. (ج) تبدأ السرعة في الاتجاه الرأسي في الانخفاض مع ارتفاع الجسم. في أعلى نقطة، تكون السرعة الرأسية صفرًا. عندما يسقط الجسم نحو الأرض مرة أخرى، تزداد السرعة الرأسية مرة أخرى من حيث الحجم ولكنها تشير في الاتجاه المعاكس للسرعة الرأسية الأولية. (د) يُعاد تجميع حركتي x و y لإعطاء السرعة الكلية في أي نقطة معينة على المسار.

مثال 4.7: قذيفة الألعاب النارية تنفجر عالياً وبعيدًا

أثناء عرض الألعاب النارية، يتم إطلاق قذيفة في الهواء بسرعة أولية قدرها 70.0 متر/ثانية بزاوية 75.0 درجة فوق الأفقي، كما هو موضح في الشكل\(\PageIndex{3}\). تم ضبط المصهر لإشعال الغلاف بمجرد وصوله إلى أعلى نقطة فوق الأرض. (أ) احسب الارتفاع الذي تنفجر عنده القذيفة. (ب) كم من الوقت يمر بين إطلاق القذيفة والانفجار؟ (ج) ما هي الإزاحة الأفقية للقشرة عندما تنفجر؟ (د) ما هو إجمالي النزوح من نقطة الإطلاق إلى أعلى نقطة؟

الشكل\(\PageIndex{3}\): مسار قذيفة الألعاب النارية. تم إعداد المصهر لتفجير القذيفة عند أعلى نقطة في مسارها، والتي وُجد أنها تقع على ارتفاع 233 مترًا و125 مترًا أفقيًا.

إستراتيجية

يمكن تقسيم الحركة إلى حركات أفقية وعمودية تكون فيها a _x = 0 و _y = −g، ويمكننا بعد ذلك تعريف x ₀ و y ₀ ليكونا صفرًا وحل الكميات المطلوبة.

الحل

1. نعني بـ «الارتفاع» الارتفاع أو الوضع الرأسي y فوق نقطة البداية. يتم الوصول إلى أعلى نقطة في أي مسار، تسمى القمة، عندما v _y = 0. نظرًا لأننا نعرف السرعات الأولية والنهائية، بالإضافة إلى الموضع الأولي، فإننا نستخدم المعادلة التالية للعثور على y: $$v_ {y} ^ {2} = v_ {0y} ^ {2} - 2g (y - y_ {0})\ ldotP$لأن y ₀ و v _y كلاهما صفر، يتم تبسيط المعادلة إلى $0 = v_ {0y} ^ {2} - 2gy\ LdotP$$حل لعطائي $$y =\ frac {v_ {0y} ^ {2} {2g}\ ldotP$$الآن يجب أن نجد v _0y، مكون السرعة الأولية في الاتجاه y. يتم إعطاؤه بواسطة v _0y = v ₀ sin\(\theta_{0}\)، حيث v ₀ هي السرعة الأولية البالغة 70.0 m/s و\(\theta_{0}\) = 75° هي الزاوية الأولية. وهكذا $$v_ {0y} = v_ {0}\ sin\ theta = (70.0\; م/ث)\ sin 75^ {o} = 67.6\; م/s $و y هو $y =\ frac {(67.6\; م/ث) ^ {2} {2} {2 (9.80\ م/س ^ {2})}}\ lDotp $$وهكذا، لدينا $y = 233\ م\ ldotP$$لاحظ أنه نظرًا لأن الارتفاع إيجابي، فإن السرعة الرأسية الأولية إيجابية، وكذلك الحد الأقصى للارتفاع، ولكن التسارع الناتج من الجاذبية سلبية. لاحظ أيضًا أن الحد الأقصى للارتفاع يعتمد فقط على المكون الرأسي للسرعة الأولية، بحيث يصل أي مقذوف يحتوي على مكون رأسي أولي للسرعة يبلغ 67.6 متر/ثانية إلى ارتفاع أقصى يبلغ 233 مترًا (مع إهمال مقاومة الهواء). الأرقام الواردة في هذا المثال معقولة لشاشات الألعاب النارية الكبيرة، التي تصل أصدافها إلى هذه الارتفاعات قبل أن تنفجر. من الناحية العملية، لا تكون مقاومة الهواء ضئيلة تمامًا، لذلك يجب أن تكون السرعة الأولية أكبر إلى حد ما من تلك المعطاة للوصول إلى نفس الارتفاع.
2. كما هو الحال في العديد من المشكلات الفيزيائية، هناك أكثر من طريقة لحل الوقت الذي يصل فيه المقذوف إلى أعلى نقطة. في هذه الحالة، أسهل طريقة هي استخدام v _y = v _0y − gt. نظرًا لأن v _y = 0 في القمة، فإن هذه المعادلة تقلل $0 = v_ {0y} - gt$$أو $$t =\ frac {v_ {0y}} {g} =\ frac {67.6\; m/s} {9.80\; م/s^ {2}} = 6.90\ s\ lDotP$$هذا الوقت معقول أيضًا للألعاب النارية الكبيرة. إذا كنت قادرًا على رؤية إطلاق الألعاب النارية، فلاحظ مرور عدة ثوانٍ قبل أن تنفجر القذيفة. هناك طريقة أخرى للعثور على الوقت وهي استخدام y = y ₀ +\(\frac{1}{2}\) (v _0y + v _y) t، وهذا متروك لك كتمرين لإكماله.
3. نظرًا لأن مقاومة الهواء ضئيلة، فإن a _x = 0 والسرعة الأفقية ثابتة، كما تمت مناقشته سابقًا. الإزاحة الأفقية هي السرعة الأفقية مضروبة في الوقت كما هو موضح في x = x ₀ + v _x t، حيث x ₀ يساوي صفرًا. وهكذا، $x = v_ {x} t، $$حيث v _x هو المكون x للسرعة، والذي يُعطى بـ $v_ {x} = v_ {0}\ cos\ theta = (70.0\؛ م/ث)\ cos 75^ {o} = 18.1\؛ م/ث\ lDotP$$الوقت t لكلتا الحركتين هو نفسه، لذا x هو $x = (18.1\; م/ثانية) (6.DotP$$/s) 90\; s) = 125\; m\ lDotP$الحركة الأفقية هي سرعة ثابتة في غياب مقاومة الهواء. يمكن أن يكون الإزاحة الأفقية الموجودة هنا مفيدة في منع شظايا الألعاب النارية من السقوط على المتفرجين. عندما تنفجر القذيفة، يكون لمقاومة الهواء تأثير كبير، وتهبط العديد من الأجزاء تحتها مباشرة.
4. تم حساب المكونات الأفقية والعمودية للإزاحة للتو، لذلك كل ما هو مطلوب هنا هو العثور على حجم واتجاه الإزاحة عند أعلى نقطة: $$\ vec {s} = 125\ قبعة {i} + 233\ قبعة {j} $$|\ vec {s} | | =\ sqrt {125^ {2} + 233^ {2}} = 264\؛ m$$$\ theta\ tan ^ {-1}\ يسار (\ dfrac { 233} {125}\ اليمين) = 61.8^ {o}\ lDotP$لاحظ أن زاوية متجه الإزاحة أقل من زاوية الإطلاق الأولية. لمعرفة سبب ذلك، راجع الشكل\(\PageIndex{1}\) الذي يوضح انحناء المسار نحو مستوى الأرض. عند حل المثال 4.7 (a)، يكون التعبير الذي وجدناه لـ y صالحًا لأي حركة مقذوف عندما تكون مقاومة الهواء ضئيلة. اتصل بالحد الأقصى للارتفاع y = h. ثم، $h =\ frac {v_ {0y} ^ {2}} {2g}\ ldotP$$تحدد هذه المعادلة الحد الأقصى لارتفاع المقذوف فوق موضع الإطلاق وتعتمد فقط على المكون الرأسي للسرعة الأولية.

التمرين 4.3

رُميت صخرة أفقيًّا من منحدر ارتفاعه ١٠٫٠ م بسرعة ١٥٫٠ م/ث. (أ) حدِّد أصل النظام الإحداثي. (ب) ما المعادلة التي تصف الحركة الأفقية؟ (ج) ما المعادلات التي تصف الحركة الرأسية؟ (د) ما هي سرعة الصخرة عند نقطة الارتطام؟

مثال 4.8: حساب حركة القذيفة - لاعب التنس

يفوز لاعب تنس بمباراة في ملعب آرثر آش ويضرب كرة في المدرجات بسرعة ٣٠ م/ث وبزاوية ٤٥ درجة فوق الأفقي (الشكل\(\PageIndex{4}\)). في طريقها لأسفل، يلتقط المتفرج الكرة على ارتفاع 10 أمتار فوق النقطة التي أصيبت فيها الكرة. (أ) احسب الوقت الذي تستغرقه كرة التنس للوصول إلى المتفرج. (ب) ما مقدار واتجاه سرعة الكرة عند الارتطام؟

الشكل\(\PageIndex{4}\): مسار كرة التنس التي اصطدمت بالمدرجات.

إستراتيجية

مرة أخرى، يتيح لنا حل هذه الحركة ثنائية الأبعاد في حركتين مستقلتين أحادية البعد حل الكميات المطلوبة. يخضع الوقت الذي تقضيه المقذوف في الهواء لحركته الرأسية وحدها. وبالتالي، نقوم بحلها أولاً. بينما ترتفع الكرة وتهبط عموديًا، تستمر الحركة الأفقية بسرعة ثابتة. يطلب هذا المثال السرعة النهائية. وبالتالي، نعيد تجميع النتائج الرأسية والأفقية للحصول عليها\(\vec{v}\) في الوقت النهائي t، المحددة في الجزء الأول من المثال.

الحل

1. عندما تكون الكرة في الهواء، فإنها ترتفع ثم تسقط إلى الموضع النهائي أعلى بـ 10.0 متر من ارتفاع البداية. يمكننا إيجاد الوقت لذلك باستخدام المعادلة\ ref {4.22}: $y = y_ {0} + v_ {0y} t -\ frac {1} {2} gt^ {2}\ ldotP$إذا اتخذنا الموضع الأولي y ₀ ليكون صفرًا، فإن الموضع النهائي هو y = 10 م. السرعة الرأسية الأولية هي المكون الرأسي للسرعة الأولية: $v_ {0y} = v_ {0}\ sin\ theta_ {0} = (30.0\; م/ث)\ sin 45^ {o} = 21.2\; m/s\ lDotP$$الاستبدال في المعادلة\ المرجع {4.22} لأن y يعطينا 10.0 دولار\; م = (21.2\; م/ث) t − (4.90\; م/s^ {2}) t^ {2}\ lDotP$$إعادة ترتيب المصطلحات تعطي معادلة تربيعية في t $: $ (4.90\; م/s^ {2}) t^ {2} - (21.2\; م/ث) t + 10.0\; m = 0\ lDotP$استخدام الصيغة التربيعية العائد t = 3.79 ثانية و t = 0.54 ثانية، نظرًا لأن الكرة على ارتفاع 10 أمتار مرتين خلال مسارها - مرة واحدة في الطريق لأعلى ومرة في الطريق إلى الأسفل - نأخذ الحل الأطول للوقت الذي تستغرقه الكرة للوصول إلى المتفرج: $t = 3.79\; s\ lDotP$$يتم تحديد وقت حركة المقذوف تمامًا من خلال الحركة الرأسية. وبالتالي، فإن أي مقذوف تبلغ سرعته الرأسية الأولية 21.2 متر/ثانية ويهبط على ارتفاع 10.0 متر فوق ارتفاعه الأولي يقضي 3.79 ثانية في الهواء.
2. يمكننا العثور على السرعات الأفقية والعمودية النهائية v _x و v _y باستخدام النتيجة من (a). ثم يمكننا الجمع بينهما لإيجاد حجم متجه\(\vec{v}\) السرعة الكلي والزاوية التي\(\theta\) يصنعها مع الأفقي. نظرًا لأن v _x ثابت، يمكننا حله في أي موقع أفقي. نختار نقطة البداية لأننا نعرف السرعة الأولية والزاوية الأولية. لذلك، $$v_ {x} = v_ {0}\ cos\ theta_ {0} = (30\؛ م/ث)\ cos 45^ {o} = 21.2\؛ م/ث\ ldoTP$تُعطى السرعة الرأسية النهائية بالمعادلة\ المرجع {4.21}: $v_ {y} = v_ {0y} − gt\ lDotP$$منذ\(v_{0y}\) أن وجد في الجزء (أ) ليكون 21.2 م/ث، لدينا $v_ {y} = 21.2\؛ م/ث - (9.8\؛ م/ثانية ^ {2}) (3.79 ثانية) = −15.9\؛ م/ث\ ldotp$$ حجم السرعة النهائية\(\vec{v}\) هو $$v =\ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}} =\ sqrt {(21.2\؛ م/ث) ^ {2} + (-15.9\؛ م/ث) ^ {2}} = 26.5\؛ م/ث\ lDotP$تم العثور على الاتجاه\(\theta_{v}\) باستخدام الظل العكسي: $$\ theta_ {v}\ tan^ {-1}\ يسار (\ dfrac {v_ {y}} {v_ {x}}\ يمين) =\ tan^ {-1}\ يسار (\ dfrac {21.2} {-15.9}\ يمين) = -53.1^ {o}\ ldotp$$

الدلالة

1. كما ذكرنا سابقًا، يتم تحديد وقت حركة المقذوفات بالكامل من خلال الحركة الرأسية. وبالتالي، فإن أي مقذوف تبلغ سرعته الرأسية الأولية 21.2 متر/ثانية ويهبط على ارتفاع 10.0 متر فوق ارتفاعه الأولي يقضي 3.79 ثانية في الهواء.
2. تعني الزاوية السالبة أن السرعة هي 53.1 درجة تحت الأفقي عند نقطة التأثير. تتوافق هذه النتيجة مع حقيقة أن الكرة تصطدم عند نقطة على الجانب الآخر من قمة المسار وبالتالي تحتوي على مكون y سالب للسرعة. حجم السرعة أقل من حجم السرعة الأولية التي نتوقعها لأنها تؤثر على 10.0 متر فوق ارتفاع الإطلاق.

وقت الرحلة والمسار والمدى

من الأمور المثيرة للاهتمام وقت الطيران والمسار والمدى لقذيفة تُطلق على سطح أفقي مسطح وتؤثر على نفس السطح. في هذه الحالة، تعطي المعادلات الحركية تعبيرات مفيدة لهذه الكميات، والتي يتم اشتقاقها في الأقسام التالية.

وقت الرحلة

يمكننا حل وقت تحليق المقذوف الذي تم إطلاقه وتأثيره على سطح أفقي مسطح من خلال إجراء بعض التلاعبات في المعادلات الحركية. نلاحظ أن الموضع والإزاحة في y يجب أن يكونا صفرًا عند الإطلاق وعند التأثير على سطح متساوٍ. وبالتالي، نضع الإزاحة في y مساوية للصفر ونجد

\[y − y_{0} = v_{0y} t − \frac{1}{2} gt^{2} = (v_{0} \sin \theta_{0})t − \frac{1}{2} gt^{2} = 0 \ldotp\]

التخصيم، لدينا

\[t \left(v_{0} \sin \theta_{0} - \dfrac{gt}{2}\right) = 0 \ldotp\]

يمنحنا حل المشكلة

\[T_{tof} = \frac{2(v_{0} \sin \theta_{0})}{g} \ldotp \label{4.24}\]

هذا هو وقت الطيران لقذيفة يتم إطلاقها والتأثير على سطح أفقي مسطح. لا تنطبق المعادلة\ ref {4.24} عندما تهبط القذيفة على ارتفاع مختلف عن تلك التي تم إطلاقها، كما رأينا في المثال 4.8 للاعب التنس وهو يضرب الكرة في المدرجات. الحل الآخر، t = 0، يتوافق مع الوقت عند الإطلاق. يتناسب وقت الطيران خطيًا مع السرعة الأولية في اتجاه y ويتناسب عكسيًا مع g، وبالتالي، على القمر، حيث تبلغ الجاذبية سدس جاذبية الأرض، فإن المقذوف الذي يتم إطلاقه بنفس السرعة الموجودة على الأرض سيُنقل جواً ست مرات.

المسار

يمكن العثور على مسار المقذوف عن طريق إزالة المتغير الزمني t من المعادلات الحركية لـ t التعسفي وحل y (x). نأخذ x ₀ = y ₀ = 0 حتى يتم إطلاق المقذوف من الأصل. تعطي المعادلة الكينماتيكية لـ x

\[x = v_{0x}t \Rightarrow t = \frac{x}{v_{0x}} = \frac{x}{v_{0} \cos \theta_{0}} \ldotp\]

استبدال التعبير عن t في معادلة الموضع y = (v ₀ sin\(\theta_{0}\)) t −\(\frac{1}{2}\) gt ² يعطي

\[y = (v_{0} \sin \theta_{0}) \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right) - \frac{1}{2} g \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right)^{2} \ldotp\]

إعادة ترتيب الشروط، لدينا

\[y = (\tan \theta_{0})x - \Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big] x^{2} \ldotp \label{4.25}\]

معادلة المسار هذه من الشكل y = ax + bx ²، وهي معادلة القطع المكافئ مع المعاملات

\[a = \tan \theta_{0}, \quad b = - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \ldotp\]

النطاق

من معادلة المسار يمكننا أيضًا العثور على النطاق أو المسافة الأفقية التي يقطعها المقذوف. معادلة التخصيم\ المرجع {4.25}، لدينا

\[y = x \Big[ \tan \theta_{0} - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} x \Big] \ldotp\]

الموضع y هو صفر لكل من نقطة الإطلاق ونقطة التأثير، نظرًا لأننا نفكر مرة أخرى في سطح أفقي مسطح فقط. يعطي إعداد y = 0 في هذه المعادلة الحلول x = 0، المقابلة لنقطة الإطلاق، و

\[x = \frac{2 v_{0}^{2} \sin \theta_{0} \cos \theta_{0}}{g} ,\]

المقابلة لنقطة التأثير. باستخدام الهوية المثلثية 2sin\(\theta\) cos\(\theta\) = sin2\(\theta\) وإعداد x = R للنطاق، نجد

\[R = \frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \ldotp \label{4.26}\]

لاحظ بشكل خاص أن المعادلة\ ref {4.26} صالحة فقط للإطلاق والتأثير على سطح أفقي. نرى أن النطاق يتناسب طرديًا مع مربع السرعة الأولية v ₀ و sin ²\(\theta_{0}\)، ويتناسب عكسيًا مع تسارع الجاذبية. وبالتالي، على القمر، سيكون النطاق أكبر بست مرات من الأرض لنفس السرعة الأولية. علاوة على ذلك، نرى من عامل sin ²\(\theta_{0}\) أن النطاق هو الحد الأقصى عند 45 درجة. تظهر هذه النتائج في الشكل\(\PageIndex{5}\). في (أ) نرى أنه كلما زادت السرعة الأولية، زاد النطاق. في (b)، نرى أن النطاق هو الحد الأقصى عند 45 درجة. هذا صحيح فقط في الظروف التي تهمل مقاومة الهواء. إذا تم أخذ مقاومة الهواء في الاعتبار، تكون الزاوية القصوى أصغر إلى حد ما. من المثير للاهتمام أنه تم العثور على نفس النطاق لزوايا الإطلاق الأولية التي يبلغ مجموعها 90 درجة. القذيفة التي تم إطلاقها بزاوية أصغر لها قمة أقل من الزاوية الأعلى، لكن كلاهما لهما نفس النطاق.

الشكل\(\PageIndex{5}\): مسارات المقذوفات على مستوى الأرض. (أ) كلما زادت السرعة الأولية v ₀، زاد نطاق زاوية أولية معينة. (ب) تأثير الزاوية الأولية (\ theta_ {0}\) على مدى قذيفة ذات سرعة أولية معينة. لاحظ أن النطاق هو نفسه للزوايا الأولية التي تبلغ 15 درجة و75 درجة، على الرغم من اختلاف الارتفاعات القصوى لهذه المسارات.

مثال 4.9: مقارنة لقطات الجولف

يجد لاعب الجولف نفسه في حالتين مختلفتين في ثقوب مختلفة. في الحفرة الثانية، يقع على بعد 120 مترًا من المنطقة الخضراء ويريد ضرب الكرة 90 مترًا والسماح لها بالركض على المنطقة الخضراء. يقوم بتقريب اللقطة إلى الأرض بزاوية 30 درجة إلى الأفقي للسماح للكرة بالتدحرج بعد الارتطام. في الحفرة الرابعة، يقع على بعد 90 مترًا من المنطقة الخضراء ويريد ترك الكرة تسقط بأقل قدر من التدحرج بعد الاصطدام. وهنا، يقوم بتوجيه اللقطة بزاوية 70 درجة إلى الزاوية الأفقية لتقليل التدحرج بعد الارتطام. يتم ضرب كلتا الطلقتين والتأثير على سطح مستوٍ. (أ) ما السرعة الأولية للكرة عند الثقب الثاني؟ (ب) ما السرعة الأولية للكرة عند الثقب الرابع؟ (ج) اكتب معادلة المسار لكلتا الحالتين. (د) رسم المسارات.

إستراتيجية

نرى أن معادلة النطاق لها السرعة الأولية والزاوية، لذا يمكننا حل السرعة الأولية لكل من (أ) و (ب). عندما نحصل على السرعة الأولية، يمكننا استخدام هذه القيمة لكتابة معادلة المسار.

الحل

1. $R =\ frac {v_ {0} ^ {2}\ الخطيئة 2\ theta_ {0}} {g}\ السهم الأيمن v_ {0} =\ sqrt {\ dfrac {\ dfrac {Rg} {\ sin 2\ theta_ {0}} =\ sqrt {\ dfrac {(90.0\؛ م) (9.8\؛ م/s^ {2}})\ الخطيئة (2 (30^ {o}))}} = 31.9\؛ م/ثانية$$
2. $R =\ frac {v_ {0} ^ {2}\ الخطيئة 2\ theta_ {0}} {g}\ السهم الأيمن v_ {0} =\ sqrt {\ dfrac {\ dfrac {Rg} {\ sin 2\ theta_ {0}} =\ sqrt {\ dfrac {(90.0\؛ م) (9.8\؛ م/s^ {2}})\ الخطيئة (2 (70^ {o}))}} = 37.0\؛ م/ثانية$$
3. $y = x\ كبير [\ تان\ theta_ {0} -\ frac {g} {2 (v_ {0}\ cos\ theta_ {0}) ^ {2}} x\ كبير] $الثقب الثاني: $$y = x\ كبير [\ تان 30^ {o} -\ frac {9.8\; m/s; /s^ {2} {2 [(31.9\; م/ثانية) (التكلفة 30^ {o})] ^ {2} x\ كبير] = 0.58x - 0.0064x^ {2} $$الثقب الرابع: $y = x\ كبير [\ تان 70^ {o} -\ فراك {9.8\; م/s^ {2}} {2} {2} {2} {2} [(37.0\ م/ث) (\ كوس 70^ {o})] ^ {2} x\ كبير] = 2 .75x - 0.0306 × ^ {2} $$
4. باستخدام أداة الرسم البياني، يمكننا مقارنة المسارين الموضحين في الشكل\(\PageIndex{6}\).

الشكل\(\PageIndex{6}\): مساران لكرة الجولف بمدى 90 مترًا، وتكون نقاط الارتطام لكليهما في نفس مستوى نقطة الإطلاق.

الدلالة

السرعة الأولية للتصوير عند 70 درجة أكبر من السرعة الأولية للتصوير عند 30 درجة. لاحظ من الشكل\(\PageIndex{6}\) أن القذيفة التي تم إطلاقها بنفس السرعة ولكن بزوايا مختلفة لهما نفس النطاق إذا كانت زوايا الإطلاق تساوي 90 درجة. يتم إضافة زوايا الإطلاق في هذا المثال لإعطاء رقم أكبر من 90 درجة. وبالتالي، يجب أن تتمتع اللقطة عند 70 درجة بسرعة إطلاق أكبر لتصل إلى 90 مترًا، وإلا فإنها ستهبط على مسافة أقصر.

التمرين 4.4

إذا تم إطلاق رصاصتي الجولف في المثال 4.9 بنفس السرعة، فما الطلقة التي سيكون لها النطاق الأكبر؟

عندما نتحدث عن مدى القذيفة على مستوى الأرض، نفترض أن R صغير جدًا مقارنة بمحيط الأرض. ومع ذلك، إذا كان النطاق كبيرًا، فإن الأرض تنحني بعيدًا تحت المقذوف ويؤدي التسارع الناتج عن الجاذبية إلى تغيير الاتجاه على طول المسار. النطاق أكبر مما توقعته معادلة النطاق المعطاة سابقًا لأن القذيفة ستسقط أكثر مما ستسقط على أرض مستوية، كما هو موضح في الشكل\(\PageIndex{7}\)، الذي يستند إلى رسم في مبدأ نيوتن. إذا كانت السرعة الأولية كبيرة بما يكفي، ينتقل المقذوف إلى المدار. ينخفض سطح الأرض بمقدار 5 أمتار كل 8000 متر، وفي ثانية واحدة يسقط الجسم مسافة 5 أمتار دون مقاومة الهواء. وبالتالي، إذا أُعطي جسم ما سرعة أفقية قدرها 8000 متر/ثانية (أو 18000 ميل/ساعة) بالقرب من سطح الأرض، فسوف يدخل في مدار حول الكوكب لأن السطح يسقط باستمرار بعيدًا عن الجسم. هذه هي تقريبًا سرعة مكوك الفضاء في مدار أرضي منخفض عندما كان يعمل، أو أي قمر صناعي في مدار أرضي منخفض. يتم تغطية هذه الجوانب وغيرها من جوانب الحركة المدارية، مثل دوران الأرض، بعمق أكبر في الجاذبية.

الشكل\(\PageIndex{7}\): قذيفة إلى قمر صناعي. في كل حالة موضحة هنا، يتم إطلاق قذيفة من برج مرتفع جدًا لتجنب مقاومة الهواء. مع زيادة السرعة الأولية، يزداد النطاق ويصبح أطول مما سيكون عليه على الأرض المستوية لأن الأرض تنحني بعيدًا تحت مسارها. يتم تحقيق المدار بسرعة 8000 متر/ثانية.

محاكاة

في PhET Explorations: حركة المقذوفات، تعرف على حركة المقذوفات من حيث زاوية الإطلاق والسرعة الأولية.