2.5: أنظمة الإحداثيات ومكونات المتجه (الجزء 2)
- Page ID
- 199876
الإحداثيات القطبية
لوصف مواقع النقاط أو المتجهات في المستوى، نحتاج إلى اتجاهين متعامدين. في نظام الإحداثيات الديكارتية، تُعطى هذه الاتجاهات بواسطة متجهات الوحدة\(\hat{i}\) وعلى\(\hat{j}\) طول المحور السيني والمحور y، على التوالي. يعد نظام الإحداثيات الديكارتية مناسبًا جدًا للاستخدام في وصف عمليات النزوح وسرعات الأجسام والقوى المؤثرة عليها. ومع ذلك، يصبح الأمر مرهقًا عندما نحتاج إلى وصف دوران الكائنات. عند وصف الدوران، نعمل عادةً في نظام الإحداثيات القطبية.
في نظام الإحداثيات القطبية، يتم تحديد موقع النقطة P في المستوى من خلال إحداثيتين قطبيتين (الشكل\(\PageIndex{1}\)). الإحداثيات القطبية الأولى هي الإحداثيات الشعاعية r، وهي مسافة النقطة P من الأصل. الإحداثيات القطبية الثانية هي زاوية\(\varphi\) يصنعها المتجه الشعاعي مع بعض الاتجاهات المختارة، وعادة ما يكون الاتجاه x الموجب. في الإحداثيات القطبية، يتم قياس الزوايا بالراديان أو الدرجات. يتم توصيل المتجه الشعاعي عند نقطة الأصل ويشير بعيدًا عن نقطة الأصل إلى النقطة P. يتم وصف هذا الاتجاه الشعاعي بواسطة متجه شعاعي للوحدة\(\hat{r}\). متجه الوحدة الثانية\(\hat{t}\) هو ناقل متعامد للاتجاه الشعاعي\(\hat{r}\). يشير\(\hat{t}\) الاتجاه الموجب + إلى كيفية\(\varphi\) تغير الزاوية في اتجاه عكس اتجاه عقارب الساعة. بهذه الطريقة، يمكن وصف النقطة P التي تحتوي على إحداثيات (x، y) في النظام المستطيل بشكل مكافئ في نظام الإحداثيات القطبية بواسطة الإحداثيين القطبيين (r،\(\varphi\)). المعادلة 2.4.13 صالحة لأي متجه، لذا يمكننا استخدامها للتعبير عن إحداثيات x و y للمتجه\(\vec{r}\). بهذه الطريقة نحصل على الاتصال بين الإحداثيات القطبية والإحداثيات المستطيلة للنقطة P:
\[ \begin{cases} x = r \cos \varphi \\ y = r \sin \varphi \end{cases} \ldotp \label{2.18}\]
يعثر أحد الباحثين عن الكنوز على عملة فضية واحدة في موقع يبعد 20.0 مترًا عن بئر جاف في اتجاه 20 درجة شمال الشرق ويجد عملة ذهبية واحدة في موقع يبعد 10.0 مترًا عن البئر في اتجاه 20 درجة شمال الغرب. ما الإحداثيات القطبية والمستطيلة لهذه النتائج بالنسبة للبئر؟
إستراتيجية
يمثل البئر أصل نظام الإحداثيات والشرق هو اتجاه +x. نحدد المسافات الشعاعية من المواقع إلى الأصل، وهي r S = 20.0 m (للعملة الفضية) و r G = 10.0 m (للعملة الذهبية). للعثور على الإحداثيات الزاوية، نقوم بتحويل 20 درجة إلى راديان: 20° =\(\frac{\pi\; 20}{180}\) =\(\frac{\pi}{9}\). نستخدم المعادلة\ ref {2.18} للعثور على إحداثيات x- و y للعملات.
الحل
الإحداثيات الزاوية للعملة الفضية هي\(\varphi_{S}\) =\(\frac{\pi}{9}\)، في حين أن الإحداثيات الزاوية للعملة الذهبية هي\(\varphi_{G}\) =\(\pi\) −\(\frac{\pi}{9}\) =\(\frac{8 \pi}{9}\). وبالتالي، فإن الإحداثيات القطبية للعملة الفضية هي (r S،\(\varphi_{S}\)) = (20.0 m،\(\frac{\pi}{9}\)) وتلك الخاصة بالعملة الذهبية هي (r G،\(\varphi_{G}\)) = (10.0 m،\ frac {8\ pi} {9}\)). نستبدل هذه الإحداثيات بالمعادلة\ ref {2.18} للحصول على إحداثيات مستطيلة. بالنسبة للعملة الذهبية، الإحداثيات هي
\[ \begin{cases} x_{G} = r_{G} \cos \varphi_{G} = (10.0\; m) \cos \frac{8 \pi}{9} = -9.4\; m \\ y_{G} = r_{G} \sin \varphi_{G} = (10.0\; m) \sin \frac{8 \pi}{9} = 3.4\; m \end{cases} \Rightarrow (x_{G}, y_{G}) = (-9.4\; m, 3.4\; m) \ldotp\]
بالنسبة للعملة الفضية، الإحداثيات هي
\[ \begin{cases} x_{S} = r_{S} \cos \varphi_{S} = (20.0\; m) \cos \frac{\pi}{9} = 18.9\; m \\ y_{S} = r_{S} \sin \varphi_{S} = (20.0\; m) \sin \frac{\pi}{9} = 6.8\; m \end{cases} \Rightarrow (x_{S}, y_{S}) = (18.9\; m, 6.8\; m) \ldotp\]
المتجهات في ثلاثة أبعاد
لتحديد موقع نقطة في الفضاء، نحتاج إلى ثلاثة إحداثيات (x، y، z)، حيث تحدد الإحداثيات x و y المواقع في الطائرة، والإحداثيات z تعطي المواضع الرأسية فوق المستوى أو أسفله. يحتوي الفضاء ثلاثي الأبعاد على ثلاثة اتجاهات متعامدة، لذلك لا نحتاج إلى متجه وحدتين بل ثلاث وحدات لتعريف نظام الإحداثيات ثلاثي الأبعاد. في نظام الإحداثيات الديكارتية، يكون أول متجه للوحدة هو متجه الوحدة للمحور السيني\(\hat{i}\) ومتجه الوحدة للمحور y\(\hat{j}\). متجه الوحدة الثالثة\(\hat{k}\) هو اتجاه المحور z (الشكل\(\PageIndex{2}\)). يعتبر الترتيب الذي يتم به تسمية المحاور، وهو الترتيب الذي تظهر به متجهات الوحدات الثلاث، مهمًا لأنه يحدد اتجاه نظام الإحداثيات. يحدد الترتيب x-y-z، الذي يعادل الترتيب\(\hat{i}\) -\(\hat{j}\) -\(\hat{k}\)، نظام الإحداثيات القياسي لليد اليمنى (الاتجاه الإيجابي).
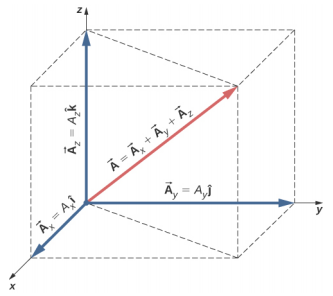
في الفضاء ثلاثي الأبعاد،\(\vec{A}\) يحتوي المتجه على ثلاثة مكونات متجهة: المكون x\(\vec{A}_{x}\) = A x\(\hat{i}\)، وهو جزء من المتجه\(\vec{A}\) على طول المحور x؛ المكون y\(\vec{A}_{y}\) = A y\(\hat{j}\)، وهو جزء من\(\vec{A}\) على طول y- المحور؛ والمكون z\(\vec{A}_{z}\) = A z\(\hat{k}\)، وهو جزء من المتجه على طول المحور z. المتجه في الفضاء ثلاثي الأبعاد هو المجموع المتجه لمكوناته المتجهية الثلاثة (الشكل\(\PageIndex{3}\)):
\[\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k} \ldotp \label{2.19}\]
إذا عرفنا إحداثيات أصله ب (x b، y b، z b) ونهايته e (x e y e، z e)، يتم الحصول على مكوناته العددية بأخذ اختلافاتها: يتم إعطاء A x و A y بواسطة
\[ \begin{cases} A_{x} = x_{e} - x_{b} \nonumber \\ A_{y} = y_{e} - y_{b} \ldotp \nonumber \end{cases} \]
ويتم إعطاء المكون z بواسطة
\[A_{z} = z_{e} - z_{b} \ldotp \label{2.20}\]
يتم الحصول على المقدار A من خلال تعميم المعادلة 2.4.8 إلى ثلاثة أبعاد:
\[A = \sqrt{A_{x}^{2} + A_{y}^{2} + A_{z}^{2}} \ldotp \label{2.21}\]
يأتي هذا التعبير عن حجم المتجه من تطبيق نظرية فيثاغورس مرتين. كما هو موضح في الشكل\(\PageIndex{3}\)، فإن القطر في المستوى y له طول\(\sqrt{A_{x}^{2} + A_{y}^{2}}\) ويضيف مربعه إلى المربع A z 2 لإعطاء A 2. لاحظ أنه عندما يكون المكون z صفرًا، فإن المتجه يقع بالكامل في المستوى xy ويتم تقليل وصفه إلى بعدين.
أثناء إقلاع طائرة IAI Heron (الشكل\(\PageIndex{4}\))، يكون موقعها فيما يتعلق ببرج المراقبة 100 متر فوق سطح الأرض، و300 متر إلى الشرق، و200 متر إلى الشمال. بعد دقيقة واحدة، أصبح موقعها على ارتفاع 250 مترًا فوق سطح الأرض، و 1200 مترًا إلى الشرق، و 2100 مترًا إلى الشمال. ما هو ناقل الإزاحة للطائرة بدون طيار فيما يتعلق ببرج المراقبة؟ ما مقدار متجه الإزاحة؟
إستراتيجية
نحن نأخذ أصل نظام الإحداثيات الديكارتية كبرج مراقبة. يتم إعطاء اتجاه المحور +x بواسطة متجه الوحدة\(\hat{i}\) إلى الشرق، ويتم إعطاء اتجاه المحور +y بواسطة متجه الوحدة\(\hat{j}\) إلى الشمال، ويتم إعطاء اتجاه المحور +z بواسطة متجه الوحدة\(\hat{k}\)، الذي يشير لأعلى من الأرض. الموضع الأول للطائرة بدون طيار هو أصل (أو، على نحو مماثل، البداية) لناقل الإزاحة وموضعه الثاني هو نهاية ناقل الإزاحة.
الحل
نحدد b (300.0 م، 200.0 م، 100.0 م) و e (480.0 م، 370.0 م، 250.0 م)، ونستخدم المعادلة 2.4.4 والمعادلة\ المرجع {2.20} للعثور على المكونات العددية لمتجه الإزاحة للطائرة بدون طيار:
\[ \begin{cases} D_{x} = x_{e} - x_{b} = 1200.0\; m - 300.0\; m = 900.0\; m,\\ D_{y} =y_{e} - y_{b} = 2100.0\; m - 200.0\; m = 1900.0\; m, \\ D_{z} =z_{e} - z_{b} = 250.0\; m - 100.0\; m = 150\; m \ldotp \end{cases}\]
نستبدل هذه المكونات في المعادلة\ ref {2.19} للعثور على متجه الإزاحة:
\[\vec{D} = D_{x}\; \hat{i} + D_{y}\; \hat{j} + D_{z}\; \hat{k} = 900.0\; \hat{i} + 1900.0\; \hat{j} + 150.0\; \hat{k} = (0.90\; \hat{i} + 1.90\; \hat{j} + 0.15\; \hat{k})\; km \ldotp\]
نستبدل المعادلة\ ref {2.21} للعثور على حجم الإزاحة:
\[D = \sqrt{D_{x}^{2} + D_{y}^{2} + D_{z}^{2}} = \sqrt{(0.90\; km)^{2} + (1.90\; km)^{2} + (0.15\; km)^{2}} = 4.44\; km \ldotp\]
إذا كان متوسط متجه السرعة للطائرة بدون طيار في الإزاحة في المثال 2.7 هو\(\vec{u}\) = (15.0\(\hat{i}\)\(\hat{j}\) + 31.7 + 2.5\(\hat{k}\)) م/ث، فما مقدار متجه سرعة الطائرة بدون طيار؟


