Skip to main content
Global

2.3: الأرقام القياسية والمتجهات (الجزء 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    199889

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    مثال\(\PageIndex{1}\): A Ladybug Walker

    توجد عصا قياس طويلة على الحائط في مختبر الفيزياء بطرف يبلغ طوله 200 سم على الأرض. تهبط الخنفساء على علامة 100 سم وتزحف عشوائيًا على طول العصا. يمشي أولاً 15 سم باتجاه الأرض، ثم يمشي 56 سم باتجاه الحائط، ثم يمشي 3 سم باتجاه الأرض مرة أخرى. ثم، بعد توقف قصير، يستمر لمدة 25 سم باتجاه الأرض، ثم يزحف مرة أخرى لمسافة 19 سم باتجاه الحائط قبل أن يستريح تمامًا (الشكل\(\PageIndex{1}\)). أوجد متجه الإزاحة الكلية وموضع ثباته الأخير على العصا.

    إستراتيجية

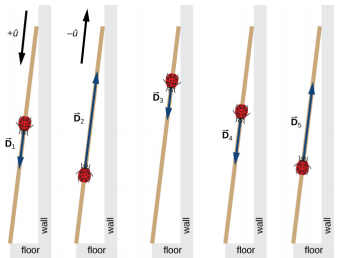
    إذا اخترنا الاتجاه على طول العصا باتجاه الأرض كاتجاه متجه الوحدة\(\hat{u}\)، فإن الاتجاه نحو الأرض هو\(+ \hat{u}\) والاتجاه نحو الجدار هو\(−\hat{u}\). تقوم الخنفساء بما مجموعه خمس عمليات نزوح:

    \[ \begin{align*} \vec{D}_{1} &= (15\; cm)( + \hat{u}), \\[4pt] \vec{D}_{2} &= (56\; cm)( - \hat{u}), \\[4pt] \vec{D}_{3} &= (3\; cm)( + \hat{u}), \\[4pt] \vec{D}_{4} &= (25\; cm)( + \hat{u}), \; and \\[4pt] \vec{D}_{5} &= (19\; cm)( - \hat{u}) \ldotp \end{align*}\]

    الإزاحة الكلية\(\vec{D}\) هي نتيجة جميع ناقلات الإزاحة الخاصة بها.

    خمسة رسوم توضيحية لخنفساء على مسطرة تتكئ على الحائط. يكون اتجاه القبعة +u نحو الأرضية الموازية للمسطرة، واتجاه القبعة - u هو الأعلى على طول المسطرة. في الرسم التوضيحي الأول، توجد الخنفساء بالقرب من منتصف المسطرة ويشير المتجه D الفرعي 1 إلى أسفل المسطرة. في الرسم التوضيحي الثاني، تقع الخنفساء في الأسفل، حيث يوجد رأس المتجه D sub 1 في الرسم التوضيحي الأول، ويشير المتجه D الفرعي 2 إلى أعلى المسطرة. في الرسم التوضيحي الثالث، تقع الخنفساء في أعلى، حيث يوجد رأس المتجه D sub 2 في الرسم التوضيحي الثاني، ويشير المتجه D الفرعي 3 إلى أسفل المسطرة. في الرسم التوضيحي الرابع، توجد الخنفساء في الأسفل، حيث يوجد رأس المتجه D sub 3 في الرسم التوضيحي الثالث، ويشير المتجه D الفرعي 4 إلى أسفل المسطرة. في الرسم التوضيحي الخامس، توجد الخنفساء في الأسفل، حيث يوجد رأس المتجه D sub 4 في الرسم التوضيحي الرابع، ويشير المتجه D الفرعي 5 إلى أعلى المسطرة.
    الشكل\(\PageIndex{1}\): خمس عمليات نزوح للخنفساء. لاحظ أنه في هذا الرسم التخطيطي، لا يتم رسم مقادير النزوح على نطاق واسع. (مصدر: تعديل عمل لـ «الشاعر الفارسي غال» /ويكيميديا كومنز)
    الحل

    محصلة جميع ناقلات الإزاحة هي

    \[ \begin{align*} \vec{D} &= \vec{D}_{1} + \vec{D}_{2} + \vec{D}_{3} + \vec{D}_{4} + \vec{D}_{5} \\[4pt] &= (15\; cm)( + \hat{u} ) + (56\; cm)( −\hat{u} ) + (3\; cm)( + \hat{u} ) + (25\; cm)( + \hat{u}) + (19\; cm)( − \hat{u}) \\[4pt] &= (15 − 56 + 3 + 25 − 19) cm\; \hat{u} \\[4pt] &= −32\; cm\; \hat{u} \ldotp \end{align*}\]

    في هذا الحساب، نستخدم قانون التوزيع المعطى بالمعادلة 2.2.9. تشير النتيجة إلى أن متجه الإزاحة الكلي يشير بعيدًا عن علامة 100 سم (موقع الهبوط الأولي) باتجاه نهاية عصا العداد التي تلامس الجدار. تم تحديد الطرف الذي يلامس الجدار بـ 0 سم، وبالتالي فإن الموضع النهائي للخنفساء يكون عند علامة (100 - 32) سم = 68 سم.

    التمرين 2.2

    غواص الكهف يدخل نفقًا طويلًا تحت الماء. عندما تبلغ المسافة التي قطعتها عن نقطة الدخول 20 مترًا، فإنها تسقط كاميرتها عن طريق الخطأ، لكنها لا تلاحظ فقدها حتى تبتعد عن النفق بحوالي 6 أمتار. تسبح لمسافة 10 أمتار ولكنها لا تستطيع العثور على الكاميرا، لذلك قررت إنهاء الغوص. كم تبعد عن نقطة الدخول؟ عند أخذ الاتجاه الموجب للخروج من النفق، ما هو متجه الإزاحة الخاص بها بالنسبة إلى نقطة الدخول؟

    جبر المتجهات في بعدين

    عندما تكمن المتجهات في مستوى - أي عندما تكون في بعدين - يمكن ضربها بالأرقام القياسية أو إضافتها إلى متجهات أخرى أو طرحها من متجهات أخرى وفقًا للقوانين العامة المعبر عنها في المعادلة 2.2.1، المعادلة 2.. 2.2، المعادلة 2.2.7، و المعادلة 2.2.8. ومع ذلك، تصبح قاعدة الجمع لمتجهين في المستوى أكثر تعقيدًا من قاعدة إضافة المتجهات في بُعد واحد. علينا استخدام قوانين الهندسة لإنشاء المتجهات الناتجة، متبوعًا بعلم المثلثات للعثور على مقادير المتجهات والاتجاهات. يشيع استخدام هذا الأسلوب الهندسي في التنقل (الشكل\(\PageIndex{2}\)). في هذا القسم، نحتاج إلى أن يكون لدينا مساطر، ومثلث، ومنقلة، وقلم رصاص، وممحاة لرسم المتجهات لتوسيع نطاقها من خلال الإنشاءات الهندسية.

    صورة لشخص يقيس المسافة على الخريطة باستخدام الفرجار والمسطرة.
    الشكل\(\PageIndex{2}\): في الملاحة، تُستخدم قوانين الهندسة لرسم الإزاحات الناتجة على الخرائط البحرية.

    للحصول على بناء هندسي لمجموع متجهين في المستوى، نتبع قاعدة متوازي الأضلاع. لنفترض وجود متجهين\(\vec{A}\)\(\vec{B}\) وهما في المواضع التعسفية الموضحة في الشكل\(\PageIndex{3}\). ترجم أيًا منهما بالتوازي مع بداية المتجه الآخر، بحيث تكون أصول كلا المتجهين في نفس النقطة بعد الترجمة. الآن، في نهاية المتجه،\(\vec{A}\) نرسم خطًا موازيًا للمتجه\(\vec{B}\) وفي نهاية المتجه\(\vec{B}\) نرسم خطًا موازيًا للمتجه\(\vec{A}\) (الخطوط المتقطعة في الشكل\(\PageIndex{3}\)). بهذه الطريقة نحصل على متوازي الأضلاع. من أصل المتجهين نرسم قطرًا هو ناتج\(\vec{R}\) المتجهين:\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) (الشكل\(\PageIndex{3a}\)). القطر الآخر لهذا متوازي الأضلاع هو الفرق المتجه للمتجهين\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\)، كما هو موضح في الشكل\(\PageIndex{3b}\). لاحظ أن نهاية متجه الفرق يتم وضعها في نهاية المتجه\(\vec{A}\).

    تم توضيح طريقة متوازي الأضلاع لإضافة المتجهات. في الشكل أ، يتم عرض المتجهين A و B. يشير المتجه A إلى اليمين والأسفل ويشير المتجه B إلى اليمين وإلى الأعلى. ثم يتم عرض المتجهين A و B كسهام صلبة مع ذيولها معًا واتجاهاتها كما كان من قبل. يظهر خط متقطع موازٍ للمتجه A ولكنه تم تحريكه بحيث يبدأ عند رأس B. يظهر أيضًا الخط المتقطع الثاني الموازي لـ B ويبدأ من رأس A. يشكل المتجهان A و B والخطان المتقطعان متوازي الأضلاع. يظهر متجه ثالث، يسمى المتجه R = المتجه A بالإضافة إلى المتجه B. يقع ذيل المتجه R في ذيول المتجهين A و B، ورأس المتجه R هو المكان الذي تلتقي فيه الخطوط المتقطعة ببعضها البعض، قطريًا عبر متوازي الأضلاع. نلاحظ أن حجم R لا يساوي حجم A زائد حجم B. في الشكل b، يتم عرض المتجهين A و B. المتجه ناقص B هو المتجه B من الجزء أ، ويتم تدويره بمقدار 180 درجة. يشير المتجه A إلى اليمين والأسفل والمتجه ناقص نقاط B إلى اليسار وإلى الأسفل. ثم يتم عرض المتجهين A و B كسهام صلبة مع ذيولها معًا واتجاهاتها كما كان من قبل. يظهر خط متقطع موازٍ للمتجه A ولكنه تم تحريكه بحيث يبدأ عند رأس B. يظهر أيضًا الخط المتقطع الثاني الموازي لـ B ويبدأ من رأس A. يشكل المتجهان A و B والخطان المتقطعان متوازي الأضلاع. يظهر متجه ثالث يسمى المتجه D. يقع ذيل المتجه D على رأس المتجه B، ويكون رأس المتجه D على رأس المتجه A، قطريًا عبر متوازي الأضلاع. نلاحظ أن المتجه D يساوي المتجه A ناقص المتجه B، لكن حجم D لا يساوي حجم A ناقص B.
    الشكل\(\PageIndex{3}\): قاعدة متوازي الأضلاع لإضافة متجهين. قم بعمل الترجمة المتوازية لكل متجه إلى نقطة تتطابق فيها أصولها (المميزة بالنقطة) وقم بإنشاء متوازي أضلاع له جانبان على المتجهات والجانبان الآخران (المشار إليهما بخطوط متقطعة) يوازي المتجهات. (أ) ارسم المتجه الناتج\(\vec{R}\) على طول قطر متوازي الأضلاع من النقطة المشتركة إلى الزاوية المقابلة. طول R للمتجه الناتج لا يساوي مجموع مقادير المتجهين. (ب) ارسم متجه الفرق\(\vec{D}\) =\(\vec{A}\) -\(\vec{B}\) على طول القطر الذي يربط طرفي المتجهات. ضع أصل المتجه\(\vec{D}\) في نهاية المتجه\(\vec{B}\) ونهاية (رأس السهم) للمتجه\(\vec{D}\) في نهاية المتجه\(\vec{A}\). الطول D لمتجه الفرق لا يساوي الفرق في مقادير المتجهين.

    ويترتب على قاعدة متوازي الأضلاع أنه لا يمكن التعبير عن حجم المتجه الناتج ولا حجم متجه الفرق كمجموع بسيط أو فرق في المقادير A و B، لأنه لا يمكن التعبير عن طول القطر كمجموع بسيط لأطوال الأضلاع. عند استخدام البناء الهندسي للعثور على المقادير | | و\(\vec{R}\) |\(\vec{D}\) |، علينا استخدام قوانين علم المثلثات للمثلثات، مما قد يؤدي إلى جبر معقد. هناك طريقتان للتحايل على هذا التعقيد الجبري. إحدى الطرق هي استخدام طريقة المكونات التي نفحصها في القسم التالي. والطريقة الأخرى هي رسم المتجهات حسب الحجم، كما هو الحال في الملاحة، وقراءة أطوال المتجهات والزوايا التقريبية (الاتجاهات) من الرسوم البيانية. في هذا القسم ندرس النهج الثاني.

    إذا احتجنا إلى إضافة ثلاثة متجهات أو أكثر، فإننا نكرر قاعدة متوازي الأضلاع لأزواج المتجهات حتى نجد محصلة جميع النتائج. بالنسبة لثلاثة متجهات، على سبيل المثال، نجد أولاً ناتج المتجه 1 والمتجه 2، ثم نجد ناتج هذا الناتج والمتجه 3. لا يهم الترتيب الذي نختار به أزواج المتجهات لأن عملية جمع المتجهات هي عملية تبادلية ورابطية (انظر المعادلة 2.2.7 والمعادلة 2.2.8). قبل أن نذكر قاعدة عامة تنبع من التطبيقات المتكررة لقاعدة متوازي الأضلاع، دعونا ننظر إلى المثال التالي.

    لنفترض أنك تخطط لرحلة عطلة في فلوريدا. عند مغادرتك تالاهاسي، عاصمة الولاية، تخطط لزيارة عمك جو في جاكسونفيل، ورؤية ابن عمك فيني في دايتونا بيتش، والتوقف للحصول على القليل من المرح في أورلاندو، ومشاهدة عرض السيرك في تامبا، وزيارة جامعة فلوريدا في غينزفيل. قد يتم تمثيل مسارك بخمسة متجهات للإزاحة\(\vec{A}\)\(\vec{B}\)\(\vec{C}\)، و\(\vec{D}\)، و\(\vec{E}\)، والتي تشير إليها المتجهات الحمراء في الشكل\(\PageIndex{4}\). ما هو إجمالي نزوحك عندما تصل إلى Gainesville؟ إجمالي الإزاحة هو المجموع المتجه لجميع متجهات الإزاحة الخمسة، والذي يمكن العثور عليه باستخدام قاعدة متوازي الأضلاع أربع مرات. بدلاً من ذلك، تذكر أن متجه الإزاحة له بدايته في الموضع الأولي (تالاهاسي) ونهايته في الموضع النهائي (Gainesville)، لذلك يمكن رسم متجه الإزاحة الكلي مباشرة كسهم يربط تالاهاسي بـ Gainesville (انظر المتجه الأخضر في الشكل\(\PageIndex{4}\)). عندما نستخدم قاعدة متوازي الأضلاع أربع مرات، فإن النتيجة التي\(\vec{R}\) نحصل عليها هي بالضبط هذا المتجه الأخضر الذي يربط تالاهاسي بـ Gainesville:\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\) +\(\vec{E}\).

    خريطة لفلوريدا مع المتجهات التالية موضحة باللون الأحمر: المتجه A من تالاهاسي إلى جاكسونفيل، نحو الغرب تقريبًا. ناقل الحركة B من جاكسونفيل إلى دايتونا بيتش، جنوب شرق البلاد. ناقل الحركة C من دايتونا بيتش إلى أورلاندو، جنوب غرب البلاد. Vector D من أورلاندو إلى تامبا، جنوب غرب البلاد (ولكن أقل رأسيًا من المتجه C). المتجه E من تامبا إلى غينزفيل، إلى الشرق قليلاً من الشمال. يظهر المتجه R من تالاهاسي إلى غينزفيل كسهم أخضر.
    الشكل\(\PageIndex{4}\): عندما نستخدم قاعدة متوازي الأضلاع أربع مرات، نحصل على المتجه الناتج\(\vec{R}\) =\(\vec{A}\) + + +\(\vec{B}\)\(\vec{C}\)\(\vec{D}\) +\(\vec{E}\)، وهو المتجه الأخضر الذي يربط تالاهاسي بـ Gainesville.

    يمكن تعميم رسم المتجه الناتج للعديد من المتجهات باستخدام البناء الهندسي التالي من الذيل إلى الرأس. لنفترض أننا نريد رسم المتجه\(\vec{R}\) الناتج لأربعة متجهات\(\vec{A}\)، و\(\vec{B}\)\(\vec{C}\)، و\(\vec{D}\) (الشكل\(\PageIndex{5a}\)). نختار أيًا من المتجهات باعتباره المتجه الأول ونقوم بترجمة متوازية للمتجه الثاني إلى موضع يتزامن فيه أصل («الذيل») للمتجه الثاني مع نهاية («الرأس») للمتجه الأول. ثم نختار متجهًا ثالثًا ونقوم بترجمة متوازية للمتجه الثالث إلى موضع يتزامن فيه أصل المتجه الثالث مع نهاية المتجه الثاني. نكرر هذا الإجراء حتى تصبح جميع المتجهات في ترتيب من الرأس إلى الذيل مثل الذي يظهر في الشكل\(\PageIndex{5}\). نرسم المتجه الناتج\(\vec{R}\) عن طريق ربط الأصل («الذيل») للمتجه الأول بنهاية («الرأس») للمتجه الأخير. تكون نهاية المتجه الناتج في نهاية المتجه الأخير. نظرًا لأن إضافة المتجهات هي عملية ترابطية وتبديلية، فإننا نحصل على نفس المتجه الناتج بغض النظر عن المتجه الذي نختاره ليكون الأول أو الثاني أو الثالث أو الرابع في هذا البناء.

    في الشكل أ، يتم عرض أربعة متجهات، تسمى A و B و C و D بشكل فردي. في الشكل ب، تظهر المتجهات مرتبة من الرأس إلى الذيل: ذيل المتجه A يقع على رأس D. ذيل المتجه C على رأس A. وذيل المتجه B يقع على رأس C. ويشير كل متجه في نفس الاتجاه كما هو في الشكل a. يبدأ المتجه الخامس، R، عند ذيل المتجه D وينتهي عند رأس ناقل ب.
    الشكل\(\PageIndex{5}\): طريقة الذيل إلى الرأس لرسم المتجه الناتج\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\). (أ) أربعة متجهات بمقادير واتجاهات مختلفة. (ب) تُترجم المتجهات في (أ) إلى مواضع جديدة يكون فيها أصل («ذيل») أحد المتجهات في نهاية («الرأس») لمتجه آخر. يتم رسم المتجه الناتج من أصل («الذيل») للمتجه الأول إلى نهاية («الرأس») للمتجه الأخير في هذا الترتيب.
    مثال\(\PageIndex{2}\): Geometric Construction of the Resultant

    \(\PageIndex{6}\)تُحدَّد متجهات الإزاحة الثلاثة\(\vec{A}\)\(\vec{B}\)،\(\vec{C}\) وفي الشكل، بمقاييسها A = 10.0، B = 7.0، C = 8.0، على التوالي، ومن خلال زوايا الاتجاه الخاصة بكل منها مع الاتجاه الأفقي\(\alpha\) = 35°،\(\beta\) = −110°،\(\gamma\) و= 30°. الوحدات المادية للمقاييس هي سنتيمترات. اختر مقياسًا مناسبًا واستخدم مسطرة ومنقلة للعثور على مجاميع المتجهات التالية: (أ)\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\)، (ب)\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\)، و (ج)\(\vec{S}\) =\(\vec{A}\) −\(3 \vec{B}\) +\(\vec{C}\).

    يبلغ حجم المتجه A 10.0 ويقع بزاوية ألفا = 35 درجة عكس اتجاه عقارب الساعة من الأفقي. يشير إلى الأعلى واليمين. يبلغ حجم المتجه B 7.0 وهو بزاوية بيتا = -110 درجة في اتجاه عقارب الساعة من الأفقي. يشير إلى الأسفل واليسار. يبلغ حجم المتجه C 8.0 وهو بزاوية جاما = 30 درجة عكس اتجاه عقارب الساعة من الأفقي. يشير إلى الأعلى واليمين. يبلغ حجم المتجه F 20.0 وهو بزاوية phi = 110 درجة عكس اتجاه عقارب الساعة من الأفقي. يشير إلى الأعلى واليسار.
    الشكل\(\PageIndex{6}\): المتجهات المستخدمة في المثال\(\PageIndex{2}\) وفي ميزة التمرين التالية.

    إستراتيجية

    في البناء الهندسي، يعني العثور على متجه إيجاد حجمه وزاوية اتجاهه بالاتجاه الأفقي. تتمثل الإستراتيجية في رسم مقياس المتجهات التي تظهر على الجانب الأيمن من المعادلة وبناء المتجه الناتج. ثم استخدم مسطرة ومنقلة لقراءة مقدار الناتج وزاوية الاتجاه. بالنسبة للأجزاء (أ) و (ب) نستخدم قاعدة متوازي الأضلاع. بالنسبة لـ (ج) نستخدم طريقة الذيل إلى الرأس.

    الحل

    بالنسبة للأجزاء (أ) و (ب)، نرفق أصل المتجه\(\vec{B}\) بأصل المتجه\(\vec{A}\)، كما هو موضح في الشكل\(\PageIndex{7}\)، ونبني متوازي الأضلاع. القطر الأقصر لهذا متوازي الأضلاع هو المجموع\(\vec{A}\) +\(\vec{B}\). طول الأقطار هو الفرق\(\vec{A}\) -\(\vec{B}\). نستخدم مسطرة لقياس أطوال الأقطار، ومنقلة لقياس الزوايا بالأفقية. للحصول على النتيجة\(\vec{R}\)، نحصل على R = 5.8 سم و\(\theta_{R}\) ≈ 0 درجة. بالنسبة للفرق\(\vec{D}\)، نحصل على D = 16.2 سم و\(\theta_{D}\) = 49.3 درجة، كما هو موضح في الشكل\(\PageIndex{7}\).

    تظهر ثلاثة مخططات للمتجهين A و B. المتجهين A و B موضوعة من الذيل إلى الذيل. يشير المتجه A لأعلى ولليمين ويبلغ حجمه 10.0. يشير المتجه B إلى الأسفل واليسار ويبلغ حجمه 7.0. الزاوية بين المتجهين A و B هي 145 درجة. في المخطط الثاني، يتم عرض المتجهين A و B مرة أخرى جنبًا إلى جنب مع الخطوط المتقطعة التي تكمل متوازي الأضلاع. يظهر المتجه R الذي يساوي مجموع المتجهين A و B كمتجه من ذيول A و B إلى الرأس المعاكس لمتوازي الأضلاع. حجم R هو 5.8. في المخطط الثالث، يتم عرض المتجهين A و B مرة أخرى جنبًا إلى جنب مع الخطوط المتقطعة التي تكمل متوازي الأضلاع. يظهر المتجه D الذي يساوي الفرق بين المتجهين A و B كمتجه من رأس B إلى رأس A. حجم D هو 16.2، والزاوية بين D والأفقي هي 49.3 درجة. المتجه R في الرسم التخطيطي الثاني أقصر بكثير من المتجه D في الرسم التخطيطي الثالث.
    الشكل\(\PageIndex{7}\): استخدام قاعدة متوازي الأضلاع لحل (أ) (إيجاد الناتج، الأحمر) و (ب) (إيجاد الفرق، الأزرق).

    بالنسبة إلى (c)، يمكننا البدء بالمتجه −3\(\vec{B}\) ورسم المتجهات المتبقية من الذيل إلى الرأس كما هو موضح في الشكل\(\PageIndex{8}\). في جمع المتجهات، يكون الترتيب الذي نرسم به المتجهات غير مهم، ولكن رسم المتجهات للقياس مهم جدًا. بعد ذلك، نرسم المتجه\(\vec{S}\) من أصل المتجه الأول إلى نهاية المتجه الأخير ونضع رأس السهم في نهايته\(\vec{S}\). نستخدم مسطرة لقياس طولها\(\vec{S}\)، ونجد أن حجمها هو S = 36.9 cm. نستخدم منقلة ونجد أن زاوية اتجاهها هي\(\theta_{S}\) = 52.9 درجة. يظهر هذا الحل في الشكل\(\PageIndex{8}\).

    تظهر ثلاثة متجهات باللون الأزرق وتوضع من الرأس إلى الذيل: يشير المتجه ناقص 3 B إلى الأعلى وإلى اليمين ويبلغ حجمه 3 B = 21.0. يبدأ المتجه A عند رأس B، ويشير لأعلى ولليمين، ويكون حجمه A = 10.0. الزاوية بين المتجه A والمتجه ناقص 3 B هي 145 درجة. يبدأ المتجه C عند رأس A ويبلغ حجمه C = 8.0. المتجه S أخضر وينتقل من ذيل ناقص 3 B إلى رأس C. Vector S يساوي المتجه A ناقص 3 المتجه B زائد المتجه C، ويبلغ حجمه S=36.9 ويجعل زاوية 52.9 درجة عكس اتجاه عقارب الساعة مع الأفقي.
    الشكل\(\PageIndex{8}\): استخدام طريقة الذيل إلى الرأس لحل (c) (العثور على المتجه\(\vec{S}\)، الأخضر).
    التمرين 2.3

    باستخدام متجهات الإزاحة الثلاثة\(\vec{A}\)\(\vec{B}\)،\(\vec{F}\) وفي الشكل\(\PageIndex{6}\)، اختر مقياسًا مناسبًا، واستخدم المسطرة والمنقلة لإيجاد المتجه\(\vec{G}\) المعطى بمعادلة المتجهات\(\vec{G}\) =\(\vec{A}\) +\(2 \vec{B}\) −\(\vec{F}\).

    محاكاة

    لاحظ إضافة المتجهات في الطائرة من خلال زيارة حاسبة المتجهات هذه ومحاكاة PhET هذه.