7.6: أمثلة تطبيقية
- Page ID
- 166929
لفهم المفاهيم المستفادة في هذا الفصل بشكل أفضل، قم بتطبيقها على مواقف الحياة الواقعية والمشاكل اليومية.
يظهر إجمالي مبيعات أغطية الهواتف في متجر هواتف شهير (بالآلاف) في الشكل أدناه. شهر مارس,\(2016\), يتوافق مع\(x = 0\).
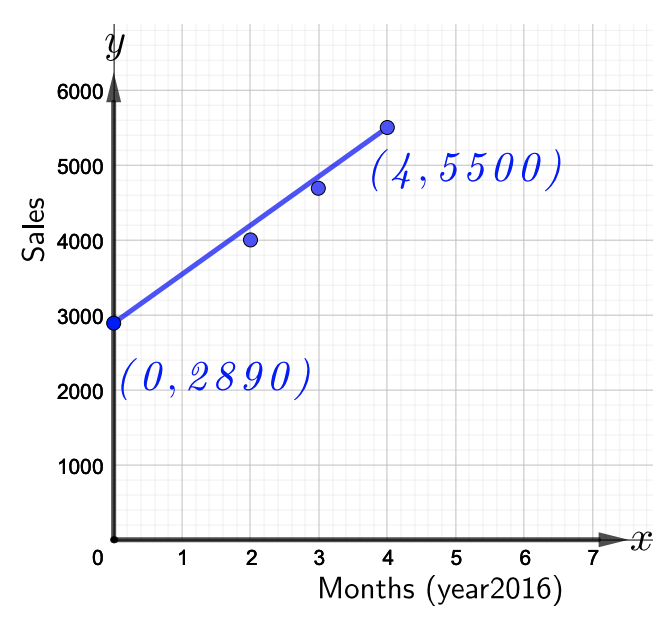
- راجع الشكل أعلاه لكتابة معادلة الخط الذي يمثل البيانات. ماذا يشير المنحدر؟
- استخدم المعادلة في الجزء أ لتقريب مبيعات أغطية الهواتف في شهر نوفمبر,\(2016\).
الحل
- بالإشارة إلى الشكل أعلاه، لاحظ أن هناك نقطتين\((0, 2890)\)\((4, 5500)\) تقعان على السطر المحدد. استخدم النقطتين لإيجاد المنحدر أولاً. وهكذا،
\(m = \dfrac{5500 − 2890}{4 − 0} = \dfrac{2610}{4} = 652.5\)
وبالتالي، فإن المنحدر هو\(652.5\). نظرًا لأن المنحدر إيجابي، فإنه يشير إلى زيادة. وبالتالي، يشير المنحدر إلى أن مبيعات أغطية الهواتف قد زادت\($652.5\) شهريًا تقريبًا من مارس\(2016\) إلى يوليو\(2016\).
استخدم المنحدر والجزء\(y\) المقطوع\((0, 2890)\) لكتابة معادلة الخط المستقيم في صورة مقطع منحدر كما يلي،
\(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &y = 652.5x + 2890 &\text{Substituting \(m = 652.5\)و\(b = 2890\)}\ end {المصفوفة}\)
- الآن، يتم إعطاء ما\(x = 0\) يتوافق مع شهر مارس وتطلب المشكلة تقريب مبيعات أغطية الهاتف في شهر نوفمبر\(2016\). وبالتالي،\(x = 8\) يتوافق مع شهر نوفمبر\(2016\). \(x = 8\)يُستعاض عن المعادلة الموجودة في الجزء أ، وهكذا،
\(\begin{array} &&y = 652.5x + 22980 &\text{Equation of the line from part a} \\ &= 652.5(8) + 2890 &\text{Substitute \(x = 8\)}\\ &= 8110 &\ text {اضرب ثم أضف لتبسيط}\\ end {المصفوفة}\)
لذلك،\(2016\) كانت مبيعات أغطية الهاتف في شهر نوفمبر تقريبًا\($8,110\).
شعرت الأم بالقلق إذا كان طفلها يستهلك كمية كافية من الكالسيوم. كان تناول الكالسيوم الرئيسي للطفل في شكل حليب. سجلت الأم البيانات لمدة تسعة أشهر لمراقبة تناول الطفل للحليب. يتم تمثيل البيانات في رسم تخطيطي مبعثر يوضح كمية الحليب التي يستهلكها الطفل كل شهر لمدة تسعة أشهر، من فبراير إلى أكتوبر كما هو موضح في الشكل أدناه.
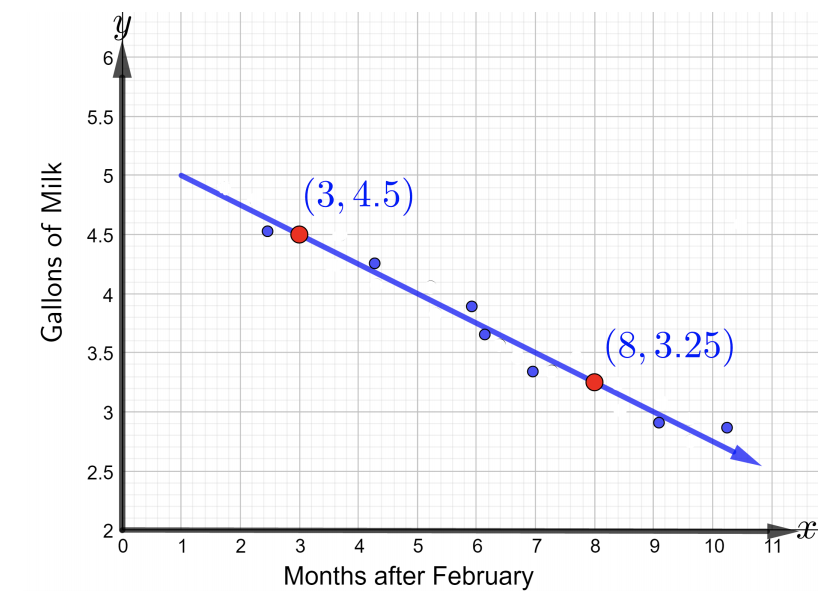
- راجع الشكل أعلاه لكتابة معادلة الخط لتمثيل البيانات المعطاة باستخدام النقطتين المسميتين. اكتب المعادلة في صورة تقاطع منحدر. ماذا يمكن أن يقال عن المنحدر؟
- استخدم معادلة الخط الموجود في الجزء أ للتنبؤ بكمية المواد الخفيفة التي سيستهلكها الطفل في ديسمبر.
الحل
- لكتابة معادلة الخط المستقيم، ابحث أولاً عن المنحدر باستخدام النقطتين المسميتين،\((3, 4.5)\) و\((8, 3.25)\). وهكذا،
\(m = \dfrac{3.25 − 4.5}{8 − 3} = −\dfrac{1.25}{5} = −0.25\)
المنحدر السلبي يعني أن استهلاك حليب الطفل يتناقص بحوالي\(0.25\) جالون من الحليب كل شهر.
نظرًا لعدم إعطاء\(y\) التقاطع، فلن يكون من الممكن استخدام نموذج اعتراض المنحدر. بدلاً من ذلك، استخدم المنحدر وأي من النقطتين المسميتين في شكل نقطة المنحدر لإيجاد معادلة الخط المستقيم. وهكذا،
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 4.5 = −0.25(x − 3) &\text{Substitute \(m = −0.25\)ونقطة\((3, 4.5)\) بـ\(x_1 = 3\) و\(y_1 = 4.5\)}\\ &y−4.5 = −0.25x+0.75 &\ text {التوزيع\(-0.25\) على كلا المصطلحين على اليمين}\\\ &y = −0.25x + 5.25 &\ text {أضف\(4.5\) إلى جانبي المساواة لحل المعادلة\(y\) والحصول عليها في نموذج التقاطع المنحدر }\ إنهاء {مصفوفة}\)
وبالتالي،\(y = −0.25x + 5.25\) هي معادلة الخط الذي يمثل البيانات الواردة في الشكل أعلاه ويكون في صورة تقاطع منحدر.
- للتنبؤ بعدد جالونات الحليب التي سيستهلكها الطفل في ديسمبر، اكتشف أولاً\(x\) أنه يتوافق مع شهر ديسمبر. يتم إعطاؤه بما\(x = 0\) يتوافق مع شهر فبراير. بدءًا من شهر مارس مع\(x = 1\)،\(x = 10\) يتوافق مع شهر ديسمبر. استبدل\(x = 10\) معادلة الخط المستقيم الموجود في الجزء أ وحلّها\(y\) كما يلي:
\(\begin{array} &&y = −0.25x + 5.25 &\text{Equation of the line found in part a} \\ &= −0.25(10) + 5.25 &\text{Substitute \(x = 10\)}\\ &= −2.5 + 5.25 &\ النص {اضرب ثم أضف لتبسيط}\\ &= 2.75\\ end {مصفوفة}\)
لذلك، سوف يستهلك الطفل حوالي\(2.75\) جالون من الحليب في ديسمبر.
تظهر المبيعات السنوية لطراز معين من الطابعات في متجر إلكترونيات شهير في الشكل أدناه، حيث\(2012\) يتوافق العام مع\(x = 0\).
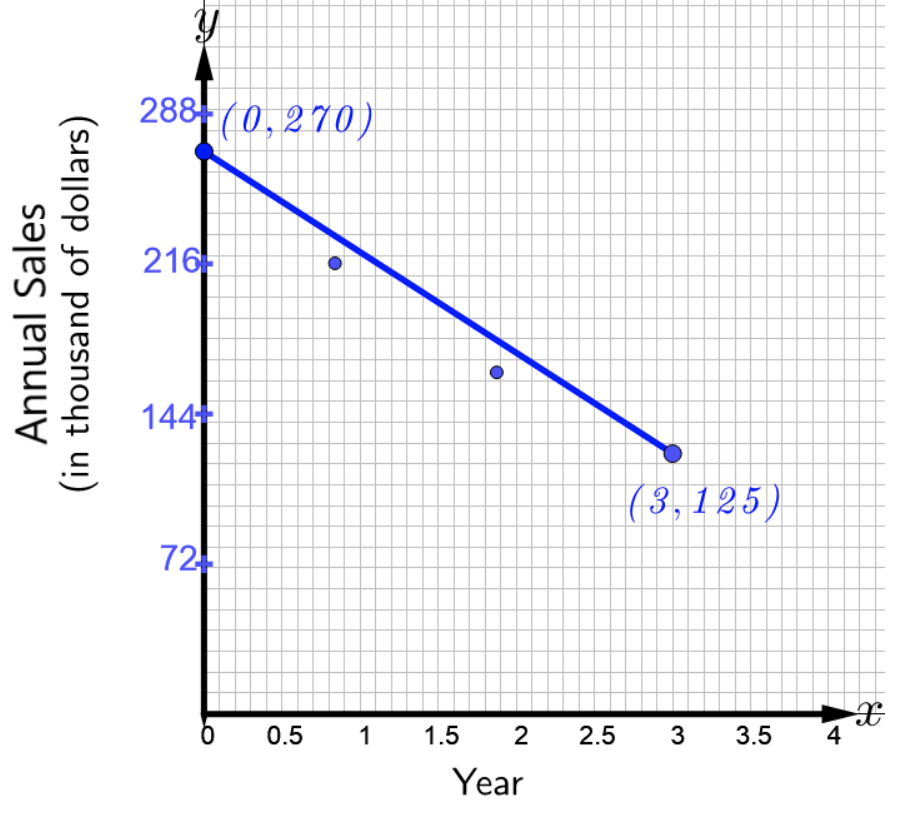
- راجع الشكل أعلاه لكتابة معادلة الخط الذي يمثل البيانات. ماذا يشير المنحدر؟
- استخدم معادلة الخط الموجود في الجزء أ لتقريب مبيعات الطابعات في السنة\(2016\).
اشترى جون مخروط آيس كريم بطول\(11.2\) سم. كان الجو حارًا حقًا، وبدأ الآيس كريم في الذوبان بمعدل\(2\) سم في الدقيقة. اهتم جون بمدى سرعة ذوبان الآيس كريم وأراد معرفة كمية الآيس كريم المتبقية بعد\(2.5\) دقائق.
- ابحث عن معادلة الخط الذي يُمثِّل البيانات في صورة التقاطع المنحدر.
- حدد كمية الآيس كريم المتبقية بعد\(2.5\) دقائق.


