Skip to main content
Global

4.12: أمثلة تطبيقية للوظائف

  1. Last updated
  2. Save as PDF
  • Page ID
    167069

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أمثلة تطبيقية للوظيفة (مشاكل الكلمات المعروفة أيضًا باسم!) يمكن أن تتخذ العديد من الأشكال.

    كن مستعدًا لاستخدام أي نوع من الوظائف التي تمت مراجعتها في هذا الفصل.

    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.12:_أمثلة_تطبيقية_للوظائف), /content/body/section[1]/header/div/h5/span/span, line 1, column 17

    تدفع الوظيفة الصيفية وقتًا ونصفًا مقابل العمل الإضافي إذا كان العامل يعمل أكثر من 40 ساعة. بعد 40 ساعة، يتقاضى العامل 1.5 ضعف سعر الساعة\($12.00\) في الساعة.

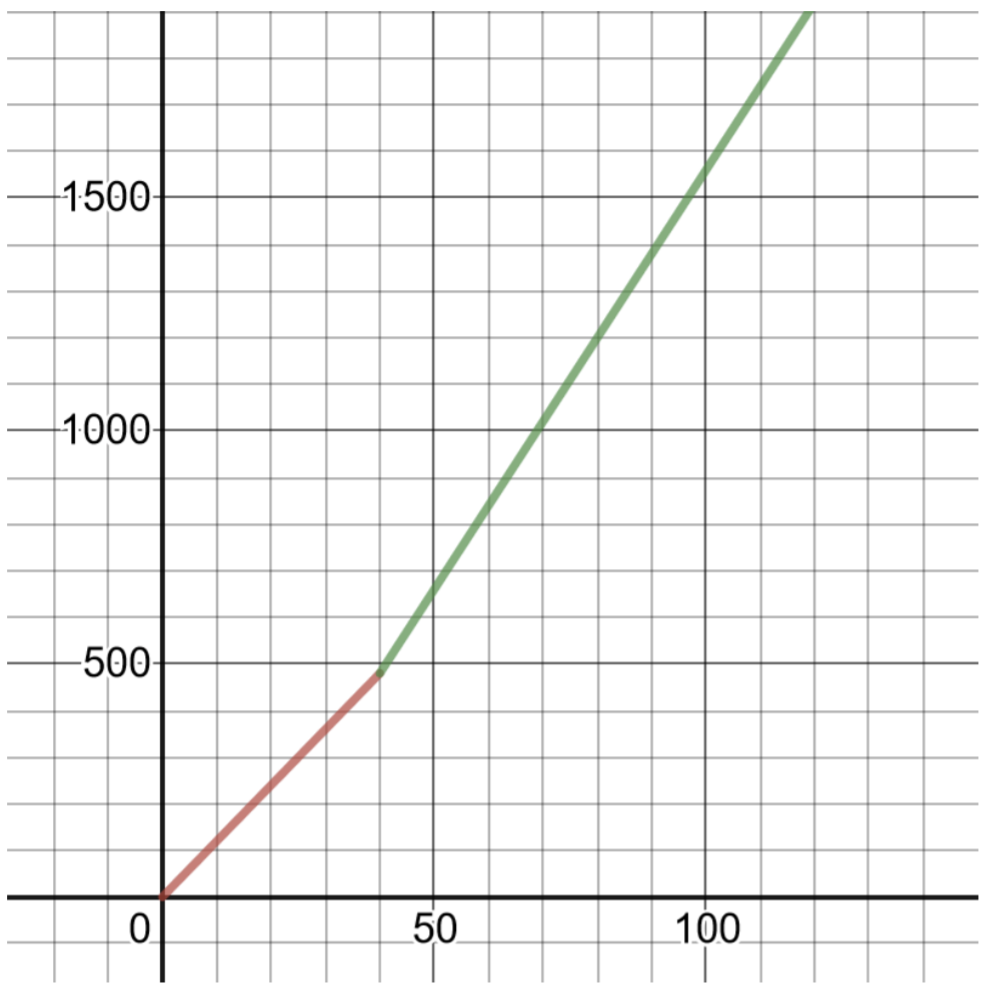
    1. اكتب ورسمًا بيانيًا دالة على شكل قطعة تعطي الأجر الأسبوعي P من حيث عدد ساعات العمل h. تلميح: قد يكون هذا صعبًا، فكر في كيفية التعبير عن عدد الساعات التي تزيد عن 40.
    2. كم سيتم كسبه من العمل لمدة 45 ساعة؟
    الحل
    1. لكتابة الدالة المكونة من قطعة:

    \(P (h) = \left\{\begin{array}{cc} 12h &0 < h \leq 40 \\ 12(40) + 1.5(12)(h − 40) &h > 40\end{array} \right.\)

    لرسم هذه الوظيفة بيانيًا، قم بعمل جدول للحلول:

    جدول الحلول لـ\(P (h) = 12h \)

    اسم النطاق\(0 < h \leq 40\)
    \(h\) \(P(h)\)
    1 \($12.00\)
    10 \($120.00\)
    40 \($480.00\)

    جدول الحلول لـ\(P (h) = 12(40) + 1.5(7)(h − 40) \)

    مبسط\(P (h) = 18h − 240 \)

    اسم النطاق\(h > 40\)
    \(h\) \(P(h)\)
    41 498
    45 570
    50 660
    60 840
    clipboard_ef0cbdf88861b06f2927739d371a66cd0.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.12:_أمثلة_تطبيقية_للوظائف), /content/body/section[1]/div/figure/figcaption/span, line 1, column 17

    1. \($570.00\)لمدة 45 ساعة من العمل (انظر جدول الحلول)
    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.12:_أمثلة_تطبيقية_للوظائف), /content/body/section[2]/header/div/h5/span/span, line 1, column 17

    ناسا تطلق صاروخًا في\(t=0\) ثوانٍ. يتم تحديد ارتفاعه، بالأمتار فوق مستوى سطح البحر، كدالة للوقت بواسطة\(h(t) = −4.9t^2 + 46t + 227\).

    1. على افتراض أن الصاروخ سينزل إلى المحيط، في أي وقت يحدث الانهيار؟
    2. ما مدى ارتفاع الصاروخ فوق مستوى سطح البحر في ذروته؟
    الحل
    1. عند بدء التشغيل\(h(t) = 0\)، قم بتعيين الدالة التي تساوي 0 والحل لـ\(t\).

    \(0 = −4.9t 2 + 46t + 227\)

    استخدم الصيغة التربيعية لحل هذه المعادلة، مع\(a = −4.9\)،\(b = 46\)،\(c = 227\)

    \(\begin{aligned} t &= \dfrac{−46 \pm \sqrt{46^2 − 4(−4.9)(227) }}{2(−4.9) } && \text{Quadratic Formula} \\ t &= \dfrac{−46 \pm \sqrt{ 2116 + 4449.2 }}{−9.8 } &&\text{Simplify the radical} \\ t &= \dfrac{46 \pm \sqrt{ 6565.2 }}{9.8 } &&\text{Further simplify the radical, divide all terms by -1 (still have } \pm\text{ )} \\t &= \dfrac{46 \pm 81.026 }{9.8 } &&\text{Square root} \\ t &= \dfrac{46 + 81.026 }{9.8 } &&\text{Addition} \\ t &= \dfrac{46 − 81.026 }{9.8} && \text{Subtraction} \\ t& = 12.96 \text{ and } t = −3.57&& \text{Two solutions, reject negative solution because time cannot be negative} \\ t &= 12.96 \text{ seconds }&&\text{Final Answer} \end{aligned}\)

    1. ما مدى ارتفاع الصاروخ فوق مستوى سطح البحر في ذروته؟

    \(h(t) = −4.9t^2 + 46t + 227\)تُظهر علامة معامل الحد الرئيسي للدالة التربيعية الطريقة التي يفتح بها المكافئ. المعامل هو\(−4.9\)، وبما أنه سلبي، فإن الدالة التربيعية تنفتح لأسفل.

    الآن نحن بحاجة إلى العثور على قمة الرأس. ستظهر القيمة y للزوج الذي تم ترتيبه في قمة الرأس من أين يبدأ النطاق.

    قمة الرأس هي\(\left(− \dfrac{b }{2a} , f\left( −\dfrac{ b }{2a}\right) \right)\)، مع\(a = −4.9\) و\(b = 46\)

    قمة الرأس هي\(\left(−\dfrac{ 46 }{2(−4.9) }, f\left( − \dfrac{46 }{2(−4.9)}\right)\right)\)

    قمة الرأس\((4.694, f (4.694))\) هي\((4.694, (−4.9)(4.694)^2 + (46)(4.694) + 227 ))\) أو\((4.694, 334.959)\)

    يبلغ ارتفاع الصاروخ في ذروته\(334.959\) أمتار فوق مستوى سطح البحر.

    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.12:_أمثلة_تطبيقية_للوظائف), /content/body/section[3]/header/div/h5/span/span, line 1, column 17

    للترويج للمبيعات الجماعية لرحلة بحرية في ألاسكا، تقوم وكالة سفر بتخفيض سعر التذكرة العادي\($5\) لكل شخص في المجموعة.\($4500\)

    1. اكتب معادلة خطية توضح التكلفة لكل شخص\(f(p)\)، إذا كان\(p\) الأشخاص يسافرون في المجموعة.
    2. استخدم المعادلة لتحديد التكلفة لـ 50 شخصًا.
    الحل
    1. نظرًا لأن تكلفة الفرد تنخفض بنفس المبلغ لكل شخص، فهذه معادلة خطية.

    استخدمها\(f(x) = mx + b\)، أو دعنا نكتبها بالطريقة نفسها\(f(p) = mp + b\)، مع\(f(p)\) التكلفة لكل شخص.

    \(f(p) = mp + b\)

    نظرًا لانخفاض تكلفة الفرد بمقدار 5 دولارات لكل شخص في المجموعة، فهذا هو منحدر الخط.

    \(\begin{aligned} f(p)&= −5p + b && \text{Slope-intercept form of the equation of a line} \\ f(p) &= −5p + 4500 &&\text{The y-intercept is the starting point, so the regular ticket price of }$4500 {is the y-intercept} \\ f(p)& = −5p + 4500 && \text{Linear Equation} \end{aligned}\)

    1. استخدم المعادلة لتحديد التكلفة لـ 50 شخصًا.

    \(\begin{aligned} f(50) &= −5(50) + 4500 && \text{Replace p with 50 people in the Linear Equation} \\ f(50) &= −250 + 4500 &&\text{Simplify} \\ f(50) &= 4250 &&\text{Simplify} \\ \text{If }50 &\text{ people take the cruise, the cost per-person for the cruise is } $4250&&\text{Final Answer }\end{aligned}\)

    التمرين
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.12:_أمثلة_تطبيقية_للوظائف), /content/body/section[4]/header/div/h5/span/span, line 1, column 17

    أكمل مشكلات الوظيفة المطبقة التالية:

    1. يتقاضى الخياط رسومًا أساسية\($20\) إضافية\($5\) لكل حرف لخياطة اسم رياضي على ظهر السترة.
      1. اكتب معادلة خطية تجد تكلفة وجود اسم يحتوي على حرف x مخيط على ظهر السترة.
      2. ما هي تكلفة الاسم الذي يتكون من 11 حرفًا؟
    2. في أكابولكو بالمكسيك، من المعالم السياحية الشهيرة مشاهدة الرجال وهم يغوصون من منحدر إلى الماء على ارتفاع 75 قدمًا. يتم تحديد ارتفاع الغواص\(f(t)\) فوق الماء (بالأقدام) بعد\(t\) ثوانٍ من الغوص\(f(t) = −16t^2+75\).
      • إلى متى يستمر الغوص؟
    3. في بلد معين، يتم تقييم ضريبة الدخل على النحو التالي: لا توجد ضريبة على الدخل حتى\($15000\). \($30000\)يتم فرض ضريبة على الدخل الزائد\($15000\) وما يصل إلى\(12%\). \($30000\)يتم فرض ضريبة على الدخل الزائد في\(18%\).
      1. اكتب الدالة النقطية للمعلومات الواردة أعلاه وارسم الرسم البياني الخاص بها.
      2. حدد مبلغ الضريبة الواجب دفعها على دخل قدره\($18000\).