Skip to main content
Global

4.11: وظائف متعددة التعريف

  1. Last updated
  2. Save as PDF
  • Page ID
    166983

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    تعريف: وظائف محددة بعدة طرق

    الوظائف المحددة بدقة متعددة هي وظائف يتم تحديدها باستخدام معادلات مختلفة لأجزاء مختلفة من المجال.

    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.11:_وظائف_متعددة_التعريف), /content/body/section[2]/header/div/h5/span/span, line 1, column 17

    أوجد الدالة التالية المُعرَّفة بدقة متعددة للقيم المُعطاة للدالة\(x\)، وارسم رسماً بيانيًا لها:

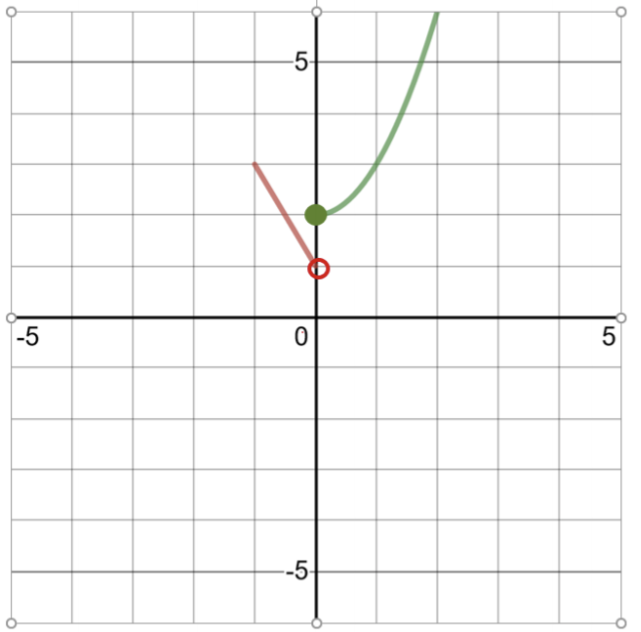
    \(f(x) = \left\{\begin{array}{cc}−2x + 1 & −1 \leq x < 0 \\ x^2 + 2 &0 \leq x \leq 2\end{array} \right.\)

    الحل

    لرسم هذه الوظيفة بيانيًا، قم بعمل جدول للحلول:

    جدول الحلول لـ\(f(x) = −2x + 1 \)

    اسم النطاق\(−1 \leq x < 0\)
    \(x\) \(f(x)\)
    -1 3
    0 1 (افتح الدائرة هنا، 0 ليس في المجال)

    جدول الحلول لـ\(f(x) = x^2 + 2\)

    اسم النطاق\(0 \leq x \leq 2\)
    \(x\) \(f(x)\)
    0 2
    1 3
    2 6
    clipboard_e94fd5197718a7373772af1280306cf06.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.11:_وظائف_متعددة_التعريف), /content/body/section[2]/div/figure/figcaption/span, line 1, column 17
    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.11:_وظائف_متعددة_التعريف), /content/body/section[3]/header/div/h5/span/span, line 1, column 17

    أوجد الدالة التالية المُعرَّفة بدقة متعددة للقيم المُعطاة للدالة\(x\)، وارسم رسماً بيانيًا لها:

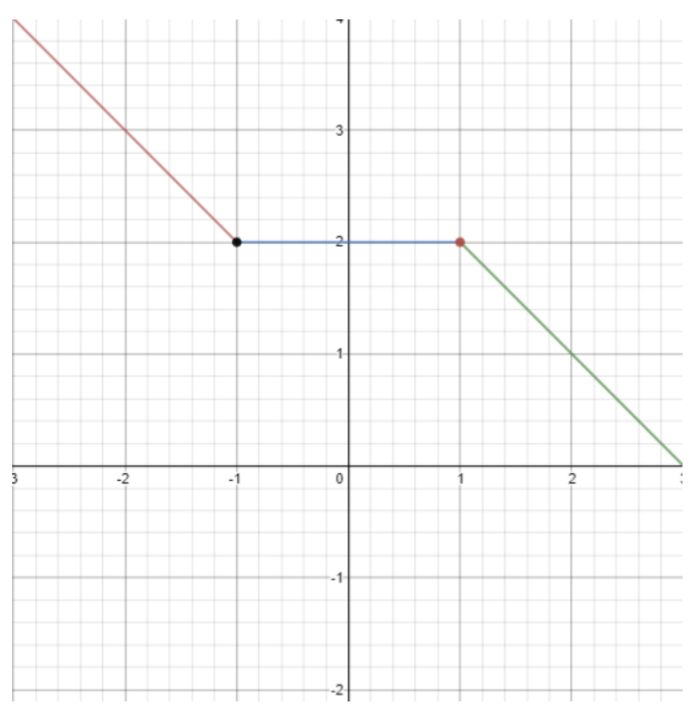
    \(f(x) = \left\{\begin{array}{cc} −x + 1 &x \leq −1 \\ 2 & −1 < x \leq 1 \\ −x + 3 &x > 1 \end{array}\right.\)

    الحل

    لرسم هذه الوظيفة، قم مرة أخرى بعمل جدول للحلول:

    جدول الحلول لـ\(f(x) = −x + 1\)

    اسم النطاق\(x \leq −1\)
    \(x\) \(f(x)\)
    -3 4
    -2 3
    -1 2 (دائرة مغلقة هنا، -1 في المجال)

    جدول الحلول لـ\(f(x) = 2\)

    اسم النطاق\(−1 < x \leq 1\)
    \(x\) \(f(x)\)
    -1 2 (دائرة مفتوحة مملوءة بالوظيفة السابقة، -1 ليست في المجال)
    0 2
    1 2 (دائرة مغلقة هنا، 1 في المجال)

    جدول الحلول لـ\(f(x) = −x + 3\)

    اسم النطاق\(x > 1\)
    \(x\) \(f(x)\)
    1 2 (دائرة مفتوحة مملوءة بالوظيفة السابقة، 1 ليست في المجال)
    2 1
    3 0
    clipboard_e795cd2fce50083772c8741bdcad72855.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.11:_وظائف_متعددة_التعريف), /content/body/section[3]/div/figure/figcaption/span, line 1, column 17
    التمرين
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.11:_وظائف_متعددة_التعريف), /content/body/section[4]/header/div/h5/span/span, line 1, column 17

    قم بتقييم الدوال التالية المحددة بدقة لقيم x المعطاة، ورسم الدوال بيانيًا:.

    1. \ (f (x) =\ يسار\ {\ ابدأ {\ مصفوفة} {cc}
      x وx<0\\
      2 x+1 &x\ geq 0
      \ end {المصفوفة}\ اليمين.\)
    2. \(g(x) = \left\{\begin{array}{cc} 4 − x& x < 2\\ 2x − 2 &x \geq 2 \end{array} \right.\)
    3. \(h(x) = \left\{\begin{array}{cc} −x − 1 & x < −1 \\ 0& −1 \leq x \leq 1 \\ x + 1 & x > 1 \end{array} \right.\)
    4. \(g(x) = \left\{\begin{array}{cc} 6 & −8 \leq x < −4 \\ 3 &−4 \leq x \leq 5 \end{array}\right.\)
    5. \(f(x) = \left\{\begin{array}{cc} −x + 1 & −1 \leq x < 1 \\ \sqrt{x − 1 } &1 \leq x \leq 5\end{array}\right.\)