4.8: تمثيل الدوال البيانية (بدون استخدام حساب التفاضل والتكامل)

Last updated
Save as PDF

Page ID: 167015

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

هناك بعض الوظائف الأساسية، التي تسمى وظائف مجموعة الأدوات، والتي يجب على الطلاب التعرف عليها من خلال تعريف الوظيفة والرسم البياني الخاص بهم. لكل وظيفة من هذه الوظائف،\(x\) هو متغير الإدخال،\(f(x)\) وهو متغير الإخراج. الرسومات التالية مأخوذة من كتاب OER Business Calculus من تأليف Calaway و Hoffman و Lippman، 2013 ويتم استخدامها بإذن (رخصة Creative Commons Attribution 3.0 بالولايات المتحدة).

الشكل
ParseError: invalid ArgList (click for details)
Callstack: at (اللغة_العربية/(__)/04:_الوظائف/4.08:_تمثيل_الدوال_البيانية_(بدون_استخدام_حساب_التفاضل_والتكامل)), /content/body/figure[1]/figcaption/span, line 1, column 17

على عكس مساق STEM Calculus I التقليدي، لا تقوم دورة حساب التفاضل والتكامل للأعمال والعلوم الاجتماعية هذه بتدريس وظائف الرسوم البيانية باستخدام تحويلات الدوال.

يُتوقع من الطلاب في هذا الفصل إعداد جدول الحلول ورسم الدالة بيانيًا. سيتعلم الطلاب أيضًا كيفية رسم الوظائف باستخدام حساب التفاضل والتكامل!

مثال

ParseError: invalid ArgList (click for details)

Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.08:_تمثيل_الدوال_البيانية_(بدون_استخدام_حساب_التفاضل_والتكامل)), /content/body/section/header/div/h5/span/span, line 1, column 17

رسم بياني للوظائف التالية:

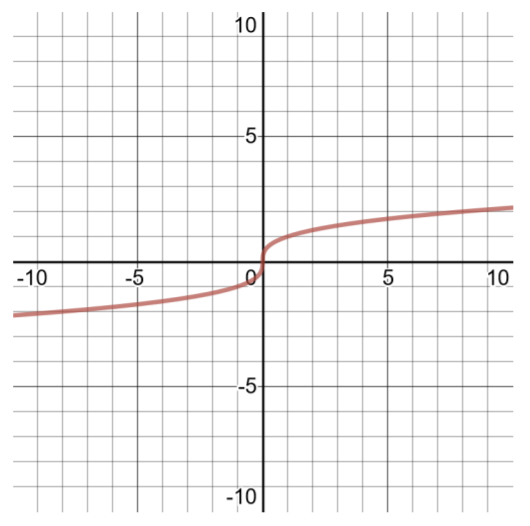
\(f(x) = \sqrt[3]{x}\)
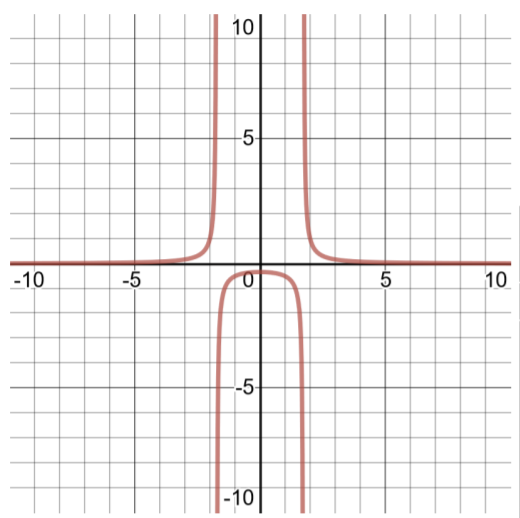
\(f(x) = \dfrac{1 }{x^2 − 3}\)

الحل

قم بعمل جدول للحلول وحدد مجال الوظيفة.

جدول الحلول\(f(x) =\sqrt[3]{x}\) للنطاق\((−\infty , \infty )\)
\(x\)	\(f(x)\)
-8	-2
-1	-1
0	0
1	1
8	2

قم بعمل جدول للحلول وحدد مجال الوظيفة. لتحديد مجال هذه الدالة الكسرية، انتبه إلى المقام. لا يمكن أن يساوي المقام 0. قم بتعيين المقام = 0 لحل x والعثور على القيم التي لن يُسمح بها لـ x.

\(\begin{aligned} f(x) &= \dfrac{1 }{x^2 − 3}\\ 0 &= x^2 − 3 \\3 &= x^2 \\ \pm \sqrt{3} &=\sqrt{x^2} \\ \pm \sqrt{3}& = x \end{aligned}\)

يجب استبعاد هذه الأرقام من مجال هذه الدالة\(−\sqrt{3}\) (حوالي −1.732)) و\(\sqrt{3}\) (حوالي 1.732)).

لرسم هذه الدالة بيانيًا بشكل صحيح، من المهم فحص السلوك حول هذه الأرقام المستبعدة من المجال. وبالتالي، فإن سبب وجود العديد من الأزواج المرتبة في جدول الحلول. فكر في الأمر على النحو التالي: ابدأ بنطاق\((−\infty , \infty )\)، ولكن يجب إزالة أي أرقام من شأنها أن تسبب مشاكل (كما هو الحال في هذه الحالة، الأرقام التي ستجعل مقام الدالة 0، لأن القسمة على 0 غير محددة). يعد رسم مثل هذه الوظائف يدويًا أمرًا شاقًا للغاية، ولكنه مهارة مهمة للطالب حتى ينجح في حساب التفاضل والتكامل للأعمال والعلوم الاجتماعية.

جدول الحلول\(f(x) = \sqrt[3]{ x}\) للنطاق\((−\infty , \infty )\)
\(x\)	\(f(x)\)
-4	0.077
-3	0.167
-2	1
-1.5	-1.333
-1	-0.5
-0.5	-0.364
0	0
0.5	-0.364
1	-0.5
1.5	-1.333
2	1
3	0.167
4	0.077

مشكلات الممارسة: ارسم الوظائف التالية بيانيًا، مع الانتباه إلى مجال الدالة.

\(f(x) = 2x^3\)
\(f(x) = \dfrac{1 }{2x^2}\)
\(f(x) = 4 \vert x − 2 \vert\)
\(f(x) = \dfrac{1 }{3} x − 12 \)
\(f(x) = \dfrac{1 }{x − 7}\)
\(f(x) = 3\sqrt{2x^3 + 1}\)