4.6: دوال كثيرة الحدود
- Page ID
- 167029
الدالة متعددة الحدود هي دالة يمكن كتابتها بالشكل العام:
\(f(x) = a_n x^n + a_{n−1} x^{n−1 }+ ... + a_1x + a_0\)
لعدد صحيح غير سالب، يسمى درجة متعدد الحدود.\(n\) المعاملات\(a_0\)،،\(a_1\)\(\ldots\)، و هي أرقام حقيقية بالمعامل الرائد an\(a_n \neq 0\). مجال دالة كثيرة الحدود هو\((−\infty , \infty )\). \(n\)يمكن أن يتقاطع الرسم البياني لدالة متعددة الحدود للدرجة مع المحور السيني في معظم\(n\) الأوقات. هذه هي جذور الدالة متعددة الحدود.
لا توجد أمثلة أو واجبات منزلية في هذا القسم.
الدوال التربيعية
\(f(x) = ax^2 + bx + c\)أين\(a\neq 0\)
هي دالة تربيعية في الصورة القياسية، ورسمها البياني عبارة عن مكافئ. عندما يكون المعامل الرئيسي\(a\) موجبًا، ينفتح الرسم البياني للدالة التربيعية لأعلى. عندما يكون المعامل الرئيسي\(a\) سالبًا، يُفتح الرسم البياني للدالة التربيعية نحو الأسفل.
ارسم رسمًا بيانيًا\(f(x) = −x^2 + 5x + 3\) في نظام إحداثيات مستطيل. أوجد رأس المنحنى، والجزء المقطوع من السينات، والجزء المقطوع من محور الصادات جبريًّا.
الحل
ابحث عن قمة الرأس بالحساب\(\left(\dfrac{-b}{2 a}, f\left(\dfrac{-b}{2 a}\right)\right)\) باستخدام\(a = −1\)\(b = 5\) و\(c = 3\).
\ (\ ابدأ {محاذاة}
\ يسار (\ dfrac {-b} {2 أ}، f\ يسار (\ dfrac {-b} {2 أ}\\ يمين)\ ==&&\ نص {ابحث عن رأس البارابولا}\\
\ dfrac {-5} {2 (-1)} &=\\
\ dfrac {5} {5} {2} &=2.5\\ text {تبسيط}\\
\ dfrac {-5} {2 (-1)} &=2.5\\\
f (2.5) &=- (2.5) ^ {2} +5 (2.5) +3=9.25=&F\ يسار (\ dfrac {-b} {2 أ}\\ يمين) =9.25\\\ يسار (\ dfrac {-b} {2 أ}، f\ يسار (\ dfrac {-b} {2 أ}\ يمين)\ = (2.5، 9.25) &\ text {قمة البارابولا}
\ النهاية {aligned}\)
للعثور على عمليات الاعتراض:
\ (\ ابدأ {aligned} 0&=-x^ {2} +5 x+3 &\ text {x-Intercept، set} f (x) =0\\ 0&=-x^ {2} +5 x+3\\ text {استخدم الصيغة التربيعية لحل هذه المعادلة (لا يمكن أخذها في الاعتبار). دع} a=-1، b=5، c=3\\ x&=\ dfrac {-5\ pm\ sqrt {(5) ^ {2} -4 (-1) (3)}}}} {2 (-1)} و\ النص {الصيغة التربيعية
}\\\ x&=\ dfrac {-5\ pm\ sqrt {37}} {-2} و\ {تبسيط النص}\
x&=-0.54\ text {أو} x=5.54 &\ text {تحتوي هذه الوظيفة التربيعية على جذرين (x-intercepts). }\\ f (0) &=-0^ {2} +5 (0) +3 &\ text {y-Intercept، set} x=0\\ f (0) &=3\\ text {y-Intercept}\ النهاية {محاذاة}\)
قم برسم بياني للأزواج الأربعة المرتبة، واحسب الأزواج الأكثر ترتيبًا إذا لزم الأمر:\((2.5, 9.25)\)،\((−.54, 0)\)،\((5.54, 0)\)،\((0, 3)\).

Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.06:_دوال_كثيرة_الحدود), /content/body/div[1]/section[2]/div/figure/figcaption/span, line 1, column 17
- \(f(x) = 2x ^2 − 5x − 5\)
- \(f(x) = 0.5x ^2 − 6x + 21\)
- \(f(x) = −4x ^2 − 8x − 3\)
- \(f(x) = −4x^ 2 + 16x − 15\)
- \(f(x) = x^ 2 − 8x + 12\)
- \(f(x) = −7x^ 2 + 100x − 10\)
الدوال التكعيبية والدوال العليا
الدالة التكعيبية هي دالة كثيرة الحدود من الدرجة الثالثة يمكن كتابتها بالشكل العام:
\(f(x) = a_3x^ 3 + a_2x^2 + a_1x + a_0\)
مع 3 كدرجة الدالة التكعيبية. المعاملات\(a_0\)،،\(a_1\)\(a_2\)،\(a_3\) هي أرقام حقيقية ذات معامل رائد\(a_3 \neq 0\). مجال الدالة التكعيبية هو\((−\infty , \infty )\).
ضع في اعتبارك إن أمكن وقم برسم الدالة عن طريق إنشاء جدول الحلول:
\(f(x) = x^3 − 4x^2 + 6x − 1\)
الحل
هذا الرقم متعدد الحدود من الدرجة 3، ويصعب حسابه. قم بإنشاء جدول حلول للرسم البياني.

Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.06:_دوال_كثيرة_الحدود), /content/body/div[2]/section[2]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(f(x) = x^3 − 4x^2 + 6x − 1\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^3 − 4(−2)^2 + 6(−2) − 1 = −37\) |
| -1 | \(f(−1) = (−1)^3 − 4(−1)^2 + 6(−1) − 1 = −12\) |
| 0 | \(f(0) = (0)^3 − 4(0)^2 + 6(0) − 1 = −1\) |
| 1 | \(f(1) = (1)^3 − 4(1)^2 + 6(1) − 1 = 2\) |
| 2 | \(f(2) = (2)^3 − 4(2)^2 + 6(2) − 1 = 3\) |
ضع في اعتبارك إن أمكن وقم برسم الدالة عن طريق إنشاء جدول الحلول:
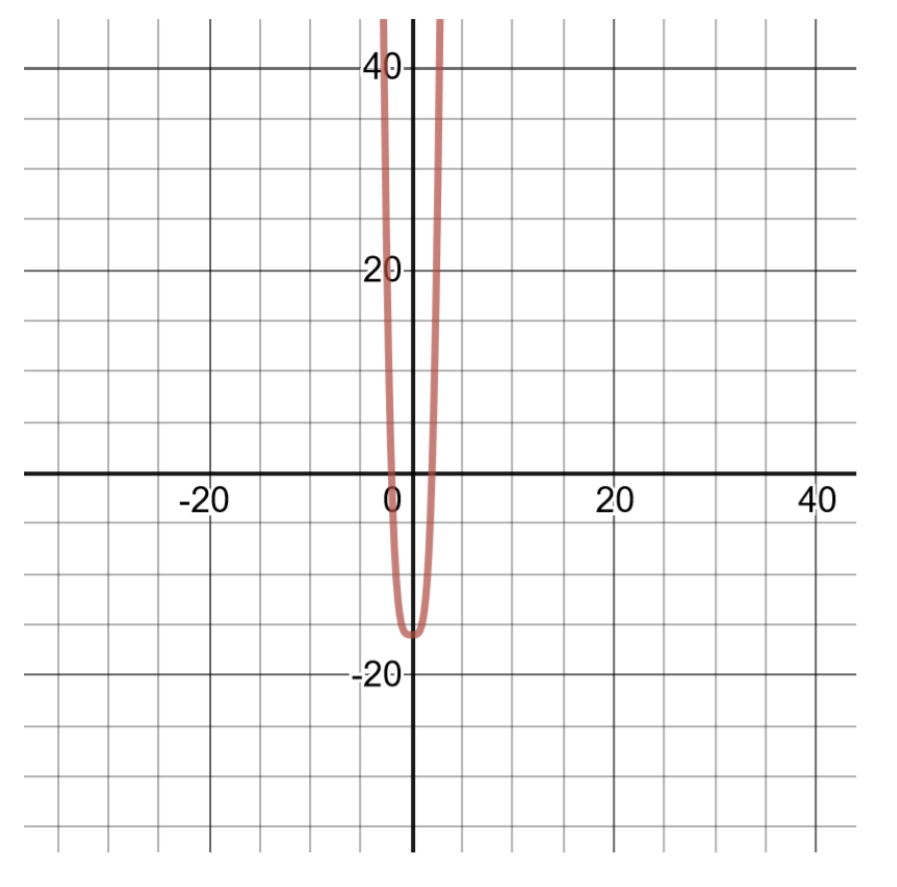
\(g(x)=x^4-16\)
الحل
هذا العدد الكبير من الحدود هو من الدرجة 4، ولأنه فرق بين المربعات، يمكن أخذه في الاعتبار في حاصل ضرب المقادير ذات الحدين لإيجاد أصفار كثيرة الحدود. قم بإنشاء جدول حلول للرسم البياني.
\(\begin{aligned} g(x)&=\left(x^{2}-4\right)\left(x^{2}+4\right) && \text{Factoring into the sum and difference of binomials.} \\ g(x)&=(x-2)(x+2)\left(x^{2}+4\right) && \text{Further factoring. Set each binomial equal to zero to find the real number zeroes of the polynomial.} \\ x-2&=0, x=2 && \text{The first real number zero of the polynomial, }(2,0) \\ x+2&=0, x=-2 &&\text{The second real number zero of the polynomial, } (2,0) \\ x^{2}+4&=0, x^{2}=-4 && \text{The third binomial factor does not produce real number zeroes, } \\ & &&\text{because no number squared can result in a negative value.} \end{aligned}\)
Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.06:_دوال_كثيرة_الحدود), /content/body/div[2]/section[3]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(g(x)=x^4-16\) | |
| \(x\) | \(g(x)\) |
| -2 | \(g(−2) = (−2)^4 − 16 = 16 − 16 = 0\) |
| -1 | \(g(−1) = (−1)^4 − 16 = 1 − 16 = −15\) |
| 0 | \(g(0) = (0)^4 − 16 = 0 − 16 = −16\) |
| 1 | \(g(1) = g(1) = (1)^4 − 16 = 1 − 16 = −15\) |
| 2 | \(g(2) = g(2) = (2)^4 − 16 = 16 − 16 = 0\) |
ضع في اعتبارك إن أمكن وقم برسم الدالة عن طريق إنشاء جدول الحلول:
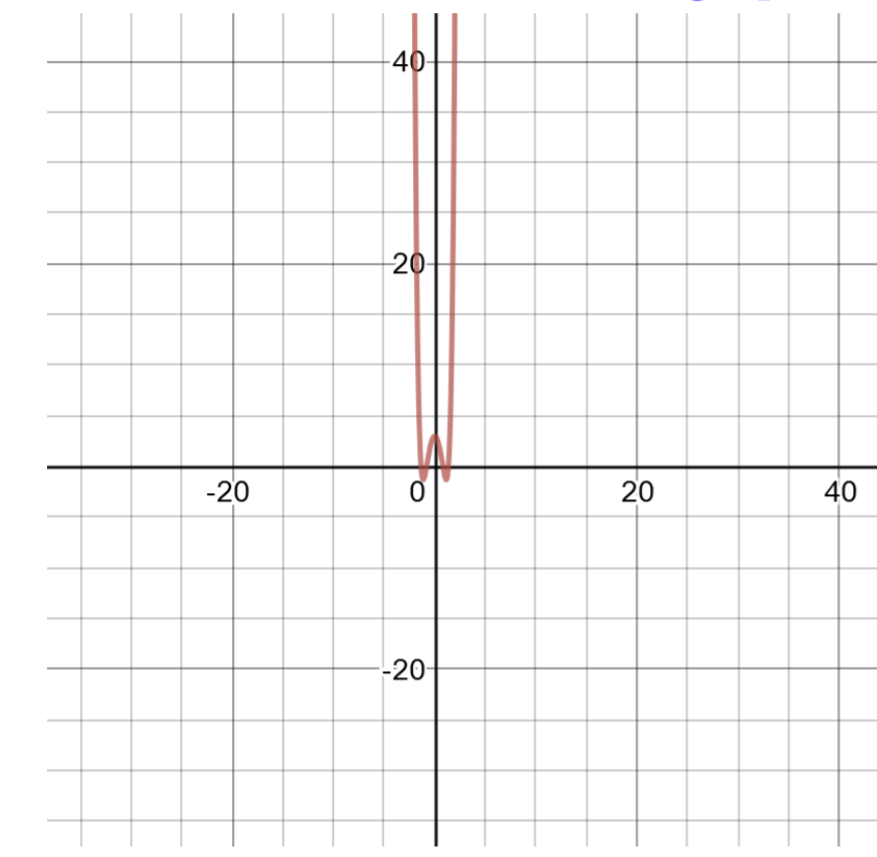
\(f(x) = x ^6 − 5x ^2 + 3\)
الحل
هذا الرقم متعدد الحدود من الدرجة 6، ويصعب حسابه. قم بإنشاء جدول حلول للرسم البياني.
Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.06:_دوال_كثيرة_الحدود), /content/body/div[2]/section[4]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(f(x) = x ^6 − 5x ^2 + 3\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^6 − 5(−2)^2 + 3 = 47\) |
| -1 | \(f(−1) = (−1)^6 − 5(−1)^2 + 3 = −1\) |
| 0 | \(f(0) = (0)^6 − 5(0)^2 + 3 = 3\) |
| 1 | \(f(1) = (1)^6 − 5(1)^2 + 3 = −1\) |
| 2 | \(f(2) = (2)^6 − 5(2)^2 + 3 = 47\) |
- \(f(x) = x^3 − 27\)
- \(g(x) = 81x ^4 − 16\)
- \(h(x) = 2x ^5 − 4x ^2 − 6x + 3\)
- \(f(x) = 5x ^6 − 6x ^4 + 5\)
الدوال العقلانية
الدالة الكسرية هي دالة يمكن كتابتها في صورة حاصل قسمة لكثيرات الحدود.
\(f(x) = \dfrac{P (x) }{Q(x) }\)،\(Q(x) \neq 0\)
حيث\(Q(x)\) توجد\(P(x)\) وكثيرات الحدود في متغير واحد\(x\). المجال هو مجموعة جميع الأرقام الحقيقية من هذا القبيل\(Q(x) \neq 0\).
بالنسبة للوظيفة،\(f(x) = \dfrac{9 }{x − 3}\):
- رسم بياني للدالة
- قم بتقييم الدالة لـ\(x = 0\) و\(x = 2\)
الحل
انتبه إلى مجال هذه الوظيفة. القسمة على الصفر غير محددة، لذلك يجب استبعاد الرقم (الأرقام) الذي سيجعل المقام 0 من المجال.
في هذه المشكلة،\(x − 3\) يقع في مقام الدالة. \(x − 3 = 0\)ضعيها وحلّها\(x\). إذا كانت\(x = 3\) القسمة غير محددة، فاستبعد الرقم 3 من مجال الدالة. فكر في الأمر على أنه يبدأ دائمًا بجميع الأرقام الحقيقية\((−\infty , \infty )\) ثم أزل القيم التي ستؤدي إلى تقسيم غير محدد.
مجال هذه الوظيفة هو\((−\infty , 3) \cup (3, \infty )\).
غالبًا ما تحتوي الدوال الكسرية على خطوط تقارب، وهو خط يقترب باستمرار من منحنى معين ولكنه لا يلتقي به عند أي مسافة محدودة. سوف تتعلم عن خطوط التقارب في قسم رسم المنحنيات في Math 162.
يمكن العثور على الرسم البياني لهذه الوظيفة من خلال إنشاء جدول الحلول:

Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.06:_دوال_كثيرة_الحدود), /content/body/div[3]/section[2]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(f(x) = \dfrac{9 }{x − 3}\) | اسم النطاق:\((−\infty , 3) \cup (3, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | \(-\dfrac{9}{7}\) |
| -3 | \(-\dfrac{3}{2}\) |
| -2 | \(-\dfrac{9}{5}\) |
| -1 | \(-\dfrac{9}{4}\) |
| 0 | \(-3\) |
| 1 | \(-\dfrac{9}{2}\) |
| 2 | \(-9\) |
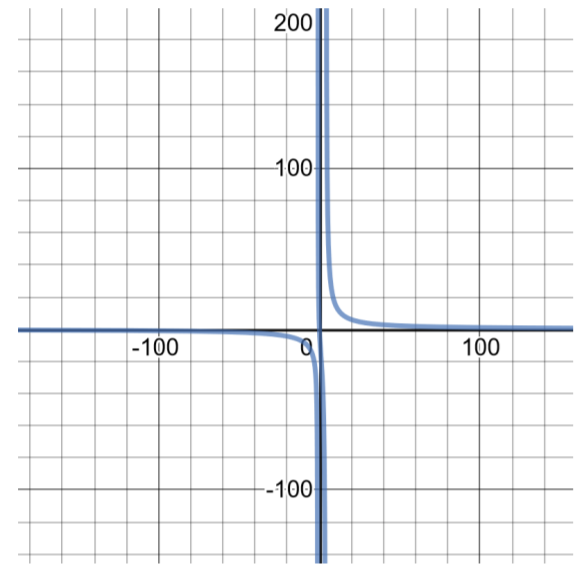
بالنسبة للوظيفة،\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\)
- رسم بياني للدالة
- قم بتقييم الدالة لـ\(x = −1\) و\(x = 3\)
الحل
انتبه إلى مجال هذه الوظيفة. القسمة على الصفر غير محددة، لذلك يجب استبعاد الرقم (الأرقام) الذي سيجعل المقام 0 من المجال.
في هذه المشكلة،\(x^2 − 3x − 4\) يقع في مقام الدالة. قم بحساب المقدار التربيعي للحصول على\((x − 4)(x + 1)\) كل عامل يساوي صفرًا وتعيينه وحل لـ\(x\):\(x − 4 = 0\)، إذن\(x = 4\)؛\(x + 1 = 0\)، إذن\(x = −1\). إذا كانت القسمة\(x = 4\) أو\(x = −1\)، غير محددة، فاستبعد الرقمين 4 و−1 من مجال الدالة. فكر في الأمر على أنه يبدأ دائمًا بجميع الأرقام الحقيقية\((−\infty , \infty )\) ثم أزل القيم التي ستؤدي إلى تقسيم غير محدد.
مجال هذه الوظيفة هو\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\). يمكن العثور على الرسم البياني لهذه الوظيفة من خلال إنشاء جدول الحلول:
Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.06:_دوال_كثيرة_الحدود), /content/body/div[3]/section[3]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\) | اسم النطاق:\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | −16.667 |
| -3 | −21.429 |
| -2 | −33.333 |
| -1 | غير محدد |
| 0 | 0 |
| 1 | −16.667 |
| 2 | −33.333 |
| 3 | -75 |
| 4 | غير محدد |
- \(f(x) = \dfrac{3x + 6 }{x − 1}\)
- \(f(x) = \dfrac{9 }{x^2 − 9}\)
- \(f(x) = \dfrac{x^ 2 − 4 }{x^2 − 4x}\)


