4.5: وظائف القيمة المطلقة
- Page ID
- 167012
لرسم دوال القيمة المطلقة بيانيًا، اختر قيمًا صغيرة للدالة المعطاة واحسب قيمتها لإنشاء أزواج مرتبة.\(x\)\(f(x)\) ثلاثة أزواج مرتبة هي الحد الأدنى للمبلغ المطلوب لرسم دالة القيمة المطلقة. كن حذرًا، لأن زوجًا واحدًا مرتبًا يجب أن يمثل قمة الرأس، وهي النقطة التي يلتقي فيها الجانبان الأيسر والأيمن للدالة. لرسم شكل دالة القيمة المطلقة بشكل صحيح، يجب العثور على قمة الرأس.
\(f(x) = a\vert x − h\vert+ k\)الشكل العام لدالة القيمة المطلقة، باستخدام الرأس\((h,k)\)
- \(a\)يحدد كلاً من العرض والاتجاه (المواجه لأعلى أو لأسفل) للوظيفة.
- \(h\)هو التحول الأفقي من الأصل.
- \(k\)هو التحول الرأسي من الأصل.
ابدأ بتحديد الزوج المُرتب من قمة الرأس، ثم ابحث عن زوج واحد مرتب على يسار الأصل، وعلى يمين الأصل. اختر قيمة x بوحدة واحدة على يسار قيمة x الخاصة بالأصل،\(f(x)\) واحسب ثم اختر وحدة قيمة x واحدة على يمين قيمة x الخاصة بالأصل وقم بالحساب\(f(x)\). سيشبه الرسم البياني أ\(V\)، إما متجهًا لأعلى أو لأسفل، اعتمادًا على علامة\(a\).
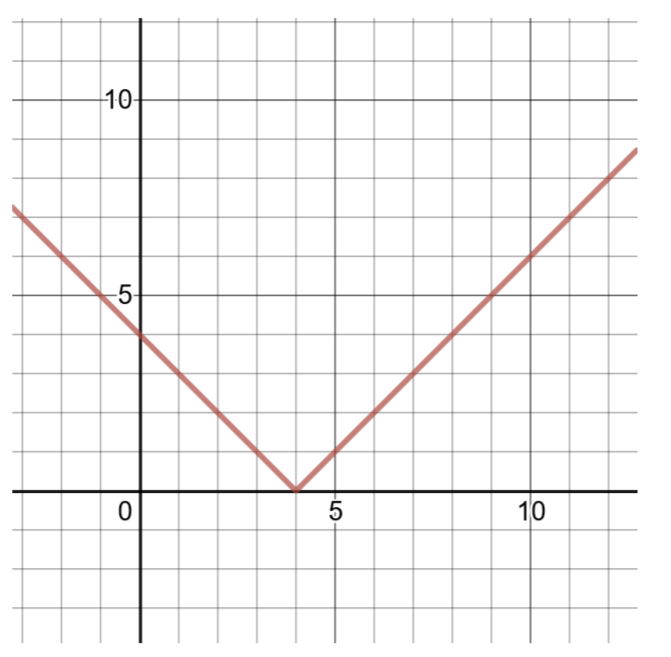
قم بإنشاء جدول للحلول ورسم دالة القيمة المطلقة التالية:
\(f(x) = \vert x − 4\vert\)
الحل
مقارنة هذه الدالة بالشكل العام لوظائف القيمة المطلقة (كما هو موضح أعلاه)،\(a = 1\)،\(h = 4\)،\(k = 0\). قمة الرأس هي\((h, k)\) أو\((4, 0)\).
للعثور على زوجين آخرين مُرتَّبين، اختر\(x = 3\) قيم ثم قم بحسابها\(f(x)\).\(x = 5\)
Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.05:_وظائف_القيمة_المطلقة), /content/body/section[1]/div/figure/figcaption/span, line 1, column 17
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">3 | \ (f (x)\) ">\(f(3) = \vert 3 − 4\vert = \vert − 1\vert = 1\) |
| \ (x\) ">4 | \ (f (x)\) ">\(f(4) = \vert 4 − 4\vert = \vert 0\vert = 0\) |
| \ (x\) ">5 | \ (f (x)\) ">\(f(5) = \vert 5 − 4\vert = \vert 1\vert = 1\) |
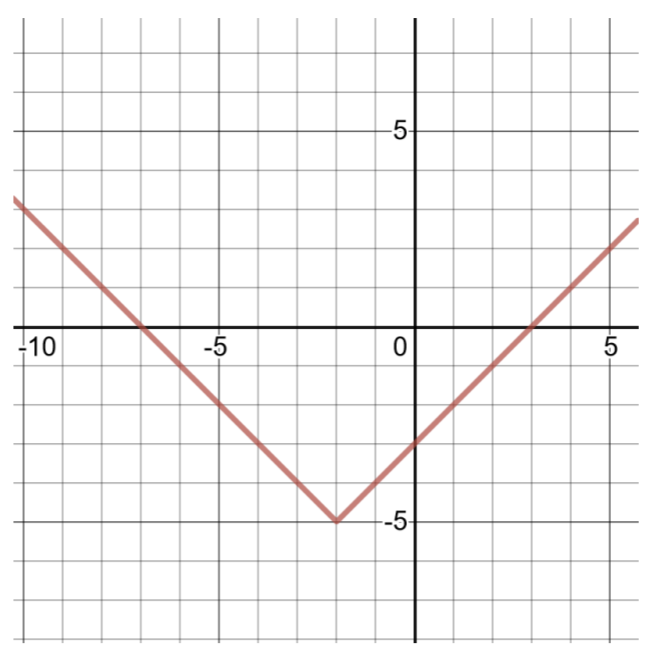
قم بإنشاء جدول للحلول ورسم دالة القيمة المطلقة التالية:
\(g(x) = \vert x + 2\vert − 5\)
الحل
مقارنة هذه الدالة بالشكل العام لوظائف القيمة المطلقة (كما هو موضح أعلاه)،\(a = 1\)،\(h = −2\)،\(k = −5\). قمة الرأس هي (h، k)\) أو\((−2, −5)\).
للعثور على زوجين آخرين مُرتَّبين، اختر\(x = −3\) قيم ثم قم بحسابها\(x = −1\)\(g(x)\)
Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.05:_وظائف_القيمة_المطلقة), /content/body/section[2]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(g(x) = \vert x + 2\vert − 5\) | |
| \(x\) | \(g(x)\) |
| -3 | \(g(−3) = \vert − 3 + 2\vert − 5 = \vert − 1\vert − 5 = 1 − 5 = −4\) |
| -2 | \(g(−2) = \vert − 2 + 2\vert − 5 = \vert 0\vert − 5 = 0 − 5 = −5\) |
| -1 | \(g(−1) = \vert − 1 + 2\vert − 5 = \vert 1\vert − 5 = 1 − 5 = −4\) |
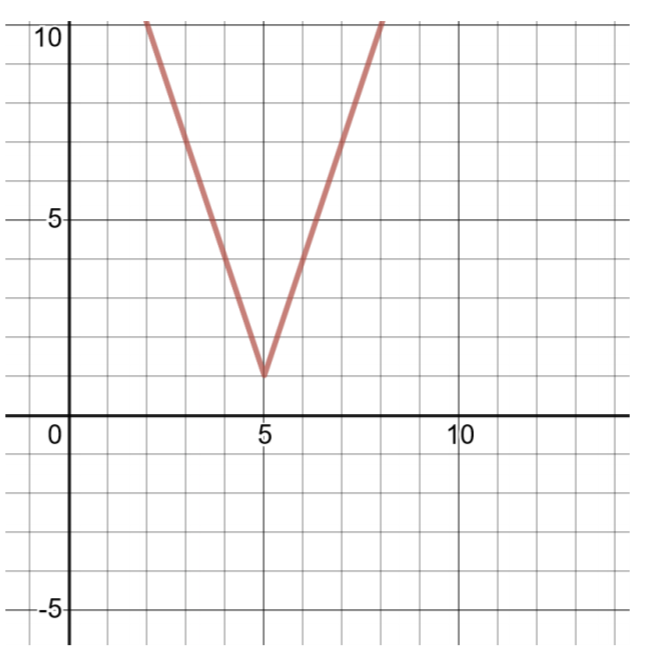
قم بإنشاء جدول للحلول ورسم دالة القيمة المطلقة التالية:
\(h(x) = 3\vert x − 5\vert + 1\)
الحل
مقارنة هذه الدالة بالشكل العام لوظائف القيمة المطلقة (كما هو موضح أعلاه)،\(a = 3\)،\(h = 5\)،\(k = 1\). قمة الرأس هي\((h, k)\) أو\((5, 1)\).
للعثور على زوجين آخرين مُرتَّبين، اختر\(x = 4\) قيم ثم قم بحسابها\(h(x)\).\(x = 6\)
Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.05:_وظائف_القيمة_المطلقة), /content/body/section[3]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(h(x) = 3\vert x − 5\vert + 1\) | |
| \(x\) | \(h(x)\) |
| 4 | \(g(−3) = \vert − 3 + 2\vert − 5 = \vert − 1\vert − 5 = 1 − 5 = −4\) |
| 5 | \(g(−2) = \vert − 2 + 2\vert − 5 = \vert 0\vert − 5 = 0 − 5 = −5\) |
| 6 | \(g(−1) = \vert − 1 + 2\vert − 5 = \vert 1\vert − 5 = 1 − 5 = −4\) |
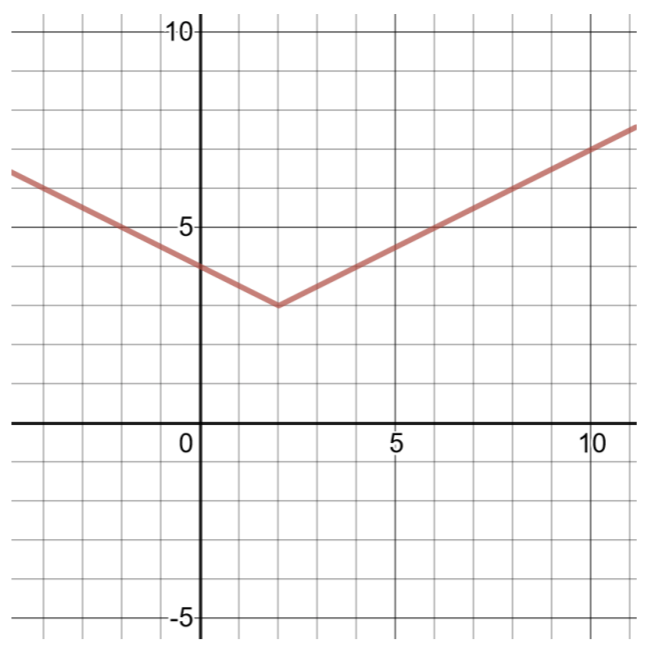
قم بإنشاء جدول للحلول ورسم دالة القيمة المطلقة التالية:
\(h(x) = \dfrac{1}{2} \vert x − 2\vert + 3\)
الحل
مقارنة هذه الدالة بالشكل العام لوظائف القيمة المطلقة (كما هو موضح أعلاه)،\(a = \dfrac{1}{2} \)،\(h = 2\)،\(k = 3\). قمة الرأس هي\((h, k)\) أو\((2, 3)\).
للعثور على زوجين آخرين مُرتَّبين، اختر\(x = 1\) قيم ثم قم بحسابها\(h(x)\).\(x = 3\)
Callstack:
at (اللغة_العربية/(__)/04:_الوظائف/4.05:_وظائف_القيمة_المطلقة), /content/body/section[4]/div/figure/figcaption/span, line 1, column 17
| جدول الحلول لـ\(h(x) = \dfrac{1}{2} \vert x − 2\vert + 3\) | |
| \(x\) | \(h(x)\) |
| 1 | \(h(1) = \dfrac{1}{2} \vert 1 − 2\vert + 3 = \dfrac{1}{2} \vert − 1\vert + 3 = \dfrac{1}{2} (1) + 3 = 3\dfrac{1}{2}\) |
| 2 | \(h(2) = \dfrac{1}{2} \vert 2 − 2\vert + 3 = \dfrac{1}{2} \vert 0\vert + 3 = 0 + 3 = 3\) |
| 3 | \(h(3) = \dfrac{1}{2} \vert 3 − 2\vert + 3 = \dfrac{1}{2} \vert 1\vert + 3 = \dfrac{1}{2} (1) + 3 = 3\dfrac{1}{2}\) |
قم بإنشاء جدول للحلول ورسم وظائف القيمة المطلقة التالية:
- \(f(x) = \vert x + 6\vert\)
- \(g(x) = \dfrac{1}{3} \vert x − 3\vert + 5\)
- \(h(x) = 4\vert x + 2\vert + 2\)
- \(f(x) = \vert x − 1\vert − 5\)


