Skip to main content
Global

4.4: الوظائف الخطية

  1. Last updated
  2. Save as PDF
  • Page ID
    167067

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    تعريف: دالة خطية

    الدالة الخطية هي دالة لها الشكل\(f(x) = mx+b\). أي سطر يمكن التعبير عنه في النموذج\(y = mx + b\) هو أيضًا وظيفة.

    استخدم تدوين الدالة عندما لا تحتوي معادلة الخط المكتوب بصيغة Slope-Intercipt على فجوات أو فواصل ولا يكون الخط خطًا رأسيًا. الدوال الخطية المكتوبة\(f(x) = mx + b\) كاجتياز اختبار الخط العمودي:

    تعريف: اختبار الخط العمودي

    يُستخدم اختبار الخط العمودي لتحديد ما إذا كان الرسم البياني يعرّف الإخراج الرأسي كدالة للإدخال الأفقي. إذا كان أي خط عمودي سيعبر الرسم البياني أكثر من مرة، فإن الرسم البياني لا يحدد مخرجًا رأسيًا واحدًا فقط لكل إدخال أفقي.

    لمزيد من المعلومات حول المعادلات الخطية، راجع قسم الخطوط المستقيمة.

    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[3]/header/div/h5/span/span, line 1, column 17

    قم بإنشاء جدول للحلول ورسم الوظائف الخطية التالية:

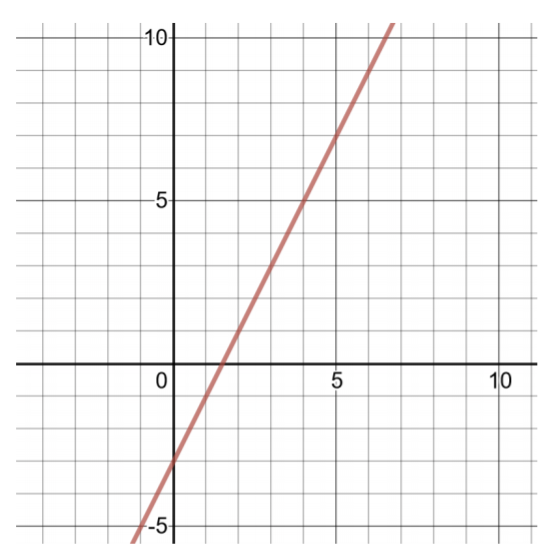
    \(f(x) = 2x − 3\)

    الحل

    \(f(x) = 2x − 3\)

    للعثور على زوجين مرتبين، اختر قيمًا صغيرة لـ\(x\)، ثم احسب قيم\(f(x)\).

    clipboard_e29fd85b9c181a1598af5c64e8ac834a9.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[3]/div/figure/figcaption/span, line 1, column 17
    جدول الحلول لـ\(f(x) = 2x − 3\)
    \(x\) \(f(x)\)
    -1 \(f(−1) = 2(−1) − 3 = −2 − 3 = −5\)
    0 \(f(0) = 2(0) − 3 = 0 − 3 = 3\)
    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[4]/header/div/h5/span/span, line 1, column 17

    قم بإنشاء جدول للحلول ورسم الدالة الخطية التالية:

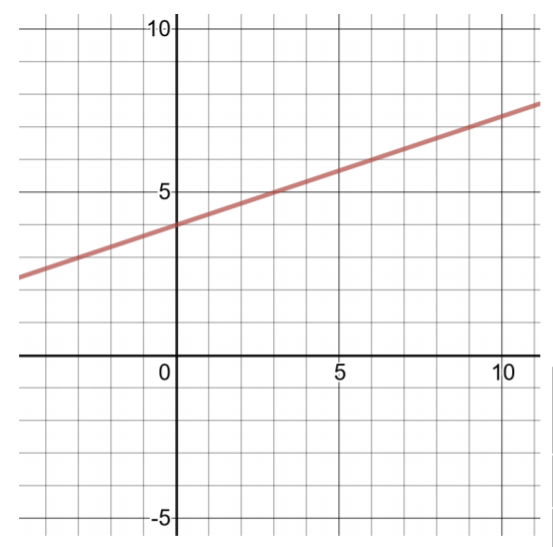
    \(g(x) = \dfrac{1}{ 3} x + 4\)

    الحل

    للعثور على زوجين مرتبين، اختر قيمًا صغيرة لـ x، ثم احسب قيم\(g(x)\). نظرًا لأن معامل المصطلح الذي يحتوي على x هو كسر، اختر مضاعفات المقام\(\dfrac{1 }{3} x\) حتى يكون حاصل الضرب عددًا صحيحًا.

    clipboard_ee79443c652fdf8b732b23ff5aa9bfefd.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[4]/div/figure/figcaption/span, line 1, column 17
    جدول الحلول لـ\(g(x) =\dfrac{ 1 }{3} x + 4\)
    \(x\) \(g(x)\)
    0 \(g(0) = \dfrac{1 }{3} (0) + 4 = 4\)
    3 \(g(3) = \dfrac{1 }{3} (3) + 4 = 1 + 4 = 5\)
    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[5]/header/div/h5/span/span, line 1, column 17

    قم بإنشاء جدول للحلول ورسم الوظائف الخطية التالية:

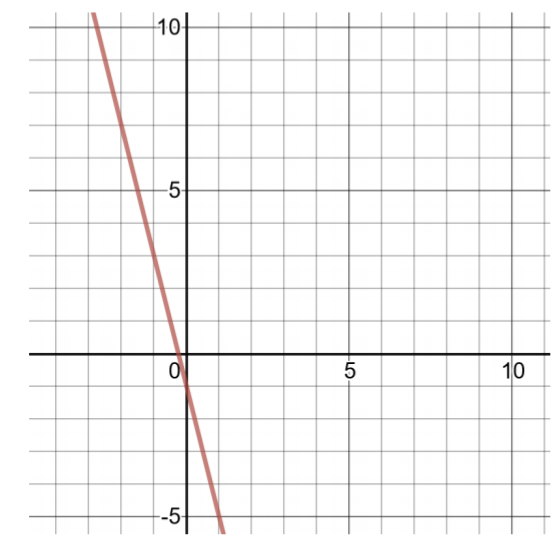
    \(h(x) = −4x − 1\)

    الحل

    للعثور على زوجين مرتبين، اختر قيمًا صغيرة لـ\(x\)، ثم احسب قيم\(h(x)\).

    clipboard_e9c1e072a5ba446060a941d3080d49668.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[5]/div/figure/figcaption/span, line 1, column 17
    جدول الحلول لـ\(h(x) = −4x − 1\)
    \(x\) \(h(x)\)
    0 \(h(0) = −4(0) − 1 = −1\)
    1 \(h(1) = −4(1) − 1 = −5\)
    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[6]/header/div/h5/span/span, line 1, column 17

    قم بإنشاء جدول للحلول ورسم الوظائف الخطية التالية:

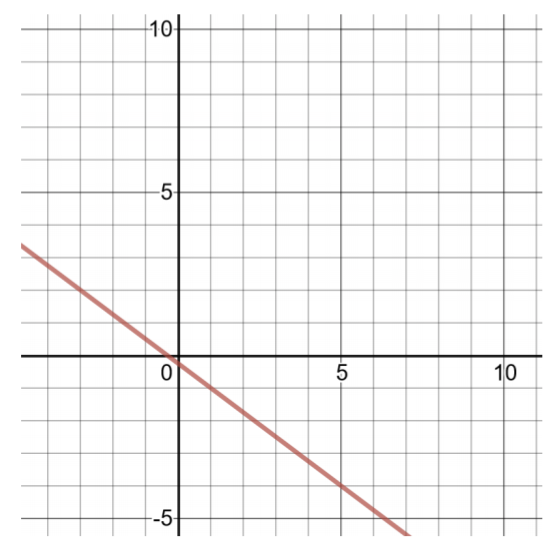
    \(h(x) = − \dfrac{3 }{4} x − \dfrac{1 }{4}\)

    الحل

    للعثور على زوجين مرتبين، اختر قيمًا صغيرة لـ\(x\)، ثم احسب قيم\(h(x)\) .نظرًا لأن معامل المصطلح المحتوي على\(x\) كسر، اختر مضاعفات المقام\(− \dfrac{3}{4} x\) حتى يكون حاصل الضرب عددًا صحيحًا.

    clipboard_eda0a4847b8349cd771ea227d008b6388.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[6]/div/figure/figcaption/span, line 1, column 17
    جدول الحلول لـ\(h(x) = − \dfrac{3}{4} x − \dfrac{1}{4}\)
    \(x\) \(h(x)\)
    0 \(h(0) = − \dfrac{3}{4} (0) − \dfrac{1}{4} = − \dfrac{1}{4}\)
    4 \(h(4) = − \dfrac{3}{4} (4) − \dfrac{1}{4} = −3 − \dfrac{1}{4} = −3 \dfrac{1}{4}\)
    التمرين
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/04:_الوظائف/4.04:_الوظائف_الخطية), /content/body/section[7]/header/div/h5/span/span, line 1, column 17

    قم بإنشاء جدول للحلول ورسم الوظائف الخطية التالية:

    1. \(f(x) = 4x − 9\)
    2. \(g(x) = \dfrac{1}{ 2} x − 2\)
    3. \(h(x) = −3x + 5\)
    4. \(f(x) = − \dfrac{2}{ 3} x −\dfrac{ 1 }{3}\)