B: أساسيات الرياضيات

Last updated
Save as PDF

Page ID: 195125

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

المربعات والقوى الأخرى

الأس، أو القوة، هو اختصار رياضي للمضاعفات المتكررة. على سبيل المثال، يعني الأس «2" ضرب قاعدة هذا الأس بنفسه (في المثال هنا، القاعدة هي «5"):

\[5^2=5×5=25\]

الأس هو «2" والقاعدة هي الرقم «5". هذا التعبير (ضرب الرقم في حد ذاته) يسمى أيضًا بالمربع. يتم تربيع أي رقم يتم رفعه إلى قوة 2. يتم تكعيب أي رقم يتم رفعه إلى قوة 3:

\[5^3=5×5×5=125\]

الرقم الذي يتم رفعه إلى القوة الرابعة يساوي هذا الرقم مضروبًا في نفسه أربع مرات، وهكذا بالنسبة للقوى العليا. بشكل عام:

\[n^x=n×n^{x−1}\]

حساب النسب المئوية

النسبة المئوية هي طريقة للتعبير عن كمية جزئية من شيء ما باستخدام وحدة كاملة مقسمة إلى 100 جزء. النسبة المئوية هي نسبة مقامها 100. نحن نستخدم رمز النسبة المئوية،%، لإظهار النسبة المئوية. وبالتالي، فإن 25٪ تعني نسبة\(\frac{25}{100}\)، و 3٪ تعني نسبة\(\frac{3}{100}\)، و 100٪ تعني\(\frac{100}{100}\)، أو الكل.

تحويل النسب المئوية

يمكن تحويل النسبة المئوية إلى كسر بكتابة قيمة النسبة المئوية ككسر بمقامه 100 وتبسيط الكسر إن أمكن.

\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]

يمكن تحويل النسبة المئوية إلى عدد عشري بكتابة قيمة النسبة المئوية في صورة كسر بمقامه 100 وقسمة البسط على المقام.

\[10\%=\dfrac{10}{100}=0.10\]

لتحويل عدد عشري إلى نسبة مئوية، اكتب العدد العشري في صورة كسر. إذا لم يكن مقام الكسر 100، فقم بتحويله إلى كسر مقامه 100، ثم اكتب الكسر كنسبة مئوية.

\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]

لتحويل كسر إلى نسبة مئوية، قم أولاً بتحويل الكسر إلى رقم عشري، ثم قم بتحويل العدد العشري إلى نسبة مئوية.

\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]

لنفترض أن باحثًا وجد أن 15 من أصل 23 طالبًا في الفصل يحملون النيسرية السحائية. ما النسبة المئوية للطلاب الذين يعملون كناقلين؟ للعثور على هذه القيمة، قم أولاً بالتعبير عن الأرقام في صورة كسر.

\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]

ثم قسّم البسط على المقام.

\[\dfrac{15}{23}=15\div 23 \approx 0.65\]

وأخيرًا، لتحويل عدد عشري إلى نسبة مئوية، اضرب في 100.

\[0.65 \times 100=65\%\]

النسبة المئوية للطلاب الذين يحملون ناقلات هي 65٪.

يمكنك أيضًا الحصول على بيانات عن الحدوث وعدم الحدوث؛ على سبيل المثال، في عينة من الطلاب، كانت نتيجة اختبار 9 إيجابية للأجسام المضادة للتوكسوبلازما، في حين كانت نتيجة اختبار 28 سلبية. ما هي النسبة المئوية للطلاب المصابين بفيروس نقص المناعة البشرية؟ الخطوة الأولى هي تحديد «الكل» الذي يشكل الطلاب الإيجابيون جزءًا منه. للقيام بذلك، قم بتجميع الاختبارات الإيجابية والسلبية.

\[\mathrm{positive+negative=9+28=37}\]

تألفت العينة بأكملها من 37 طالبًا. جزء الإيجابيات هو:

\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]

لإيجاد النسبة المئوية للطلاب الذين يحملون السلاح، قسّم البسط على المقام واضربه في 100.

\ [\ dfrac {9} {37} =9\ div 37\ حوالي 0.24\\
0.24\ مرات 100=24\%\]

تبلغ نسبة الطلاب الإيجابيين حوالي 24٪.

هناك طريقة أخرى للتفكير في حساب النسبة المئوية وهي إعداد كسور مكافئة، واحدة منها هي الكسر مع 100 كمقام، والضرب العرضي. سيتم التعبير عن المثال السابق على النحو التالي:

\[\dfrac{9}{37}=\dfrac{x}{100}\]

الآن، اضرب متقاطعًا وقم بحل المجهول:

\ [\ البدء {المحاذاة}
9\ مرات 100 &=37 x &\ nالرقم\\ [5pt]
\ frac {9\ مرات 100} {37} &=x &\ النص {قسّم كلا الجانبين على 37}\\ لا يوجد رقم\\ [5pt]
\ frac {900} {37} &=x &\ text {اضرب}\ بدون رقم\\ [5pt]
24\\\\ تقريباً x &\ text {تقسيم}\ بدون رقم
\ نهاية {محاذاة}\]

الإجابة، مدورة، هي نفسها.

الضرب والقسمة بالعشرات

في العديد من المجالات، وخاصة في العلوم، من الشائع ضرب الأعداد العشرية بقوى 10. دعونا نرى ما يحدث عندما نضرب 1.9436 ببعض قوى 10.

\ [\ ابدأ {المحاذاة}
1.9436 (10) &=19.436\ لا يوجد رقم\\
1.9436 (100) &=194.36\ بدون رقم\\
1.9436 (1000) &=1943.6\ لا يوجد رقم
\ نهاية {محاذاة}\]

عدد الأماكن التي تنقلها العلامة العشرية هو نفس عدد الأصفار بقوة عشرة. \(\PageIndex{1}\)يلخص الجدول النتائج.

طاولة\(\PageIndex{1}\)
اضرب في	الأصفار	تتحرك النقطة العشرية..
10	1	مكان واحد على اليمين
100	2	مكانين على اليمين
1,000	3	3 أماكن على اليمين
10,000	4	4 أماكن على اليمين

يمكننا استخدام هذا النمط كاختصار للضرب في قوى العدد عشرة بدلاً من الضرب باستخدام التنسيق الرأسي. يمكننا حساب الأصفار بقوة 10 ثم نقل العلامة العشرية التي تحتوي على نفس عدد الأماكن إلى اليمين.

لذلك، على سبيل المثال، لضرب 45.86 في 100، انقل العلامة العشرية مكانين إلى اليمين.

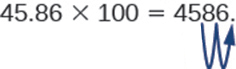
تقرأ المعادلة 45.86 × 100 = 4586. يُظهر سهم النقطة العشرية وهي تتحرك مكانين إلى اليمين.

في بعض الأحيان عندما نحتاج إلى نقل الفاصلة العشرية، لا توجد منازل عشرية كافية. في هذه الحالة، نستخدم الأصفار كعناصر نائبة. على سبيل المثال، دعونا نضرب 2.4 في 100. نحن بحاجة إلى نقل النقطة العشرية 2 إلى اليمين. نظرًا لوجود رقم واحد فقط على يمين العلامة العشرية، يجب أن نكتب 0 في خانة المئات.

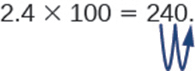
تقرأ المعادلة 2.4 × 100 = 240. يُظهر سهم النقطة العشرية وهي تتحرك مكانين إلى اليمين.

عند القسمة على قوى العدد ١٠، ما عليك سوى اتباع النهج المعاكس ونقل العدد العشري إلى اليسار بعدد الأصفار في قوة العشرة.

دعونا نرى ما يحدث عندما نقسم 1.9436 على بعض قوى 10.

\ [\ ابدأ {المحاذاة}
1.9436\ div 10 &=0.19436\ لا يوجد رقم\\
1.9436\ div 100&=0.019436\ بدون رقم\\\
1.9436\ div 1000&=0.0019436\ لا يوجد رقم
\ نهاية {محاذاة}\]

في حالة عدم وجود أرقام كافية لنقل الرقم العشري، قم بإضافة الأصفار لإنشاء الأماكن.

الترميز العلمي

يتم استخدام الترميز العلمي للتعبير عن الأرقام الكبيرة جدًا والصغيرة جدًا كمنتج لرقمين. عادةً ما يكون الرقم الأول للمنتج، وهو المصطلح الرقمي، رقمًا لا يقل عن 1 ولا يزيد عن 10. يُكتب الرقم الثاني للمنتج، وهو الحد الأسي، في صورة 10 باستخدام الأس. يتم إعطاء بعض الأمثلة على الترميز العلمي في الجدول\(\PageIndex{2}\).

طاولة\(\PageIndex{2}\)
الترميز القياسي	الترميز العلمي
1000	1 × 10 ³
100	1 × 10 ²
10	1 × 10 ¹
1	1 × 10 ⁰
0.1	1 × 10 ⁻¹
0.01	1 × 10 ⁻²

يُعد الترميز العلمي ترميزًا مفيدًا بشكل خاص للأعداد الكبيرة جدًا والصغيرة جدًا، مثل 1,230,000,000 = 1.23 × 10 ⁹، و0.00000000036 = 3.6 × 10 ⁻¹⁰.

التعبير عن الأرقام في الترميز العلمي

يعد تحويل أي رقم إلى تدوين علمي أمرًا سهلاً. احسب عدد الأماكن اللازمة لنقل الرقم العشري بجوار الرقم الموجود في أقصى اليسار من غير الصفر: أي لجعل الرقم بين 1 و10. ثم اضرب هذا الرقم في 10 مرفوعًا إلى عدد الأماكن التي نقلت فيها الرقم العشري. يكون الأس موجبًا إذا قمت بنقل العلامة العشرية إلى اليسار والسالبة إذا قمت بنقل العلامة العشرية إلى اليمين. لذا

\[2386=2.386\times1000=2.386\times10^3\]

\[0.123=1.23\times0.1=1.23\times10^{-1}\]

القوة (الأس) لـ 10 تساوي عدد الأماكن التي يتم فيها تغيير الرقم العشري.

اللوغاريتمات

اللوغاريتم المشترك (اللوغاريتم) للرقم هو القوة التي يجب رفع 10 إليها لتساوي هذا الرقم. على سبيل المثال، اللوغاريتم الشائع لـ 100 هو 2، لأنه يجب رفع 10 إلى القوة الثانية لتساوي 100. توجد أمثلة إضافية في الجدول\(\PageIndex{3}\).

طاولة\(\PageIndex{3}\)
رقم	الشكل الأسي	اللوغاريتم المشترك
1000	10 ³	3
10	10 ¹	1
1	10 ⁰	0
0.1	10 ⁻¹	−1
0.001	10 ⁻³	−3

للعثور على اللوغاريتم الشائع لمعظم الأرقام، ستحتاج إلى استخدام زر LOG على الآلة الحاسبة.

التقريب والأرقام الهامة

عند الإبلاغ عن البيانات الرقمية التي تم الحصول عليها من خلال القياسات، نستخدم فقط العديد من الأرقام المهمة التي تتطلبها دقة القياس. على سبيل المثال، لنفترض أن عالم الأحياء الدقيقة الذي يستخدم عداد الخلايا الآلي يحدد وجود 525341 خلية بكتيرية في عينة سعة لتر واحد من مياه النهر. ومع ذلك، فإنها تسجل التركيز على أنه 525,000 خلية لكل لتر وتستخدم هذا الرقم المستدير لتقدير عدد الخلايا التي من المحتمل أن توجد في 10 لترات من مياه النهر. في هذه الحالة، لا تعتبر الأرقام الثلاثة الأخيرة من الكمية المقاسة مهمة. يتم تقريبها لحساب الاختلافات في عدد الخلايا التي من المحتمل أن تحدث إذا تم قياس المزيد من العينات.

تكمن أهمية الأرقام المهمة في تطبيقها على الحساب الأساسي. بالإضافة إلى الجمع والطرح، يجب أن يحتوي المجموع أو الفرق على أكبر عدد من الأرقام على يمين العلامة العشرية كما هو الحال في الأرقام الأقل تحديدًا (المشار إليها بالتسطير في المثال التالي) للأرقام المستخدمة في الحساب.

لنفترض أن عالم الأحياء الدقيقة يرغب في حساب الكتلة الإجمالية لعينتين من الأجار.

\ [\ ابدأ {مصفوفة} {l}
4.38\ تسطير تحت الخط {3}\\ النص {g}\
\\ تسطير {3.002\ تسطير {1}\\ النص {g}\\
7.38\ تسطير {5}\ النص {g}
\ النهاية {المصفوفة}\]

يحتوي الحد الأدنى من الكتلتين على ثلاث منازل عشرية، لذلك يجب أن يحتوي المجموع على ثلاث منازل عشرية.

في الضرب والقسمة، يجب ألا يحتوي المنتج أو حاصل القسمة على أرقام أكثر من العامل الذي يحتوي على أقل عدد من الأرقام الهامة. لنفترض أن عالم الأحياء الدقيقة يرغب في حساب مقدار الكاشف الذي سيكون موجودًا في 6.6 مل إذا كان التركيز 0.638 جم/مل.

\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]

مرة أخرى، تحتوي الإجابة على منزلة عشرية واحدة فقط لأن هذه هي دقة الرقم الأقل دقة في الحساب.

عند تقريب الأرقام، قم بزيادة الرقم المحتفظ به بمقدار 1 إذا كان متبوعًا برقم أكبر من 5 («التقريب»). لا تقم بتغيير الرقم الذي تم الاحتفاظ به إذا كانت الأرقام التالية أقل من 5 («التقريب»). إذا كان الرقم المحتفظ به متبوعًا بـ 5، فقم بالتقريب إذا كان الرقم المحتفظ به فرديًا، أو تقريبه لأسفل إذا كان زوجيًا (بعد التقريب، سيكون الرقم المحتفظ به دائمًا زوجيًا).

وقت الجيل

من الممكن كتابة معادلة لحساب أرقام الخلايا في أي وقت إذا كان عدد خلايا البداية ووقت المضاعفة معروفين، طالما أن الخلايا تنقسم بمعدل ثابت. نحدد N ₀ كرقم البداية للبكتيريا، الرقم في الوقت t = 0. N _i هو عدد البكتيريا في الوقت t = i، وهو وقت تعسفي في المستقبل. أخيرًا، سنحدد j مساويًا لعدد الأجيال، أو عدد المرات التي يتضاعف فيها عدد الخلايا خلال الفترة الزمنية. ثم لدينا،

\[N_i=N_0\times2^j\]

هذه المعادلة هي تعبير عن النمو بالانشطار الثنائي.

في مثالنا، N ₀ = 4، عدد الأجيال، j، يساوي 3 بعد 90 دقيقة لأن وقت الجيل هو 30 دقيقة. يمكن تقدير عدد الخلايا من المعادلة التالية:

\ [\ ابدأ {المحاذاة}
n_i&=n_0\ times2^j\ لا يوجد رقم\\\
N_ {90} &=4\ مرات 2^3\ بدون رقم\\
N_ {90} &=4\ مرات 8=32\ لا يوجد رقم
\ نهاية {محاذاة}\]

عدد الخلايا بعد 90 دقيقة هو 32.

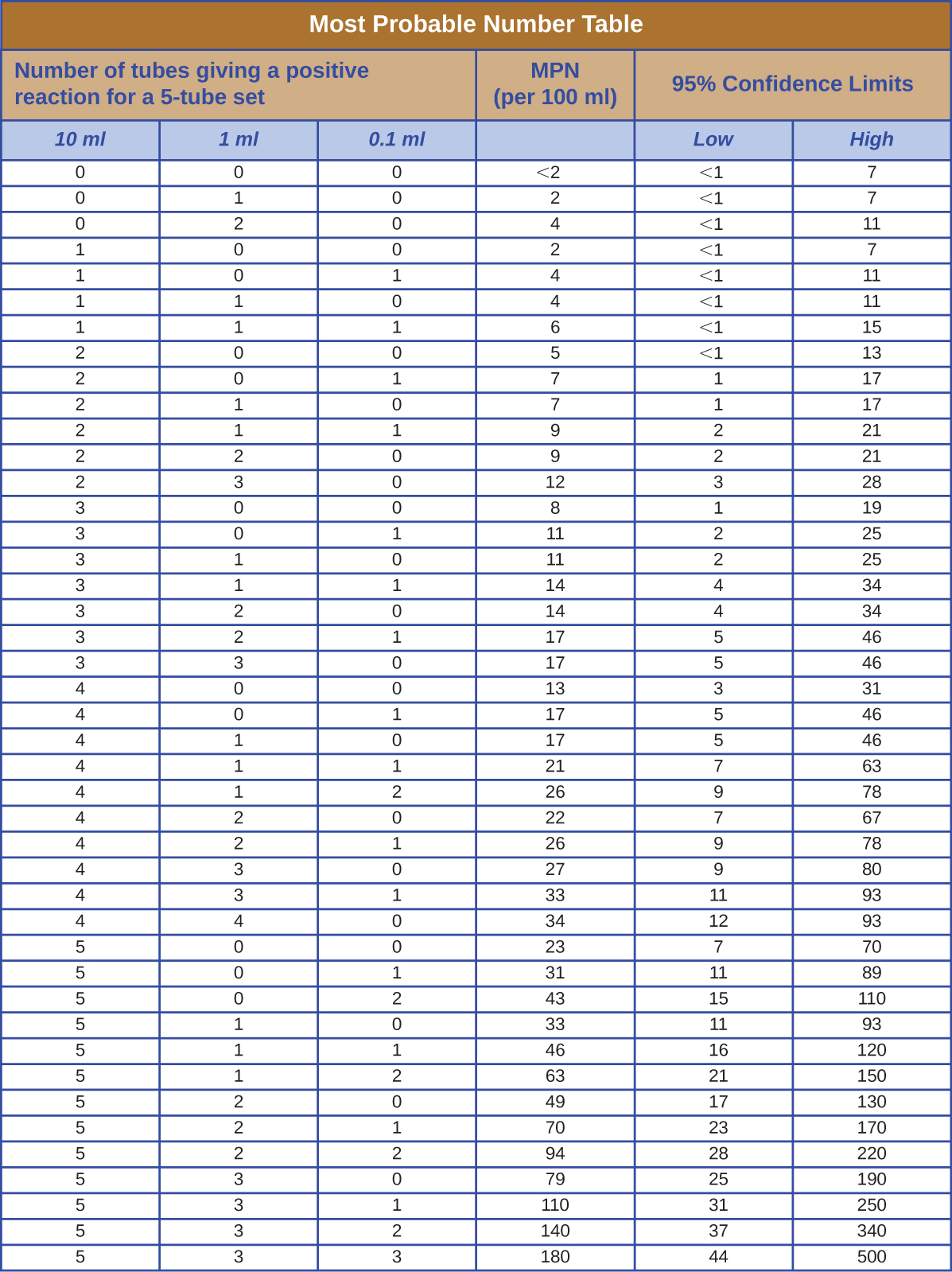
الرقم الأكثر احتمالاً

\(\PageIndex{1}\)يحتوي الجدول في الشكل على القيم المستخدمة لحساب المثال العددي الأكثر احتمالاً الوارد في كيفية نمو الميكروبات.

يوجد جدول بعنوان جدول الأرقام الأكثر احتمالاً. لكل صف، يوضح عدد الأنابيب التي تعطي تفاعلًا إيجابيًا لمجموعة من 5 أنابيب لـ 10 مل و 1 مل و 0.1 مل، تليها MPN لكل 100 مل، وحدود الثقة بنسبة 95٪ للأنابيب المنخفضة والعالية. بالنسبة للصف 1، تكون التفاعلات 10 مل = 0، 1 مل = 0، 0.1 مل = 0؛ MPN هي <2، وحدود الثقة المنخفضة والعالية هي <1 و 7. بالنسبة للصف 2، تكون التفاعلات 10 مل = 0، 1 مل = 1، 0.1 مل = 0؛ MPN هي 2، وحدود الثقة المنخفضة والعالية هي <1 و 7. بالنسبة للصف 3، تكون التفاعلات 10 مل = 0، 1 مل = 2، 0.1 مل = 0؛ MPN هي 4، وحدود الثقة المنخفضة والعالية هي <1 و 11. بالنسبة للصف 4، تكون التفاعلات 10 مل = 1، 1 مل = 0، 0.1 مل = 0؛ MPN هي 2، وحدود الثقة المنخفضة والعالية هي <1 و 7. بالنسبة للصف 5، تكون التفاعلات 10 مل = 1، 1 مل = 0، 0.1 مل = 1؛ MPN هي 4، وحدود الثقة المنخفضة والعالية هي <1 و 11. بالنسبة للصف 6، تكون التفاعلات 10 مل = 1، 1 مل = 1، 0.1 مل = 0؛ MPN هي 4، وحدود الثقة المنخفضة والعالية هي <1 و 11. بالنسبة للصف 7، تكون التفاعلات 10 مل = 1، 1 مل = 1، 0.1 مل = 1؛ MPN هي 6، وحدود الثقة المنخفضة والعالية هي <1 و 15. بالنسبة للصف 8، تكون التفاعلات 10 مل = 2، 1 مل = 0، 0.1 مل = 0؛ MPN هي 5، وحدود الثقة المنخفضة والعالية هي <1 و 13. بالنسبة للصف 9، تكون التفاعلات 10 مل = 2، 1 مل = 0، 0.1 مل = 1؛ MPN هي 7، وحدود الثقة المنخفضة والعالية هي 1 و 17. بالنسبة للصف 10، تكون التفاعلات 10 مل = 2، 1 مل = 1، 0.1 مل = 0؛ MPN هي 7، وحدود الثقة المنخفضة والعالية هي 1 و 17. بالنسبة للصف 11، تكون التفاعلات 10 مل = 2، 1 مل = 1، 0.1 مل = 1؛ MPN هي 9، وحدود الثقة المنخفضة والعالية هي 2 و 21. بالنسبة للصف 12، تكون التفاعلات 10 مل = 2، 1 مل = 2، 0.1 مل = 0؛ MPN هي 9، وحدود الثقة المنخفضة والعالية هي 2 و 21. بالنسبة للصف 13، تكون التفاعلات 10 مل = 2، 1 مل = 3، 0.1 مل = 0؛ MPN هي 12، وحدود الثقة المنخفضة والعالية هي 3 و 28. بالنسبة للصف 14، تكون التفاعلات 10 مل = 3، 1 مل = 0، 0.1 مل = 0؛ MPN هي 8، وحدود الثقة المنخفضة والعالية هي 1 و 19. بالنسبة للصف 15، تكون التفاعلات 10 مل = 3، 1 مل = 0، 0.1 مل = 1؛ MPN هي 11، وحدود الثقة المنخفضة والعالية هي 2 و 25. بالنسبة للصف 16، تكون التفاعلات 10 مل = 3، 1 مل = 1، 0.1 مل = 0؛ MPN هي 11، وحدود الثقة المنخفضة والعالية هي 2 و 25. بالنسبة للصف 17، تكون التفاعلات 10 مل = 3، 1 مل = 1، 0.1 مل = 1؛ MPN هي 14، وحدود الثقة المنخفضة والعالية هي 4 و 34. بالنسبة للصف 18، تكون التفاعلات 10 مل = 3، 1 مل = 2، 0.1 مل = 0؛ MPN هي 14، وحدود الثقة المنخفضة والعالية هي 4 و 34. بالنسبة للصف 19، تكون التفاعلات 10 مل = 3، 1 مل = 2، 0.1 مل = 1؛ MPN هي 17، وحدود الثقة المنخفضة والعالية هي 5 و 46. بالنسبة للصف 20، تكون التفاعلات 10 مل = 3، 1 مل = 3، 0.1 مل = 0؛ MPN هي 17، وحدود الثقة المنخفضة والعالية هي 5 و 46. بالنسبة للصف 21، تكون التفاعلات 10 مل = 4، 1 مل = 0، 0.1 مل = 0؛ MPN هي 13، وحدود الثقة المنخفضة والعالية هي 3 و 31. بالنسبة للصف 22، تكون التفاعلات 10 مل = 4، 1 مل = 0، 0.1 مل = 1؛ MPN هي 17، وحدود الثقة المنخفضة والعالية هي 5 و 46. بالنسبة للصف 23، تكون التفاعلات 10 مل = 4، 1 مل = 1، 0.1 مل = 0؛ MPN هي 17، وحدود الثقة المنخفضة والعالية هي 5 و 46. بالنسبة للصف 24، تكون التفاعلات 10 مل = 4، 1 مل = 1، 0.1 مل = 1؛ MPN هي 21، وحدود الثقة المنخفضة والعالية هي 7 و 63. بالنسبة للصف 25، تكون التفاعلات 10 مل = 4، 1 مل = 1، 0.1 مل = 2؛ MPN هي 26، وحدود الثقة المنخفضة والعالية هي 9 و 78. بالنسبة للصف 26، تكون التفاعلات 10 مل = 4، 1 مل = 2، 0.1 مل = 0؛ MPN هي 22، وحدود الثقة المنخفضة والعالية هي 7 و 67. بالنسبة للصف 27، تكون التفاعلات 10 مل = 4، 1 مل = 2، 0.1 مل = 1؛ MPN هي 26، وحدود الثقة المنخفضة والعالية هي 9 و 80. بالنسبة للصف 28، تكون التفاعلات 10 مل = 4، 1 مل = 3، 0.1 مل = 0؛ MPN هي 27، وحدود الثقة المنخفضة والعالية هي 9 و 80. بالنسبة للصف 29، تكون التفاعلات 10 مل = 4، 1 مل = 3، 0.1 مل = 1؛ MPN هي 33، وحدود الثقة المنخفضة والعالية هي 11 و 93. بالنسبة للصف 30، تكون التفاعلات 10 مل = 4، 1 مل = 4، 0.1 مل = 0؛ MPN هي 34، وحدود الثقة المنخفضة والعالية هي 12 و 93. بالنسبة للصف 31، تكون التفاعلات 10 مل = 5، 1 مل = 0، 0.1 مل = 0؛ MPN هي 23، وحدود الثقة المنخفضة والعالية هي 7 و 70. بالنسبة للصف 32، تكون التفاعلات 10 مل = 5، 1 مل = 0، 0.1 مل = 1؛ MPN هي 31، وحدود الثقة المنخفضة والعالية هي 11 و 89. بالنسبة للصف 33، تكون التفاعلات 10 مل = 5، 1 مل = 0، 0.1 مل = 2؛ MPN هي 43، وحدود الثقة المنخفضة والعالية هي 15 و 110. بالنسبة للصف 34، تكون التفاعلات 10 مل = 5، 1 مل = 1، 0.1 مل = 0؛ MPN هي 33، وحدود الثقة المنخفضة والعالية هي 11 و 93. بالنسبة للصف 35، تكون التفاعلات 10 مل = 5، 1 مل = 1، 0.1 مل = 1؛ MPN هي 46، وحدود الثقة المنخفضة والعالية هي 16 و 120. بالنسبة للصف 36، تكون التفاعلات 10 مل = 5، 1 مل = 1، 0.1 مل = 2؛ MPN هي 63، وحدود الثقة المنخفضة والعالية هي 21 و 150. بالنسبة للصف 37، تكون التفاعلات 10 مل = 5، 1 مل = 2، 0.1 مل = 0؛ MPN هي 49، وحدود الثقة المنخفضة والعالية هي 17 و 130. بالنسبة للصف 38، تكون التفاعلات 10 مل = 5، 1 مل = 2، 0.1 مل = 1؛ MPN هي 70، وحدود الثقة المنخفضة والعالية هي 23 و 170. بالنسبة للصف 39، تكون التفاعلات 10 مل = 5، 1 مل = 2، 0.1 مل = 2؛ MPN هي 94، وحدود الثقة المنخفضة والعالية هي 28 و 220. بالنسبة للصف 40، تكون التفاعلات 10 مل = 5، 1 مل = 3، 0.1 مل = 0؛ MPN هي 79، وحدود الثقة المنخفضة والعالية هي 25 و 190. بالنسبة للصف 41، تكون التفاعلات 10 مل = 5، 1 مل = 3، 0.1 مل = 1؛ MPN هي 110، وحدود الثقة المنخفضة والعالية هي 31 و 250. بالنسبة للصف 42، تكون التفاعلات 10 مل = 5، 1 مل = 3، 0.1 مل = 2؛ MPN هي 140، وحدود الثقة المنخفضة والعالية هي 37 و 340. بالنسبة للصف 43، تكون التفاعلات 10 مل = 5، 1 مل = 3، 0.1 مل = 3؛ MPN هي 180، وحدود الثقة المنخفضة والعالية هي 44 و 500. — الشكل\(\PageIndex{1}\)