9.6: حل المعادلات ذات الجذور التربيعية
- Page ID
- 200153
في نهاية هذا القسم، ستكون قادرًا على:
- حل المعادلات الجذرية
- استخدم الجذور التربيعية في التطبيقات
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- تبسيط: ⓐ\(\sqrt{9}\) ⓑ\(9^2\).
إذا فاتتك هذه المشكلة، راجع المثال 9.1.1 والتمرين 1.3.22. - حل: 5 (x+1) −4=3 (2x−7).
إذا فاتتك هذه المشكلة، راجع التمرين 2.4.16. - حل:\(n^2−6n+8=0\).
إذا فاتتك هذه المشكلة، راجع التمرين 7.6.13.
حل المعادلات الجذرية
في هذا القسم سوف نحل المعادلات التي تحتوي على المتغير في جذر التربيعي. تسمى المعادلات من هذا النوع المعادلات الجذرية.
المعادلة التي يكون فيها المتغير في جذر الجذر التربيعي تسمى المعادلة الجذرية.
كالعادة، عند حل هذه المعادلات، ما نفعله بأحد طرفي المعادلة يجب أن نفعله بالجانب الآخر أيضًا. نظرًا لأن تربيع الكمية وأخذ الجذر التربيعي هما عمليتان «معاكستان»، فسنقوم بتربيع كلا الجانبين لإزالة العلامة الجذرية وحل المتغير الموجود بالداخل.
ولكن تذكر أننا عندما نكتب\(\sqrt{a}\) نعني الجذر التربيعي الرئيسي. لذلك\(\sqrt{a} \ge 0\) دائمًا. عندما نحل المعادلات الجذرية عن طريق تربيع كلا الطرفين، قد نحصل على حل جبري يجعل النتيجة\(\sqrt{a}\) سالبة. لن يكون هذا الحل الجبري حلاً للمعادلة الجذرية الأصلية؛ إنه حل خارجي. لقد رأينا حلولًا غريبة عندما قمنا بحل المعادلات العقلانية أيضًا.
بالنسبة للمعادلة\(\sqrt{x+2}=x\):
- هل x=2 حل؟
- هل x=−1 حل؟
- إجابة
-
1. هل x=2 حل؟
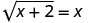
دعونا س = 2. 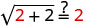
قم بالتبسيط. 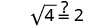
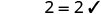
2 هو الحل. 2. هل x=−1 حل؟
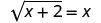
دعونا س = −1. 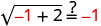
قم بالتبسيط. 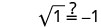
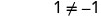
−1 ليس حلاً. −1 هو حل خارجي للمعادلة.
بالنسبة للمعادلة\(\sqrt{x+6}=x\):
- هل x=−2 حل؟
- هل x=3 حل؟
- إجابة
-
- كلا
- نعم
بالنسبة للمعادلة\(\sqrt{−x+2}=x\):
- هل x=−2 حل؟
- هل x=1 حل؟
- إجابة
-
- كلا
- نعم
من أجل\(a \ge 0\)،\((\sqrt{a})^2=a\)
كيفية حل المعادلات الجذرية
حل:\(\sqrt{2x−1}=7\)
- إجابة
-
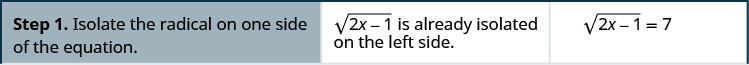



حل:\(\sqrt{3x−5}=5\).
- إجابة
-
10
حل:\(\sqrt{4x+8}=6\).
- إجابة
-
7
- اعزل الجذر على أحد طرفي المعادلة.
- قم بمربع طرفي المعادلة.
- حل المعادلة الجديدة.
- تحقق من الإجابة.
حل:\(\sqrt{5n−4}−9=0\).
- إجابة
-
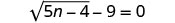
لعزل الراديكالي، أضف 9 إلى كلا الجانبين. 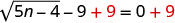
قم بالتبسيط. 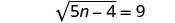
قم بمربع طرفي المعادلة. 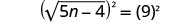
حل المعادلة الجديدة. 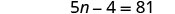


تحقق من الإجابة.

الحل هو n = 17.
حل:\(\sqrt{3m+2}−5=0\).
- إجابة
-
\(\frac{23}{3}\)
حل:\(\sqrt{10z+1}−2=0\).
- إجابة
-
\(\frac{3}{10}\)
حل:\(\sqrt{3y+5}+2=5\).
- إجابة
-
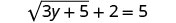
لعزل الجذر، اطرح 2 من كلا الجانبين. 
قم بالتبسيط. 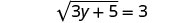
قم بمربع طرفي المعادلة. 
حل المعادلة الجديدة. 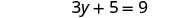

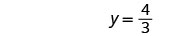
تحقق من الإجابة.
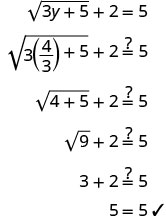
الحل هو\(y=\frac{4}{3}\)
حل:\(\sqrt{3p+3}+3=5\).
- إجابة
-
\(\frac{1}{3}\)
حل:\(\sqrt{5q+1}+4=6\).
- إجابة
-
\(\frac{3}{5}\)
عندما نستخدم علامة جذرية، فإننا نعني الجذر الرئيسي أو الإيجابي. إذا كانت المعادلة تحتوي على جذر تربيعي يساوي عددًا سالبًا، فلن يكون لهذه المعادلة أي حل.
حل:\(\sqrt{9k−2}+1=0\).
- إجابة
-
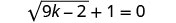
لعزل الجذر، اطرح 1 من كلا الجانبين. 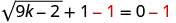
قم بالتبسيط. 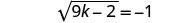
بما أن الجذر التربيعي يساوي رقمًا سالبًا، فلا يوجد حل للمعادلة.
حل:\(\sqrt{2r−3}+5=0\)
- إجابة
-
لا يوجد حل
حل:\(\sqrt{7s−3}+2=0\).
- إجابة
-
لا يوجد حل
\[\begin{array}{cc} {(a+b)^2=a^2+2ab+b^2}&{(a−b)^2=a^2−2ab+b^2}\\ \nonumber \end{array}\]
لا تنس المدى المتوسط!
حل:\(\sqrt{p−1}+1=p\).
- إجابة
-
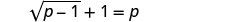
لعزل الجذر، اطرح 1 من كلا الجانبين. 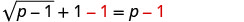
قم بالتبسيط. 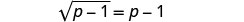
قم بمربع طرفي المعادلة. 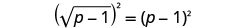
قم بتبسيط المعادلة الجديدة ثم حلها. 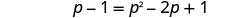
إنها معادلة تربيعية، لذا احصل على صفر على أحد الجانبين. 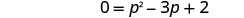
ضع الجانب الأيمن في الاعتبار. 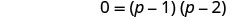
استخدم خاصية المنتج الصفري. 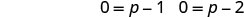
حل كل معادلة. 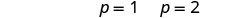
تحقق من الإجابات.
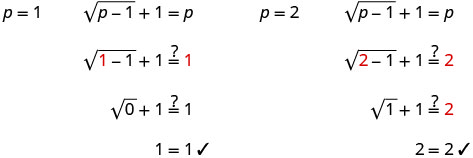
الحلول هي p = 1، p = 2.
حل:\(\sqrt{x−2}+2=x\).
- إجابة
-
2، 3
حل:\(\sqrt{y−5}+5=y\).
- إجابة
-
5، 6
حل:\(\sqrt{r+4}−r+2=0\).
- إجابة
-
\(\sqrt{r+4}−r+2=0\) اعزل الراديكالي. \(\sqrt{r+4}=r−2\) قم بمربع طرفي المعادلة. \((\sqrt{r+4})^2=(r−2)^2\) حل المعادلة الجديدة. \(r+4=r^2−4r+4\) إنها معادلة تربيعية، لذا احصل على صفر على أحد الجانبين. \(0=r^2−5r\) ضع الجانب الأيمن في الاعتبار. \(0=r(r−5)\) استخدم خاصية المنتج الصفري. 0=r 0=r−5 حل المعادلة. r=0 r=5 تحقق من الإجابة.
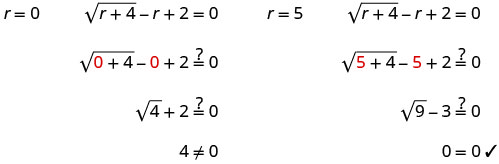
r=5 r=0 هو حل خارجي.
حل:\(\sqrt{m+9}−m+3=0\).
- إجابة
-
7
حل:\(\sqrt{n+1}−n+1=0\)
- إجابة
-
3
عندما يكون هناك معامل أمام الراديكالي، يجب علينا تربيعه أيضًا.
حل:\(3\sqrt{3x−5}−8=4\).
- إجابة
-
\(3\sqrt{3x−5}−8=4\) اعزل الراديكالي. \(3\sqrt{3x−5}=12\) قم بمربع طرفي المعادلة. \((3\sqrt{3x−5})^2=(12)^2\) قم بتبسيط المعادلة الجديدة ثم حلها. 9 (3x−5) = 14 قم بالتوزيع. 27×−45=144 حل المعادلة. 27 × = 189 س = 7 تحقق من الإجابة.
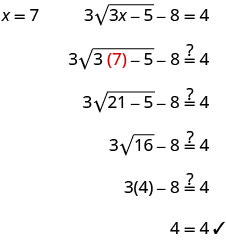
الحل هو x=7.
حل:\(\sqrt{24a+2}−16=16\).
- إجابة
-
\(\frac{127}{2}\)
حل:\(\sqrt{36b+3}−25=50\).
- إجابة
-
\(\frac{311}{3}\)
حل:\(\sqrt{4z−3}=\sqrt{3z+2}\).
- إجابة
-
\(\sqrt{4z−3}=\sqrt{3z+2}\) يتم عزل المصطلحات الراديكالية \(\sqrt{4z−3}=\sqrt{3z+2}\) قم بمربع طرفي المعادلة. \((\sqrt{4z−3})^2=(\sqrt{3z+2})^2\) قم بتبسيط المعادلة الجديدة ثم حلها 4z−3=3z+2 z−3=2 z = 5 س = 7 تحقق من الإجابة.
نترك الأمر لك لإظهار تلك الشيكات الخمسة!
الحل هو z=5.
حل:\(\sqrt{2x−5}=\sqrt{5x+3}\).
- إجابة
-
لا يوجد حل
حل:\(\sqrt{7y+1}=\sqrt{2y−5}\).
- إجابة
-
لا يوجد حل
في بعض الأحيان بعد تسوية طرفي المعادلة، لا يزال لدينا متغير داخل الجذر. عندما يحدث ذلك، نكرر الخطوة 1 والخطوة 2 من الإجراء الخاص بنا. نعزل الجذر والمربع على جانبي المعادلة مرة أخرى.
حل:\(\sqrt{m}+1=\sqrt{m+9}\).
- إجابة
-
\(\sqrt{m}+1=\sqrt{m+9}\) يتم عزل الراديكالي على الجانب الأيمن.
مربع على كلا الجانبين
\((\sqrt{m}+1)^2=(\sqrt{m+9})^2\) التبسيط - كن حذرًا جدًا أثناء التكاثر! \(m+2\sqrt{m}+1=m+9\) لا يزال هناك جذر جذري في المعادلة.
لذلك يجب علينا تكرار الخطوات السابقة. اعزل الراديكالي.
\(2\sqrt{m}=8\) قم بمربع كلا الجانبين. \((2\sqrt{m})^2=(8)^2\) قم بتبسيط المعادلة الجديدة ثم حلها. 4 م = 64 م = 16 تحقق من الإجابة.
نترك الأمر لك لإظهار أن m=16 شيكًا!
الحل هو m=16.
حل:\(\sqrt{x}+3=\sqrt{x+5}\).
- إجابة
-
لا يوجد حل
حل:\(\sqrt{m}+5=\sqrt{m+16}\).
- إجابة
-
لا يوجد حل
حل:\(\sqrt{q−2}+3=\sqrt{4q+1}\).
- إجابة
-
\(\sqrt{q−2}+3=\sqrt{4q+1}\) يتم عزل الراديكالي على الجانب الأيمن.
مربع على كلا الجانبين
\((\sqrt{q−2}+3)^2=(\sqrt{4q+1})^2\) قم بالتبسيط. \(q−2+6\sqrt{q−2}+9=4q+1\) لا يزال هناك جذر جذري في المعادلة.
لذلك يجب علينا تكرار الخطوات السابقة. اعزل الراديكالي.
\(6\sqrt{q−2}=3q−6\) قم بمربع كلا الجانبين. \((6\sqrt{q−2})^2=(3q−6)^2\) قم بتبسيط المعادلة الجديدة ثم حلها. \(36(q−2)=9q^2−36q+36\) قم بالتوزيع. \(36q−72=9q^2−36q+36\) إنها معادلة تربيعية، لذا احصل على صفر على أحد الجانبين. \(0=9q^2−72q+108\) ضع الجانب الأيمن في الاعتبار. \(0=9(q^2−8q+12)\)
\(0=9(q−6)(q−2)\)
استخدم خاصية المنتج الصفري \[\begin{array}{ll} {q−6=0}&{q−2=0}\\ {q=6}&{q=2}\\ \nonumber \end{array}\] الشيكات متروكة لك. (يجب أن يعمل كلا الحلين.)
الحلول هي q=6 و q=2.
حل:\(\sqrt{y−3}+2=\sqrt{4y+2}\).
- إجابة
-
لا يوجد حل
حل:\(\sqrt{n−4}+5=\sqrt{3n+3}\).
- إجابة
-
لا يوجد حل
استخدم الجذور المربعة في التطبيقات
أثناء تقدمك في دورات الكلية، ستواجه صيغًا تتضمن جذورًا مربعة في العديد من التخصصات. لقد استخدمنا بالفعل الصيغ لحل تطبيقات الهندسة.
سنستخدم إستراتيجية حل المشكلات الخاصة بتطبيقات الهندسة، مع تعديلات طفيفة، لإعطائنا خطة لحل التطبيقات باستخدام الصيغ من أي تخصص.
- اقرأ المشكلة وتأكد من فهم جميع الكلمات والأفكار. عند الاقتضاء، ارسم شكلًا وقم بتسميته بالمعلومات المحددة.
- حدد ما نبحث عنه.
- قم بتسمية ما نبحث عنه عن طريق اختيار متغير لتمثيله.
- ترجم إلى معادلة بكتابة الصيغة أو النموذج المناسب للموقف. استبدل المعلومات المعطاة.
- حل المعادلة باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
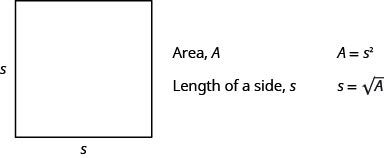
استخدمنا الصيغة A=L·W لإيجاد مساحة المستطيل بطول L وعرض W. المربع هو مستطيل يتساوى فيه الطول والعرض. إذا سمحنا لنا أن نكون طول ضلع المربع، فإن مساحة المربع هي\(s^2\).
\(A=s^2\)تُعطينا الصيغة مساحة المربع إذا عرفنا طول الضلع. ماذا لو أردنا إيجاد طول ضلع لمنطقة معينة؟ ثم نحتاج إلى حل المعادلة لـ s.
\[\begin{array}{ll} {}&{A=s^2}\\ {\text{Take the square root of both sides.}}&{\sqrt{A}=\sqrt{s^2}}\\ {\text{Simplify.}}&{s=\sqrt{A}}\\ \nonumber \end{array}\]
يمكننا استخدام الصيغة\(s=\sqrt{A}\) لإيجاد طول ضلع مربع لمساحة معينة.
سنعرض مثالاً على ذلك في المثال التالي.
يريد مايك وليشيل إنشاء فناء مربع. لديهم ما يكفي من الخرسانة لتمهيد مساحة 200 قدم مربع. استخدم الصيغة\(s=\sqrt{A}\) للعثور على طول كل جانب من الفناء. قرِّب إجابتك لأقرب عُشر قدم.
- إجابة
-
الخطوة 1. اقرأ المشكلة. ارسم شكلًا وقم
بتسميته بالمعلومات المعطاة.
A = 200 قدم مربع الخطوة 2. حدد ما تبحث عنه. طول جانب الفناء المربع. الخطوة 3. قم بتسمية ما تبحث عنه عن طريق
اختيار متغير لتمثيله.دعونا = طول الضلع. الخطوة 4. ترجم إلى معادلة بكتابة الصيغة أو النموذج
المناسب للموقف.
استبدل المعلومات المعطاة.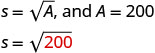
الخطوة 5. حل المعادلة باستخدام
تقنيات الجبر الجيدة. قرِّب إلى منزلة عشرية واحدة.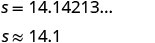
الخطوة 6. تحقق من الإجابة في المشكلة
وتأكد من أنها منطقية.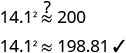
هذا قريب بما يكفي لأننا قمنا بتقريب الجذر
التربيعي.
هل الفناء ذو الجانب 14.1 قدمًا معقول؟
نعم.الخطوة 7. أجب على السؤال
بجملة كاملة.يجب أن يكون كل جانب من جوانب الفناء 14.1 قدمًا.
تريد كاتي زرع حديقة مربعة في فناء منزلها الأمامي. لديها ما يكفي من الاحمق لتغطية مساحة 370 قدمًا مربعًا. استخدم الصيغة\(s=\sqrt{A}\) للعثور على طول كل جانب من حديقتها. قرِّب إجابتك لأقرب عُشر قدم.
- إجابة
-
19.2 قدم
يريد سيرجيو صنع فسيفساء مربعة كترصيع لطاولة يقوم ببنائها. لديه ما يكفي من البلاط لتغطية مساحة 2704 سم مربع. استخدم الصيغة\(s=\sqrt{A}\) لإيجاد طول كل جانب من الفسيفساء الخاصة به. قرِّب إجابتك لأقرب عُشر قدم.
- إجابة
-
52.0 سم
تطبيق آخر للجذور المربعة يتعلق بالجاذبية.
على الأرض، إذا سقط جسم من ارتفاع قدم، يتم العثور على الوقت بالثواني الذي سيستغرقه الوصول إلى الأرض باستخدام الصيغة،
\(t=\frac{\sqrt{h}}{4}\)
على سبيل المثال، إذا سقط جسم من ارتفاع 64 قدمًا، يمكننا إيجاد الوقت المستغرق للوصول إلى الأرض عن طريق استبدال h=64 في الصيغة.
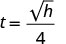 |
|
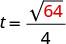 |
|
| خذ الجذر التربيعي لـ 64. | 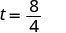 |
| قم بتبسيط الكسر. | 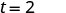 |
قد يستغرق الأمر ثانيتين حتى يصل جسم تم إسقاطه من ارتفاع 64 قدمًا إلى الأرض.
أسقطت كريستي نظارتها الشمسية من جسر على ارتفاع 400 قدم فوق النهر. استخدم الصيغة\(t=\frac{\sqrt{h}}{4}\) للعثور على عدد الثواني التي استغرقتها النظارات الشمسية للوصول إلى النهر.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما تبحث عنه. الوقت الذي تستغرقه النظارات الشمسية للوصول إلى
النهر.الخطوة 3. قم بتسمية ما تبحث عنه عن طريق
اختيار متغير لتمثيله.دعها = الوقت. الخطوة 4. ترجم إلى معادلة بكتابة الصيغة أو النموذج
المناسب للموقف.
استبدل المعلومات المقدمة.

الخطوة 5. حل المعادلة باستخدام
تقنيات الجبر الجيدة.

الخطوة 6. تحقق من الإجابة في المشكلة
وتأكد من أنها منطقية.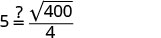

5=5 ✓هل تبدو 5 ثوان معقولة؟
نعم.الخطوة 7. أجب على السؤال
بجملة كاملة.سوف يستغرق الأمر 5 ثوانٍ حتى تصل النظارات الشمسية
إلى الماء.
أسقطت طائرة هليكوبتر حزمة إنقاذ من ارتفاع 1296 قدمًا. استخدم الصيغة\(t=\frac{\sqrt{h}}{4}\) للعثور على عدد الثواني التي استغرقتها الحزمة للوصول إلى الأرض.
- إجابة
-
9 ثوانٍ
قامت غسالة النوافذ بإسقاط ممسحة مطاطية من منصة على ارتفاع 196 قدمًا فوق الرصيف. استخدم الصيغة\(t=\frac{\sqrt{h}}{4}\) للعثور على عدد الثواني التي استغرقتها الممسحة للوصول إلى الرصيف.
- إجابة
-
3.5 ثانية
يقوم ضباط الشرطة الذين يحققون في حوادث السيارات بقياس طول علامات الانزلاق على الرصيف. ثم يستخدمون الجذور التربيعية لتحديد السرعة، بالأميال في الساعة، التي كانت تسير بها السيارة قبل الضغط على المكابح.
إذا كان طول علامات الانزلاق هو d قدمًا، فيمكن العثور على سرعة السيارة أو الثواني قبل استخدام الفرامل باستخدام الصيغة،
\(s=\sqrt{24d}\)
بعد حادث سيارة، بلغ قياس علامات الانزلاق لسيارة واحدة 190 قدمًا. استخدم الصيغة\(s=\sqrt{24d}\) للعثور على سرعة السيارة قبل استخدام الفرامل. قرِّب إجابتك لأقرب جزء من عشرة.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما نبحث عنه. سرعة السيارة. الخطوة 3. اذكر ما نبحث عنه. دعونا = السرعة. الخطوة 4. ترجم إلى معادلة بكتابة الصيغة المناسبة. 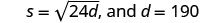
استبدل المعلومات المعطاة. 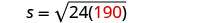
الخطوة 5. حل المعادلة. 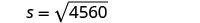
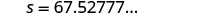
قرِّب إلى منزلة عشرية واحدة. 
الخطوة 6. تحقق من الإجابة في المشكلة.
67.5≈؟ 24 (190) √
67.5≈؟ 4560√
67.5≈؟ 67.5277...هل سرعة 67.5 ميل في الساعة معقولة؟ نعم. الخطوة 7. أجب على السؤال بجملة كاملة. كانت سرعة السيارة حوالي 67.5 ميل في الساعة.
قام محقق الحوادث بقياس علامات انزلاق السيارة. كان طول علامات الانزلاق 76 قدمًا. استخدم الصيغة\(s=\sqrt{24d}\) للعثور على سرعة السيارة قبل استخدام الفرامل. قرِّب إجابتك لأقرب جزء من عشرة.
- إجابة
-
42.7 قدم
كانت علامات انزلاق السيارة المتورطة في حادث بطول 122 قدمًا. استخدم الصيغة\(s=\sqrt{24d}\) للعثور على سرعة السيارة قبل استخدام الفرامل. قرِّب إجابتك لأقرب جزء من عشرة.
- إجابة
-
54.1 قدم
المفاهيم الرئيسية
- لحل معادلة جذرية:
- اعزل الجذر على أحد طرفي المعادلة.
- قم بمربع طرفي المعادلة.
- حل المعادلة الجديدة.
- تحقق من الإجابة. قد لا تعمل بعض الحلول التي تم الحصول عليها في المعادلة الأصلية.
- حل التطبيقات باستخدام الصيغ
- اقرأ المشكلة وتأكد من فهم جميع الكلمات والأفكار. عند الاقتضاء، ارسم شكلًا وقم بتسميته بالمعلومات المحددة.
- حدد ما نبحث عنه.
- قم بتسمية ما نبحث عنه عن طريق اختيار متغير لتمثيله.
- ترجم إلى معادلة بكتابة الصيغة أو النموذج المناسب للموقف. استبدل المعلومات المعطاة.
- حل المعادلة باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
- مساحة المربع
- الأجسام الساقطة
- على الأرض، إذا سقط جسم من ارتفاع hf foot، يتم العثور على الوقت بالثواني الذي سيستغرقه الوصول إلى الأرض باستخدام الصيغة\(t=\frac{\sqrt{h}}{4}\).
- علامات الانزلاق وسرعة السيارة
- إذا كان طول علامات الانزلاق هو d قدمًا، فيمكن العثور على سرعة السيارة أو الثواني قبل استخدام الفرامل باستخدام الصيغة\(s=\sqrt{24d}\).
مسرد المصطلحات
- معادلة جذرية
- المعادلة التي يكون فيها المتغير في جذر الجذر التربيعي تسمى المعادلة الجذرية.


