9.5: تقسيم الجذور المربعة
- Page ID
- 200111
في نهاية هذا القسم، ستكون قادرًا على:
- قسّم الجذور المربعة
- ترشيد القاسم أحادي المدة
- ترشيد القاسم ثنائي المدة
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- أوجد الكسر\(\frac{5}{8}\) المكافئ للقاسم ٤٨.
إذا فاتتك هذه المشكلة، راجع التمرين 1.6.1. - قم بالتبسيط:\((\sqrt{5})^2\).
إذا فاتتك هذه المشكلة، راجع المثال 9.4.13. - اضرب: (7+3x) (7−3x).
إذا فاتتك هذه المشكلة، راجع التمرين 6.4.22.
تقسيم الجذور المربعة
نحن نعلم أننا نبسط الكسور عن طريق إزالة العوامل المشتركة بين البسط والمقام. عندما يكون لدينا كسر بجذر تربيعي في البسط، نقوم أولاً بتبسيط الجذر التربيعي. ثم يمكننا البحث عن العوامل المشتركة.
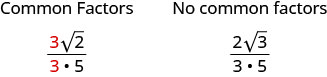
قم بالتبسيط:\(\frac{\sqrt{54}}{6}\)
- إجابة
-
\(\frac{\sqrt{54}}{6}\) تبسيط الراديكالية. \(\frac{\sqrt{9}·\sqrt{6}}{6}\) قم بالتبسيط. \(\frac{3\sqrt{6}}{6}\) قم بإزالة العوامل المشتركة. \(\frac{3\sqrt{6}}{3·2}\) قم بالتبسيط. \(\frac{\sqrt{6}}{2}\)
قم بالتبسيط:\(\frac{\sqrt{32}}{8}\).
- إجابة
-
\(\frac{\sqrt{2}}{2}\)
قم بالتبسيط:\(\frac{\sqrt{75}}{15}\).
- إجابة
-
\(\frac{\sqrt{3}}{3}\)
قم بالتبسيط:\(\frac{6−\sqrt{24}}{12}\).
- إجابة
-
\(\frac{6−\sqrt{24}}{12}\) تبسيط الراديكالية. \(\frac{6−\sqrt{4}·\sqrt{6}}{12}\) قم بالتبسيط. \(\frac{6−2\sqrt{6}}{12}\) ضع في اعتبارك العامل المشترك من البسط. \(\frac{2(3−\sqrt{6})}{12}\) قم بإزالة العوامل المشتركة. \(\frac{2(3−\sqrt{6})}{2·6}\) قم بالتبسيط. \(\frac{3−\sqrt{6}}{6}\)
قم بالتبسيط:\(\frac{8−\sqrt{40}}{10}\).
- إجابة
-
\(\frac{4−\sqrt{10}}{5}\)
قم بالتبسيط:\(\frac{10−\sqrt{75}}{20}\).
- إجابة
-
\(\frac{5−\sqrt{3}}{4}\)
لقد استخدمنا خاصية حاصل القسمة للجذور التربيعية لتبسيط الجذور التربيعية للكسور. تقول خاصية حاصل القسمة للجذور المربعة
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)،\(b \ne 0\).
في بعض الأحيان سنحتاج إلى استخدام خاصية حاصل القسمة للجذور المربعة «في الاتجاه المعاكس» لتبسيط الكسر ذي الجذور التربيعية.
\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)،\(b \ne 0\).
سنعيد كتابة خاصية حاصل القسمة للجذور المربعة حتى نرى كلا الاتجاهين معًا. تذكر: نفترض أن جميع المتغيرات أكبر من أو تساوي الصفر بحيث تكون جذورها التربيعية أعدادًا حقيقية.
إذا كانت a و b أرقامًا حقيقية غير سالبة ثم\(b \ne 0\)
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)و\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
سنستخدم خاصية حاصل القسمة للجذور التربيعية «في الاتجاه المعاكس» عندما يكون الكسر الذي نبدأ به هو حاصل قسمة جذرين تربيعيين، ولا يمثل الجذر مربعًا مثاليًا. عندما نكتب الكسر في جذر تربيعي واحد، قد نجد عوامل مشتركة في البسط والمقام.
قم بالتبسيط:\(\frac{\sqrt{27}}{\sqrt{75}}\)
- إجابة
-
\(\frac{\sqrt{27}}{\sqrt{75}}\) لا يُعد أي من radicand مربعًا مثاليًا، لذا أعد الكتابة باستخدام خاصية حاصل القسمة للجذر التربيعي. \(\sqrt{\frac{27}{75}}\) أزل العوامل المشتركة في البسط والمقام. \(\sqrt{\frac{9}{25}}\) قم بالتبسيط. \(\frac{3}{5}\)
قم بالتبسيط:\(\frac{\sqrt{48}}{\sqrt{108}}\)
- إجابة
-
\(\frac{2}{3}\)
قم بالتبسيط:\(\frac{\sqrt{96}}{\sqrt{54}}\)
- إجابة
-
\(\frac{4}{3}\)
سنستخدم خاصية حاصل القسمة للأسس\(\frac{a^m}{a^n}=a^{m−n}\)، عندما تكون لدينا متغيرات ذات أسس في الجذور.
قم بالتبسيط:\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)
- إجابة
-
\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\) لا يُعد أي من radicand مربعًا مثاليًا، لذا أعد الكتابة باستخدام خاصية حاصل القسمة للجذر التربيعي. \(\sqrt{\frac{6y^5}{2y}}\) أزل العوامل المشتركة في البسط والمقام. \(\sqrt{3y^4}\) قم بالتبسيط. \(y^2\sqrt{3}\)
قم بالتبسيط:\(\frac{\sqrt{12r^3}}{\sqrt{6r}}\).
- إجابة
-
\(r\sqrt{2}\)
قم بالتبسيط:\(\frac{\sqrt{14p^9}}{\sqrt{2p^5}}\)
- إجابة
-
\(p^2\sqrt{7}\)
قم بالتبسيط:\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)
- إجابة
-
\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\) أعد الكتابة باستخدام خاصية حاصل القسمة للجذور التربيعية. \(\sqrt{\frac{72x^3}{162x}}\) قم بإزالة العوامل المشتركة. \(\sqrt{\frac{18·4·x^2·x}{18·9·x}}\) قم بالتبسيط. \(\sqrt{\frac{4x^2}{9}}\) تبسيط الراديكالية. \(\frac{2x}{3}\)
قم بالتبسيط:\(\frac{\sqrt{50s^3}}{\sqrt{128s}}\).
- إجابة
-
\(\frac{5s}{8}\)
قم بالتبسيط:\(\frac{\sqrt{75q^5}}{\sqrt{108q}}\).
- إجابة
-
\(\frac{5q^2}{6}\)
قم بالتبسيط:\(\frac{\sqrt{147ab^8}}{\sqrt{3a^3b^4}}\).
- إجابة
-
\(\frac{\sqrt{147ab^8}}{\sqrt{3a^{3}b^{4}}}\) أعد الكتابة باستخدام خاصية حاصل القسمة للجذور التربيعية. \(\sqrt{\frac{147ab^8}{3a^{3}b^{4}}}\) قم بإزالة العوامل المشتركة. \ (\ sqrt {\ frac {49b^4} {a^2}}\ تبسيط الراديكالية. \(\frac{7b^2}{a}\)
قم بالتبسيط:\(\frac{\sqrt{162x^{10}y^{2}}}{\sqrt{2x^6y^6}}\).
- إجابة
-
\(\frac{9x^2}{y^2}\)
قم بالتبسيط:\(\frac{\sqrt{300m^{3}n^{7}}}{\sqrt{3m^{5}n}}\).
- إجابة
-
\(\frac{10n^3}{m}\)
ترشيد قاسم مصطلح واحد
قبل أن تصبح الآلة الحاسبة أداة للحياة اليومية، تم استخدام جداول الجذور التربيعية للعثور على القيم التقريبية للجذور التربيعية. يوضِّح الشكل جزءًا من جدول المربعات والجذور التربيعية. يتم تقريب الجذور التربيعية بخمس منازل عشرية في هذا الجدول.
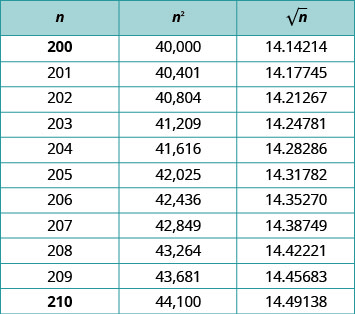
إذا احتاج شخص ما إلى تقريب كسر يحتوي على جذر تربيعي في المقام، فهذا يعني إجراء قسمة طويلة باستخدام مقسوم المركز العشري الخماسي. كانت هذه عملية مرهقة للغاية.
لهذا السبب، تم تطوير عملية تسمى ترشيد المقام. يتم تحويل الكسر الذي يحتوي على جذر في المقام إلى كسر مكافئ مقامه عدد صحيح. لا تزال هذه العملية مستخدمة اليوم وهي مفيدة في مجالات الرياضيات الأخرى أيضًا.
إن عملية تحويل كسر ذي جذر في المقام إلى كسر مكافئ مقامه عدد صحيح تسمى ترشيد المقام.
الجذور التربيعية للأرقام التي ليست مربعات مثالية هي أرقام غير منطقية. عندما نقوم بترشيد المقام، نكتب كسرًا مكافئًا برقم نسبي في المقام.
لنلقِ نظرة على مثال رقمي.
\[\begin{array}{ll} {\text{Suppose we need an approximate value for the fraction.}}&{\frac{1}{\sqrt{2}}}\\ {\text{A five decimal place approximation to} \sqrt{2} \text{is} 1.41421}&{\frac{1}{1.41421}}\\ {\text{Without a calculator, would you want to do this division?}}&{1.41421) \overline{1.0}}\\ \nonumber \end{array}\]
ولكن يمكننا إيجاد كسر مكافئ\(\frac{1}{\sqrt{2}}\) بضرب البسط والمقام في\(\sqrt{2}\).
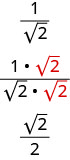
الآن إذا كنا بحاجة إلى قيمة تقريبية، فإننا نقسم\(2) \overline{1.41421}\). هذا أسهل بكثير.
على الرغم من توفر الآلات الحاسبة في كل مكان تقريبًا، إلا أنه لا يزال يتعين ترشيد الكسر الذي يحتوي على جذر في المقام. لا يعتبر الأمر مبسطًا إذا كان المقام يحتوي على جذر تربيعي.
وبالمثل، لا يعتبر الجذر التربيعي مبسطًا إذا كان الجذر يحتوي على كسر.
يعتبر الجذر التربيعي مبسطًا إذا كان هناك
- لا توجد عوامل مربعة مثالية في الراديكاند
- لا توجد كسور في الراديكاند
- لا توجد جذور مربعة في مقام الكسر
لترشيد القاسم، نستخدم الخاصية التي\((\sqrt{a})^2=a\). If we square an irrational square root, we get a rational number.
سنستخدم هذه الخاصية لترشيد المقام في المثال التالي.
قم بالتبسيط:\(\frac{4}{\sqrt{3}}\).
- إجابة
-
لإزالة الجذر التربيعي من المقام، نضربه بنفسه. للحفاظ على تساوي الكسور، نضرب كلا من البسط والمقام في نفس العامل.
\(\frac{4}{\sqrt{3}}\)
اضرب كل من البسط والمقام في\(\sqrt{3}\)\(\frac{4·\sqrt{3}}{\sqrt{3}·\sqrt{3}}\) قم بالتبسيط. \(\frac{4\sqrt{3}}{3}\)
قم بالتبسيط:\(\frac{5}{\sqrt{3}}\).
- إجابة
-
\(\frac{5\sqrt{3}}{3}\)
قم بالتبسيط:\(\frac{6}{\sqrt{5}}\).
- إجابة
-
\(\frac{6\sqrt{5}}{5}\)
قم بالتبسيط:\(−\frac{8}{3\sqrt{6}}\)
- إجابة
-
لإزالة الجذر التربيعي من المقام، نضربه بنفسه. للحفاظ على تساوي الكسور، نضرب كلا من البسط والمقام في\(\sqrt{6}\).
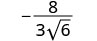
اضرب كل من البسط والمقام في\(\sqrt{6}\). 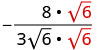
قم بالتبسيط. 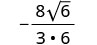
قم بإزالة العوامل المشتركة. 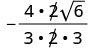
قم بالتبسيط. 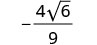
قم بالتبسيط:\(\frac{5}{2\sqrt{5}}\).
- إجابة
-
\(\frac{\sqrt{5}}{2}\)
قم بالتبسيط:\(−\frac{9}{4\sqrt{3}}\).
- إجابة
-
\(−\frac{3\sqrt{3}}{4}\)
قم دائمًا بتبسيط الراديكالية في المقام أولاً، قبل تبريرها. بهذه الطريقة تظل الأرقام أصغر ويسهل التعامل معها.
قم بالتبسيط:\(\sqrt{\frac{5}{12}}\).
- إجابة
-
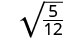
الكسر ليس مربعًا مثاليًا، لذا أعد الكتابة باستخدام خاصية
Quotient.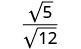
قم بتبسيط المقام. 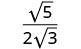
ترشيد المقام. 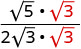
قم بالتبسيط. 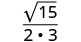
قم بالتبسيط. 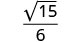
قم بالتبسيط:\(\sqrt{\frac{7}{18}}\).
- إجابة
-
\(\frac{\sqrt{14}}{6}\)
قم بالتبسيط:\(\sqrt{\frac{3}{32}}\).
- إجابة
-
\(\frac{\sqrt{6}}{8}\)
قم بالتبسيط:\(\sqrt{\frac{11}{28}}\)
- إجابة
-
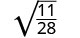
أعد الكتابة باستخدام خاصية حاصل القسمة. 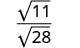
قم بتبسيط المقام. 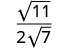
ترشيد المقام. 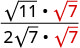
قم بالتبسيط. 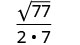
قم بالتبسيط. 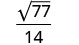
قم بالتبسيط:\(\sqrt{\frac{3}{27}}\).
- إجابة
-
\(\frac{1}{3}\)
قم بالتبسيط:\(\sqrt{\frac{10}{50}}\)
- إجابة
-
\(\frac{\sqrt{5}}{5}\)
ترشيد المقام ثنائي المدة
عندما يكون مقام الكسر عبارة عن مجموع أو فرق ذي جذور مربعة، فإننا نستخدم نمط حاصل ضرب الكسور لترشيد المقام.
\[\begin{array}{ll} {(a−b)(a+b)}&{(2−\sqrt{5})(2+\sqrt{5})}\\ {a^2−b^2}&{2^2−(\sqrt{5})^2}\\ {}&{4−5}\\ {}&{−1}\\ \nonumber \end{array}\]
عندما نضرب معادلة ذات حدين تتضمن جذرًا تربيعيًا في مترافقه، فإن المنتج ليس له جذور مربعة.
قم بالتبسيط:\(\frac{4}{4+\sqrt{2}}\).
- إجابة
-
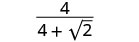
اضرب البسط والمقام في مترافق المقام. 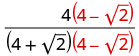
اضرب المترافقات في المقام. 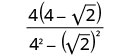
قم بتبسيط المقام. 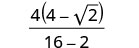
قم بتبسيط المقام. 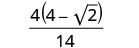
أزل العوامل المشتركة من البسط والمقام. 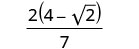
نترك البسط في شكل معمول لتسهيل البحث عن العوامل المشتركة بعد تبسيط المقام.
قم بالتبسيط:\(\frac{2}{2+\sqrt{3}}\).
- إجابة
-
\(\frac{2(2−\sqrt{3})}{1}\)
قم بالتبسيط:\(\frac{5}{5+\sqrt{3}}\).
- إجابة
-
\(\frac{5(5−\sqrt{3})}{22}\)
قم بالتبسيط:\(\frac{5}{2−\sqrt{3}}\).
- إجابة
-
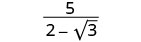
اضرب البسط والمقام في مترافق المقام. 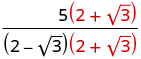
اضرب المترافقات في المقام. 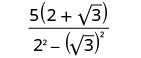
قم بتبسيط المقام. 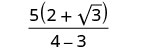
قم بتبسيط المقام. 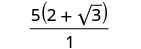
قم بالتبسيط. 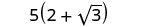
قم بالتبسيط:\(\frac{3}{1−\sqrt{5}}\).
- إجابة
-
\(−\frac{3(1+\sqrt{5})}{4}\)
قم بالتبسيط:\(\frac{2}{4−\sqrt{6}}\).
- إجابة
-
\(\frac{4+\sqrt{6}}{5}\)
قم بالتبسيط:\(\frac{\sqrt{3}}{\sqrt{u}−\sqrt{6}}\).
- إجابة
-
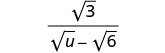
اضرب البسط والمقام في مترافق المقام. 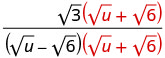
اضرب المترافقات في المقام. 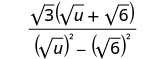
قم بتبسيط المقام. 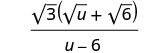
قم بالتبسيط:\(\frac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- إجابة
-
\(\frac{\sqrt{5}(\sqrt{x}−\sqrt{2})}{x−2}\)
قم بالتبسيط:\(\frac{\sqrt{10}}{\sqrt{y}−\sqrt{3}}\).
- إجابة
-
\(\frac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y−3}\)
قم بالتبسيط:\(\frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}−\sqrt{7}}\).
- إجابة
-
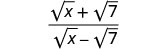
اضرب البسط والمقام في مترافق المقام. 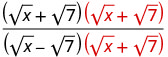
اضرب المترافقات في المقام. 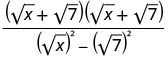
قم بتبسيط المقام. 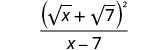
نحن لا نضع البسط في مربع. في الشكل المركب، يمكننا أن نرى أنه لا توجد عوامل مشتركة لإزالتها من البسط والمقام.
قم بالتبسيط:\(\frac{\sqrt{p}+\sqrt{2}}{\sqrt{p}−\sqrt{2}}\).
- إجابة
-
\(\frac{(\sqrt{p}+\sqrt{2})^2}{p−2}\)
قم بالتبسيط:\(\frac{\sqrt{q}−\sqrt{10}}{\sqrt{q}+\sqrt{10}}\).
- إجابة
-
\(\frac{(\sqrt{q}−\sqrt{10})^2}{q−10}\)
قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع التقسيم والترشيد.
- التقسيم والترشيد
المفاهيم الرئيسية
- خاصية حاصل القسمة للجذور التربيعية
- إذا كانت a و b أرقامًا حقيقية غير سالبة ثم\(b \ne 0\)
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)و\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
- إذا كانت a و b أرقامًا حقيقية غير سالبة ثم\(b \ne 0\)
- الجذور
التربيعية المبسطة يعتبر الجذر التربيعي مبسطًا إذا كان موجودًا- لا توجد عوامل مربعة مثالية في الراديكوند
- لا توجد كسور في الراديكاند
- لا توجد جذور مربعة في مقام الكسر
مسرد المصطلحات
- ترشيد المقام
- إن عملية تحويل كسر ذي جذر في المقام إلى كسر مكافئ مقامه عدد صحيح تسمى ترشيد المقام.


