9.1: تبسيط واستخدام الجذور التربيعية
- Page ID
- 200169
في نهاية هذا القسم، ستكون قادرًا على:
- تبسيط التعبيرات باستخدام الجذور التربيعية
- تقدير الجذور التربيعية
- جذور مربعة تقريبية
- قم بتبسيط التعبيرات المتغيرة بجذور مربعة
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
تبسيط التعبيرات باستخدام الجذور التربيعية
تذكر أنه عندما يتم ضرب الرقم n في حد ذاته، فإننا نكتبه\(n^2\) ونقرأه «n squared». على سبيل المثال،\(15^2\) يُقرأ كـ «15 مربعًا»، ويُسمى 225 مربع 15، منذ ذلك الحين\(15^2=225\).
إذا كان\(n^2=m\) m هو مربع n.
في بعض الأحيان سنحتاج إلى النظر إلى العلاقة بين الأرقام ومربعاتها في الاتجاه المعاكس. ولأن 225 هو مربع 15، يمكننا أيضًا القول أن 15 هو الجذر التربيعي لـ 225. يُطلق على الرقم الذي مربعه m اسم الجذر التربيعي لـ m.
إذا كان\(n^2=m\) n هو الجذر التربيعي لـ m.
ملاحظة\((−15)^2=225\) also, so −15 is also a square root of 225. Therefore, both 15 and −15 are square roots of 225.
لذلك، كل عدد موجب له جذران مربعان - أحدهما موجب والآخر سالب. ماذا لو أردنا فقط الجذر التربيعي الموجب لعدد موجب؟ تشير العلامة الراديكالية إلى الجذر التربيعي الإيجابي.\(\sqrt{m}\) يُطلق على الجذر التربيعي الموجب أيضًا الجذر التربيعي الرئيسي.
نستخدم أيضًا العلامة الجذرية للجذر التربيعي للصفر. لأن\(0^2=0\)،\(\sqrt{0}=0\). لاحظ أن الصفر يحتوي على جذر مربع واحد فقط.
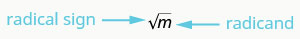
\(\sqrt{m}\)يُقرأ على أنه «الجذر التربيعي لـ m».
إذا\(m=n^2\)، إذن\(\sqrt{m}=n\)، من أجل\(n \ge 0\).
الجذر التربيعي لـ m،\(\sqrt{m}\)، هو الرقم الموجب الذي مربعه هو m.
نظرًا لأن 15 هو الجذر التربيعي الموجب لـ 225، فإننا نكتب\(\sqrt{225}=15\). Fill in الشكل لإنشاء جدول للجذور التربيعية يمكنك الرجوع إليه أثناء عملك في هذا الفصل.

نحن نعلم أن كل رقم موجب له جذران تربيعيان وأن العلامة الجذرية تشير إلى الموجب. نحن نكتب\(\sqrt{225}=15\). إذا أردنا إيجاد الجذر التربيعي السالب لعدد ما، فإننا نضع القيمة السالبة أمام العلامة الجذرية. على سبيل المثال،\(−\sqrt{225}=−15\).
قم بالتبسيط:
- \(\sqrt{36}\)
- \(\sqrt{196}\)
- \(−\sqrt{81}\)
- \(−\sqrt{289}\).
- إجابة
-
1.
\[\begin{array}{ll} {}&{\sqrt{36}}\\ {\text{Since} 6^2=36}&{6}\\ \end{array}\]
2.
\[\begin{array}{ll} {}&{\sqrt{196}}\\ {\text{Since} 14^2=196}&{14}\\ \end{array}\]
3.
\[\begin{array}{ll} {}&{−\sqrt{81}}\\ {\text{The negative is in front of the radical sign}}&{−9}\\ \end{array}\]
4.
\[\begin{array}{ll} {}&{−\sqrt{289}}\\ {\text{The negative is in front of the radical sign}}&{−17}\\ \end{array}\]
قم بالتبسيط:
- \(−\sqrt{49}\)
- \(\sqrt{225}\).
- إجابة
-
- −7
- 15
تبسيط:
- \(\sqrt{64}\)
- \(−\sqrt{121}\).
- إجابة
-
- 8
- −11
قم بالتبسيط:
- \(\sqrt{−169}\)
- \( −\sqrt{64}\)
- إجابة
-
1.
\[\begin{array}{ll} {}&{\sqrt{−169}}\\ {\text{There is no real number whose square is} s−169}&{\sqrt{−169} \text{is not a real number.}}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{−\sqrt{64}}\\ {\text{The negative is in front of the radical sign}}&{−8}\\ \end{array}\]
قم بالتبسيط:
- \(\sqrt{−196}\)
- \(−\sqrt{81}\).
- إجابة
-
- ليس رقمًا حقيقيًا
- −9
قم بالتبسيط:
- \(−\sqrt{49}\)
- \(\sqrt{ −121}\).
- إجابة
-
- −7
- ليس رقمًا حقيقيًا
عند استخدام ترتيب العمليات لتبسيط تعبير له جذور مربعة، فإننا نتعامل مع الراديكالية كرمز تجميع.
قم بالتبسيط:
- \(\sqrt{25} +\sqrt{144}\)
- \(\sqrt{25+144}\).
- إجابة
-
1.
\[\begin{array}{ll} {}&{\sqrt{25} +\sqrt{144}}\\ {\text{Use the order of operations}}&{5+12}\\ {\text{Simplify.}}&{17}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{25+144}}\\ {\text{Simplify under the radical sign.}}&{\sqrt{169}}\\ {\text{Simplify.}}&{13}\\ \end{array}\]
لاحظ الإجابات المختلفة في الأجزاء 1 و 2!
قم بالتبسيط:
- \(\sqrt{9}+\sqrt{16}\)
- \(\sqrt{9+16}\).
- إجابة
-
- 7
- 5
قم بالتبسيط:
- \(\sqrt{64+225}\)
- \(\sqrt{64}+\sqrt{225}\).
- إجابة
-
- 17
- 23
تقدير الجذور التربيعية
حتى الآن نظرنا فقط في الجذور التربيعية للأرقام المربعة المثالية. الجذور التربيعية للأرقام الأخرى ليست أرقامًا صحيحة. انظر إلى الجدول أدناه.
| رقم | الجذر التربيعي |
|---|---|
| 4 | \(\sqrt{4}=2\) |
| 5 | \(\sqrt{5}\) |
| 6 | \(\sqrt{6}\) |
| 7 | \(\sqrt{7}\) |
| 8 | \(\sqrt{8}\) |
| 9 | \(\sqrt{9}=3\) |
يجب أن تكون الجذور التربيعية للأرقام بين 4 و9 بين الرقمين الصحيحين المتتابعين 2 و3، وهي ليست أعدادًا صحيحة. استنادًا إلى النمط الموجود في الجدول أعلاه، يمكننا القول أنه\(\sqrt{5}\) يجب أن يكون بين 2 و 3. باستخدام رموز عدم المساواة، نكتب:
\(2<\sqrt{5}<3\)
قم بالتقدير\(\sqrt{60}\) بين رقمين صحيحين متتاليين.
- إجابة
-
فكر في الأعداد المربعة المثالية الأقرب إلى 60. اصنع جدولًا صغيرًا من هذه المربعات المثالية وجذورها المربعة.
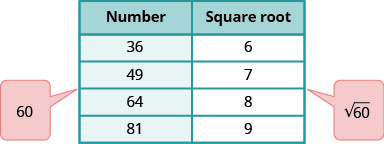
حدد موقع 60 بين مربعين مثاليين متتاليين. 
\(\sqrt{60}\)تقع بين جذورها المربعة. 
قدِّر الجذر التربيعي\(\sqrt{38}\) بين عددين صحيحين متتاليين.
- إجابة
-
\(6<\sqrt{38}<7\)
قدِّر الجذر التربيعي\(\sqrt{84}\) بين عددين صحيحين متتاليين.
- إجابة
-
\(9<\sqrt{84}<10\)
جذور مربعة تقريبية
هناك طرق رياضية لتقريب الجذور التربيعية، ولكن في الوقت الحاضر يستخدم معظم الناس الآلة الحاسبة للعثور عليها. ابحث عن\(\sqrt{x}\) المفتاح في الآلة الحاسبة الخاصة بك. ستستخدم هذا المفتاح لتقريب الجذور المربعة.
عندما تستخدم الآلة الحاسبة للعثور على الجذر التربيعي لرقم ليس مربعًا مثاليًا، فإن الإجابة التي تراها ليست الجذر التربيعي الدقيق. إنه تقدير تقريبي ودقيق لعدد الأرقام المعروضة على شاشة الآلة الحاسبة. رمز التقريب هو\(\approx\) ويتم قراءته «تقريبًا».
لنفترض أن الآلة الحاسبة تحتوي على شاشة مكونة من 10 أرقام. سوف ترى ذلك
\(\sqrt{5} \approx 2.236067978\)
إذا أردنا التقريب\(\sqrt{5}\) إلى منزلتين عشريتين، فسنقول
\(\sqrt{5} \approx 2.24\)
كيف نعرف أن هذه القيم تقريبية وليست القيم الدقيقة؟ انظر إلى ما يحدث عندما نربحها:
\[\begin{array}{c} {(2.236067978)^2=5.000000002}\\ {(2.24)^2=5.0176}\\ \end{array}\]
مربعاتها قريبة من 5، ولكنها لا تساوي بالضبط 5.
باستخدام مفتاح الجذر التربيعي في الآلة الحاسبة ثم التقريب إلى منزلتين عشريتين، يمكننا العثور على:
\[\begin{array}{c} {\sqrt{4}=2}\\ {\sqrt{5} \approx 2.24}\\ {\sqrt{6} \approx 2.45}\\ {\sqrt{7} \approx 2.65}\\ {\sqrt{8} \approx 2.83}\\ {\sqrt{9}=3}\\ \end{array}\]
قرِّب\(\sqrt{17}\) إلى منزلتين عشريتين.
- إجابة
-
\[\begin{array}{ll} {}&{\sqrt{17}}\\ {\text{Use the calculator square root key.}}&{4.123105626...}\\ {\text{Round to two decimal places.}}&{4.12}\\ {}&{\sqrt{17} \approx 4.12} \end{array}\]
قرِّب\(\sqrt{11}\) إلى منزلتين عشريتين.
- إجابة
-
\(\approx 3.32\)
قرِّب\(\sqrt{13}\) إلى منزلتين عشريتين.
- إجابة
-
\(\approx 3.61\)
تبسيط التعبيرات المتغيرة باستخدام الجذور التربيعية
ماذا لو كان علينا إيجاد جذر تربيعي للتعبير ذي المتغير؟ ضع في اعتبارك\(\sqrt{9x^2}\). هل يمكنك التفكير في تعبير يكون مربعه\(9x^2\)؟
\[\begin{array}{cc} {(?)^2=9x^2}&{}\\ {(3x)^2=9x^2}&{\text{so} \sqrt{9x^2}=3x}\\ \end{array}\]
عندما نستخدم العلامة الجذرية لأخذ الجذر التربيعي لتعبير متغير، يجب أن نحدد ذلك x≥0x≥0 للتأكد من حصولنا على الجذر التربيعي الرئيسي.
ومع ذلك، في هذا الفصل، سنفترض أن كل متغير في تعبير الجذر التربيعي يمثل عددًا غير سالب، وبالتالي لن نكتب\(x \ge 0\) بجوار كل جذر.
ماذا عن الجذور التربيعية للقوى العليا للمتغيرات؟ فكر في خاصية قوة الأسس التي استخدمناها في الفصل 6.
\((a^m)^n=a^{m·n}\)
إذا قمنا بالمربع\(a^m\)، فسيصبح الأس 2 متر.
\((a^m)^2=a^{2m}\)
كيف يساعدنا هذا في أخذ الجذور التربيعية؟ لنلقِ نظرة على بعضها:
\[\begin{array}{cc} {\sqrt{25u^8}=5u^4}&{\text{Because} (5u^4)^2=25u^8}\\ {\sqrt{16r^{20}}=4r^{10}}&{\text{Because} (4r^{10})^2=16r^{20}}\\ {\sqrt{196q^{36}}=14q^{18}}&{\text{Because} (14r^{18})^2=196q^{36}}\\ \end{array}\]
قم بالتبسيط:
- \(\sqrt{x^6}\)
- \(\sqrt{y^{16}}\)
- إجابة
-
1.
\[\begin{array}{ll} {}&{\sqrt{x^6}}\\ {\text{Since} (x^3)^2=x^6}&{x^3}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{y^{16}}}\\ {\text{Since} (y^8)^2=y^{16}}&{y^8}\\ \end{array}\]
قم بالتبسيط:
- \(\sqrt{y^8}\)
- \(\sqrt{z^{12}}\).
- إجابة
-
- \(y^4\)
- \(z^6\)
قم بالتبسيط:
- \(\sqrt{m^4}\)
- \(\sqrt{b^{10}}\).
- إجابة
-
- \(m^2\)
- \(b^5\)
قم بالتبسيط:\(\sqrt{16n^2}\)
- إجابة
-
\[\begin{array}{ll} {}&{\sqrt{16n^2}}\\ {\text{Since} (4n)^2=16n^2}&{4n}\\ \end{array}\]
قم بالتبسيط:\(\sqrt{64x^2}\).
- إجابة
-
\(8x\)
قم بالتبسيط:\(\sqrt{169y^2}\).
- إجابة
-
\(13y\)
قم بالتبسيط:\(−\sqrt{81c^2}\).
- إجابة
-
\[\begin{array}{ll} {}&{−\sqrt{81c^2}}\\ {\text{Since} (9c)^2=81c^2}&{−9c}\\ \end{array}\]
قم بالتبسيط:\(−\sqrt{121y^2}\).
- إجابة
-
\(−11y\)
قم بالتبسيط:\(−\sqrt{100p^2}\).
- إجابة
-
\(−10p\)
قم بالتبسيط:\(\sqrt{36x^{2}y^{2}}\).
- إجابة
-
\[\begin{array}{ll} {}&{\sqrt{36x^{2}y^{2}}}\\ {\text{Since} (6xy)^2=\sqrt{36x^{2}y^{2}}}&{6xy}\\ \end{array}\]
قم بالتبسيط:\(\sqrt{100a^{2}b^{2}}\).
- إجابة
-
10ab
قم بالتبسيط:\(\sqrt{225m^{2}n^{2}}\).
- إجابة
-
15 دقيقة
قم بالتبسيط:\(\sqrt{64p^{64}}\).
- إجابة
-
\[\begin{array}{ll} {}&{\sqrt{64p^{64}}}\\ {\text{Since} (8p^8)^2=\sqrt{64p^{64}}}&{8p^8}\\ \end{array}\]
قم بالتبسيط:\(\sqrt{49x^{30}}\).
- إجابة
-
\(7x^{15}\)
قم بالتبسيط:\(\sqrt{81w^{36}}\)
- إجابة
-
\(9w^{18}\)
قم بالتبسيط:\(\sqrt{121a^{6}b^{8}}\)
- إجابة
-
\[\begin{array}{ll} {}&{\sqrt{121a^{6}b^{8}}}\\ {\text{Since} (11a^{3}b^{4})^2=\sqrt{121a^{6}b^{8}}}&{11a^{3}b^{4}}\\ \end{array}\]
قم بالتبسيط:\(\sqrt{169x^{10}y^{14}}\)
- إجابة
-
\(13x^{5}y^{7}\)
قم بالتبسيط:\(\sqrt{144p^{12}q^{20}}\)
- إجابة
-
\(\sqrt{12p^{6}q^{10}}\)
قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام الجذور التربيعية.
- جذور مربعة
المفاهيم الرئيسية
- لاحظ أن الجذر التربيعي للرقم السالب ليس رقمًا حقيقيًا.
- كل عدد موجب له جذران تربيعيان، أحدهما إيجابي والآخر سالب. الجذر التربيعي الموجب لعدد موجب هو الجذر التربيعي الأساسي.
- يمكننا تقدير الجذور التربيعية باستخدام المربعات المثالية القريبة.
- يمكننا تقريب الجذور التربيعية باستخدام الآلة الحاسبة.
- عندما نستخدم العلامة الجذرية لأخذ الجذر التربيعي لتعبير متغير، يجب أن نحدد ذلك\(x \ge 0\) للتأكد من حصولنا على الجذر التربيعي الرئيسي.
مسرد المصطلحات
- مربع الرقم
-
- إذا كان\(n^2=m\) m هو مربع n
- الجذر التربيعي لعدد
-
- إذا كان\(n^2=m\) n هو الجذر التربيعي لـ m
- تدوين الجذر التربيعي
-
- إذا\(m=n^2\)، إذن\(\sqrt{m}=n\). نقرأ\(\sqrt{m}\) باسم «الجذر التربيعي لـ m».


