الفصل 8 تمارين المراجعة
- Page ID
- 200338
تمارين مراجعة الفصل
تبسيط التعبيرات الكسرية
حدد القيم التي لا يتم تعريف التعبير العقلاني لها
في التمارين التالية، حدد القيم التي لم يتم تعريف التعبير العقلاني لها.
\(\dfrac{2a+1}{3a−2}\)
- إجابة
-
\(a \ne \dfrac{2}{3}\)
\(\dfrac{b−3}{b^2−16}\)
\(\dfrac{3xy^2}{5y}\)
- إجابة
-
\(y \ne 0\)
\(\dfrac{u−3}{u^2−u−30}\)
إيجاد قيمة التعبيرات الكسرية
في التمارين التالية، قم بتقييم التعبيرات النسبية للقيم المُعطاة.
\(\dfrac{4p−1}{p^2+5}\)عندما\(p=−1\)
- إجابة
-
\(−\dfrac{5}{6}\)
\(\dfrac{q^2−5}{q+3}\)عندما\(q=7\)
\(\dfrac{y^2−8}{y^2−y−2}\)عندما\(y=1\)
- إجابة
-
\(\dfrac{7}{2}\)
\(\dfrac{z^2+2}{4z−z^2}\)عندما\(z=3\)
في التمارين التالية، قم بالتبسيط.
\(\dfrac{10}{24}\)
- إجابة
-
\(\dfrac{5}{12}\)
\(\dfrac{8m^4}{16mn^3}\)
\(\dfrac{14a−14}{a−1}\)
- إجابة
-
\(14\)
\(\dfrac{b^2+7b+12}{b^2+8b+16}\)
تبسيط التعبيرات الكسرية باستخدام العوامل المعاكسة
في التمارين التالية، قم بالتبسيط.
\(\dfrac{c^2−c−2}{4−c^2}\)
- إجابة
-
\(-\dfrac{c+1}{c+2}\)
\(\dfrac{d−16}{16−d}\)
\(\dfrac{7v−35}{25−v^2}\)
- إجابة
-
\(−\dfrac{7}{5+v}\)
\(\dfrac{w^2−3w−28}{49−w^2}\)
ضرب التعبيرات الكسرية وقسمتها
ضرب التعبيرات الكسرية
في التمارين التالية، اضرب.
\(\dfrac{3}{8}·\dfrac{2}{15}\)
- إجابة
-
\(\dfrac{1}{20}\)
\(\dfrac{2xy^2}{8y^3}·\dfrac{16y}{24x}\)
\(\dfrac{3a^2+21a}{a^2+6a−7}·\dfrac{a−1}{ab}\)
- إجابة
-
\(\dfrac{3}{b}\)
\(\dfrac{5z^2}{5z^2+40z+35}·\dfrac{z^2−1}{3z}\)
قسمة التعبيرات الكسرية
في التمارين التالية، قسّم.
\(\dfrac{t^2−4t-12}{t^2+8t+12}÷\dfrac{t^2−36}{6t}\)
- إجابة
-
\(\dfrac{6t}{(t+6)^2}\)
\(\dfrac{r^2−16}{4}÷\dfrac{r^3−64}{2r^2−8r+32}\)
\(\dfrac{11+w}{w−9}÷\dfrac{121−w^2}{9−w}\)
- إجابة
-
\(\dfrac{1}{11+w}\)
\(\dfrac{3y^2−12y−63}{4y+3}÷(6y^2−42y)\)
\(\dfrac{\dfrac{c^2−64}{3c^2+26c+16}}{\dfrac{c^2−4c−32}{15c+10}}\)
- إجابة
-
\(5c+4\)
\(\dfrac{8m^2−8m}{m−4}·\dfrac{m^2+2m−24}{m^2+7m+10}÷\dfrac{2m^2−6m}{m+5}\)
جمع وطرح التعبيرات الكسرية ذات المقام المشترك
جمع التعبيرات الكسرية ذات المقام المشترك
في التمارين التالية، أضف.
\(\dfrac{3}{5}+\dfrac{2}{5}\)
- إجابة
-
\(1\)
\(\dfrac{4a^2}{2a−1}−\dfrac{1}{2a−1}\)
\(\dfrac{p^2+10p}{p+5}+\dfrac{25}{p+5}\)
- إجابة
-
\(p+5\)
\(\dfrac{3x}{x−1}+\dfrac{2}{x−1}\)
اطرح التعبيرات الكسرية ذات المقام المشترك
في التمارين التالية، اطرح.
\(\dfrac{d^2}{d+4}−\dfrac{3d+28}{d+4}\)
- إجابة
-
\(d-7\)
\(\dfrac{z^2}{z+10}−\dfrac{100}{z+10}\)
\(\dfrac{4q^2−q+3}{q^2+6q+5}−\dfrac{3q^2+q+6}{q^2+6q+5}\)
- إجابة
-
\(\dfrac{q−3}{q+5}\)
\(\dfrac{5t+4t+3}{t^2−25}−\dfrac{4t^2−8t−32}{t^2−25}\)
في التمارين التالية، قم بالجمع والطرح.
\(\dfrac{18w}{6w−1}+\dfrac{3w−2}{1−6w}\)
- إجابة
-
\(\dfrac{15w+2}{6w−1}\)
\(\dfrac{a^2+3a}{a^2−4}−\dfrac{3a−8}{4−a^2}\)
\(\dfrac{2b^2+3b−15}{b^2−49}−\dfrac{b^2+16b−1}{49−b^2}\)
- إجابة
-
\(\dfrac{3b−2}{b+7}\)
\(\dfrac{8y^2−10y+7}{2y−5}+\dfrac{2y^2+7y+2}{5−2y}\)
جمع وطرح التعبيرات الكسرية ذات المقامات المختلفة
أوجد المقام المشترك الأصغر للمقادير الكسرية
في التمارين التالية، ابحث عن شاشة LCD.
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\)
- إجابة
-
\((m+2)(m−5)(m+4)\)
\(\dfrac{6}{n^2−4},\quad\dfrac{2n}{n^2−4n+4}\)
\(\dfrac{5}{3p^2+17p−6},\quad\dfrac{2m}{3p^2−23p−8}\)
- إجابة
-
\((3p+1)(p+6)(p+8)\)
في التمارين التالية، أعد الكتابة كمقادير عقلانية مكافئة للقاسم المعطى.
أعد الكتابة كتعبيرات عقلانية مكافئة مع المقام\((m+2)(m−5)(m+4)\)
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\).
أعد الكتابة كتعبيرات عقلانية مكافئة مع المقام\((n−2)(n−2)(n+2)\)
\(\dfrac{6}{n^2−4n+4},\quad\dfrac{2n}{n^2−4}\).
- إجابة
-
\(\dfrac{6n+12}{(n−2)(n−2)(n+2)},\quad\dfrac{2n^2−4n}{(n−2)(n−2)(n+2)}\)
أعد الكتابة كتعبيرات عقلانية مكافئة مع المقام\((3p+1)(p+6)(p+8)\)
\(\dfrac{5}{3p^2+19p+6},\quad\dfrac{7p}{3p^2+25p+8}\)
في التمارين التالية، أضف.
\(\dfrac{2}{3}+\dfrac{3}{5}\)
- إجابة
-
\(\dfrac{19}{15}\)
\(\dfrac{7}{5a}+\dfrac{3}{2b}\)
\(\dfrac{2}{c−2}+\dfrac{9}{c+3}\)
- إجابة
-
\(\dfrac{11c−12}{(c−2)(c+3)}\)
\(\dfrac{3d}{d^2−9}+\dfrac{5}{d^2+6d+9}\)
\(\dfrac{2x}{x^2+10x+24}+\dfrac{3x}{x^2+8x+16}\)
- إجابة
-
\(\dfrac{5x^2+26x}{(x+4)(x+4)(x+6)}\)
\(\dfrac{5q}{p^{2}q−p^2}+\dfrac{4q}{q^2−1}\)
في التمارين التالية، اطرح وأضف.
\(\dfrac{3v}{v+2}−\dfrac{v+2}{v+8}\)
- إجابة
-
\(\dfrac{2(v^2+10v−2)}{(v+2)(v+8)}\)
\(\dfrac{−3w−15}{w^2+w−20}−\dfrac{w+2}{4−w}\)
\(\dfrac{7m+3}{m+2}−5\)
- إجابة
-
\(\dfrac{2m−7}{m+2}\)
\(\dfrac{n}{n+3}+\dfrac{2}{n−3}−\dfrac{n−9}{n^2−9}\)
\(\dfrac{8d}{d^2−64}−\dfrac{4}{d+8}\)
- إجابة
-
\(4d−8\)
\(\dfrac{5}{12x^{2}y}+\dfrac{7}{20xy^3}\)
تبسيط التعبيرات النسبية المعقدة
قم بتبسيط مقدار نسبي معقد بكتابته في صورة قسمة
في التمارين التالية، قم بالتبسيط.
\(\dfrac{\dfrac{5a}{a+2}}{\dfrac{10a^2}{a^2−4}}\)
- إجابة
-
\(\dfrac{a−2}{2a}\)
\(\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}\)
\(\dfrac{x−\dfrac{3x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x−5}}\)
- إجابة
-
\(\dfrac{(x−8)(x−5)}{2}\)
\(\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}−\dfrac{1}{n}}\)
في التمارين التالية، قم بالتبسيط.
\(\dfrac{6+\dfrac{2}{q−4}}{\dfrac{5}{q}+4}\)
- إجابة
-
\(\dfrac{(q−2)(q+4)}{5(q−4)}\)
\(\dfrac{\dfrac{3}{a^2}−\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^2}}\)
\(\dfrac{\dfrac{2}{z^2−49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z−7}}\)
- إجابة
-
\(\dfrac{z−5}{21z+21}\)
\(\dfrac{\dfrac{3}{y^2−4y−32}}{\dfrac{2}{y−8}+\dfrac{1}{y+4}}\)
حل المعادلات الكسرية
حل المعادلات الكسرية
في التمارين التالية، قم بحل.
\(\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}\)
- إجابة
-
\(\dfrac{6}{7}\)
\(1−\dfrac{2}{m}=\dfrac{8}{m^2}\)
\(\dfrac{1}{b−2}+\dfrac{1}{b+2}=\dfrac{3}{b^2−4}\)
- إجابة
-
\(\dfrac{3}{2}\)
\(\dfrac{3}{q+8}−\dfrac{2}{q−2}=1\)
\(\dfrac{v−15}{v^2−9v+18}=\dfrac{4}{v−3}+\dfrac{2}{v−6}\)
- إجابة
-
لا يوجد حل
\(\dfrac{z}{12}+\dfrac{z+3}{3z}=\dfrac{1}{z}\)
حل معادلة نسبية لمتغير معين
في التمارين التالية، قم بحل المتغير المشار إليه.
\(\dfrac{V}{l}=hw\)من أجل\(l\)
- إجابة
-
\(l=\dfrac{V}{hw}\)
\(\dfrac{1}{x}−\dfrac{2}{y}=5\)من أجل\(y\)
\(x=\dfrac{y+5}{z−7}\)من أجل\(z\)
- إجابة
-
\(z=\dfrac{y+5+7x}{x}\)
\(P=\dfrac{k}{V}\)من أجل\(V\)
حل تشابه تطبيقات النسبة والأشكال المتشابهة
حل النسب
في التمارين التالية، قم بحل.
\(\dfrac{x}{4}=\dfrac{3}{5}\)
- إجابة
-
\(\dfrac{12}{5}\)
\(\dfrac{3}{y}=\dfrac{9}{5}\)
\(\dfrac{s}{s+20}=\dfrac{3}{7}\)
- إجابة
-
\(15\)
\(\dfrac{t−3}{5}=\dfrac{t+2}{9}\)
في التمارين التالية، قم بالحل باستخدام النسب.
تناولت راشيل\(21\) أوقية من مخفوق الفراولة يحتوي على\(739\) سعرات حرارية. كم عدد السعرات الحرارية الموجودة في المخفوق\(32\) بالأونصة؟
- إجابة
-
\(1161\)سعرات حرارية
ذهب ليو إلى المكسيك خلال عطلة عيد الميلاد وقام بتحويل\($525\) الدولارات إلى البيزو المكسيكي. في ذلك الوقت، كان سعر الصرف\($1\) الأمريكي يساوي البيزو\(16.25\) المكسيكي. كم عدد البيزو المكسيكي الذي حصل عليه لرحلته؟
في التمارين التالية، قم بحل.
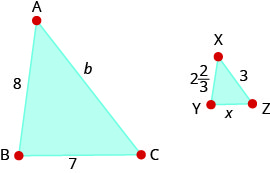
\(∆ABC\)يشبه\(∆XYZ\). يوضح الشكل أطوال ضلعي كل مثلث. أوجد أطوال الضلع الثالث.
- إجابة
-
\(b=9\)؛\(x=2\dfrac{1}{3}\)
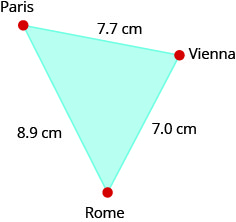
على خريطة أوروبا، تشكل باريس وروما وفيينا مثلثًا تظهر أضلاعه في الشكل أدناه. إذا كانت المسافة الفعلية من روما إلى فيينا هي\(700\) أميال، فأوجد المسافة من
- (أ) من باريس إلى روما
- (ب) من باريس إلى فيينا
يبلغ طول توني\(5.75\) قدمًا. في وقت متأخر بعد ظهر أحد الأيام، كان ظله بطول\(8\) أقدام. في نفس الوقت، كان ظل شجرة قريبة بطول\(32\) أقدام. أوجد ارتفاع الشجرة.
- إجابة
-
\(23\)أقدام
يبلغ ارتفاع منارة في بينساكولا بولاية فلوريدا\(150\) قدمًا. واقفة بجانب التمثال،\(5.5\) ألقت ناتالي التي يبلغ طولها\(1.1\) قدمًا بظلالها على القدم إلى متى سيظل ظل المنارة؟
حل مشاكل الحركة الموحدة وتطبيقات العمل
حل تطبيقات الحركة الموحدة
في التمارين التالية، قم بحل.
عند العودة إلى المنزل لمدة 5 ساعات من زيارة والديها، واجهت ليزا طقسًا سيئًا. كانت قادرة على القيادة\(176\) لأميال بينما كان الطقس جيدًا، ولكن بعد ذلك كانت تقود السيارة\(10\) بشكل أبطأ، وذهبت\(81\) لأميال في الطقس السيئ. ما مدى سرعة قيادتها عندما كان الطقس سيئًا؟
- إجابة
-
45 ميلا في الساعة
يركب مارك طائرة يمكنها الطيران\(490\) لأميال مع رياح خلفية\(20\) تبلغ ميل في الساعة في نفس الوقت الذي يمكنها فيه الطيران\(350\) لأميال مقابل رياح خلفية تبلغ\(20\) ميل في الساعة. ما سرعة الطائرة؟
يمكن لجون ركوب دراجته\(8\) بسرعة أكبر من ركوب لوك دراجته. يستغرق لوقا\(3\) ساعات أطول من جون لركوب\(48\) الأميال. ما مدى السرعة التي يمكن أن يركب بها جون دراجته؟
- إجابة
-
\(16\)ميل بالساعة
كان مارك يتدرب على الترياتلون. ركض\(8\) كيلومترات وقاد الدراجات لمسافة\(32\) كيلومترات في إجمالي\(3\) ساعات. كانت سرعته في الجري أقل\(8\) بالكيلومترات في الساعة من سرعة ركوب الدراجات. ما هي سرعته في الجري؟
في التمارين التالية، قم بحل.
يمكن لجيري تأطير الغرفة في\(1\) ساعة، بينما يستغرق جيك\(4\) ساعات. إلى متى يمكنهم تأطير غرفة تعمل معًا?
- إجابة
-
\(\dfrac{4}{5}\)ساعة
تستغرق ليزا\(3\) ساعات لقص العشب بينما تستغرق ابنة عمها بارب\(2\) ساعات. كم من الوقت سيستغرقون العمل معًا؟
يمكن لجيفري طلاء منزل في\(6\) أيام، ولكن إذا حصل على مساعد يمكنه القيام بذلك في\(4\) غضون أيام. كم من الوقت سيستغرق المساعد لطلاء المنزل بمفرده؟
- إجابة
-
\(12\)أيام
تعمل سو وديب معًا في كتابة كتاب يستغرق\(90\) أيامًا. إذا عملت سو بمفردها فسوف يستغرق الأمر\(120\) أيامها. كم من الوقت ستستغرق ديب لكتابة الكتاب بمفردها?
استخدم التغيير المباشر والعكسي
حل مشاكل التباين المباشر
في التمارين التالية، قم بحل.
\(y\)ويختلف\(x\) ذلك بشكل مباشر عن متى\(y=9\) ومتى\(x=3\)\(x\) ومتى\(y=21\).
- إجابة
-
\(7\)
\(y\)ويختلف\(x\) ذلك بشكل مباشر عن متى\(y=20\) ومتى\(x=2\)\(y\) ومتى\(x=4\).
\(m\)يختلف هذا العدد عكسيًا مع المربع الخاص بـ\(n\)،\(m=4\) ومتى\(n=6\)، والعثور على\(m\) الوقت\(n=2\).
- إجابة
-
\(36\)
فانيسا تسافر لرؤية خطيبها. المسافة\(d\)، تختلف بشكل مباشر مع السرعة\(v\)، فهي تقود. إذا سافرت\(258\) أميالًا بالسيارة في\(60\) الساعة, إلى أي مدى ستسافر\(70\) بسرعة ميل في الساعة?
إذا كانت تكلفة البيتزا تختلف بشكل مباشر مع قطرها، وإذا كانت تكلفة البيتزا\(8\) «قطرها»\($12\)، فكم تبلغ تكلفة\(6\) «قطر البيتزا»؟
- إجابة
-
\($9\)
تختلف مسافة إيقاف السيارة بشكل مباشر مع مربع سرعتها. يستغرق الأمر\(200\) قدمًا لإيقاف السيارة عن السير\(50\) في الساعة. كم عدد الأقدام التي سيستغرقها إيقاف السيارة عن السير\(60\) في الساعة?
في التمارين التالية، قم بحل.
يختلف عدد تذاكر حملة جمع التبرعات الموسيقية بشكل عكسي مع سعر التذاكر. إذا كان لدى Madelyn ما يكفي من المال لشراء\(12\) التذاكر\($6\)، فكم عدد التذاكر التي يمكن لـ Madelyn تحمل شرائها إذا ارتفع السعر إلى\($8\)؟
- إجابة
-
\(97\)تذاكر
في الآلة الوترية، يختلف طول الخيط عكسيًا مع تردد اهتزازاته. إذا كان\(11\) عدد\(360\) الدورات في الثانية لخيط طوله بوصة على كمان، فما التردد الذي يحتويه الخيط الذي\(12\) يبلغ طوله سنتيمتر واحد؟
اختبار الممارسة
في التمارين التالية، قم بالتبسيط.
\(\dfrac{3a^{2}b}{6ab^2}\)
- إجابة
-
\(\dfrac{a}{2b}\)
\(\dfrac{5b−25}{b^2−25}\)
في التمارين التالية، قم بإجراء العملية المشار إليها وتبسيطها.
\(\dfrac{4x}{x+2}·\dfrac{x^2+5x+6}{12x^2}\)
- إجابة
-
\(\dfrac{x+3}{3x}\)
\(\dfrac{5y}{4y−8}·\dfrac{y^2−4}{10}\)
\(\dfrac{4p}{q}+\dfrac{5}{p}\)
- إجابة
-
\(\dfrac{4+5q}{pq}\)
\(\dfrac{1}{z−9}−\dfrac{3}{z+9}\)
\(\dfrac{\dfrac{2}{3}+\dfrac{3}{5}}{\dfrac{2}{5}}\)
- إجابة
-
\(\dfrac{19}{16}\)
\(\dfrac{\dfrac{1}{m}−\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}\)
في التمارين التالية، قم بحل كل معادلة.
\(\dfrac{1}{2}+\dfrac{2}{7}=\dfrac{1}{x}\)
- إجابة
-
\(x = \dfrac{14}{11}\)
\(\dfrac{5}{y−6}=\dfrac{3}{y+6}\)
\(\dfrac{1}{z−5}+\dfrac{1}{z+5}=\dfrac{1}{z^2−25}\)
- إجابة
-
\(z = \dfrac{1}{2}\)
\(\dfrac{t}{4}=\dfrac{3}{5}\)
\(\dfrac{2}{r−2}=\dfrac{3}{r−1}\)
- إجابة
-
\(r = 4\)
في التمارين التالية، قم بحل.
\(y\)يختلف بشكل مباشر مع\(x=5\) ومتى\(x\)\(y=30\)، ابحث عن\(x\) الوقت\(y=42\).
إذا كانت\(y\) تختلف عكسيًا مع\(x\)\(x=6\) الوقت والوقت\(y=20\)، فابحث عن\(y\) الوقت\(x=2\).
- إجابة
-
\(y=60\)
إذا كان\(y\) يختلف عكسيًا مع المربع\(x\)\(x=3\) ووقت حدوثه\(y=9\)، فأوجد\(y\) الوقت\(x=4\).
جرعة الاريثروميسين الموصى بها للكلاب هي\(5\) ملغ لكل رطل يزن الكلب. إذا كانت ديزي\(25\) تزن رطلًا، فكم مليغرام من الإريثروميسين يجب أن يصفه الطبيب البيطري؟
- إجابة
-
\(125\)ملغ
أمضت جوليا\(4\) ساعات بعد ظهر الأحد في ممارسة الرياضة في صالة الألعاب الرياضية. ركضت على جهاز الجري\(10\) لأميال ثم ركبت الدراجة\(20\) لأميال. كانت سرعة دراجتها في الدراجات أسرع\(5\) ميلاً في الساعة من سرعة ركضها على جهاز الجري. ما هي سرعة ركضها؟
يمكن لكيرت ركوب دراجته\(30\) لأميال مع الريح في نفس الفترة الزمنية التي يمكنه فيها\(21\) قطع أميال ضد الرياح. إذا كانت سرعة الرياح\(6\) ميل في الساعة، فما سرعة كورت على دراجته؟
- إجابة
-
\(14\)ميل بالساعة
تهرول أماندا إلى المنتزه\(8\) بأميال باستخدام طريق واحد ثم تعود عبر\(14\) طريق طوله ميل. تستغرق رحلة العودة\(1\) ساعة أطول من هرولها إلى الحديقة. ابحث عن معدل الركض الخاص بها.
يمكن لغسالة النوافذ ذات الخبرة غسل جميع النوافذ في منزل مايك في\(2\) ساعات، بينما يمكن للمتدرب الجديد غسل جميع النوافذ في\(7\) ساعات. كم من الوقت سيستغرق عملهم معًا?
- إجابة
-
\(1\frac{5}{9}\)ساعة
يمكن لجوش تقسيم حمولة شاحنة من جذوع الأشجار في\(8\) ساعات، ولكن بالعمل مع والده يمكنهم إنجاز ذلك في\(3\) ساعات. كم من الوقت سيستغرق والد جوش في العمل بمفرده لتقسيم السجلات?
يختلف السعر الذي يدفعه تايلر مقابل الغاز بشكل مباشر مع عدد الجالونات التي يشتريها. إذا كلفه\(24\) الجالونات\($59.76\)، فما هي تكلفة\(30\) الجالونات؟
- إجابة
-
\($74.70\)
يختلف حجم الغاز في الحاوية بشكل عكسي مع الضغط على الغاز. إذا كانت حاوية النيتروجين تحتوي على كمية\(29.5\) لترات تحتوي على\(2000\) psi، فما الحجم إذا كان الخزان يحتوي على تصنيف\(14.7\) psi؟ قرِّب لأقرب عدد صحيح.
تشكل مدن دايتون وكولومبوس وسينسيناتي مثلثًا في جنوب أوهايو، كما هو موضح في الشكل أدناه، يوضح مسافات الخريطة بين هذه المدن بالبوصة.
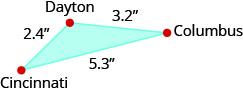
المسافة الفعلية من دايتون إلى سينسيناتي هي\(48\) أميال. ما هي المسافة الفعلية بين دايتون وكولومبوس؟
- إجابة
-
\(64\)أميال