6.5: تقسيم الموحدين

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• قم بتبسيط التعبيرات باستخدام خاصية حاصل القسمة للأسس
• قم بتبسيط التعبيرات باستخدام أسس صفرية
• قم بتبسيط التعبيرات باستخدام حاصل القسمة إلى خاصية الطاقة
• قم بتبسيط التعبيرات بتطبيق العديد من الخصائص
• اقسم الموحدين

ملاحظة

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. قم بالتبسيط:\(\dfrac{8}{24}\).
   إذا فاتتك هذه المشكلة، راجع التمرين 1.6.4.
2. قم بالتبسيط:\((2m^3)^5\).
   إذا فاتتك هذه المشكلة، راجع التمرين 6.2.22.
3. التبسيط:\(\dfrac{12x}{12y}\)
   إذا فاتتك هذه المشكلة، راجع التمرين 1.6.10.

قم بتبسيط التعبيرات باستخدام خاصية خارج القسمة للأسس

في وقت سابق من هذا الفصل، قمنا بتطوير خصائص أسس الضرب. نحن نلخص هذه الخصائص أدناه.

ملخص الخصائص الأسية لعملية الضرب

إذا كانت a و b أرقامًا حقيقية، و m و n هي أرقام صحيحة، إذن

\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]

الآن سننظر إلى الخصائص الأسية للقسمة. قد يساعد التحديث السريع للذاكرة قبل أن نبدأ. لقد تعلمت تبسيط الكسور عن طريق قسمة العوامل المشتركة من البسط والمقام باستخدام خاصية الكسور المتكافئة. ستساعدك هذه الخاصية أيضًا في التعامل مع الكسور الجبرية - والتي تعد أيضًا خارج القسمة.

خاصية الكسور المتكافئة

إذا كانت a و b و c عبارة عن أرقام صحيحة، فأين\(b\neq 0,c\neq 0\).

\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]

كما كان الحال من قبل، سنحاول اكتشاف عقار من خلال النظر في بعض الأمثلة.

\[\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\]

لاحظ أنه في كل حالة كانت القواعد هي نفسها وقمنا بطرح الأسس.

عندما كان الأس الأكبر في البسط، كانت هناك عوامل في البسط.

عندما كان الأس الأكبر في المقام، تُركت لدينا عوامل في القاسم - لاحظ البسط 1.

نحن نكتب:

\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3-2}}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]

يؤدي هذا إلى خاصية حاصل القسمة للأسس.

خاصية القسمة للأسس

إذا كان a رقمًا حقيقيًا\(a\neq 0\)، و m و n عبارة عن أرقام صحيحة، إذن

\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]

قد تساعد بعض الأمثلة مع الأرقام في التحقق من هذه الخاصية.

\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]

التمارين\(\PageIndex{1}\)

قم بالتبسيط:

1. \(\dfrac{x^{9}}{x^{7}}\)
2. \(\dfrac{3^{10}}{3^{2}}\)

إجابة

لتبسيط التعبير باستخدام حاصل القسمة، نحتاج أولاً إلى مقارنة الأسس في البسط والمقام.

1.

منذ 9> 7، هناك المزيد من عوامل x في البسط.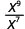
استخدم خاصية حاصل القسمة،\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\)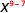
قم بالتبسيط.	\(x^2\)

2.

منذ 10 > 2، هناك المزيد من عوامل x في البسط.
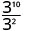
استخدم خاصية حاصل القسمة،\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\)
قم بالتبسيط.	\(3^8\)

لاحظ أنه عندما يكون الأس الأكبر في البسط، تُترك لنا العوامل في البسط.

التمارين\(\PageIndex{2}\)

قم بالتبسيط:

1. \(\dfrac{x^{15}}{x^{10}}\)
2. \(\dfrac{6^{14}}{6^{5}}\)

إجابة

1. \(x^{5}\)
2. \(6^9\)

التمارين\(\PageIndex{3}\)

قم بالتبسيط:

1. \(\dfrac{y^{43}}{y^{37}}\)
2. \(\dfrac{10^{15}}{10^{7}}\)

إجابة

1. \(y^{6}\)
2. \(10^8\)

التمارين\(\PageIndex{4}\)

قم بالتبسيط:

1. \(\dfrac{b^{8}}{b^{12}}\)
2. \(\dfrac{7^{3}}{7^{5}}\)

إجابة

لتبسيط التعبير باستخدام حاصل القسمة، نحتاج أولاً إلى مقارنة الأسس في البسط والمقام.

1.

منذ 12 > 8، يوجد المزيد من عوامل b في المقام.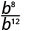
استخدم خاصية حاصل القسمة،\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)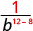
قم بالتبسيط.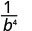

2.

منذ 5 > 3، يوجد المزيد من عوامل العدد 3 في المقام.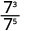
استخدم خاصية حاصل القسمة،\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)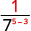
قم بالتبسيط.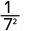
قم بالتبسيط.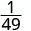

لاحظ أنه عندما يكون الأس الأكبر في المقام، تُترك العوامل في المقام.

التمارين\(\PageIndex{5}\)

قم بالتبسيط:

1. \(\dfrac{x^{18}}{x^{22}}\)
2. \(\dfrac{12^{15}}{12^{30}}\)

إجابة

1. \(\dfrac{1}{x^{4}}\)
2. \(\dfrac{1}{12^{15}}\)

التمارين\(\PageIndex{6}\)

قم بالتبسيط:

1. \(\dfrac{m^{7}}{m^{15}}\)
2. \(\dfrac{9^{8}}{9^{19}}\)

إجابة

1. \(\dfrac{1}{m^{8}}\)
2. \(\dfrac{1}{9^{11}}\)

لاحظ الفرق في المثالين السابقين:

• إذا بدأنا بمزيد من العوامل في البسط، فسوف ننتهي بعوامل في البسط.
• إذا بدأنا بمزيد من العوامل في المقام، فسوف ينتهي بنا الأمر بعوامل في المقام.

الخطوة الأولى في تبسيط التعبير باستخدام خاصية خارج القسمة للأسس هي تحديد ما إذا كان الأس أكبر في البسط أو المقام.

التمارين\(\PageIndex{7}\)

قم بالتبسيط:

1. \(\dfrac{a^{5}}{a^{9}}\)
2. \(\dfrac{x^{11}}{x^{7}}\)

إجابة

1. هل الأس الأكبر في البسط أو المقام؟ نظرًا لوجود 9 > 5، يوجد المزيد من علامات a في المقام، وبالتالي سننتهي بعوامل في المقام.

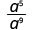
استخدم خاصية حاصل القسمة،\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)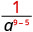
قم بالتبسيط.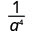

2. لاحظ وجود المزيد من عوامل xx في البسط، منذ 1> 7. لذلك سننتهي بعوامل في البسط.

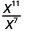
استخدم خاصية حاصل القسمة،\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)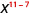
قم بالتبسيط.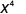

التمارين\(\PageIndex{8}\)

قم بالتبسيط:

1. \(\dfrac{b^{19}}{b^{11}}\)
2. \(\dfrac{z^{5}}{z^{11}}\)

إجابة

1. \(b^{8}\)
2. \(\dfrac{1}{z^{6}}\)

التمارين\(\PageIndex{9}\)

قم بالتبسيط:

1. \(\dfrac{p^{9}}{p^{17}}\)
2. \(\dfrac{w^{13}}{w^{9}}\)

إجابة

1. \(\dfrac{1}{p^{8}}\)
2. \(w^{4}\)

قم بتبسيط التعبيرات باستخدام أس الصفر

الحالة الخاصة لخاصية حاصل القسمة هي عندما تكون أسس البسط والمقام متساوية، مثل تعبير مثل\(\dfrac{a^{m}}{a^{m}}\). من عملك السابق مع الكسور، تعرف ما يلي:

\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]

بالكلمات، الرقم المقسوم على نفسه هو 1. لذلك\(\dfrac{x}{x}=1\)، بالنسبة لأي شخص\(x(x\neq 0)\)، لأن أي رقم مقسوم على نفسه هو 1.

توضح لنا خاصية حاصل القسمة للأسس كيفية تبسيط\(\dfrac{a^{m}}{a^{n}}\) متى\(m>n\) ومتى\(n<m\) عن طريق طرح الأسس. ماذا لو\(m=n\)؟

ضع\(\dfrac{8}{8}\) في اعتبارك ما نعرفه هو 1.

\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)

الآن سنقوم بالتبسيط\(\dfrac{a^{m}}{a^{m}}\) بطريقتين لتقودنا إلى تعريف الأس الصفري. بشكل عام، من أجل\(a\neq 0\):

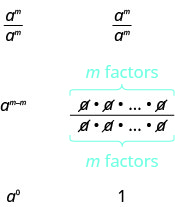
نرى\(\dfrac{a^{m}}{a^{m}}\) التبسيط من\(a^{0}\) وإلى 1. لذا\(a^{0} = 1\).

الأس الصفري

إذا كان الرقم غير صفري، إذن\(a^{0} = 1\).

أي رقم غير صفري يتم رفعه إلى القوة الصفرية هو 1.

في هذا النص، نفترض أن أي متغير نرفعه إلى القوة الصفرية ليس صفرًا.

التمارين\(\PageIndex{10}\)

قم بالتبسيط:

1. \(9^{0}\)
2. \(n^{0}\)

إجابة

يقول التعريف أن أي رقم غير صفري يتم رفعه إلى القوة الصفرية هو 1.

1. \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
2. \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)

التمارين\(\PageIndex{11}\)

قم بالتبسيط:

1. \(15^{0}\)
2. \(m^{0}\)

إجابة

1. 1
2. 1

التمارين\(\PageIndex{12}\)

قم بالتبسيط:

1. \(k^{0}\)
2. \(29^{0}\)

إجابة

1. 1
2. 1

الآن بعد أن حددنا الأس الصفري، يمكننا توسيع جميع خصائص الأسس لتشمل أسس العدد الكامل.

ماذا عن رفع تعبير إلى قوة الصفر؟ دعونا نلقي نظرة على\((2x)^0\). يمكننا استخدام المنتج لقاعدة الطاقة لإعادة كتابة هذا التعبير.

\[\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\]

يخبرنا هذا أن أي تعبير غير صفري يتم رفعه إلى القوة الصفرية هو واحد.

التمارين\(\PageIndex{13}\)

قم بالتبسيط:

1. \((5b)^0\)
2. \((−4a^{2}b)^0\).

إجابة

1. \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
2. \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)

التمارين\(\PageIndex{14}\)

قم بالتبسيط:

1. \((11z)^0\)
2. \((−11pq^{3})^0\).

إجابة

1. 1
2. 1

التمارين\(\PageIndex{15}\)

قم بالتبسيط:

1. \((-6d)^0\)
2. \((−8m^{2}n^{3})^0\).

إجابة

1. 1
2. 1

تبسيط التعبيرات باستخدام حاصل القسمة إلى خاصية القوة

الآن سننظر إلى مثال سيقودنا إلى حاصل القسمة إلى خاصية الطاقة.

\[\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\]

لاحظ أن الأس ينطبق على كل من البسط والمقام.

\[\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\]

يؤدي هذا إلى تحويل حاصل القسمة إلى خاصية القوة للأسس.

حاصل القسمة على خاصية القوة للأسس

إذا كان a و b أرقامًا حقيقية\(b\neq 0\)، و m هو رقم عد، إذن

\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]

لرفع الكسر إلى قوة، ارفع البسط والمقام إلى تلك القوة.

قد يساعدك مثال بالأرقام على فهم هذه الخاصية:

\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]

التمارين\(\PageIndex{16}\)

قم بالتبسيط:

1. \(\left(\dfrac{3}{7}\right)^{2}\)
2. \(\left(\dfrac{b}{3}\right)^{4}\)
3. \(\left(\dfrac{k}{j}\right)^{3}\)

إجابة

1.

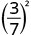
استخدم خاصية حاصل القسمة،\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)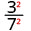
قم بالتبسيط.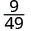

2.

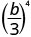
استخدم خاصية حاصل القسمة،\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)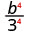
قم بالتبسيط.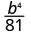

3.

ارفع البسط والمقام إلى القوة الثالثة.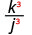

التمارين\(\PageIndex{17}\)

قم بالتبسيط:

1. \(\left(\dfrac{5}{8}\right)^{2}\)
2. \(\left(\dfrac{p}{10}\right)^{4}\)
3. \(\left(\dfrac{m}{n}\right)^{7}\)

إجابة

1. \(\dfrac{25}{64}\)
2. \(\dfrac{p^{4}}{10,000}\)
3. \(\dfrac{m^{7}}{n^{7}}\)

التمارين\(\PageIndex{18}\)

قم بالتبسيط:

1. \(\left(\dfrac{1}{3}\right)^{3}\)
2. \(\left(\dfrac{-2}{q}\right)^{3}\)
3. \(\left(\dfrac{w}{x}\right)^{4}\)

إجابة

1. \(\dfrac{1}{27}\)
2. \(\dfrac{-8}{q^{3}}\)
3. \(\dfrac{w^{4}}{x^{4}}\)

قم بتبسيط التعبيرات بتطبيق العديد من الخصائص

سنقوم الآن بتلخيص جميع خصائص الأسس بحيث يتم تجميعها معًا للإشارة إليها أثناء تبسيط التعبيرات باستخدام العديد من الخصائص. لاحظ أنه تم تعريفها الآن لأسس الأرقام الكاملة.

ملخص خصائص الأس

إذا كانت a و b أرقامًا حقيقية، و m و n هي أرقام صحيحة، إذن

\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]

التمارين\(\PageIndex{19}\)

قم بالتبسيط:\(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)

إجابة

\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)

التمارين\(\PageIndex{20}\)

قم بالتبسيط:\(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)

إجابة

\(m^{13}\)

التمارين\(\PageIndex{21}\)

قم بالتبسيط:\(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)

إجابة

\(k^{5}\)

التمارين\(\PageIndex{22}\)

قم بالتبسيط:\(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)

إجابة

\[\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\]

لاحظ أنه بعد تبسيط المقام في الخطوة الأولى، أصبح البسط والمقام متساويين. لذا فإن القيمة النهائية تساوي 1.

التمارين\(\PageIndex{23}\)

قم بالتبسيط\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\).

إجابة

1

التمارين\(\PageIndex{24}\)

قم بالتبسيط\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\).

إجابة

1

التمارين\(\PageIndex{25}\)

قم بالتبسيط:\(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)

إجابة

\[\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\]

التمارين\(\PageIndex{25}\)

قم بالتبسيط:\(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)

إجابة

\(r^{8}\)

التمارين\(\PageIndex{25}\)

قم بالتبسيط:\(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)

إجابة

\(v^{6}\)

التمارين\(\PageIndex{26}\)

قم بالتبسيط:\(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)

إجابة

هنا لا يمكننا التبسيط داخل الأقواس أولاً، لأن القواعد ليست هي نفسها.

\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)

التمارين\(\PageIndex{27}\)

قم بالتبسيط:\(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)

إجابة

\(\dfrac{a^{12}}{b^{8}}\)

التمارين\(\PageIndex{28}\)

قم بالتبسيط:\(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)

إجابة

\(\dfrac{q^{21}}{r^{15}}\)

التمارين\(\PageIndex{29}\)

قم بالتبسيط:\(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)

إجابة

\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)

التمارين\(\PageIndex{30}\)

قم بالتبسيط:\(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)

إجابة

\(\dfrac{49 x^{6}}{81 y^{2}}\)

التمارين\(\PageIndex{31}\)

قم بالتبسيط:\(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)

إجابة

\(\dfrac{9 x^{8}}{49 v^{2}}\)

التمارين\(\PageIndex{32}\)

قم بالتبسيط:\(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)

إجابة

\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)

التمارين\(\PageIndex{32}\)

قم بالتبسيط:\(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)

إجابة

\(\dfrac{1}{a^{6}}\)

التمارين\(\PageIndex{33}\)

قم بالتبسيط:\(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)

إجابة

\(\dfrac{1}{p^{15}}\)

التمارين\(\PageIndex{34}\)

قم بالتبسيط:\(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)

إجابة

\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)

التمارين\(\PageIndex{35}\)

قم بالتبسيط:\(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)

إجابة

9\(r^{18}\)

التمارين\(\PageIndex{36}\)

قم بالتبسيط:\(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)

إجابة

\(\dfrac{2}{x}\)

تقسيم المونوميال

لقد تعرفت الآن على جميع خصائص الأسس واستخدمتها لتبسيط التعبيرات. بعد ذلك، سترى كيفية استخدام هذه الخصائص لتقسيم القيم الأحادية. ستستخدمها لاحقًا لتقسيم كثيرات الحدود.

التمارين\(\PageIndex{37}\)

ابحث عن حاصل القسمة:\(56 x^{7} \div 8 x^{3}\)

إجابة

\[\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\]

التمارين\(\PageIndex{38}\)

ابحث عن حاصل القسمة:\(42y^{9} \div 6 y^{3}\)

إجابة

\(7y^{6}\)

التمارين\(\PageIndex{39}\)

ابحث عن حاصل القسمة:\(48z^{8} \div 8 z^{2}\)

إجابة

\(6z^{6}\)

التمارين\(\PageIndex{40}\)

ابحث عن حاصل القسمة:\(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)

إجابة

عندما نقسم وحيدات الحد بأكثر من متغير واحد، نكتب كسرًا واحدًا لكل متغير.

\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)

التمارين\(\PageIndex{41}\)

ابحث عن حاصل القسمة:\(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)

إجابة

\(-\dfrac{9}{a^{5} b}\)

التمارين\(\PageIndex{42}\)

ابحث عن حاصل القسمة:\(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)

إجابة

\(\dfrac{-9 d}{c^{4}}\)

التمارين\(\PageIndex{43}\)

ابحث عن حاصل القسمة:\(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)

إجابة

\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)

التمارين\(\PageIndex{44}\)

ابحث عن حاصل القسمة:\(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)

إجابة

\(\dfrac{2 a^{6}}{3 b^{2}}\)

التمارين\(\PageIndex{45}\)

ابحث عن حاصل القسمة:\(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)

إجابة

\(-\dfrac{3 q^{6}}{5 p^{8}}\)

بمجرد التعرف على العملية وممارستها خطوة بخطوة عدة مرات، قد تتمكن من تبسيط جزء في خطوة واحدة.

التمارين\(\PageIndex{46}\)

ابحث عن حاصل القسمة:\(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)

إجابة

كن حذرًا جدًا في التبسيط\(\dfrac{14}{21}\) عن طريق تقسيم عامل مشترك، وتبسيط المتغيرات بطرح أسسها.

\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)

التمارين\(\PageIndex{47}\)

ابحث عن حاصل القسمة:\(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)

إجابة

\(\dfrac{4 y^{2}}{7 x^{4}}\)

التمارين\(\PageIndex{48}\)

ابحث عن حاصل القسمة:\(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)

إجابة

\(\dfrac{5}{8 m^{5} n^{3}}\)

في جميع الأمثلة حتى الآن، لم يكن هناك أي عمل للقيام به في البسط أو المقام قبل تبسيط الكسر. في المثال التالي، سنجد أولاً حاصل ضرب وحدتين في البسط قبل تبسيط الكسر. هذا يتبع ترتيب العمليات. تذكر أن شريط الكسر هو رمز التجميع.

التمارين\(\PageIndex{49}\)

ابحث عن حاصل القسمة:\(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)

إجابة

\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)

التمارين\(\PageIndex{50}\)

ابحث عن حاصل القسمة:\(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)

إجابة

\(2 a b^{2}\)

التمارين\(\PageIndex{51}\)

ابحث عن حاصل القسمة:\(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)

إجابة

\(-4 x y^{5}\)

ملاحظة

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع تقسيم المونوميات:

• التعبيرات العقلانية
• تقسيم الموحدين
• قسمة الموحدين 2

المفاهيم الرئيسية

• خاصية حاصل القسمة للأسس:
  • إذا كان a رقمًا حقيقيًا، و m\(a\neq 0\)، n عبارة عن أرقام صحيحة، فعندئذٍ:\(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
• الأس الصفري
  • إذا كان الرقم غير صفري، إذن\(a^{0} =1\).
• حاصل قسمة خاصية القوة للأسس:
  • إذا كانت a و b أرقامًا حقيقية\(b\neq 0\)، و mm هي رقم عد، فعندئذٍ:\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
  • لرفع الكسر إلى قوة، ارفع البسط والمقام إلى تلك القوة.
• ملخص خصائص الأس
  • إذا كانت a و b عبارة عن أرقام حقيقية و m و nm و n هي أرقام صحيحة، إذن\(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)