5.6: تمثيل أنظمة المتباينات الخطية بيانيًّا
- Page ID
- 200123
في نهاية هذا القسم، ستكون قادرًا على:
- حدِّد ما إذا كان الزوج المُرتَّب حلاً لنظام المتباينات الخطية
- حل نظام المتباينات الخطية بالرسم البياني
- حل تطبيقات أنظمة عدم المساواة
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- رسم بياني x>2 على خط الأعداد.
إذا فاتتك هذه المشكلة، راجع التمرين 2.7.1. - حل عدم المساواة 2a<5a+12.
إذا فاتتك هذه المشكلة، راجع التمرين 2.7.22. - حدد ما إذا كان الزوج\((3,\frac{1}{2})\) المطلوب حلاً للنظام\(\left\{\begin{array}{l}{x+2 y=4} \\ {y=6 x}\end{array}\right.\).
إذا فاتتك هذه المشكلة، راجع التمرين 5.1.1.
حدِّد ما إذا كان الزوج المُرتَّب حلاً لنظام المتباينات الخطية
إن تعريف نظام عدم المساواة الخطية يشبه إلى حد كبير تعريف نظام المعادلات الخطية.
يشكل اثنان أو أكثر من المتباينات الخطية المجمعة معًا نظامًا من عدم المساواة الخطية.
يشبه نظام عدم المساواة الخطية نظامًا من المعادلات الخطية، ولكنه يحتوي على تباينات بدلاً من المعادلات. يظهر أدناه نظام من اثنين من عدم المساواة الخطية.
\[\left\{\begin{array}{l}{x+4 y \geq 10} \\ {3 x-2 y<12}\end{array}\right.\]
لحل نظام عدم المساواة الخطية، سنجد قيم المتغيرات التي تمثل حلولًا لكلا المتباينين. نحل النظام باستخدام الرسوم البيانية لكل عدم مساواة ونعرض الحل كرسم بياني. سنجد المنطقة على متن الطائرة التي تحتوي على جميع الأزواج المرتبة (x، y) (x، y) التي تجعل كلا المتباينين صحيحين.
حلول نظام عدم المساواة الخطية هي قيم المتغيرات التي تجعل جميع التفاوتات صحيحة.
يظهر حل نظام المتباينات الخطية كمنطقة مظللة في نظام الإحداثيات xy الذي يتضمن جميع النقاط التي تجعل أزواجها المرتبة عدم المساواة صحيحة.
لتحديد ما إذا كان الزوج المُرتب حلاً لنظام يتكون من تباينين، فإننا نستبدل قيم المتغيرات في كل تفاوت. إذا كان الزوج الذي تم ترتيبه يجعل كلا المتباينين صحيحين، فهذا حل للنظام.
حدد ما إذا كان الزوج المطلوب حلاً للنظام. \(\left\{\begin{array}{l}{x+4 y \geq 10} \\ {3 x-2 y<12}\end{array}\right.\)
- (−2، 4)
- (3,1)
- إجابة
-
1. هل يمثل الزوج المُرتَّب (−٢، ٤) حلاً؟

جعل الزوج المُرتب (−2، 4) كلا المتباينين حقيقة. لذلك (−2، 4) هو الحل لهذا النظام.
2. هل يعتبر الزوج المطلوب (3,1) حلاً؟

جعل الزوج الذي تم ترتيبه (3,1) أحد أوجه عدم المساواة صحيحًا، بينما جعل الآخر خاطئًا. لذلك (3,1) ليس حلاً لهذا النظام.
حدد ما إذا كان الزوج المطلوب حلاً للنظام. \(\left\{\begin{array}{l}{x-5 y>10} \\ {2 x+3 y>-2}\end{array}\right.\)
- (3، −1)
- (6، −3)
- إجابة
-
- كلا
- نعم
حدد ما إذا كان الزوج المطلوب حلاً للنظام. \(\left\{\begin{array}{l}{y>4 x-2} \\ {4 x-y<20}\end{array}\right.\)
- (2,1)
- (4، −1)
- إجابة
-
- كلا
- كلا
حل نظام المتباينات الخطية عن طريق التمثيل البياني
إن حل عدم المساواة الخطية الواحدة هو المنطقة الموجودة على جانب واحد من خط الحدود التي تحتوي على جميع النقاط التي تجعل عدم المساواة صحيحًا. إن حل نظام المتباينين الخطيين هو المنطقة التي تحتوي على حلول لكلا المتباينين. للعثور على هذه المنطقة، سنقوم برسم بياني لكل عدم مساواة على حدة ثم تحديد المنطقة التي ينطبق فيها كلاهما. يتم عرض الحل دائمًا كرسم بياني.
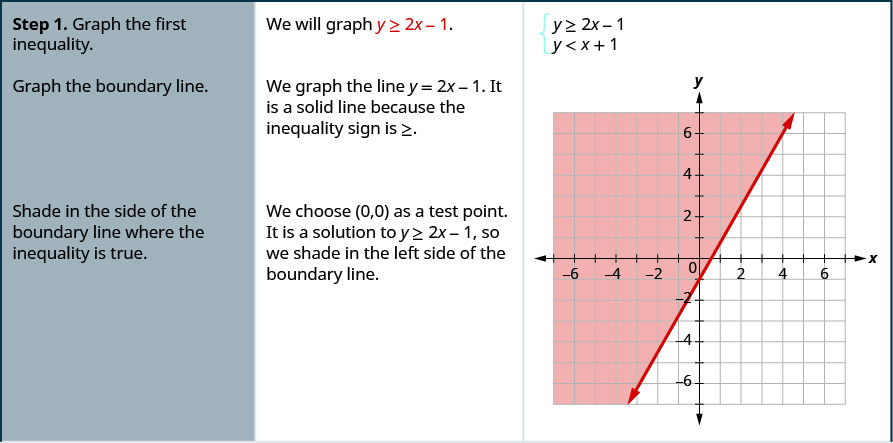
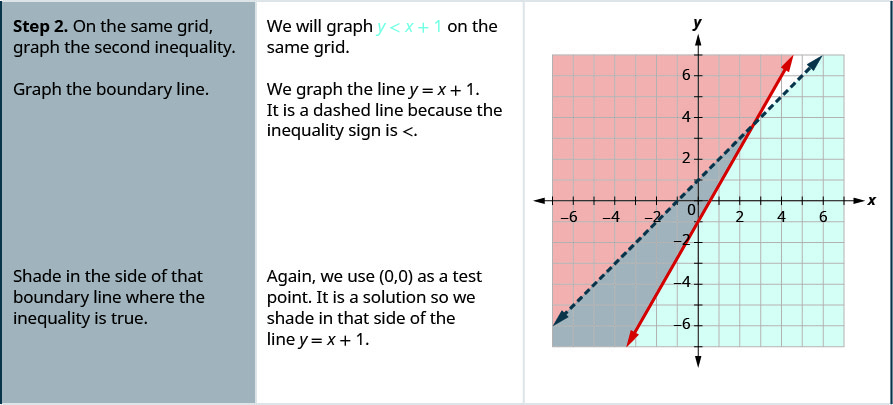
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{y \geq 2 x-1} \\ {y<x+1}\end{array}\right.\)
- إجابة
-


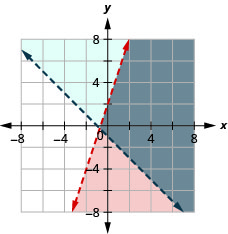
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{y<3 x+2} \\ {y>-x-1}\end{array}\right.\)
- إجابة
-
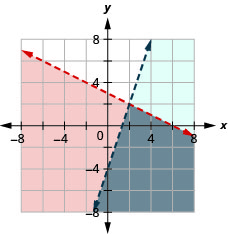
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{y<-\frac{1}{2} x+3} \\ {y<3 x-4}\end{array}\right.\)
- إجابة
-
- رسم بياني لأول عدم مساواة.
- رسم خط الحدود.
- ضع الظل في جانب خط الحدود حيث يكون عدم المساواة صحيحًا.
- على نفس الشبكة، قم برسم عدم المساواة الثانية.
- رسم خط الحدود.
- ضع الظل على جانب خط الحدود هذا حيث يكون عدم المساواة صحيحًا.
- الحل هو المنطقة التي يتداخل فيها التظليل.
- تحقق من ذلك باختيار نقطة اختبار.
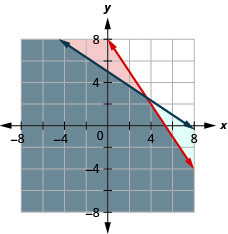
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{x-y>3} \\ {y<-\frac{1}{5} x+4}\end{array}\right.\)
- إجابة
-
الرسم البياني x − y > 3، عن طريق التمثيل البياني x − y = 3
واختبار نقطة.
عمليات الاعتراض هي x = 3 و y = −3 وسوف يكون
خط الحدود متقطعًا.
اختبار (0، 0). إنه يجعل عدم المساواة كاذبًا. لذلك،
قم بتظليل الجانب الذي لا يحتوي على (0، 0) باللون الأحمر.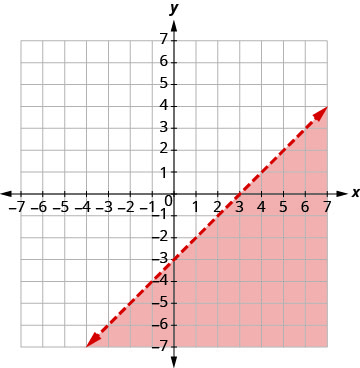
لم يتم تضمين نقطة تقاطع الخطين حيث تم قطع كلا الخطين الحدوديين. الحل هو المنطقة المظللة مرتين وهي المنطقة المظللة الداكنة.الرسم البياني y<−15x+4 عن طريق التمثيل البياني y=−15x+4
باستخدام المنحدر m=−15 وY -التقاطع
b = 4. سيتم قطع خط الحدود.
اختبار (0، 0). يجعل عدم المساواة صحيحًا، لذا قم بتظليل الجانب الذي يحتوي على (0، 0) باللون الأزرق.
اختر نقطة اختبار في الحل وتحقق من أنها حل لكل من حالات عدم المساواة.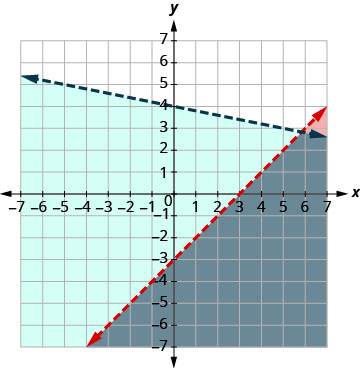
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{x+y \leq 2} \\ {y \geq \frac{2}{3} x-1}\end{array}\right.\)
- إجابة
-
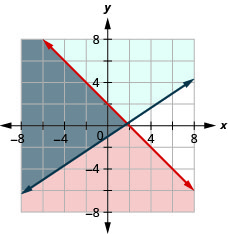
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{3 x-2 y \leq 6} \\ {y>-\frac{1}{4} x+5}\end{array}\right.\)
- إجابة
-
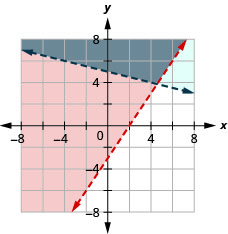
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{x-2 y<5} \\ {y>-4}\end{array}\right.\)
- إجابة
-
الرسم البياني x−2y<5، عن طريق التمثيل البياني x−2y=5 واختبار نقطة.
عمليات الاعتراض هي x = 5 و y = −2.5 وسوف يكون خط الحدود متقطعًا.
اختبار (0، 0). إنه يجعل عدم المساواة حقيقة. لذلك، قم بتظليل الجانب
الذي يحتوي على (0، 0) باللون الأحمر.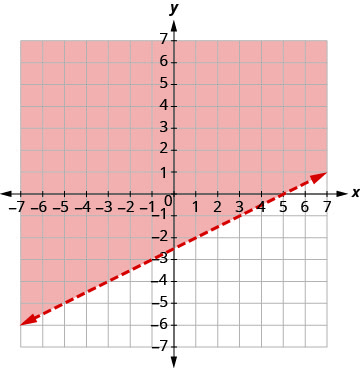
الرسم البياني y > −4، من خلال التمثيل البياني y = −4 والاعتراف بأنه خط
أفقي حتى y = −4. سيتم قطع خط الحدود.
اختبار (0، 0). إنه يجعل عدم المساواة حقيقة. لذلك، قم بتظليل (أزرق)
الجانب الذي يحتوي على (0، 0) باللون الأزرق.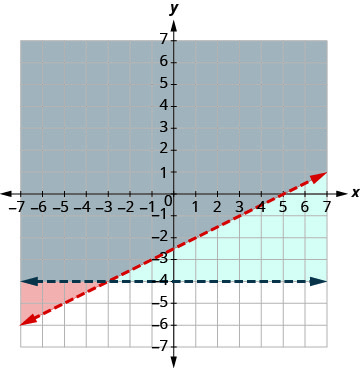
النقطة (0، 0) موجودة في الحل ووجدنا بالفعل أنها حل لكل عدم مساواة. لم يتم تضمين نقطة تقاطع الخطين حيث تم قطع كلا الخطين الحدوديين.
الحل هو المنطقة المظللة مرتين وهي المنطقة المظللة الداكنة.
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{y \geq 3 x-2} \\ {y<-1}\end{array}\right.\)
- إجابة
-
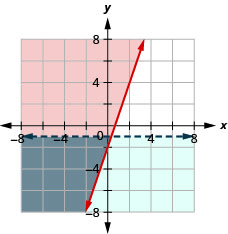
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{x>-4} \\ {x-2 y \leq-4}\end{array}\right.\)
- إجابة
-
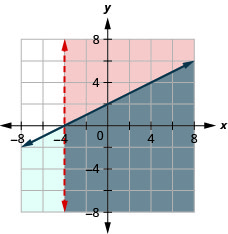
قد لا يكون لأنظمة عدم المساواة الخطية حيث تكون خطوط الحدود متوازية أي حل. سنرى هذا في المثال\(\PageIndex{13}\).
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{4 x+3 y \geq 12} \\ {y<-\frac{4}{3} x+1}\end{array}\right.\)
- إجابة
-
رسم بياني\(4x+3y\geq 12\)، من خلال رسم بياني 4x+3y=12 واختبار نقطة.
عمليات الاعتراض هي x = 3 و y = 4 وسيكون خط الحدود صلبًا.
اختبار (0، 0). إنه يجعل عدم المساواة كاذبًا. لذلك،
قم بتظليل الجانب الذي لا يحتوي على (0، 0) باللون الأحمر.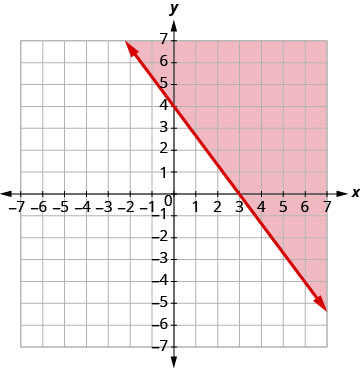
لا توجد نقطة في كلتا المنطقتين المظللتين، لذلك لا يوجد حل للنظام. لا يوجد حل لهذا النظام.رسم بياني\(y<−\frac{4}{3}x+1\) بالرسم البياني\(y=−\frac{4}{3}x+1\) باستخدام
المنحدر\(m = \frac{4}{3}\) ونقطة التقاطع y b = 1. سيتم قطع خط الحدود.
اختبار (0، 0). إنه يجعل عدم المساواة حقيقة. لذلك، قم
بتظليل الجانب الذي يحتوي على (0، 0) باللون الأزرق.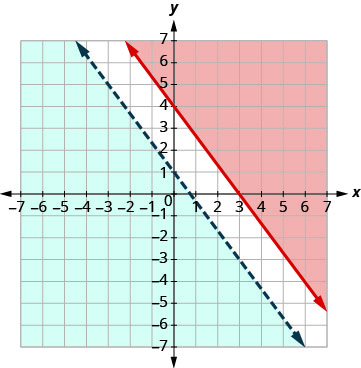
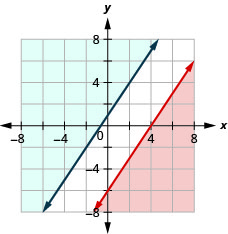
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{3 x-2 y \leq 12} \\ {y \geq \frac{3}{2} x+1}\end{array}\right.\)
- إجابة
-
لا يوجد حل
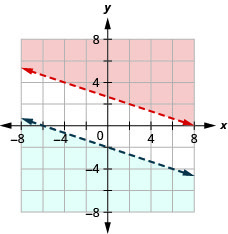
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{x+3 y>8} \\ {y<-\frac{1}{3} x-2}\end{array}\right.\)
- إجابة
-
لا يوجد حل
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{y>\frac{1}{2} x-4} \\ {x-2 y<-4}\end{array}\right.\)
- إجابة
-
رسم بياني\(y>\frac{1}{2}x−4\) من خلال التمثيل البياني\(y=\frac{1}{2}x−4\)
باستخدام المنحدر\(m=\frac{1}{2}\) والجزء المقطوع
b = −4. سيتم قطع خط الحدود.
اختبار (0، 0). إنه يجعل عدم المساواة حقيقة. لذلك، قم
بتظليل الجانب الذي يحتوي على (0، 0) باللون الأحمر.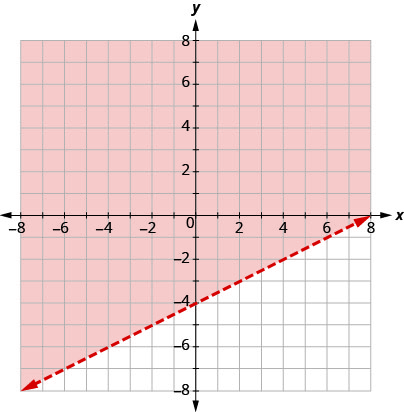
الرسم البياني x−2y<−4x−2y<−4 عن طريق رسم بياني x−2y=−4x−2y=−4 واختبار نقطة.
عمليات الاعتراض هي x = −4 و y = 2 وسوف يكون
خط الحدود متقطعًا.
اختر نقطة اختبار في الحل وتحقق من
أنها حل لكل من حالات عدم المساواة.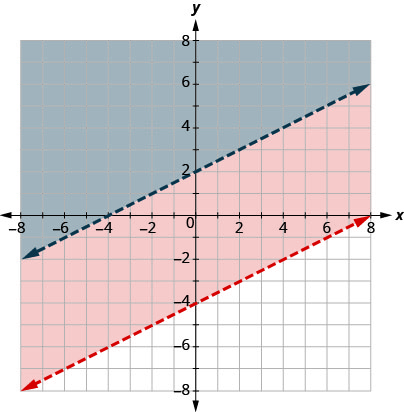
لم يتم تضمين أي نقطة على خطوط الحدود في الحل حيث أن كلا الخطين متقطعان.
الحل هو المنطقة المظللة مرتين، وهي أيضًا الحل لـ x−2y <−4.
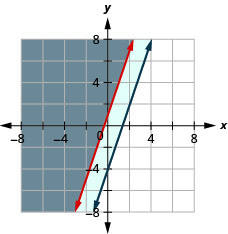
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{y \geq 3 x+1} \\ {-3 x+y \geq-4}\end{array}\right.\)
- إجابة
-
\(y \geq 3 x+1\)
حل النظام عن طريق الرسوم البيانية. \(\left\{\begin{array}{l}{y \leq-\frac{1}{4} x+2} \\ {x+4 y \leq 4}\end{array}\right.\)
- إجابة
-
\(x+4 y \leq 4\)

حل تطبيقات أنظمة عدم المساواة
أول شيء سنحتاج إلى القيام به لحل تطبيقات أنظمة عدم المساواة هو ترجمة كل شرط إلى عدم مساواة. ثم نقوم برسم النظام كما فعلنا أعلاه لرؤية المنطقة التي تحتوي على الحلول. ستكون العديد من المواقف واقعية فقط إذا كان كلا المتغيرين إيجابيين، لذلك ستعرض الرسوم البيانية الربع الأول فقط.
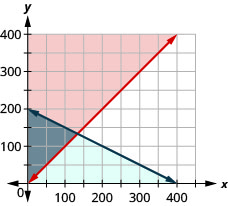
تبيع كريستي صورها في كشك في معرض الشارع. في بداية اليوم، تريد أن يكون لديها 25 صورة على الأقل لعرضها في كشكها. كل صورة صغيرة تعرضها تكلفها 4 دولارات وكل صورة كبيرة تكلفتها 10 دولارات. لا تريد أن تنفق أكثر من 200 دولار على الصور لعرضها.
- اكتب نظامًا من عدم المساواة لنمذجة هذا الموقف.
- رسم بياني للنظام.
- هل يمكنها عرض 15 صورة صغيرة و 5 صور كبيرة؟
- هل يمكنها عرض 3 صور كبيرة و 22 صورة صغيرة؟
- إجابة
-
1. Let x = عدد الصور الصغيرة.
y = عدد الصور الكبيرة
للعثور على نظام عدم المساواة، قم بترجمة المعلومات.
\(\begin{array}{c}{\text { She wants to have at least } 25 \text { photos. }} \\ {\text { The number of small plus the number of large should be at least } 25 .} \\ {x+y \geq 25} \\ {\$ 4 \text { for each small and } \$ 10 \text { for each large must be no more than } \$ 200} \\ {4 x+10 y \leq 200}\end{array}\)
لدينا نظام عدم المساواة الخاص بنا. \(\left\{\begin{array}{l}{x+y \geq 25} \\ {4 x+10 y \leq 200}\end{array}\right.\)2.
للرسم البياني\(x+y\geq 25\)، الرسم البياني x + y = 25 كخط صلب.
اختر (0، 0) كنقطة اختبار. ونظرًا لأنه لا يجعل عدم المساواة
صحيحًا، قم بتظليل الجانب الذي لا يتضمن النقطة (0، 0) باللون الأحمر.
للرسم البياني\(4x+10y\leq 200\)، الرسم البياني 4 × + 10 y = 200 كخط صلب.
اختر (0، 0) كنقطة اختبار. ونظرًا لأنه لا يجعل عدم المساواة
صحيحًا، قم بتظليل الجانب الذي يتضمن النقطة (0، 0) باللون الأزرق.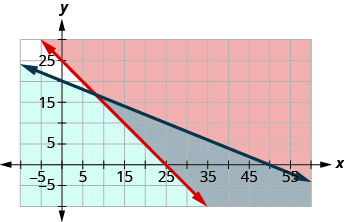
حل النظام هو منطقة الرسم البياني المظللة بشكل مزدوج وبالتالي تكون مظللة باللون الداكن.3. لتحديد ما إذا كانت 10 صور صغيرة و 20 صورة كبيرة ستنجح، نرى ما إذا كانت النقطة (10، 20) موجودة في منطقة الحل. ليس كذلك. لن تعرض كريستي 10 صور صغيرة و 20 صورة كبيرة.
4. لتحديد ما إذا كانت 20 صورة صغيرة و 10 صور كبيرة ستنجح، نرى ما إذا كانت النقطة (20، 10) موجودة في منطقة الحل. إنها كذلك. يمكن أن تختار كريستي عرض 20 صورة صغيرة و 10 صور كبيرة.
لاحظ أنه يمكننا أيضًا اختبار الحلول الممكنة عن طريق استبدال القيم في كل عدم مساواة.
يمكن للمقطورة أن تحمل وزنًا أقصى يبلغ 160 رطلاً وحجمها الأقصى 15 قدمًا مكعبًا. يزن فرن الميكروويف 30 رطلاً وحجمه قدمان مكعبان، بينما تزن الطابعة 20 رطلاً ومساحة 3 أقدام مكعبة.
- اكتب نظامًا من عدم المساواة لنمذجة هذا الموقف.
- رسم بياني للنظام.
- هل يمكن حمل 4 أجهزة ميكروويف وطابعتين على هذه المقطورة؟
- هل يمكن حمل 7 أجهزة ميكروويف و3 طابعات على هذه المقطورة؟
- إجابة
-
- \(\left\{\begin{array}{l}{30 m+20 p \leq 160} \\ {2 m+3 p \leq 15}\end{array}\right.\)
3. نعم
4. لا
تحتاج ماري إلى شراء لوازم من أوراق الإجابة وأقلام الرصاص لإجراء اختبار موحد للصغار في مدرستها الثانوية. يزيد عدد أوراق الإجابة المطلوبة بمقدار 5 على الأقل عن عدد أقلام الرصاص. تكلفة أقلام الرصاص 2 دولار وأوراق الإجابة 1 دولار. تسمح ميزانية ماري لهذه المستلزمات بتكلفة قصوى تبلغ 400 دولار.
- اكتب نظامًا من عدم المساواة لنمذجة هذا الموقف.
- رسم بياني للنظام.
- هل تستطيع ماري شراء 100 قلم رصاص و100 ورقة إجابة؟
- هل تستطيع ماري شراء 150 قلم رصاص و 150 ورقة إجابة؟
- إجابة
-
- \(\left\{\begin{array}{l}{a \geq p+5} \\ {a+2 p \leq 400}\end{array}\right.\)
3. لا
4. لا
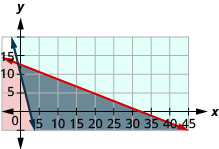
يحتاج عمر إلى تناول 800 سعرة حرارية على الأقل قبل الذهاب إلى تدريبات فريقه. كل ما يريده هو الهامبرغر والبسكويت، ولا يريد أن ينفق أكثر من 5 دولارات. في مطعم الهامبرغر بالقرب من كليته، يحتوي كل هامبرغر على 240 سعرة حرارية ويكلف 1.40 دولارًا. يحتوي كل كوكي على 160 سعرة حرارية ويكلف 0.50 دولارًا.
- اكتب نظامًا من عدم المساواة لنمذجة هذا الموقف.
- رسم بياني للنظام.
- هل يمكن أن يأكل 1 كعكة و 3 هامبرغر؟
- هل يمكنه تناول 4 كعكات و2 هامبرغر؟
- إجابة
-
دعونا h= عدد الهامبرغر.
c = عدد ملفات تعريف الارتباط
للعثور على نظام عدم المساواة، قم بترجمة المعلومات.
يجب أن تكون السعرات الحرارية من الهامبرغر التي تحتوي على 240 سعرة حرارية لكل منها، بالإضافة إلى السعرات الحرارية من الكوكيز التي تحتوي على 160 سعرة حرارية لكل منها أكثر من 800.\[240 h+160 c \geq 800\]
يجب ألا يزيد المبلغ الذي يتم إنفاقه على الهامبرغر بسعر 1.40 دولارًا لكل منهما، بالإضافة إلى المبلغ الذي يتم إنفاقه على ملفات تعريف الارتباط بسعر 0.50 دولارًا لكل منها عن 5.00 دولارًا.
\[1.40 h+0.50 c \leq 5\]
\(\text { We have our system of inequalities. } \quad \left\{\begin{array}{l}{240 h+160 c \geq 800} \\ {1.40 h+0.50 c \leq 5}\end{array}\right.\)
2.
للرسم\(240h+160c\geq 800\) البياني 240h+160c=800 كخط صلب.
اختر (0، 0) كنقطة اختبار. هذا لا يجعل عدم المساواة صحيحًا.
لذلك، قم بتظليل (أحمر) الجانب الذي لا يتضمن النقطة (0، 0).
للرسم البياني\(1.40 h+0.50 c \leq 5\)، الرسم البياني 1.40h+0.50c=5 كخط صلب.
اختر (0,0) كنقطة اختبار. إنه يجعل عدم المساواة حقيقة. لذلك، قم
بتظليل (أزرق) الجانب الذي يتضمن النقطة.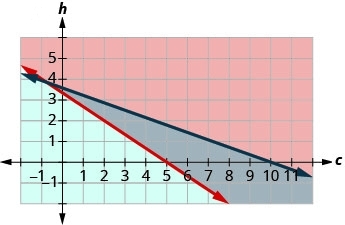
حل النظام هو منطقة الرسم البياني المظللة بشكل مزدوج وبالتالي تكون مظللة باللون الداكن.
3. لتحديد ما إذا كانت كعكة واحدة و3 هامبرغر ستلبي معايير عمر، نرى ما إذا كانت النقطة (1، 3) موجودة في منطقة الحل. ليس كذلك.
4. لتحديد ما إذا كانت 4 ملفات تعريف الارتباط و2 من الهامبرغر ستلبي معايير عمر، نرى ما إذا كانت النقطة (4، 2) موجودة في منطقة الحل. إنها كذلك. قد يختار تناول 4 كعكات و2 هامبرغر.يمكننا أيضًا اختبار الحلول الممكنة عن طريق استبدال القيم في كل عدم مساواة.
يحتاج التوتر إلى تناول 1000 سعر حراري إضافي على الأقل يوميًا للتحضير لسباق الماراثون. لديه 25 دولارًا فقط لإنفاقها على الطعام الإضافي الذي يحتاجه وسوف ينفقه على 0.75 دولارًا من الكعك الذي يحتوي على 360 سعرًا حراريًا لكل منها و 2 دولار من مشروبات الطاقة التي تحتوي على 110 سعرة حرارية.
- اكتب نظامًا من عدم المساواة يمثل هذا الموقف.
- رسم بياني للنظام.
- هل يمكنه شراء 8 دونات و 4 مشروبات طاقة؟
- هل يمكنه شراء 1 دونات و 3 مشروبات طاقة؟
- إجابة
-
- \(\left\{\begin{array}{l}{0.75 d+2 e \leq 25} \\ {360 d+110 e \geq 1000}\end{array}\right.\)
3. نعم
4. لا
أخبره طبيب فيليب أنه يجب أن يضيف ما لا يقل عن 1000 سعر حراري إضافي يوميًا إلى نظامه الغذائي المعتاد. يريد فيليب شراء ألواح بروتين تكلف 1.80 دولارًا لكل منها وتحتوي على 140 سعرًا حراريًا وعصيرًا يكلف 1.25 دولارًا للزجاجة ويحتوي على 125 سعرًا حراريًا. لا يريد أن ينفق أكثر من 12 دولارًا.
- اكتب نظامًا من عدم المساواة يمثل هذا الموقف.
- رسم بياني للنظام.
- هل يمكنه شراء 3 ألواح بروتين و 5 زجاجات عصير؟
- هل يمكنه شراء 5 ألواح بروتين و 3 زجاجات عصير؟
- إجابة
-
- \(\left\{\begin{array}{l}{140 p+125 j \geq 1000} \\ {1.80 p+1.25 j \leq 12}\end{array}\right.\)
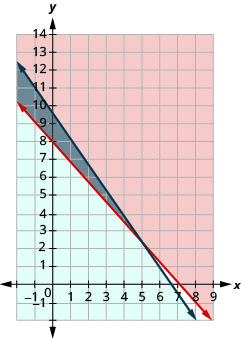
3. نعم
4. لا
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام أنظمة الرسوم البيانية للمتباينات الخطية.
- النظام الرسومي للمتباينات
- أنظمة عدم المساواة
- حل أنظمة المتباينات الخطية عن طريق التمثيل البياني
المفاهيم الرئيسية
- حل نظام المتباينات الخطية عن طريق التمثيل البياني
- رسم بياني لأول عدم مساواة.
- رسم خط الحدود.
- ضع الظل في جانب خط الحدود حيث يكون عدم المساواة صحيحًا.
- على نفس الشبكة، قم برسم عدم المساواة الثانية.
- رسم خط الحدود.
- ضع الظل على جانب خط الحدود هذا حيث يكون عدم المساواة صحيحًا.
- الحل هو المنطقة التي يتداخل فيها التظليل.
- تحقق من ذلك باختيار نقطة اختبار.
- رسم بياني لأول عدم مساواة.
مسرد المصطلحات
- نظام عدم المساواة الخطية
- يشكل اثنان أو أكثر من المتباينات الخطية المجمعة معًا نظامًا من عدم المساواة الخطية.


