5.1: حل أنظمة المعادلات عن طريق التمثيل البياني
- Page ID
- 200145
في نهاية هذا القسم، ستكون قادرًا على:
- حدِّد ما إذا كان الزوج المُرتَّب حلًا لنظام المعادلات
- حل نظام المعادلات الخطية بالرسم البياني
- تحديد عدد حلول النظام الخطي
- حل تطبيقات أنظمة المعادلات بالرسم البياني
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- بالنسبة للمعادلة\(y=\frac{2}{3}x−4\)
ⓐ هل (6,0) حل؟ ⓑ هل (−3، −2) حل؟
إذا فاتتك هذه المشكلة، راجع التمرين 2.1.1. - أوجد المنحدر والجزء المقطوع الصادي للخط 3x−y=12.
إذا فاتتك هذه المشكلة، راجع التمرين 4.5.7. - ابحث عن تقاطعي x و y للخط 2x−3y=12.
إذا فاتتك هذه المشكلة، راجع التمرين 4.3.7.
حدِّد إذا ما كان الزوج المُرتَّب حلًا لنظام المعادلات
في قسم حل المعادلات الخطية والمتباينات، تعلمنا كيفية حل المعادلات الخطية بمتغير واحد. تذكر أن حل المعادلة هو قيمة المتغير الذي يصنع بيانًا صحيحًا عند استبداله بالمعادلة. الآن سنعمل مع أنظمة المعادلات الخطية، معادلتين خطيتين أو أكثر تم تجميعهما معًا.
عندما يتم تجميع معادلتين خطيتين أو أكثر معًا، فإنها تشكل نظامًا من المعادلات الخطية.
سنركز عملنا هنا على أنظمة معادلتين خطيتين في مجهولين. في وقت لاحق، يمكنك حل أنظمة أكبر من المعادلات.
فيما يلي مثال لنظام معادلتين خطيتين. نستخدم قوسًا لإظهار أن المعادلتين مجمعتان معًا لتشكيل نظام من المعادلات.
\[\begin{cases}{2 x+y=7} \\ {x-2 y=6}\end{cases}\]
تحتوي المعادلة الخطية في متغيرين، مثل 2 x + y = 7، على عدد لا نهائي من الحلول. الرسم البياني الخاص به هو خط. تذكر أن كل نقطة على الخط هي حل للمعادلة وكل حل للمعادلة هو نقطة على الخط.
لحل نظام من معادلتين خطيتين، نريد أن نجد قيم المتغيرات التي تمثل حلولًا لكلتا المعادلتين. بمعنى آخر، نحن نبحث عن الأزواج المرتبة (x، y) التي تجعل كلتا المعادلتين صحيحتين. تسمى هذه الحلول لنظام المعادلات.
حلول نظام المعادلات هي قيم المتغيرات التي تجعل جميع المعادلات صحيحة. يتم تمثيل حل نظام من معادلتين خطيتين بزوج مرتب (x، y).
لتحديد ما إذا كان الزوج المرتب حلاً لنظام من معادلتين، فإننا نستبدل قيم المتغيرات في كل معادلة. إذا كان الزوج الذي تم ترتيبه يجعل كلتا المعادلتين صحيحتين، فهذا حل للنظام.
لننظر في النظام أدناه:
\[\begin{cases}{3x−y=7} \\ {x−2y=4}\end{cases}\]
هل يمثل الزوج المُرتَّب (2، −1) حلاً؟
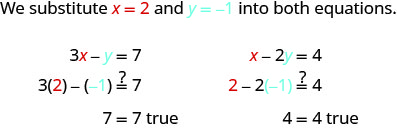
جعل الزوج المُرتَّب (2، −1) كلتا المعادلتين حقيقيتين. لذلك فإن (2، −1) هو الحل لهذا النظام.
دعونا نجرب زوجًا آخر مطلوبًا. هل يعتبر الزوج المطلوب (3، 2) حلاً؟
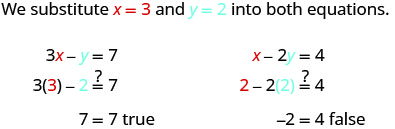
جعل الزوج المُرتب (3، 2) معادلة واحدة صحيحة، لكنه جعل المعادلة الأخرى خاطئة. نظرًا لأنه ليس حلاً لكلتا المعادلتين، فهو ليس حلاً لهذا النظام.
حدد ما إذا كان الزوج المطلوب حلاً للنظام:\(\begin{cases}{x−y=−1} \\ {2x−y=−5}\end{cases}\)
- (−2، −1)
- (−4، −3)
- إجابة
-
1.
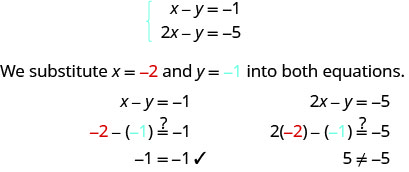
(−2، −1) لا يجعل كلتا المعادلتين حقيقيتين. (−2، −1) ليست حلاً.
2.
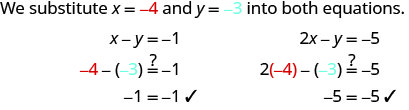
(−4، −3) لا يجعل كلتا المعادلتين حقيقيتين. (−4، −3) هو الحل.
حدد ما إذا كان الزوج المطلوب حلاً للنظام:\(\begin{cases}{3x+y=0} \\ {x+2y=−5}\end{cases}\)
- (1، −3)
- (0,0)
- إجابة
-
- نعم
- كلا
حدد ما إذا كان الزوج المطلوب حلاً للنظام:\(\begin{cases}{x−3y=−8} \\ {−3x−y=4}\end{cases}\)
- (2، −2)
- (−2,2)
- إجابة
-
- كلا
- نعم
حل نظام المعادلات الخطية بالرسم البياني
في هذا الفصل سوف نستخدم ثلاث طرق لحل نظام المعادلات الخطية. الطريقة الأولى التي سنستخدمها هي الرسم البياني. الرسم البياني للمعادلة الخطية هو خط. كل نقطة على الخط هي حل للمعادلة. بالنسبة لنظام مكون من معادلتين، سنرسم خطين. ثم يمكننا رؤية جميع النقاط التي تمثل حلولًا لكل معادلة. ومن خلال إيجاد القواسم المشتركة بين السطور، سنجد الحل للنظام.
تحتوي معظم المعادلات الخطية في متغير واحد على حل واحد، لكننا رأينا أن بعض المعادلات، التي تسمى التناقضات، ليس لها حلول، وبالنسبة للمعادلات الأخرى، التي تسمى الهويات، فإن جميع الأرقام هي حلول. وبالمثل، عندما نحل نظامًا من معادلتين خطيتين يمثلهما رسم بياني من سطرين في نفس المستوى، هناك ثلاث حالات محتملة، كما هو موضح في الشكل\(\PageIndex{1}\):
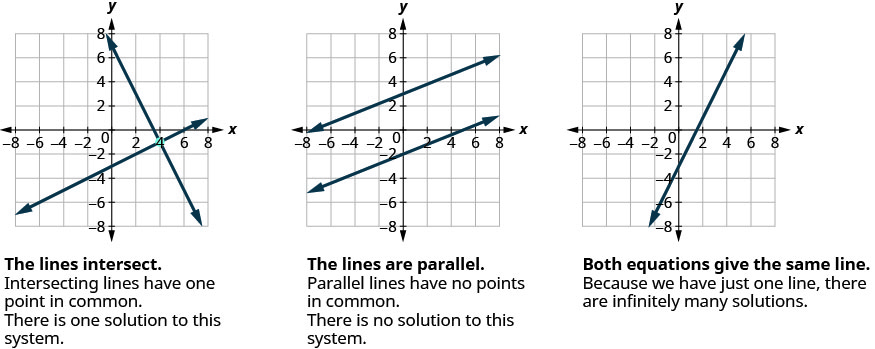
بالنسبة للمثال الأول لحل نظام المعادلات الخطية في هذا القسم وفي القسمين التاليين، سنحل نفس النظام من معادلتين خطيتين. لكننا سنستخدم طريقة مختلفة في كل قسم. بعد رؤية الطريقة الثالثة، ستقرر الطريقة الأكثر ملاءمة لحل هذا النظام.
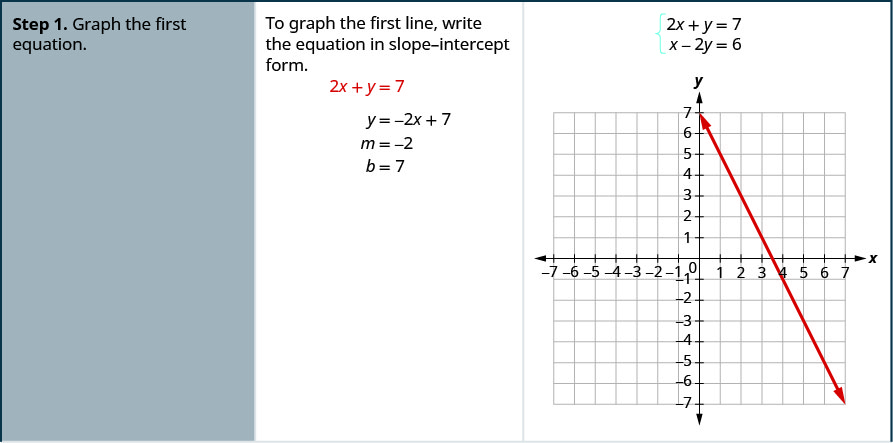
حل النظام عن طريق الرسم البياني:\(\begin{cases}{2x+y=7} \\ {x−2y=6}\end{cases}\)
- إجابة
-


حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{x−3y=−3} \\ {x+y=5}\end{cases}\)
- إجابة
-
(3,2)
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{−x+y=1} \\ {3x+2y=12}\end{cases}\)
- إجابة
-
(2,3)
فيما يلي الخطوات التي يجب استخدامها لحل نظام المعادلات الخطية بالرسوم البيانية.
- ارسم المعادلة الأولى بيانيًا.
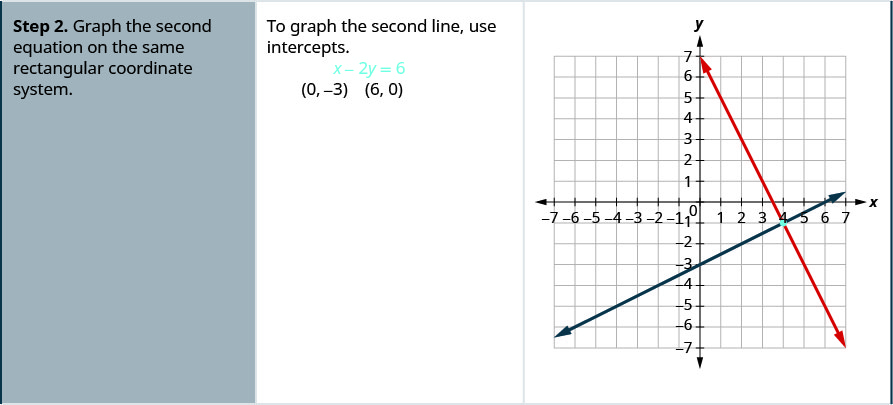
- ارسم المعادلة الثانية على نفس نظام الإحداثيات المستطيلة.
- حدد ما إذا كانت الخطوط تتقاطع أو متوازية أو هي نفس الخط.
- حدد الحل للنظام.
- في حالة تقاطع الخطوط، حدد نقطة التقاطع. تحقق للتأكد من أنه حل لكلتا المعادلتين. هذا هو الحل للنظام.
- إذا كانت الخطوط متوازية، فلن يكون لدى النظام أي حل.
- إذا كانت الخطوط هي نفسها، فإن النظام يحتوي على عدد لا نهائي من الحلول.
حل النظام عن طريق الرسم البياني:\(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)
- إجابة
-
توجد كلتا المعادلتين في هذا النظام في صورة تقاطع منحدر، لذلك سنستخدم منحدرتهما ونقاط التقاطع y لرسم بياني لهما. \(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)
أوجد ميل المعادلة
الأولى وقطعها الصادي.
أوجد ميل المعادلة
الأولى وقطعها الصادي.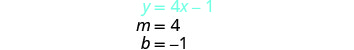
ارسم الخطين بيانيًا. حدد نقطة التقاطع. تتقاطع الخطوط عند (1، 3). 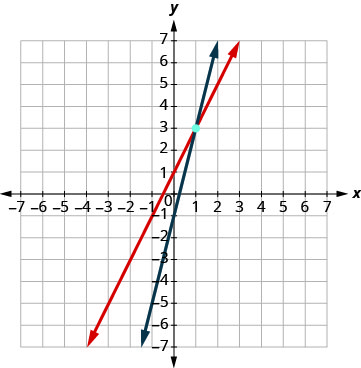
تحقق من الحل في كلتا المعادلتين. \(\begin{array}{l}{y=2 x+1} & {y = 4x - 1}\\{3\stackrel{?}{=}2 \cdot 1+1} &{3\stackrel{?}{=}4 \cdot 1-1} \\ {3=3 \checkmark}&{3=3 \checkmark} \end{array}\) الحل هو (1، 3).
حل النظام عن طريق الرسم البياني:\(\begin{cases}{y=2x+2} \\ {y=-x−4}\end{cases}\)
- إجابة
-
(−2، −2)
حل النظام عن طريق الرسم البياني:\(\begin{cases}{y=3x+3} \\ {y=-x+7}\end{cases}\)
- إجابة
-
(1,6)
\(\PageIndex{7}\)تم إعطاء كلتا المعادلتين في التمرين في شكل منحدر - تقاطع. هذا جعل من السهل علينا رسم الخطوط بسرعة. في المثال التالي، سنقوم أولاً بإعادة كتابة المعادلات في شكل منحدر - مقطع.
حل النظام عن طريق الرسم البياني:\(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)
- إجابة
-
سنحل كلتا المعادلتين لـ yy حتى نتمكن من رسم بياني لهما بسهولة باستخدام منحدراتهما ونقاط التقاطع y. \(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)
حل المعادلة الأولى لـ y.
ابحث عن المنحدر ونقطة التقاطع y.
حل المعادلة الثانية لـ y.
ابحث عن المنحدر ونقطة التقاطع y.\(\begin{aligned} 3 x+y &=-1 \\ y &=-3 x-1 \\ m &=-3 \\ b &=-1 \\ 2 x+y &=0 \\ y &=-2 x \\ b &=0 \end{aligned}\) رسم الخطوط بيانيًا. 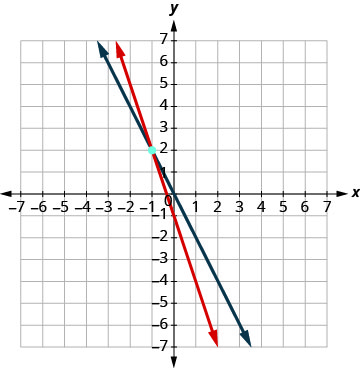
حدد نقطة التقاطع. تتقاطع الخطوط عند (−١، ٢). تحقق من الحل في كلتا المعادلتين. \(\begin{array}{rllrll}{3x+y}&{=}&{-1} & {2x +y}&{=}&{0}\\{3(-1)+ 2}&{\stackrel{?}{=}}&{-1} &{2(-1)+2}&{\stackrel{?}{=}}&{0} \\ {-1}&{=}&{-1 \checkmark}&{0}&{=}&{0 \checkmark} \end{array}\) الحل هو (−1، 2).
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{−x+y=1} \\ {2x+y=10}\end{cases}\)
- إجابة
-
(3,4)
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{ 2x+y=6} \\ {x+y=1}\end{cases}\)
- إجابة
-
(5، −4)
عادة عندما يتم إعطاء المعادلات في شكل قياسي، فإن الطريقة الأكثر ملاءمة لرسمها البياني هي استخدام القطع المقطوعة. سنفعل ذلك في التمرين\(\PageIndex{13}\).
حل النظام عن طريق الرسم البياني:\(\begin{cases}{x+y=2} \\ {x−y=4}\end{cases}\)
- إجابة
-
سنجد التقاطعين x - و y - لكلتا المعادلتين ونستخدمهما لرسم الخطوط.
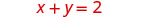
للعثور على عمليات الاعتراض، دع x = 0 وقم بحلها
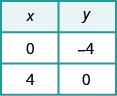
لـ y، ثم اترك y = 0 وقم بحل x.\(\begin{aligned} x+y &=2 \quad x+y=2 \\ 0+y &=2 \quad x+0=2 \\ y &=2 \quad x=2 \end{aligned}\) 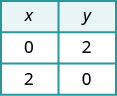
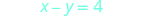
للعثور على عمليات الاعتراض، دع
x = 0 ثم اترك y = 0.\ ابدأ {المصفوفة} {rlr} {x-y} و {=4} و {x-y} و {= 4}\\ {0-y} و {=4} و {x-0} و {=4}\\ {-y} و {=4} و {x} و {=4} و {x} و {=4}\ {y} و {=4}\ مصفوفة النهاية {}
رسم الخط. 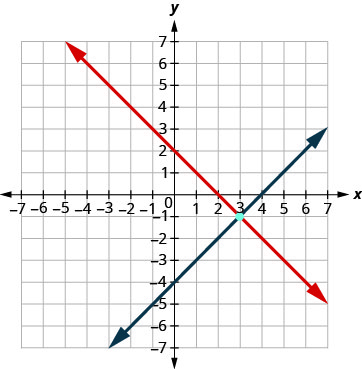
حدد نقطة التقاطع. تتقاطع الخطوط عند (3، −1). تحقق من الحل في كلتا المعادلتين. \(\begin{array}{rllrll}{x+y}&{=}&{2} & {x-y}&{=}&{4}\\{3+(-1)}&{\stackrel{?}{=}}&{2} &{3 - (-1)}&{\stackrel{?}{=}}&{4} \\ {2}&{=}&{2 \checkmark}&{4}&{=}&{4 \checkmark} \end{array}\)
الحل هو (3، −1).
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{x+y=6} \\ {x−y=2}\end{cases}\)
- إجابة
-
(4,2)
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{x+y=2} \\ {x−y=-8}\end{cases}\)
- إجابة
-
(5، −3)
هل تتذكر كيفية رسم معادلة خطية بمتغير واحد فقط؟ سيكون إما خطًا رأسيًا أو أفقيًا.
حل النظام عن طريق الرسم البياني:\(\begin{cases}{y=6} \\ {2x+3y=12}\end{cases}\)
- إجابة
-

نعلم أن المعادلة الأولى تمثل
خطًا أفقيًا قطعه y يساوي ٦.
يتم رسم المعادلة الثانية بسهولة
باستخدام عمليات الاعتراض.
للعثور على عمليات الاعتراض، دع x = 0 ثم y = 0. 
رسم الخطوط بيانيًا. 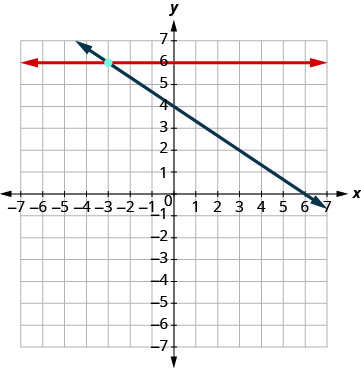
حدد نقطة التقاطع. تتقاطع الخطوط عند (−٣، ٦). تحقق من حل كلتا المعادلتين. \(\begin{array}{rllrll}{y}&{=}&{6} & {2x+3y}&{=}&{12}\\{6}&{\stackrel{?}{=}}&{6} &{2(-3) + 3(6)}&{\stackrel{?}{=}}&{12} \\ {6}&{=}&{6 \checkmark} &{-6+18}&{\stackrel{?}{=}}&{12} \\ {}&{}&{}&{12}&{=}&{12 \checkmark} \end{array}\) الحل هو (−3، 6).
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{y=−1} \\ {x+3y=6}\end{cases}\)
- إجابة
-
(9، −1)
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{x=4} \\ {3x−2y=24}\end{cases}\)
- إجابة
-
(4، −6)
في جميع أنظمة المعادلات الخطية حتى الآن، تقاطعت الخطوط وكان الحل نقطة واحدة. في المثالين التاليين، سننظر إلى نظام المعادلات الذي ليس له حل ونظام المعادلات الذي يحتوي على عدد لا نهائي من الحلول.
حل النظام عن طريق الرسم البياني:\(\begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\)
- إجابة
-
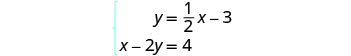
لرسم المعادلة الأولى بيانيًا،
سنستخدم منحدرها والجزء المقطوع من y.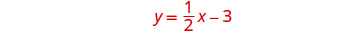
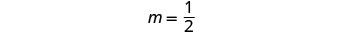
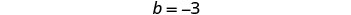
لرسم المعادلة الثانية بيانيًا،
سنستخدم القطع المقطوعة.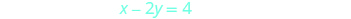
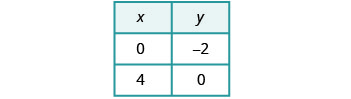
رسم الخطوط بيانيًا. 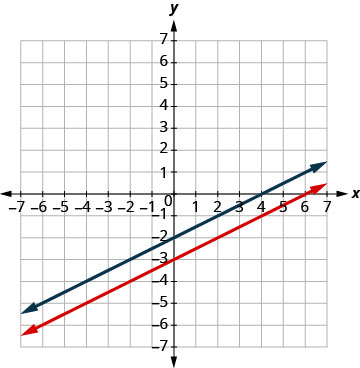
حدد نقطة التقاطع. الخطوط متوازية. نظرًا لعدم وجود نقطة في كلا الخطين، لا يوجد زوج مرتب
يجعل كلا المعادلتين صحيحتين. لا يوجد حل
لهذا النظام.
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{y=-\frac{1}{4}x+2} \\ {x+4y=-8}\end{cases}\)
- إجابة
-
لا يوجد حل
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{y=3x−1} \\ {6x−2y=6}\end{cases}\)
- إجابة
-
لا يوجد حل
حل النظام عن طريق الرسم البياني:\(\begin{cases}{y=2x−3} \\ {−6x+3y=−9}\end{cases}\)
- إجابة
-
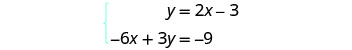
أوجد ميل المعادلة
الأولى وقطعها الصادي.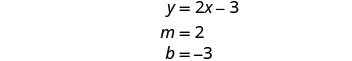
أوجد الأجزاء المقطوعة للمعادلة الثانية. 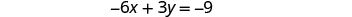
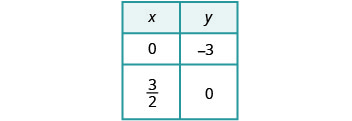
رسم الخطوط بيانيًا. 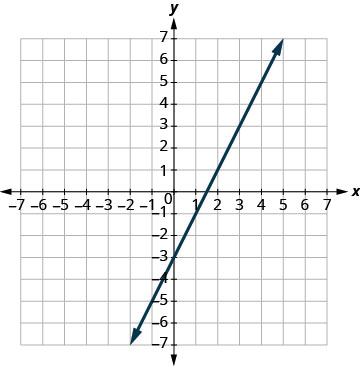
حدد نقطة التقاطع. الخطوط هي نفسها! نظرًا لأن كل نقطة على الخط تجعل المعادلتين
صحيحتين، فهناك عدد لا نهائي من الأزواج المرتبة التي تجعل
كلتا المعادلتين صحيحتين.هناك العديد من الحلول لهذا النظام.
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{y=−3x−6} \\ {6x+2y=−12}\end{cases}\)
- إجابة
-
العديد من الحلول بلا حدود
حل كل نظام عن طريق الرسم البياني:\(\begin{cases}{y=\frac{1}{2}x−4} \\ {2x−4y=16}\end{cases}\)
- إجابة
-
العديد من الحلول بلا حدود
إذا كتبت المعادلة الثانية في التمرين\(\PageIndex{22}\) في صورة تقاطع المنحدر، فقد تدرك أن المعادلات لها نفس الميل ونفس التقاطع y.
عندما قمنا برسم السطر الثاني في المثال الأخير، قمنا برسمه مباشرة فوق السطر الأول. نقول أن الخطين متزامنان. الخطوط المتزامنة لها نفس المنحدر ونفس التقاطع y.
الخطوط المتزامنة لها نفس المنحدر ونفس التقاطع y.
تحديد عدد حلول النظام الخطي
ستكون هناك أوقات نريد فيها معرفة عدد الحلول المتاحة لنظام المعادلات الخطية، ولكن قد لا نضطر في الواقع إلى إيجاد الحل. سيكون من المفيد تحديد ذلك بدون رسم بياني.
لقد رأينا أن خطين في نفس المستوى يجب أن يتقاطعا أو يكونان متوازيين. تحتوي\(\PageIndex{16}\) جميع أنظمة المعادلات في التمرين\(\PageIndex{4}\) من خلال التمرين على خطين متقاطعين. كان لكل نظام حل واحد.
النظام ذو الخطوط المتوازية، مثل\(\PageIndex{19}\) Exercise، ليس له حل. ماذا حدث في التمرين\(\PageIndex{22}\)؟ تحتوي المعادلات على خطوط متزامنة، وبالتالي كان لدى النظام العديد من الحلول بلا حدود.
سننظم هذه النتائج في الشكل\(\PageIndex{2}\) أدناه:
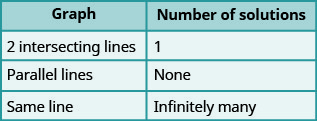
تحتوي الخطوط المتوازية على نفس المنحدر ولكن تقاطعات y مختلفة. لذلك، إذا كتبنا المعادلتين في نظام المعادلات الخطية في شكل منحدر - مقطع، يمكننا أن نرى عدد الحلول التي ستكون موجودة بدون رسم بياني! انظر إلى النظام الذي قمنا بحله في التمرين\(\PageIndex{19}\).
\(\begin{array} {cc} & \begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\\ \text{The first line is in slope–intercept form.} &\text { If we solve the second equation for } y, \text { we get } \\ &x-2 y =4 \\ y = \frac{1}{2}x -3& x-2 y =-x+4 \\ &y =\frac{1}{2} x-2 \\ m=\frac{1}{2}, b=-3&m=\frac{1}{2}, b=-2 \end{array}\)
الخطان لهما نفس المنحدر ولكن تقاطعات y مختلفة. إنها خطوط متوازية.
\(\PageIndex{3}\)يوضح الشكل كيفية تحديد عدد حلول النظام الخطي من خلال النظر إلى المنحدرات والعوارض.
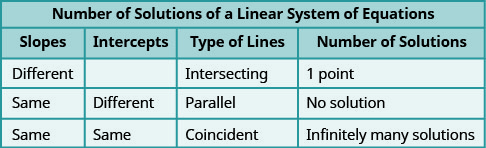
دعونا نلقي نظرة أخرى على معادلاتنا في التمرين\(\PageIndex{19}\) التي أعطتنا خطوطًا متوازية.
\ [\ ابدأ {الحالات} {y=\ frac {1} {2} x−3}\\\ {x−2y=4}\ النهاية {الحالات}\)]
عندما كان كلا الخطين في شكل تقاطع منحدر كان لدينا:
\[y=\frac{1}{2} x-3 \quad y=\frac{1}{2} x-2\]
هل تدرك أنه من المستحيل وجود زوج واحد مرتب (x، y) يمثل حلاً لكل من هاتين المعادلتين؟
نسمي نظامًا من المعادلات مثل هذا نظامًا غير متناسق. ليس لديها حل.
يُطلق على نظام المعادلات الذي يحتوي على حل واحد على الأقل اسم النظام المتسق.
نظام المعادلات المتسق هو نظام معادلات بحل واحد على الأقل.
نظام المعادلات غير المتسق هو نظام معادلات بدون حل.
نقوم أيضًا بتصنيف المعادلات في نظام المعادلات عن طريق تسمية المعادلات بأنها مستقلة أو تابعة. إذا كانت المعادلتين معادلتين مستقلتين، فلكل منهما مجموعة الحلول الخاصة بها. الخطوط المتقاطعة والخطوط المتوازية مستقلة.
في حالة اعتماد معادلتين، فإن جميع حلول المعادلة الواحدة هي أيضًا حلول للمعادلة الأخرى. عندما نرسم معادلتين تابعتين، نحصل على خطوط متزامنة.
هناك معادلتان مستقلتان إذا كانت لهما حلول مختلفة.
تعتمد معادلتان إذا كانت جميع حلول المعادلة الواحدة هي أيضًا حلول للمعادلة الأخرى.
دعونا نلخص ذلك من خلال النظر إلى الرسوم البيانية للأنواع الثلاثة من الأنظمة. انظر الشكل\(\PageIndex{4}\) والشكل\(\PageIndex{5}\).
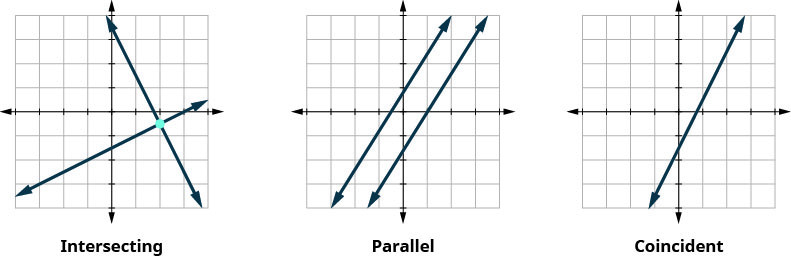
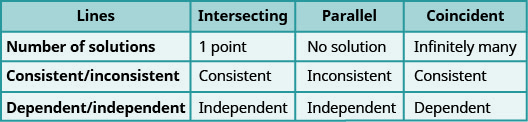
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات:\(\begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases}\)
- إجابة
-
\(\begin{array}{lrrl} \text{We will compare the slopes and intercepts} & \begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases} \\ \text{of the two lines.} \\ \text{The first equation is already in} \\ \text{slope-intercept form.} \\ & {y = 3x - 1}\\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ & 6x-2y &=&12 \\ & -2y &=& -6x - 12 \\ &\frac{-2y}{-2} &=& \frac{-6x + 12}{-2}\\ &y&=&3x-6\\\\ \text{Find the slope and intercept of each line.} & y = 3x-1 & y=3x-6 \\ &m = 3 & m = 3 \\&b=-1 &b=-6 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)
لا يوجد حل لنظام المعادلات الذي تكون رسوماته البيانية عبارة عن خطوط متوازية وهو غير متسق ومستقل.
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
\(\begin{cases}{y=−2x−4} \\ {4x+2y=9}\end{cases}\)
- إجابة
-
لا يوجد حل، غير متناسق، مستقل
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
\(\begin{cases}{y=\frac{1}{3}x−5} \\ {x-3y=6}\end{cases}\)
- إجابة
-
لا يوجد حل، غير متناسق، مستقل
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات:\(\begin{cases}{2x+y=−3} \\ {x−5y=5}\end{cases}\)
- إجابة
-
\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts} & \begin{cases}{2x+y=-3} \\ {x−5y=5}\end{cases} \\ \text{of the two lines.} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &2x+y&=&-3 & x−5y&=&5\\ & y &=& -2x -3 & -5y &=&-x+5 \\ &&&&\frac{-5y}{-5} &=& \frac{-x + 5}{-5}\\ &&&&y&=&\frac{1}{5}x-1\\\\ \text{Find the slope and intercept of each line.} & y &=& -2x-3 & y&=&\frac{1}{5}x-1 \\ &m &=& -2 & m &=& \frac{1}{5} \\&b&=&-3 &b&=&-1 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)
يحتوي نظام المعادلات التي تتقاطع رسوماتها البيانية على حل واحد وهو ثابت ومستقل.
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
\(\begin{cases}{3x+2y=2} \\ {2x+y=1}\end{cases}\)
- إجابة
-
حل واحد، متسق ومستقل
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
\(\begin{cases}{x+4y=12} \\ {−x+y=3}\end{cases}\)
- إجابة
-
حل واحد، متسق ومستقل
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات. \(\begin{cases}{3x−2y=4} \\ {y=\frac{3}{2}x−2}\end{cases}\)
- إجابة
-
\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts of the two lines.}& \begin{cases}{3x−2y} &=&{4} \\ {y}&=&{\frac{3}{2}x−2}\end{cases} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &3x-2y&=&4 \\ & -2y &=& -3x +4 \\ &\frac{-2y}{-2} &=& \frac{-3x + 4}{-2}\\ &y&=&\frac{3}{2}x-2\\\\ \text{Find the slope and intercept of each line.} &y&=&\frac{3}{2}x-2\\ \text{Since the equations are the same, they have the same slope} \\ \text{and samey-intercept and so the lines are coincident.}\end{array}\)
يحتوي نظام المعادلات الذي تكون رسوماته البيانية خطوطًا متزامنة على العديد من الحلول وهو متسق ومعتمد.
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
\(\begin{cases}{4x−5y=20} \\ {y=\frac{4}{5}x−4}\end{cases}\)
- إجابة
-
العديد من الحلول المتسقة والمعتمدة
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
\(\begin{cases}{ −2x−4y=8} \\ {y=−\frac{1}{2}x−2}\end{cases}\)
- إجابة
-
العديد من الحلول المتسقة والمعتمدة
حل تطبيقات أنظمة المعادلات عن طريق التمثيل البياني
سنستخدم نفس استراتيجية حل المشكلات التي استخدمناها في نماذج الرياضيات لإعداد وحل تطبيقات أنظمة المعادلات الخطية. سنقوم بتعديل الإستراتيجية قليلاً هنا لجعلها مناسبة لأنظمة المعادلات.
- اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
- حدد ما نبحث عنه.
- اذكر ما نبحث عنه. اختر المتغيرات لتمثيل تلك الكميات.
- ترجم إلى نظام من المعادلات.
- حل نظام المعادلات باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
الخطوة 5 هي المكان الذي سنستخدم فيه الطريقة المقدمة في هذا القسم. سنرسم المعادلات ونجد الحل.
تقوم شركة Sondra بصنع 10 لترات من عصير الفاكهة والصودا. يبلغ عدد كوارتات عصير الفاكهة 4 أضعاف عدد كوارتات الصودا الغازية. كم كوارتات من عصير الفاكهة وكم كوارتات من الصودا الغازية التي تحتاجها سوندرا؟
- إجابة
-
الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما نبحث عنه.
نحن نبحث عن عدد كوارتات عصير الفاكهة وعدد كوارتات الصودا التي ستحتاجها سوندرا.
الخطوة 3. اذكر ما نبحث عنه. اختر المتغيرات لتمثيل تلك الكميات.
Let f = عدد كوارتات عصير الفاكهة.
c = عدد كوارتات الصودا الغازيةالخطوة 4. ترجم إلى نظام من المعادلات.
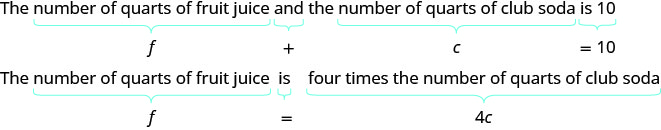
لدينا الآن النظام. \(\begin{cases}{ f+c=10} \\ {f=4c}\end{cases}\)
الخطوة 5. حل نظام المعادلات باستخدام تقنيات الجبر الجيدة.
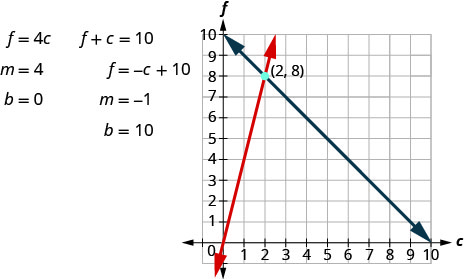
نقطة التقاطع (2، 8) هي الحل. هذا يعني أن Sondra تحتاج إلى 2 كوارت من الصودا الغازية و 8 لترات من عصير الفاكهة.
الخطوة 6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
هل هذا منطقي في المشكلة؟
نعم، عدد كوارتات عصير الفاكهة، 8 يساوي 4 أضعاف عدد كوارتات الصودا، 2.
نعم، 10 كوارت من البانش تساوي 8 كوترات من عصير الفاكهة بالإضافة إلى 2 كوارت من الصودا.
الخطوة 7. أجب على السؤال بجملة كاملة.
تحتاج سوندرا إلى 8 كوارت من عصير الفاكهة و 2 كوارت من الصودا.
يصنع ماني 12 كوارت من عصير البرتقال من المركز والماء. يبلغ عدد كوارتات الماء 3 أضعاف عدد كوارتات التركيز. كم كوارتات من التركيز وكم كوترات من الماء يحتاجها ماني؟
- إجابة
-
يحتاج ماني إلى 3 كوترات من العصير المركز و 9 كوارت من الماء.
تقوم Alisha بإعداد مشروب قهوة بحجم 18 أونصة مصنوع من القهوة المخمرة والحليب. عدد أونصات القهوة المخمرة أكبر بخمس مرات من عدد أونصات الحليب. كم أوقية من القهوة وكم أوقية من الحليب تحتاجها أليشا؟
- إجابة
-
تحتاج أليشا إلى 15 أوقية من القهوة و 3 أونصات من الحليب.
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل أنظمة المعادلات عن طريق الرسوم البيانية.
المفاهيم الرئيسية
- حل نظام المعادلات الخطية بالرسم البياني
- ارسم المعادلة الأولى بيانيًا.
- ارسم المعادلة الثانية على نفس نظام الإحداثيات المستطيلة.
- حدد ما إذا كانت الخطوط تتقاطع أو متوازية أو هي نفس الخط.
- حدد الحل للنظام.
في حالة تقاطع الخطوط، حدد نقطة التقاطع. تحقق للتأكد من أنه حل لكلتا المعادلتين. هذا هو الحل للنظام.
إذا كانت الخطوط متوازية، فلن يكون لدى النظام أي حل.
إذا كانت الخطوط هي نفسها، فإن النظام يحتوي على عدد لا نهائي من الحلول. - تحقق من الحل في كلتا المعادلتين.
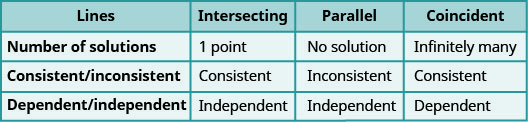
- حدد عدد الحلول من الرسم البياني لنظام خطي
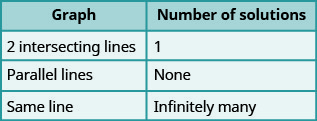
- حدد عدد حلول النظام الخطي من خلال النظر إلى المنحدرات والاعتراضات
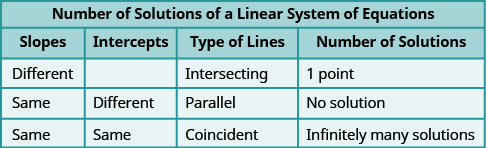
- حدد عدد الحلول وكيفية تصنيف نظام المعادلات
- إستراتيجية حل المشكلات لأنظمة المعادلات الخطية
- اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
- حدد ما نبحث عنه.
- اذكر ما نبحث عنه. اختر المتغيرات لتمثيل تلك الكميات.
- ترجم إلى نظام من المعادلات.
- حل نظام المعادلات باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
مسرد المصطلحات
- خطوط متزامنة
- الخطوط المتزامنة هي الخطوط التي لها نفس المنحدر ونفس التقاطع y.
- نظام ثابت
- نظام المعادلات المتسق هو نظام معادلات بحل واحد على الأقل.
- معادلات تابعة
- تعتمد معادلتان إذا كانت جميع حلول المعادلة الواحدة هي أيضًا حلول للمعادلة الأخرى.
- نظام غير متناسق
- نظام المعادلات غير المتسق هو نظام معادلات بدون حل.
- معادلات مستقلة
- هناك معادلتان مستقلتان إذا كانت لهما حلول مختلفة.
- حلول نظام المعادلات
- حلول نظام المعادلات هي قيم المتغيرات التي تجعل جميع المعادلات صحيحة. يتم تمثيل حل نظام من معادلتين خطيتين بزوج مرتب (x، y).
- نظام المعادلات الخطية
- عندما يتم تجميع معادلتين خطيتين أو أكثر معًا، فإنها تشكل نظامًا من المعادلات الخطية.


