2.6: حل صيغة لمتغير معين
- Page ID
- 200229
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم صيغة المسافة والمعدل والوقت
- حل صيغة لمتغير معين
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- حل:\(15t=120\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.2.1. - حل:\(6x+24=96\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.3.1.
استخدم صيغة المسافة والمعدل والوقت
إحدى الصيغ التي ستستخدمها كثيرًا في الجبر وفي الحياة اليومية هي صيغة المسافة التي يقطعها جسم يتحرك بمعدل ثابت. المعدل هو كلمة مكافئة لـ «السرعة». قد تكون الفكرة الأساسية للسعر مألوفة لك بالفعل. هل تعرف المسافة التي تقطعها إذا كنت تقود السيارة بمعدل ثابت يبلغ 60 ميلاً في الساعة لمدة ساعتين؟ (قد يحدث هذا إذا كنت تستخدم نظام تثبيت السرعة في سيارتك أثناء القيادة على الطريق السريع.) إذا قلت 120 ميلاً، فأنت تعرف بالفعل كيفية استخدام هذه الصيغة!
بالنسبة لجسم يتحرك بمعدل منتظم (ثابت)، ترتبط المسافة المقطوعة والوقت المنقضي والمعدل بالصيغة التالية:
\[\begin{array} {lllll}{ d = r t} &{\text { where }} &{ d} &{=} &{\text{distance}} \\ {} &{} &{ r} &{=} &{\text{rate}} \\{} &{} &{ t} &{=} &{\text{time}} \end{array}\]
سنستخدم استراتيجية حل التطبيقات التي استخدمناها سابقًا في هذا الفصل. عندما تتطلب مشكلتنا صيغة، نقوم بتغيير الخطوة 4. بدلاً من كتابة الجملة، نكتب الصيغة المناسبة. نكتب الخطوات المنقحة هنا كمرجع.
- اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
- حدد ما نبحث عنه.
- اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
- ترجم إلى معادلة. اكتب الصيغة المناسبة للموقف. استبدل المعلومات المعطاة.
- حل المعادلة باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
قد ترغب في إنشاء مخطط صغير لتلخيص المعلومات في المشكلة. انظر المخطط في هذا المثال الأول.
يركب جمال دراجته بمعدل موحد يبلغ 12 ميلاً في الساعة\(3\frac{1}{2}\) لساعات. ما المسافة التي قطعها؟
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما تبحث عنه. المسافة المقطوعة الخطوة 3. اسم. اختر متغيرًا لتمثيله. دعونا د = المسافة. الخطوة 4. ترجمة: اكتب الصيغة المناسبة. \(d=rt\) 
استبدل المعلومات المعطاة. \(d = 12\cdot 3\frac{1}{2}\) الخطوة 5. حل المعادلة. \(d=42\text{ miles}\) الخطوة 6. تحقق هل 42 ميلاً منطقية؟ جمال رايدس: 
الخطوة 7. أجب على السؤال بجملة كاملة. ركب جمال 42 ميلاً.
قاد Lindsay\(5\frac{1}{2}\) لساعات بسرعة 60 ميل في الساعة. ما مقدار المسافة التي قطعتها؟
- إجابة
-
330 ميلاً
مشى ترينه\(2\frac{1}{3}\) لساعات بمعدل 3 أميال في الساعة. إلى أي مدى مشيت؟
- إجابة
-
7 أميال
يخطط ري للقيادة من منزله في سان دييغو لزيارة جدته في ساكرامنتو، على مسافة 520 ميلاً. إذا كان بإمكانه القيادة بمعدل ثابت يبلغ 65 ميلاً في الساعة، فما عدد الساعات التي ستستغرقها الرحلة؟
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما تبحث عنه. كم ساعة (الوقت) الخطوة 3. اسم.
اختر متغيرًا لتمثيله.دعها = الوقت. 
الخطوة 4. ترجم.
اكتب الصيغة المناسبة.\(d=rt\) استبدل المعلومات المعطاة. \(520 = 65t\) الخطوة 5. حل المعادلة. \(t = 8\) الخطوة 6. تحقق. استبدل الأرقام في
الصيغة وتأكد من أن النتيجة عبارة
صحيحة.\(\begin{array}{lll} {d} &{=} &{rt} \\ {520} &{\stackrel{?}{=}} &{65\cdot 8}\\ {520} &{=} &{520\checkmark} \end{array}\) الخطوة 7. أجب على السؤال بجملة كاملة. تستغرق رحلة ري 8 ساعات.
يريد لي أن يقود سيارته من فينيكس إلى شقة أخيه في سان فرانسيسكو، على مسافة 770 ميلاً. إذا كان يقود السيارة بمعدل ثابت يبلغ 70 ميلاً في الساعة، فما عدد الساعات التي ستستغرقها الرحلة؟
- إجابة
-
11 ساعة
تقع Yesenia على بعد 168 ميلاً من شيكاغو. إذا كانت بحاجة إلى أن تكون في شيكاغو في 3 ساعات، فما المعدل الذي تحتاجه للقيادة؟
- إجابة
-
56 ميلا في الساعة
حل صيغة لمتغير معين
ربما تكون على دراية ببعض الصيغ الهندسية. الصيغة هي وصف رياضي للعلاقة بين المتغيرات. تستخدم الصيغ أيضًا في العلوم، مثل الكيمياء والفيزياء والبيولوجيا. في الطب، يتم استخدامها لحسابات صرف الأدوية أو تحديد مؤشر كتلة الجسم. تعتمد برامج جداول البيانات على الصيغ لإجراء العمليات الحسابية. من المهم أن تكون على دراية بالصيغ وأن تكون قادرًا على التلاعب بها بسهولة.
في التمرين\(\PageIndex{1}\) والتمرين\(\PageIndex{4}\)، استخدمنا الصيغة\(d=rt\). تعطي هذه الصيغة قيمة d والمسافة عند استبدال قيم r و t والمعدل والوقت. ولكن في التمرين\(\PageIndex{4}\)، كان علينا إيجاد قيمة t. استبدلنا قيم d و r ثم استخدمنا الجبر لحل tt. إذا كان عليك القيام بذلك كثيرًا، فقد تتساءل عن سبب عدم وجود صيغة تعطي قيمة t عندما تستبدل قيم d و r. يمكننا عمل صيغة كهذه عن طريق حل صيغة\(d=rt\) t.
حل صيغة لمتغير معين يعني عزل هذا المتغير على أحد جانبي علامة التساوي بمعامل 1. جميع المتغيرات والثوابت الأخرى موجودة على الجانب الآخر من علامة التساوي. لمعرفة كيفية حل صيغة لمتغير معين، سنبدأ بصيغة المسافة والمعدل والوقت.
حل الصيغة d=rt لـ t:
- عندما d=520 و r=65
- بشكل عام
- إجابة
-
سنكتب الحلول جنبًا إلى جنب لإثبات أن حل الصيغة بشكل عام يستخدم نفس الخطوات عندما يكون لدينا أرقام لاستبدالها.
1. عندما d=520 و r=65 2. بشكل عام اكتب الصيغة. \(d=rt\) اكتب الصيغة. \(d=rt\) بديل. \(520=65t\) قسّم، لعزله. \(\frac{520}{65} = \frac{65t}{65}\) قسّم، لعزله. \(\frac{d}{r} = \frac{rt}{t}\) قم بالتبسيط. \(8 = t\) قم بالتبسيط. \(\frac{d}{r}=t\) نقول أن الصيغة قد\(t = \frac{d}{r}\) تم حلها من أجل t.
حل الصيغة\(d=rt\) لـ r:
- عندما d=180 و t=4
- بشكل عام
- إجابة
-
- \(r = 45\)
- \(r = \frac{d}{t}\)
حل الصيغة\(d=rt\) لـ r:
- عندما d=780 و t=12
- بشكل عام
- إجابة
-
- \(r = 65\)
- \(r = \frac{d}{rt\)
حل الصيغة\(A = \frac{1}{2}bh\) لـ h:
- متى\(A = 90\) و\(b = 15\)
- بشكل عام
- إجابة
-
يمكننا الآن إيجاد ارتفاع المثلث، إذا عرفنا المساحة والقاعدة، باستخدام الصيغة\(h = \frac{2A}{b}\)1. متى\(A = 90\) و\(b = 15\) 2. بشكل عام اكتب الصيغة. 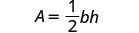
اكتب الصيغة. 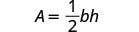
بديل. 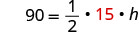
امسح الكسور. 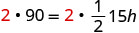
امسح الكسور. 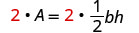
قم بالتبسيط. 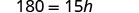
قم بالتبسيط. 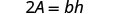
حل لـ h. 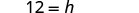
حل لـ hh. 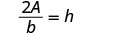
حل الصيغة\(A = \frac{1}{2}bh\) لـ h:
- متى\(A = 170\) و\(b = 17\)
- بشكل عام
- إجابة
-
- \(h = 20\)
- \(h = \frac{2A}{b}\)
حل الصيغة\(A = \frac{1}{2}bh\) لـ h:
- متى\(A = 62\) و\(h = 31\)
- بشكل عام
- إجابة
-
- \(b = 4\)
- \(b = \frac{2A}{h}\)
\(I=Prt\)يتم استخدام الصيغة لحساب الفائدة البسيطة، I، لرأس المال، P، المستثمر بسعر الفائدة، r، لمدة t سنوات.
حل الصيغة I=Prt للعثور على المبدأ، P:
- عندما أكون = 5600 دولار، r = 4%، t = 7 سنوات
- بشكل عام
- إجابة
-
1. I = 5,600 دولار، r = 4%، t = 7 سنوات 2. بشكل عام اكتب الصيغة. 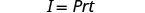
اكتب الصيغة. 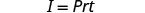
بديل. 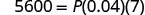
قم بالتبسيط. 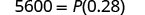
قم بالتبسيط. 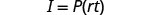
قسّم، لعزل P. 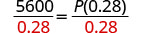
قسّم، لعزل P. 
قم بالتبسيط. 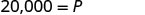
قم بالتبسيط. 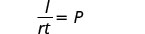
المدير هو 
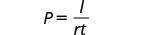
حل الصيغة I=Prt للعثور على المبدأ، P:
- عندما أكون = 2160 دولارًا، r = 6٪، t = 3 سنوات
- بشكل عام
- إجابة
-
- $12000
- \(P = \frac{1}{rt}\)
حل الصيغة I=Prt للعثور على المبدأ، P:
- عندما أكون = 5400 دولار، r= 12٪، t = 5 سنوات
- بشكل عام
- إجابة
-
- 9000 دولار
- \(P = \frac{1}{rt}\)
حل الصيغة 3x+2y=18 لـ y:
- عندما x = 4
- بشكل عام
- إجابة
-
1. عندما x = 4 2. بشكل عام 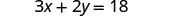
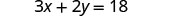
بديل. 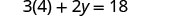
اطرح لعزل
المصطلح y.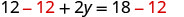
اطرح لعزل
المصطلح y.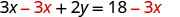
يقسم. 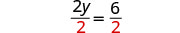
يقسم. 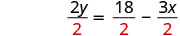
قم بالتبسيط. 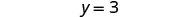
قم بالتبسيط. 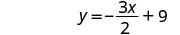
حل الصيغة 3x+4y = 10 لـ y:
- عندما\(x = \frac{14}{3}\)
- بشكل عام
- إجابة
-
- \(y = -1\)
- \(y = \frac{10 - 3x}{4}\)
حل الصيغة 5x+2y=18 لـ y:
- عندما\(x = 4\)
- بشكل عام
- إجابة
-
- \(y = -1\)
- \(y = \frac{18 - 5x}{2}\)
حل الصيغة p=A+B+C لـ a.
- إجابة
-
سنقوم بعزل aa على جانب واحد من المعادلة. 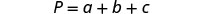
تتم إضافة كل من b و c إلى a، لذلك نطرحهما من كلا طرفي المعادلة. 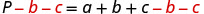
قم بالتبسيط. 
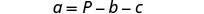
حل الصيغة p=A+B+c لـ b.
- إجابة
-
ب = P−a−c
حل الصيغة p=A+B+C لـ c.
- إجابة
-
C=p−a−b
حل الصيغة 6x+5y=13 لـ y.
- إجابة
-
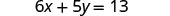
اطرح 6x من كلا الجانبين لعزل المصطلح بـ y. 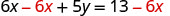
قم بالتبسيط. 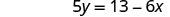
اقسم على 5 لجعل المعامل 1. 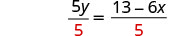
قم بالتبسيط. 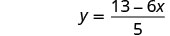
يتم تبسيط الكسر. لا يمكننا تقسيم 13−6x على 5.
حل الصيغة 4x+7y=9 لـ y.
- إجابة
-
\(y = \frac{9 - 4x}{7}\)
حل الصيغة 5x+8y=1 لـ y.
- إجابة
-
\(y = \frac{1 - 5x}{8}\)
المفاهيم الرئيسية
- لحل تطبيق (باستخدام صيغة)
- اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
- حدد ما نبحث عنه.
- اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
- ترجم إلى معادلة. اكتب الصيغة المناسبة للموقف. استبدل المعلومات المعطاة.
- حل المعادلة باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
- المسافة والمعدل والوقت
بالنسبة لجسم يتحرك بمعدل موحد (ثابت)، ترتبط المسافة المقطوعة والوقت المنقضي والمعدل بالصيغة التالية: d=rt حيث d = المسافة، r = المعدل، t = الوقت. - إن حل صيغة لمتغير معين يعني الحصول على هذا المتغير بمفرده بمعامل 1 على أحد طرفي المعادلة وجميع المتغيرات والثوابت الأخرى على الجانب الآخر.


