2.4: استخدم إستراتيجية عامة لحل المعادلات الخطية

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• حل المعادلات باستخدام استراتيجية عامة
• تصنيف المعادلات

ملاحظة

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. قم بالتبسيط:$−(a−4)$.
   إذا فاتتك هذه المشكلة، راجع التمرين 1.10.46
2. الضرب:$\frac{3}{2}(12x+20)$
   إذا فاتتك هذه المشكلة، راجع التمرين 1.10.34.
3. التبسيط:$5−2(n+1)$
   إذا فاتتك هذه المشكلة، راجع التمرين 1.10.49.
4. الضرب:$3(7y+9)$
   إذا فاتتك هذه المشكلة، راجع التمرين 1.10.34.
5. المضاعفة:$(2.5)(6.4)$
   إذا فاتتك هذه المشكلة، راجع التمرين 1.8.19.

حل المعادلات باستخدام الإستراتيجية العامة

لقد تعاملنا حتى الآن مع حل شكل محدد من المعادلة الخطية. لقد حان الوقت الآن لوضع استراتيجية شاملة واحدة يمكن استخدامها لحل أي معادلة خطية. لن تتطلب بعض المعادلات التي نحلها كل هذه الخطوات لحلها، ولكن الكثير منها سيتطلب ذلك.

إن البدء بتبسيط كل جانب من المعادلة يجعل الخطوات المتبقية أسهل.

التمارين الرياضية$\PageIndex{1}$: How to Solve Linear Equations Using the General Strategy

حل:$-6(x + 3) = 24$.

إجابة

التمارين الرياضية$\PageIndex{2}$

حل:$5(x + 3)=35$

إجابة

$x = 4$

التمارين الرياضية$\PageIndex{3}$

حل:$6(y - 4) = -18$

إجابة

$y = 1$

الإستراتيجية العامة لحل المعادلات الخطية.

1. قم بتبسيط كل جانب من المعادلة قدر الإمكان.
   استخدم خاصية التوزيع لإزالة أي أقواس.
   اجمع بين المصطلحات المتشابهة.
2. اجمع كل مصطلحات المتغيرات على جانب واحد من المعادلة.
   استخدم خاصية الجمع أو الطرح للمساواة.
3. اجمع كل المصطلحات الثابتة على الجانب الآخر من المعادلة.
   استخدم خاصية الجمع أو الطرح للمساواة.
4. اجعل معامل المصطلح المتغير يساوي 1.
   استخدم خاصية الضرب أو القسمة للمساواة.
   اذكر حل المعادلة.
5. تحقق من الحل. استبدل الحل بالمعادلة الأصلية للتأكد من أن النتيجة عبارة صحيحة.

التمارين الرياضية$\PageIndex{4}$

حل:$-(y + 9) = 8$

إجابة

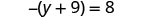
قم بتبسيط كل جانب من المعادلة قدر الإمكان من خلال التوزيع.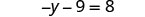
الحد y الوحيد موجود على الجانب الأيسر، لذا فإن جميع مصطلحات المتغيرات موجودة على الجانب الأيسر من المعادلة.
أضف 9 إلى كلا الجانبين للحصول على جميع الشروط الثابتة على الجانب الأيمن من المعادلة.
قم بالتبسيط.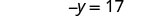
أعد كتابة −y كـ −1y.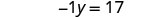
اجعل معامل الحد المتغير يساوي 1 بقسمة كلا الطرفين على −1.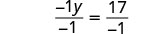
قم بالتبسيط.
تحقق من: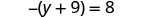
دع y=−17.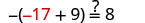

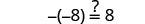
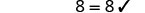
التمارين الرياضية$\PageIndex{5}$

حل:$-(y + 8) = -2$

إجابة

$y = -6$

التمارين الرياضية$\PageIndex{6}$

حل:$-(z + 4) = -12$

إجابة

$z = 8$

التمارين الرياضية$\PageIndex{7}$

حل:$5(a - 3) + 5 = -10$

إجابة

قم بتبسيط كل جانب من المعادلة قدر الإمكان.
توزيع.
اجمع بين المصطلحات المتشابهة.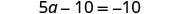
الحد الوحيد موجود على الجانب الأيسر، لذا فإن جميع مصطلحات المتغيرات موجودة على جانب واحد من المعادلة.
أضف 10 إلى كلا الطرفين للحصول على جميع الشروط الثابتة على الجانب الآخر من المعادلة.
قم بالتبسيط.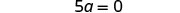
اجعل معامل الحد المتغير يساوي 11 بقسمة كلا الطرفين على 55.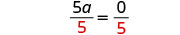
قم بالتبسيط.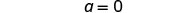
تحقق من: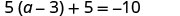
دع = 0.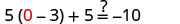

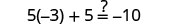
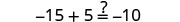
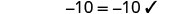
التمارين الرياضية$\PageIndex{8}$

حل:$2(m - 4) + 3 = -1$

إجابة

$m = 2$

التمارين الرياضية$\PageIndex{9}$

حل:$7(n - 3) - 8 = -15$

إجابة

$n = 2$

التمارين الرياضية$\PageIndex{10}$

حل:$\frac{2}{3}(6m - 3) = 8 - m$

إجابة

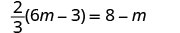
توزيع.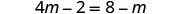
أضف m للحصول على المتغيرات فقط إلى اليسار.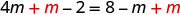
قم بالتبسيط.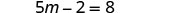
أضف 2 للحصول على الثوابت فقط على اليمين.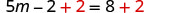
قم بالتبسيط.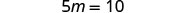
قسّم على 5.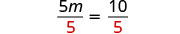
قم بالتبسيط.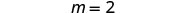
تحقق من: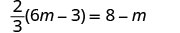
اسمحوا لي = 2.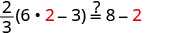

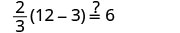
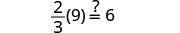
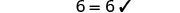
التمارين الرياضية$\PageIndex{11}$

حل:$\frac{1}{3}(6u + 3) = 7 - u$

إجابة

$u = 2$

التمارين الرياضية$\PageIndex{12}$

حل:$\frac{2}{3}(9x - 12) = 8 + 2x$

إجابة

$x = 4$

التمارين الرياضية$\PageIndex{13}$

حل:$8 - 2(3y + 5) = 0$

إجابة

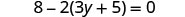
التبسيط - استخدم خاصية التوزيع.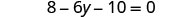
اجمع بين المصطلحات المتشابهة.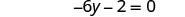
أضف 2 إلى كلا الجانبين لجمع الثوابت على اليمين.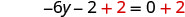
قم بالتبسيط.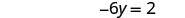
قسّم كلا الجانبين على −6−6.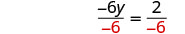
قم بالتبسيط.
تحقق: دع y=−13.

التمارين الرياضية$\PageIndex{14}$

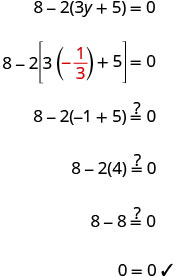
حل:$12 - 3(4j + 3) = -17$

إجابة

$j = \frac{5}{3}$

التمارين الرياضية$\PageIndex{15}$

حل:$-6 - 8(k - 2) = -10$

إجابة

$k = \frac{5}{2}$

التمارين الرياضية$\PageIndex{16}$

حل:$4(x - 1)-2=5(2x+3)+6$

إجابة

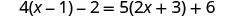
توزيع.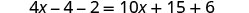
اجمع بين المصطلحات المتشابهة.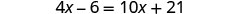
اطرح 4x للحصول على المتغيرات على الجانب الأيمن فقط منذ ذلك الحين$10>4$.
قم بالتبسيط.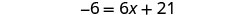
اطرح 21 للحصول على الثوابت على اليسار.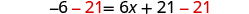
قم بالتبسيط.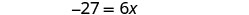
اقسم على 6.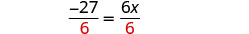
قم بالتبسيط.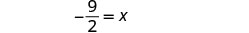
تحقق من:
دعونا$x=-\frac{9}{2}$.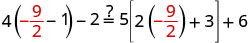

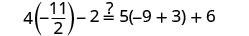
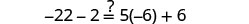
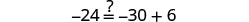
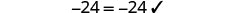
التمارين الرياضية$\PageIndex{17}$

حل:$6(p-3)-7=5(4p+3)-12$

إجابة

$p = -2$

التمارين الرياضية$\PageIndex{18}$

حل:$8(q +1)-5=3(2q-4)-1$

إجابة

$q = -8$

التمارين الرياضية$\PageIndex{19}$

حل:$10[3 - 8(2s-5)] = 15(40 - 5s)$

إجابة

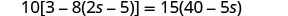
قم بالتبسيط من الأقواس الداخلية أولاً.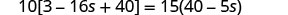
ادمج المصطلحات المتشابهة في الأقواس.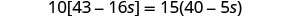
توزيع.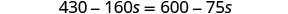
أضف 160 ثانية للحصول على s إلى اليمين.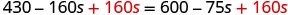
قم بالتبسيط.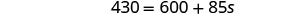
اطرح 600 للحصول على الثوابت على اليسار.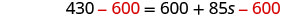
قم بالتبسيط.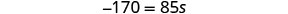
يقسم.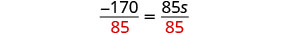
قم بالتبسيط.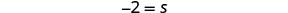
تحقق من: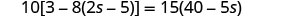
البديل s=−2.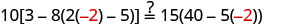

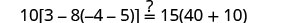
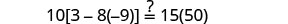
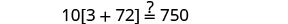
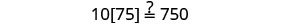
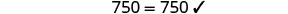
التمارين الرياضية$\PageIndex{20}$

حل:$6[4−2(7y−1)]=8(13−8y)$.

إجابة

$y = -\frac{17}{5}$

التمارين الرياضية$\PageIndex{21}$

حل:$12[1−5(4z−1)]=3(24+11z)$.

إجابة

$z = 0$

التمارين الرياضية$\PageIndex{22}$

حل:$0.36(100n+5)=0.6(30n+15)$.

إجابة

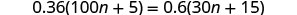
توزيع.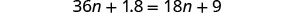
اطرح 18n للحصول على المتغيرات على اليسار.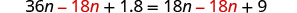
قم بالتبسيط.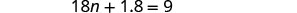
اطرح 1.8 للحصول على الثوابت على اليمين.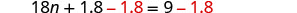
قم بالتبسيط.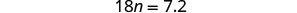
يقسم.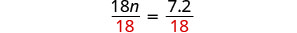
قم بالتبسيط.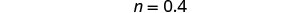
تحقق من: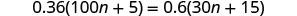
دعونا ن=0.4.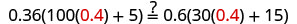

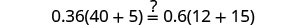
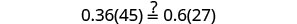
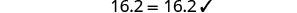
التمارين الرياضية$\PageIndex{23}$

حل:$0.55(100n+8)=0.6(85n+14)$.

إجابة

$n = 1$

التمارين الرياضية$\PageIndex{24}$

حل:$0.15(40m−120)=0.5(60m+12)$.

إجابة

$m = -1$

تصنيف المعادلات

ضع في اعتبارك المعادلة التي حللناها في بداية القسم الأخير، 7x+8=−13. كان الحل الذي وجدناه هو x=−3. وهذا يعني أن المعادلة 7x+8=−13 صحيحة عندما نستبدل المتغير، x، بالقيمة −3. أظهرنا ذلك عندما فحصنا الحل x=−3 وقيّمنا 7x+8=−13 لـ x=−3.

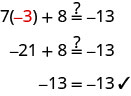
إذا قمنا بتقييم 7x+8 لقيمة مختلفة لـ x، فلن يكون الجانب الأيسر −13.

تكون المعادلة 7x+8=−13 صحيحة عندما نستبدل المتغير، x، بالقيمة −3، ولكن ليس صحيحًا عندما نستبدل x بأي قيمة أخرى. يعتمد ما إذا كانت المعادلة 7x+8=−13 صحيحة أم لا على قيمة المتغير. تسمى المعادلات مثل هذه المعادلات الشرطية.

جميع المعادلات التي قمنا بحلها حتى الآن هي معادلات شرطية.

معادلة شرطية

المعادلة الصحيحة لقيمة واحدة أو أكثر من قيم المتغير والخاطئة لجميع القيم الأخرى للمتغير هي معادلة شرطية.

الآن دعونا ننظر في المعادلة 2y+6=2 (y+3). هل تدرك أن الجانب الأيسر والجانب الأيمن متساويان؟ دعونا نرى ما يحدث عندما نحلها لـ y.

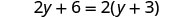قم بالتوزيع.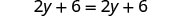
اطرح 2y للحصول على الحرف y على جانب واحد.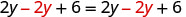
التبسيط - لقد ولت الأشياء!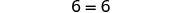

لكن 6=6 صحيح.

هذا يعني أن المعادلة 2y+6=2 (y+3) صحيحة لأي قيمة y. نقول أن حل المعادلة هو جميع الأرقام الحقيقية. المعادلة التي تنطبق على أي قيمة للمتغير مثل هذا تسمى الهوية.

الهوية

المعادلة التي تنطبق على أي قيمة للمتغير تسمى الهوية.

حل الهوية هو كل الأرقام الحقيقية.

ماذا يحدث عندما نحل المعادلة 5z=5z−1؟

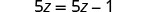اطرح 5z للحصول على الثابت وحده على اليمين.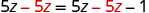
البساطة - اختفت الألف!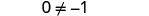

لكن$0\neq −1$.

حل المعادلة 5z=5z−1 أدى إلى العبارة الخاطئة 0=−1. لن تكون المعادلة 5z=5z−1 صحيحة بالنسبة لأي قيمة من z، فهي لا تحتوي على حل. تسمى المعادلة التي لا تحتوي على حل، أو التي تكون خاطئة لجميع قيم المتغير، بالتناقض.

تناقض

تسمى المعادلة الخاطئة لجميع قيم المتغير بالتناقض.

التناقض ليس له حل.

التمارين الرياضية$\PageIndex{25}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض. ثم اذكر الحل.

$6(2n−1)+3=2n−8+5(2n+1)$

إجابة

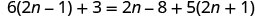
قم بالتوزيع.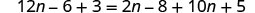
اجمع بين المصطلحات المتشابهة.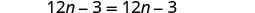
اطرح 12n للحصول على nn على جانب واحد.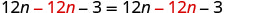
قم بالتبسيط.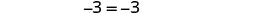
هذا بيان حقيقي.	المعادلة هي هوية. الحل هو جميع الأرقام الحقيقية.

التمارين الرياضية$\PageIndex{26}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:

$4+9(3x−7)=−42x−13+23(3x−2)$

إجابة

الهوية؛ جميع الأرقام الحقيقية

التمارين الرياضية$\PageIndex{27}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:

$8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1$

إجابة

الهوية؛ جميع الأرقام الحقيقية

التمارين الرياضية$\PageIndex{28}$

صنّف كمعادلة شرطية أو هوية أو تناقض. ثم اذكر الحل.

$10+4(p−5)=0$

إجابة

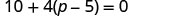
قم بالتوزيع.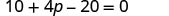
اجمع بين المصطلحات المتشابهة.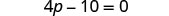
أضف 10 إلى كلا الجانبين.
قم بالتبسيط.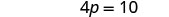
يقسم.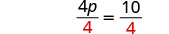
قم بالتبسيط.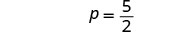
تكون المعادلة صحيحة عندما$p = frac{5}{2}$.	هذه معادلة شرطية. الحل هو$p = frac{5}{2}$.

التمارين الرياضية$\PageIndex{29}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:$11(q+3)−5=19$

إجابة

معادلة شرطية؛\ (q =\ frac {9} {11}\

التمارين الرياضية$\PageIndex{30}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:$6+14(k−8)=95$

إجابة

معادلة شرطية؛$k = \frac{193}{14}$

التمارين الرياضية$\PageIndex{31}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض. ثم اذكر الحل.

$5m+3(9+3m)=2(7m−11)$

إجابة

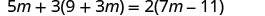
قم بالتوزيع.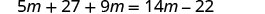
اجمع بين المصطلحات المتشابهة.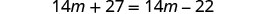
اطرح 14 م من كلا الجانبين.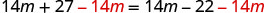
قم بالتبسيط.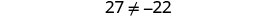
لكن$27\neq −22$.	المعادلة عبارة عن تناقض. ليس لديها حل.

التمارين الرياضية$\PageIndex{32}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:

$12c+5(5+3c)=3(9c−4)$

إجابة

تناقض؛ لا يوجد حل

التمارين$\PageIndex{33}$

صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:

$4(7d+18)=13(3d−2)−11d$

إجابة

تناقض؛ لا يوجد حل

نوع المعادلة	ماذا يحدث عند حلها؟	الحل
معادلة شرطية	صحيح لقيمة واحدة أو أكثر من المتغيرات وخطأ لجميع القيم الأخرى	قيمة واحدة أو أكثر
الهوية	صحيح لأي قيمة للمتغير	جميع الأرقام الحقيقية
التناقض	خطأ لجميع قيم المتغير	لا يوجد حل

المفاهيم الرئيسية

• الإستراتيجية العامة لحل المعادلات الخطية
  1. قم بتبسيط كل جانب من المعادلة قدر الإمكان.
     استخدم خاصية التوزيع لإزالة أي أقواس.
     اجمع بين المصطلحات المتشابهة.
  2. اجمع كل مصطلحات المتغيرات على جانب واحد من المعادلة.
     استخدم خاصية الجمع أو الطرح للمساواة.
  3. اجمع كل المصطلحات الثابتة على الجانب الآخر من المعادلة.
     استخدم خاصية الجمع أو الطرح للمساواة.
  4. اجعل معامل المصطلح المتغير يساوي 1.
     استخدم خاصية الضرب أو القسمة للمساواة.
     اذكر حل المعادلة.
  5. تحقق من الحل.
     استبدل الحل بالمعادلة الأصلية.