الفصل 1 تمارين المراجعة
- Page ID
- 200622
تمارين مراجعة الفصل
مقدمة عن الأعداد الصحيحة
استخدم القيمة المكانية مع الرقم الصحيح
في التمارين التالية، ابحث عن القيمة المكانية لكل رقم.
26,915
- 1
- 2
- 9
- 5
- 6
- إجابة
-
- عشرات
- عشرة آلاف
- مئات
- منها
- الآلاف
359,417
- 9
- 3
- 4
- 7
- 1
58,129,304
- 5
- 0
- 1
- 8
- 2
- إجابة
-
- عشرة ملايين
- عشرات
- مئات الآلاف
- ملايين
- عشرة آلاف
9,430,286,157
- 6
- 4
- 9
- 0
- 5
في التمارين التالية، قم بتسمية كل رقم.
6,104
- إجابة
-
ستة آلاف ومائة وأربعة
493,068
3,975,284
- إجابة
-
ثلاثة ملايين، تسعمائة وخمسة وسبعون ألفاً، مائتان وأربعة وثمانون
85,620,435
في التمارين التالية، اكتب كل رقم كرقم صحيح باستخدام الأرقام.
ثلاثمائة وخمسة عشر
- إجابة
-
315
خمسة وستون ألفا وتسعمائة واثني عشر
تسعون مليون، أربعمائة وخمسة وعشرون ألفا، ستة عشر
- إجابة
-
90,425,016
مليار، ثلاثة وأربعون مليونًا، تسعمائة واثنان وعشرون ألفًا، ثلاثمائة وأحد عشر
في التمارين التالية، قم بالتقريب إلى القيمة المكانية المشار إليها.
قرِّب إلى أقرب عشرة.
- 407
- 8,564
- إجابة
-
- 410
- 8,560
قرِّب إلى أقرب مائة.
- 25,846
- 25,864
في التمارين التالية، قم بتقريب كل رقم إلى أقرب 1. مائة و 2 ألف و 3. عشرة آلاف.
864,951
- إجابة
-
- 865,000,865,000
- 865,000,865,000
- 860,000
3,972,849
تحديد المضاعفات والعوامل
في التمارين التالية، استخدم اختبارات القسمة لتحديد ما إذا كان كل رقم قابلاً للقسمة على 2، وعلى 3، وعلى 5، وعلى 6، وعلى 10.
168
- إجابة
-
بواسطة 2,3,6
264
375
- إجابة
-
بواسطة 3,5
750
1430
- إجابة
-
بحلول 2,5,10
1080
ابحث عن العوامل الأولية والمضاعفات الشائعة الأقل
في التمارين التالية، ابحث عن التحليل الأولي.
420
- إجابة
-
2\(\cdot 2 \cdot 3 \cdot 5 \cdot 7\)
115
225
- إجابة
-
3\(\cdot 3 \cdot 5 \cdot 5\)
2475
1560
- إجابة
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13\)
56
72
- إجابة
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\)
168
252
- إجابة
-
\(2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)
391
في التمارين التالية، ابحث عن المضاعف المشترك الأصغر للأرقام التالية باستخدام طريقة المضاعفات.
6,15
- إجابة
-
30
60، 75
في التمارين التالية، ابحث عن المضاعف المشترك الأصغر للأرقام التالية باستخدام طريقة العوامل الأولية.
24، 30
- إجابة
-
120
70، 84
استخدم لغة الجبر
استخدم المتغيرات والرموز الجبرية
في التمارين التالية، ترجم ما يلي من الجبر إلى اللغة الإنجليزية.
25-7
- إجابة
-
25 ناقص 7، الفرق بين خمسة وعشرين وسبعة
5\(\cdot 6\)
\(45 \div 5\)
- إجابة
-
45 مقسومًا على 5، حاصل القسمة خمسة وأربعين وخمسة وأربعين
x+8
\(42 \geq 27\)
- إجابة
-
اثنان وأربعون أكبر من أو يساوي سبعة وعشرين
3n=24
\(3 \leq 20 \div 4\)
- إجابة
-
3 أقل من أو يساوي 20 مقسومًا على 4، وثلاثة أقل من أو يساوي حاصل القسمة عشرين وأربعة
\(a \neq 7 \cdot 4\)
في التمارين التالية، حدد ما إذا كان كل منها تعبيرًا أم معادلة.
\(6 \cdot 3+5\)
- إجابة
-
التعبير
ص−8=32
تبسيط التعبيرات باستخدام ترتيب العمليات
في التمارين التالية، قم بتبسيط كل تعبير.
\(3^{5}\)
- إجابة
-
243
\(10^{8}\)
في التمارين التالية، قم بالتبسيط
6+10/2+2
- إجابة
-
13
9+12/3+4
\(20 \div(4+6) \cdot 5\)
- إجابة
-
10
\(33 \div(3+8) \cdot 2\)
\(4^{2}+5^{2}\)
- إجابة
-
41
\((4+5)^{2}\)
تقييم تعبير
في التمارين التالية، قم بتقييم التعبيرات التالية.
9x+7 عندما x = 3
- إجابة
-
34
5x−4 عندما x = 6
\(x^{4}\)عندما\(x=3\)
- إجابة
-
81
\(3^{x}\)عندما\(x=3\)
\(x^{2}+5 x-8\)عندما\(x=6\)
- إجابة
-
58
\(2 x+4 y-5\)عندما
\(x=7, y=8\)
قم بتبسيط التعبيرات من خلال دمج المصطلحات المتشابهة
في التمارين التالية، حدد معامل كل مصطلح.
12 دقيقة
- إجابة
-
12
9\(x^{2}\)
في التمارين التالية، حدد المصطلحات المتشابهة.
\(3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}\)
- إجابة
-
12\(3, n^{2}\) و 3\(n^{2}\)
\(5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s\)
في التمارين التالية، حدد المصطلحات في كل تعبير.
\(11 x^{2}+3 x+6\)
- إجابة
-
\(11 x^{2}, 3 x, 6\)
\(22 y^{3}+y+15\)
في التمارين التالية، قم بتبسيط التعبيرات التالية من خلال الجمع بين المصطلحات المتشابهة.
17 أ+9 أ
- إجابة
-
26 أ
18z+9z
9x+3x+8
- إجابة
-
12 × +8
8 أ+5 أ+9
7p+6+5p−4
- إجابة
-
12p+2
8x+7+4x−5
ترجمة عبارة إنجليزية إلى تعبير جبري
في التمارين التالية، ترجم العبارات التالية إلى تعبيرات جبرية.
مجموع 8 و 12
- إجابة
-
8+12
مجموع 9 و 1
الفرق بين x و 4
- إجابة
-
x−4
الفرق بين x و 3
منتج من 6 و y
- إجابة
-
6 سنوات
منتج 9 و y
اشترت أديل تنورة وبلوزة. تكلفة التنورة 15 دولارًا أكثر من البلوزة. دع bb تمثل تكلفة البلوزة. اكتب تعبيرًا يُعبِّر عن تكلفة التنورة.
- إجابة
-
ب+15
لدى مارسيلا 6 أبناء عمومة أقل من بنات عمومتها. دعونا نمثل عدد بنات العمومة. اكتب مقدارًا يُعبِّر عن عدد أبناء العمومة من الأولاد.
جمع الأعداد الصحيحة وطرحها
استخدم السلبيات والأضداد للأعداد الصحيحة
في التمارين التالية، قم بترتيب كل زوج من أزواج الأرقام التالية باستخدام < or >.
- 6___2
- −7___4
- −9___−1
- 9___−3
- إجابة
-
- >
- <
- <
- >
- −5___1
- −4___−9
- 6___10
- 3___−8
في التمارين التالية، ابحث عن عكس كل رقم.
- −8
- 1
- إجابة
-
- 8
- −1
- −2
- 6
في التمارين التالية، قم بالتبسيط.
− (−19)
- إجابة
-
19
− (−53)
في التمارين التالية، قم بالتبسيط.
−م عندما
- م = 3
- m=−3
- إجابة
-
- −3
- 3
−p عندما
- p=6
- p=−6
قم بتبسيط التعبيرات ذات القيمة المطلقة
في التمارين التالية، قم بالتبسيط.
- |7|
- |−25|
- |0|
- إجابة
-
- 7
- 25
- 0
- |5|
- |0|
- |−19|
في التمارين التالية، املأ < أو > أو = لكل زوج من أزواج الأرقام التالية.
- −8___|−8|
- −|−2|___−2
- إجابة
-
- <
- =
- |−3|___−|−3|
- 4___−|−4|
في التمارين التالية، قم بالتبسيط.
|8-4|
- إجابة
-
4
|9-6|
8 (14-2|−2|)
- إجابة
-
80
6 (13-4|−2|)
في التمارين التالية، قم بالتقييم.
1. |x| عندما x=−28
- إجابة
-
- 28
- 15
- yعندما y=−37
- |−z| عندما z=−24
إضافة أعداد صحيحة
في التمارين التالية، قم بتبسيط كل تعبير.
−200+65
- إجابة
-
−135
−150+45
2+ (−8) +6
- إجابة
-
0
4+ (−9) +7
140+ (−75) +67
- إجابة
-
132
−32+24+ (−6) +10
طرح الأعداد الصحيحة
في التمارين التالية، قم بالتبسيط.
9-3
- إجابة
-
6
−5− (−1)
- 15-6
- 15+ (−6)
- إجابة
-
- 9
- 9
- 12-9
- 12+ (−9)
- 8− (−9)
- 8+9
- إجابة
-
- 17
- 17
- 4− (−4)
- 4+4
في التمارين التالية، قم بتبسيط كل تعبير.
10− (−19)
- إجابة
-
29
1− (−18)
31-79
- إجابة
-
−48
39-81
−31-11
- إجابة
-
−42
−32-18
−15− (−28) +5
- إجابة
-
18
71+ (−10) −8
−16− (−4+1) −7
- إجابة
-
-20
−15− (−6+4) −3
ضرب الأعداد الصحيحة
في التمارين التالية، اضرب.
−5 (7)
- إجابة
-
−35
−8 (6)
−18 (−2)
- إجابة
-
36
−10 (−6)
تقسيم الأعداد الصحيحة
في التمارين التالية، قسّم.
\(-28 \div 7\)
- إجابة
-
-4
\(56 \div(-7)\)
\(-120 \div(-20)\)
- إجابة
-
6
\(-200 \div 25\)
تبسيط التعبيرات باستخدام الأعداد الصحيحة
في التمارين التالية، قم بتبسيط كل تعبير.
−8 (−2) −3 (−9)
- إجابة
-
43
−7 (−4) −5 (−3)
\((-5)^{3}\)
- إجابة
-
−125
\((-4)^{3}\)
\(-4 \cdot 2 \cdot 11\)
- إجابة
-
−88
\(-5 \cdot 3 \cdot 10\)
\(-10(-4) \div(-8)\)
- إجابة
-
-5
\(-8(-6) \div(-4)\)
31-4 (3−9)
- إجابة
-
55
24-3 (2−10)
إيجاد قيمة التعبيرات المتغيرة باستخدام الأعداد الصحيحة
في التمارين التالية، قم بتقييم كل تعبير.
x+8 متى
- x=−26
- x=−95
- إجابة
-
- −18
- −87
+9 متى
- ص=−29
- ص=−84
عندما b=−11، قم بتقييم:
- ب+6
- −ب+6
- إجابة
-
- −5
- 17
عند c=−9، قم بتقييم:
- ج+ (−4) ج+ (−4)
- −c+ (−4)
\(p^{2}-5 p+2\)عندما
\(p=-1\)
- إجابة
-
8
\(q^{2}-2 q+9\)عندما\(q=-2\)
\(6 x-5 y+15\)متى\(x=3\) و\(y=-1\)
- إجابة
-
38
\(3 p-2 q+9\)متى\(p=8\) و\(q=-2\)
ترجمة العبارات الإنجليزية إلى التعبيرات الجبرية
في التمارين التالية، ترجم إلى تعبير جبري وقم بتبسيطه إن أمكن.
زاد مجموع −4 و−17 بمقدار 32
- إجابة
-
(−4+ (−17)) +32؛ 11
- الفرق بين 15 و −7
- اطرح 15 من −7
حاصل القسمة −45 و−9
- إجابة
-
\(\frac{-45}{-9} ; 5\)
حاصل ضرب −12 والفرق بين c و d
استخدم الأعداد الصحيحة في التطبيقات
في التمارين التالية، قم بحل.
درجة الحرارة كانت درجة الحرارة المرتفعة ذات يوم في ميامي بيتش بولاية فلوريدا 76 درجة. وفي نفس اليوم، كانت درجة الحرارة المرتفعة في بوفالو بنيويورك −8 درجات. ما الفرق بين درجة الحرارة في ميامي بيتش ودرجة الحرارة في بوفالو؟
- إجابة
-
84 درجة
الحساب الجاري: تمتلك أدريان رصيدًا قدره -22 دولارًا في حسابها الجاري. قامت بإيداع 301 دولار في الحساب. ما هو الرصيد الجديد؟
تصوّر الكسور
ابحث عن الكسور المتكافئة
في التمارين التالية، أوجد ثلاثة كسور مكافئة للكسر المعطى. اعرض عملك باستخدام الأشكال أو الجبر.
\(\frac{1}{4}\)
- إجابة
-
\(\frac{2}{8}, \frac{3}{12}, \frac{4}{16}\)قد تختلف الإجابات
\(\frac{1}{3}\)
\(\frac{5}{6}\)
- إجابة
-
\(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}\)قد تختلف الإجابات
\(\frac{2}{7}\)
تبسيط الكسور
في التمارين التالية، قم بالتبسيط.
\(\frac{7}{21}\)
- إجابة
-
\(\frac{1}{3}\)
\(\frac{8}{24}\)
\(\frac{15}{20}\)
- إجابة
-
\(\frac{3}{4}\)
\(\frac{12}{18}\)
\(-\frac{168}{192}\)
- إجابة
-
\(-\frac{7}{8}\)
\(-\frac{140}{224}\)
\(\frac{11 x}{11 y}\)
- إجابة
-
\(\frac{x}{y}\)
\(\frac{15 a}{15 b}\)
ضرب الكسور
في التمارين التالية، اضرب.
\(\frac{2}{5} \cdot \frac{1}{3}\)
- إجابة
-
\(\frac{2}{15}\)
\(\frac{1}{2} \cdot \frac{3}{8}\)
\(\frac{7}{12}\left(-\frac{8}{21}\right)\)
- إجابة
-
\(-\frac{2}{9}\)
\(\frac{5}{12}\left(-\frac{8}{15}\right)\)
\(-28 p\left(-\frac{1}{4}\right)\)
- إجابة
-
7 ص
\(-51 q\left(-\frac{1}{3}\right)\)
\(\frac{14}{5}(-15)\)
- إجابة
-
−42
\(-1\left(-\frac{3}{8}\right)\)
قسمة الكسور
في التمارين التالية، قسّم
\(\frac{1}{2} \div \frac{1}{4}\)
- إجابة
-
2
\(\frac{1}{2} \div \frac{1}{8}\)
\(-\frac{4}{5} \div \frac{4}{7}\)
- إجابة
-
\(-\frac{7}{5}\)
\(-\frac{3}{4} \div \frac{3}{5}\)
\(\frac{5}{8} \div \frac{a}{10}\)
- إجابة
-
\(\frac{25}{4 a}\)
\(\frac{5}{6} \div \frac{c}{15}\)
\(\frac{7 p}{12} \div \frac{21 p}{8}\)
- إجابة
-
\(\frac{2}{9}\)
\(\frac{5 q}{12} \div \frac{15 q}{8}\)
\(\frac{2}{5} \div(-10)\)
- إجابة
-
\(-\frac{1}{25}\)
\(-18 \div-\left(\frac{9}{2}\right)\)
في التمارين التالية، قم بالتبسيط.
\(\frac{\frac{2}{3}}{\frac{8}{9}}\)
- إجابة
-
\(\frac{3}{4}\)
\(\frac{\frac{4}{5}}{\frac{8}{15}}\)
\(\frac{-\frac{9}{10}}{3}\)
- إجابة
-
\(-\frac{3}{10}\)
\(\frac{2}{\frac{5}{8}}\)
\(\frac{\frac{r}{5}}{\frac{s}{3}}\)
- إجابة
-
\(\frac{3 r}{5 s}\)
\(\frac{-\frac{x}{6}}{-\frac{8}{9}}\)
قم بتبسيط التعبيرات المكتوبة باستخدام شريط الكسر
في التمارين التالية، قم بالتبسيط.
\(\frac{4+11}{8}\)
- إجابة
-
\(\frac{15}{8}\)
\(\frac{9+3}{7}\)
\(\frac{30}{7-12}\)
- إجابة
-
-6
\(\frac{15}{4-9}\)
\(\frac{22-14}{19-13}\)
- إجابة
-
\(\frac{4}{3}\)
\(\frac{15+9}{18+12}\)
\(\frac{5 \cdot 8}{-10}\)
- إجابة
-
-4
\(\frac{3 \cdot 4}{-24}\)
\(\frac{15 \cdot 5-5^{2}}{2 \cdot 10}\)
- إجابة
-
\(\frac{5}{2}\)
\(\frac{12 \cdot 9-3^{2}}{3 \cdot 18}\)
\(\frac{2+4(3)}{-3-2^{2}}\)
- إجابة
-
-2
\(\frac{7+3(5)}{-2-3^{2}}\)
ترجمة العبارات إلى التعبيرات ذات الكسور
في التمارين التالية، ترجم كل عبارة إنجليزية إلى تعبير جبري.
حاصل قسمة c ومجموع d و 9.
- إجابة
-
\(\frac{c}{d+9}\)
حاصل قسمة الفرق بين h و k و −5.
جمع الكسور وطرحها
جمع وطرح الكسور ذات المقام المشترك
في التمارين التالية، أضف.
\(\frac{4}{9}+\frac{1}{9}\)
- إجابة
-
\(\frac{5}{9}\)
\(\frac{2}{9}+\frac{5}{9}\)
\(\frac{y}{3}+\frac{2}{3}\)
- إجابة
-
\(\frac{y+2}{3}\)
\(\frac{7}{p}+\frac{9}{p}\)
\(-\frac{1}{8}+\left(-\frac{3}{8}\right)\)
- إجابة
-
\(-\frac{1}{2}\)
\(-\frac{1}{8}+\left(-\frac{5}{8}\right)\)
في التمارين التالية، اطرح.
\(\frac{4}{5}-\frac{1}{5}\)
- إجابة
-
\(\frac{3}{5}\)
\(\frac{4}{5}-\frac{3}{5}\)
\(\frac{y}{17}-\frac{9}{17}\)
- إجابة
-
\(\frac{y-9}{17}\)
\(\frac{x}{19}-\frac{8}{19}\)
\(-\frac{8}{d}-\frac{3}{d}\)
- إجابة
-
\(-\frac{11}{d}\)
\(-\frac{7}{c}-\frac{7}{c}\)
جمع أو طرح الكسور ذات المقامات المختلفة
في التمارين التالية، قم بالجمع أو الطرح.
\(\frac{1}{3}+\frac{1}{5}\)
- إجابة
-
\(\frac{8}{15}\)
\(\frac{1}{4}+\frac{1}{5}\)
\(\frac{1}{5}-\left(-\frac{1}{10}\right)\)
- إجابة
-
\(\frac{3}{10}\)
\(\frac{1}{2}-\left(-\frac{1}{6}\right)\)
\(\frac{2}{3}+\frac{3}{4}\)
- إجابة
-
\(\frac{17}{12}\)
\(\frac{3}{4}+\frac{2}{5}\)
\(\frac{11}{12}-\frac{3}{8}\)
- إجابة
-
\(\frac{13}{24}\)
\(\frac{5}{8}-\frac{7}{12}\)
\(-\frac{9}{16}-\left(-\frac{4}{5}\right)\)
- إجابة
-
\(\frac{19}{80}\)
\(-\frac{7}{20}-\left(-\frac{5}{8}\right)\)
\(1+\frac{5}{6}\)
- إجابة
-
\(\frac{11}{6}\)
\(1-\frac{5}{9}\)
استخدم ترتيب العمليات لتبسيط الكسور المركبة
في التمارين التالية، قم بالتبسيط.
\(\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}\)
- إجابة
-
\(\frac{1}{275}\)
\(\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}\)
\(\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}\)
- إجابة
-
14
\(\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}\)
إيجاد قيمة التعبيرات المتغيرة التي تحتوي على كسور
في التمارين التالية، قم بالتقييم.
\(x+\frac{1}{2}\)عندما
- \(x=-\frac{1}{8}\)
- \(x=-\frac{1}{2}\)
- إجابة
-
- \(\frac{3}{8}\)
- \(0\)
\(x+\frac{2}{3}\)عندما
- \(x=-\frac{1}{6}\)
- \(x=-\frac{5}{3}\)
4\(p^{2} q\) متى\(p=-\frac{1}{2}\) و\(q=\frac{5}{9}\)
- إجابة
-
\(\frac{5}{9}\)
5\(m^{2} n\) متى\(m=-\frac{2}{5}\) و\(n=\frac{1}{3}\)
\(\frac{u+v}{w}\)عندما
\(u=-4, v=-8, w=2\)
- إجابة
-
-6
\(\frac{m+n}{p}\)عندما
\(m=-6, n=-2, p=4\)
الأرقام العشرية
اسم الأعداد العشرية وكتابتها
في التمارين التالية، اكتب على هيئة عدد عشري.
ثمانية وثلاثمائة
- إجابة
-
8.03
تسعة وسبعمائة
واحد من الألف
- إجابة
-
0.001
تسعة آلاف
في التمارين التالية، قم بتسمية كل رقم عشري.
7.8
- إجابة
-
سبعة وثمانية أعشار
5.01
0.005
- إجابة
-
خمسة آلاف
0.381
الأعداد العشرية المستديرة
في التمارين التالية، قم بتقريب كل رقم إلى الأقرب
- جزء من مئة
- العاشر
- رقم صحيح.
5.7932
- إجابة
-
- 5.79
- 5.8
- 6
3.6284
12.4768
- إجابة
-
- 12.48
- 12.5
- 12
25.8449
جمع الأعداد العشرية وطرحها
في التمارين التالية، قم بالجمع أو الطرح.
18.37+9.36
- إجابة
-
27.73
256.37-85.49
15.35-20.88
- إجابة
-
−5.53
37.5 +12.23
−4.2+ (−9.3)
- إجابة
-
−13.5
−8.6+ (−8.6)
100-64.2
- إجابة
-
35.8
100-65.83
2.51+40
- إجابة
-
42.51
9.38+60
ضرب الأعداد العشرية وقسمتها
في التمارين التالية، اضرب.
(0.3) (0.4)
- إجابة
-
0.12
(0.6) (0.7)
(8.52) (3.14)
- إجابة
-
26.7528
(5.32) (4.86)
(0.09) (24.78)
- إجابة
-
2.2302
(0.04) (36.89)
في التمارين التالية، قسّم.
\(0.15 \div 5\)
- إجابة
-
0.03
\(0.27 \div 3\)
\(\$ 8.49 \div 12\)
- إجابة
-
$0.71
\(\$ 16.99 \div 9\)
\(12 \div 0.08\)
- إجابة
-
150
\(5 \div 0.04\)
تحويل الأعداد العشرية والكسور والنسب المئوية
في التمارين التالية، اكتب كل عدد عشري في صورة كسر.
0.08
- إجابة
-
\(\frac{2}{25}\)
0.17
0.425
- إجابة
-
\(\frac{17}{40}\)
0.184
1.75
- إجابة
-
\(\frac{7}{4}\)
0.035
في التمارين التالية، قم بتحويل كل كسر إلى عدد عشري.
\(\frac{2}{5}\)
- إجابة
-
0.4
\(\frac{4}{5}\)
\(-\frac{3}{8}\)
- إجابة
-
−0.375
\(-\frac{5}{8}\)
\(\frac{5}{9}\)
- إجابة
-
\(0 . \overline{5}\)
\(\frac{2}{9}\)
\(\frac{1}{2}+6.5\)
- إجابة
-
7
\(\frac{1}{4}+10.75\)
في التمارين التالية، قم بتحويل كل نسبة مئوية إلى عدد عشري.
5%
- إجابة
-
0.05
9%
40%
- إجابة
-
0.4
50%
115%
- إجابة
-
1.15
125%
في التمارين التالية، قم بتحويل كل عدد عشري إلى نسبة مئوية.
0.18
- إجابة
-
18%
0.15
0.009
- إجابة
-
0.9%
0.008
1.5
- إجابة
-
150%
2.2
الأرقام الحقيقية
تبسيط التعبيرات باستخدام الجذور التربيعية
في التمارين التالية، قم بالتبسيط.
\(\sqrt{64}\)
- إجابة
-
8
\(\sqrt{144}\)
\(-\sqrt{25}\)
- إجابة
-
-5
\(-\sqrt{81}\)
تحديد الأعداد الصحيحة والأعداد النسبية والأعداد غير النسبية والأعداد الحقيقية
في التمارين التالية، اكتب كنسبة عددين صحيحين.
- 9
- 8.47
- إجابة
-
- \(\frac{9}{1}\)
- \(\frac{847}{100}\)
- −15
- 3.591
في التمارين التالية، قم بإدراج
- أرقام عقلانية،
- أرقام غير منطقية.
\(0.84,0.79132 \ldots, 1 . \overline{3}\)
- إجابة
-
- \(0.84,1.3\)
- \(0.79132 \ldots\)
\(2.3 \overline{8}, 0.572,4.93814 \ldots\)
في التمارين التالية، حدد ما إذا كان كل رقم عقلانيًا أم غير منطقي.
- \(\sqrt{121}\)
- \(\sqrt{48}\)
- إجابة
-
- معقول
- غير منطقي
- \(\sqrt{56}\)
- \(\sqrt{16}\)
في التمارين التالية، حدد ما إذا كان كل رقم هو رقم حقيقي أم ليس رقمًا حقيقيًا.
- \(\sqrt{-9}\)
- \(-\sqrt{169}\)
- إجابة
-
- ليس رقمًا حقيقيًا
- رقم حقيقي
- \(\sqrt{-64}\)
- \(-\sqrt{81}\)
في التمارين التالية، قم بإدراج
- أرقام كاملة،
- الأعداد الصحيحة،
- أرقام عقلانية،
- أرقام غير منطقية،
- أرقام حقيقية لكل مجموعة من الأرقام.
\(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
- إجابة
-
- \(0, \sqrt{16}\)
- \(-4,0, \sqrt{16}\)
- \(-4,0, \frac{5}{6}, \sqrt{16}\)
- \(\sqrt{18}, 5.2537 \ldots\)
- \(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
\(-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}\)
حدد موقع الكسور على خط الأعداد
في التمارين التالية، حدد موقع الأرقام على خط الأعداد.
\(\frac{2}{3}, \frac{5}{4}, \frac{12}{5}\)
- إجابة
-
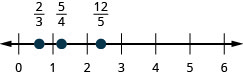
\(\frac{1}{3}, \frac{7}{4}, \frac{13}{5}\)
\(2 \frac{1}{3},-2 \frac{1}{3}\)
- إجابة
-
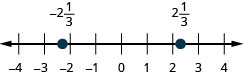
\(1 \frac{3}{5},-1 \frac{3}{5}\)
في التمارين التالية، قم بترتيب كل زوج من أزواج الأرقام التالية باستخدام < or >.
−1___\(-\frac{1}{8}\)
- إجابة
-
<
\(-3 \frac{1}{4}\)___−4
\(-\frac{7}{9}\)___\(\frac{4}{9}\)
- إجابة
-
>
\(-2\)___\(\frac{19}{8}\)
حدد موقع الأعداد العشرية على خط الأعداد
في التمارين التالية، حدد موقع خط الأعداد.
0.3
- إجابة
-
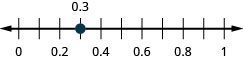
−0.2
−2.5
- إجابة
-
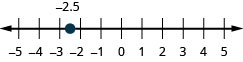
2.7
في التمارين التالية، قم بترتيب كل زوج من أزواج الأرقام التالية باستخدام < or >.
0.9___0.6
- إجابة
-
>
0.7___0.8
−0.6___−0.59
- إجابة
-
>
−0.27___−0.3
خصائص الأعداد الحقيقية
استخدم الخصائص الإبدالية والترابطية
في التمارين التالية، استخدم الخاصية الترابطية للتبسيط.
−12 (4 م)
- إجابة
-
−48 م
30\(\left(\frac{5}{6} q\right)\)
(+16) +31
- إجابة
-
+47
(ج+0.2) +0.7
في التمارين التالية، قم بالتبسيط.
6y+37+ (−6 سنوات)
- إجابة
-
37
\(\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)\)
\(\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}\)
- إجابة
-
\(\frac{35}{9}\)
\(-18 \cdot 15 \cdot \frac{2}{9}\)
\(\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}\)
- إجابة
-
1\(\frac{7}{12}\)
(3.98 دي+0.75 د) +1.25 د
11 × 8 سنة+16 × 15 عامًا
- إجابة
-
27 × 23 عامًا
52m+ (−20n) + (−18 م) + (−5n)
استخدم الهوية والخصائص العكسية للجمع والضرب
في التمارين التالية، ابحث عن المعكوس الجمعي لكل رقم.
- \(\frac{1}{3}\)
- 5.1
- \(-14\)
- \(-\frac{8}{5}\)
- إجابة
-
- \(-\frac{1}{3}\)
- \(-5.1\)
- -14
- \(-\frac{8}{5}\)
- \(-\frac{7}{8}\)
- \(-0.03\)
- 17
- \(\frac{12}{5}\)
في التمارين التالية، ابحث عن المعكوس الضربي لكل رقم.
- \(10\)
- \(-\frac{4}{9}\)
- 0.6
- إجابة
-
- \(\frac{1}{10}\)
- \(-\frac{9}{4}\)
- \(\frac{5}{3}\)
- \(-\frac{9}{2}\)
- -7
- 2.1
استخدم خصائص الصفر
في التمارين التالية، قم بالتبسيط.
83\(\cdot 0\)
- إجابة
-
0
\(\frac{0}{9}\)
\(\frac{5}{0}\)
- إجابة
-
غير محدد
\(0 \div \frac{2}{3}\)
في التمارين التالية، قم بالتبسيط.
43+39+ (−43)
- إجابة
-
39
(ن+6.75) +0.25
\(\frac{5}{13} \cdot 57 \cdot \frac{13}{5}\)
- إجابة
-
57
\(\frac{1}{6} \cdot 17 \cdot 12\)
\(\frac{2}{3} \cdot 28 \cdot \frac{3}{7}\)
- إجابة
-
8
\(9(6 x-11)+15\)
تبسيط التعبيرات باستخدام خاصية التوزيع
في التمارين التالية، قم بتبسيط استخدام خاصية التوزيع.
7 (x+9)
- إجابة
-
7x+63
9 (ص-4)
−3 (6m−1)
- إجابة
-
−18 متر+3
−8 (−7a−12)
\(\frac{1}{3}(15 n-6)\)
- إجابة
-
5n−2
\((y+10) \cdot p\)
(أ-4) - (6أ+9)
- إجابة
-
−5a-13
4 (x+3) −8 (x−7)
أنظمة القياس
1.1 تحديد وحدات القياس الأمريكية وتحويلها من وحدة إلى أخرى
في التمارين التالية، قم بتحويل الوحدات. قرِّب إلى أقرب جزء من عشرة.
يبلغ طول شجرة الأزهار 7 أقدام. قم بتحويل الارتفاع إلى بوصة.
- إجابة
-
84 بوصة
يبلغ عرض إطار الصورة 42 بوصة. قم بتحويل العرض إلى أقدام.
يبلغ طول كيلي 5 أقدام و 4 بوصات. حول ارتفاعها إلى بوصات.
- إجابة
-
64 بوصة
يبلغ عرض الملعب 45 قدمًا. قم بتحويل العرض إلى ياردات.
يبلغ ارتفاع جبل شاستا 14179 قدمًا. قم بتحويل الارتفاع إلى أميال.
- إجابة
-
2.7 أميال
يزن شامو 4.5 طن. قم بتحويل الوزن إلى رطل.
استمرت المسرحية\(1\frac{3}{4}\) لساعات. قم بتحويل الوقت إلى دقائق.
- إجابة
-
105 دقيقة
كم عدد ملاعق الطعام في ربع غالون؟
كان وزن طفل نعومي 5 أرطال 14 أوقية عند الولادة. قم بتحويل الوزن إلى أوقية.
- إجابة
-
94 أونصة
تحتاج ترينه إلى 30 كوبًا من الطلاء لمشروعها الفني في الفصل. قم بتحويل مستوى الصوت إلى جالون.
استخدم وحدات القياس المختلطة في النظام الأمريكي.
في التمارين التالية، قم بحل.
اصطاد جون 4 جراد البحر. كانت أوزان الكركند 1 رطل 9 أونصات، 1 رطل 12 أونصة، 4 أرطال 2 أوقية، و 2 رطل 15 أونصة. ما الوزن الإجمالي للكركند؟
- إجابة
-
10 رطل. 6 أوقية.
سجل بيدرو كل يوم من أيام الأسبوع الماضي عدد الدقائق التي قضاها في القراءة. كان عدد الدقائق 50، 25، 83، 45، 32، 60، 135. كم عدد الساعات التي قضاها بيدرو في القراءة؟
يبلغ طول فؤاد 6 أقدام وبوصتين. إذا كان يقف على درجة سلم بارتفاع 8 أقدام و10 بوصات، فما ارتفاع قمة رأس فؤاد عن الأرض؟
- إجابة
-
15 قدمًا
تريد داليلا صنع أغطية الوسائد. يستغرق كل غطاء 30 بوصة من القماش. كم ياردة من القماش تحتاجها لأربعة أغطية؟
قم بإجراء تحويلات الوحدات في النظام المتري
في التمارين التالية، قم بتحويل الوحدات.
يبلغ طول دونا 1.7 متر. حول ارتفاعها إلى سنتيمترات.
- إجابة
-
170 سنتيمترًا
يبلغ ارتفاع جبل إيفرست 8850 مترًا. قم بتحويل الارتفاع إلى الكيلومترات.
يحتوي كوب واحد من الزبادي على 488 ملليغرام من الكالسيوم. قم بتحويل هذا إلى جرامات.
- إجابة
-
0.488 غرامًا
يحتوي كوب واحد من الزبادي على 13 جرامًا من البروتين. قم بتحويل هذا إلى مليغرام.
كان وزن سيرجيو 2.9 كجم عند الولادة. قم بتحويل هذا إلى جرامات.
- إجابة
-
2,900 جرام
زجاجة ماء تحتوي على 650 مليلتر. قم بتحويل هذا إلى لترات.
استخدم وحدات القياس المختلطة في النظام المتري
في التمارين التالية، قم بحل.
يبلغ طول مينه مترين. يبلغ طول ابنته 88 سم. كم يبلغ طول مينه من ابنته؟
- إجابة
-
1.12 متر
كان لدى سلمى زجاجة مياه سعة 1 لتر. إذا شربت ١٤٥ مليلترًا، فما مقدار الماء المتبقي في الزجاجة؟
تحتوي حصة واحدة من عصير التوت البري على 30 جرامًا من السكر. ما عدد الكيلوجرامات من السكر في 30 حصة من عصير التوت البري؟
- إجابة
-
0.9 كيلوغرام
قدمت أونصة واحدة من التوفو 2 جرام من البروتين. ما عدد الملليغرامات من البروتين التي توفرها 5 أونصات من التوفو؟
التحويل بين الولايات المتحدة والأنظمة المترية للقياس
في التمارين التالية، قم بإجراء تحويلات الوحدات. قرِّب إلى أقرب جزء من عشرة.
يبلغ طول ماجد 69 بوصة. حول ارتفاعه إلى سنتيمترات.
- إجابة
-
175.3 سنتيمترًا
يبلغ طول ملعب كرة السلة الجامعي 84 قدمًا. حول هذا الطول إلى أمتار.
مشيت كارولين 2.5 كيلومتر. حول هذا الطول إلى أميال.
- إجابة
-
1.6 أميال
يزن لوكاس 78 كيلوجرامًا. حول وزنه إلى رطل.
تحتوي سيارة ستيف على 55 لترًا من الغاز. قم بتحويل هذا إلى جالون.
- إجابة
-
14.6 جالون
يزن صندوق الكتب 25 رطلاً. حول الوزن إلى الكيلوجرامات.
التحويل بين درجات الحرارة الفهرنهايت والدرجة المئوية
في التمارين التالية، قم بتحويل درجات حرارة فهرنهايت إلى درجات مئوية. قرِّب إلى أقرب جزء من عشرة.
95 درجة فهرنهايت
- إجابة
-
35 درجة مئوية
23 درجة فهرنهايت
20 درجة فهرنهايت
- إجابة
-
—6.7 درجة مئوية
64 درجة فهرنهايت
في التمارين التالية، قم بتحويل درجات الحرارة المئوية إلى درجات فهرنهايت. قرِّب إلى أقرب جزء من عشرة.
30 درجة مئوية
- إجابة
-
86 درجة فهرنهايت
—5 درجة مئوية
-12 درجة مئوية
- إجابة
-
10.4 درجة فهرنهايت
24 درجة مئوية
اختبار ممارسة الفصل
اكتب عددًا صحيحًا باستخدام الأرقام: مائتان وخمسة آلاف وستمائة وسبعة عشر.
- إجابة
-
205,617
أوجد التحليل الأولي للعدد ٥٠٤.
أوجد المضاعف المشترك الأصغر للعددين ١٨ و٢٤.
- إجابة
-
72
اجمع بين المصطلحات المشابهة: 5n+8+2n−1.
في التمارين التالية، قم بالتقييم.
\(-|x|\)عندما\(x=-2\)
- إجابة
-
−2
11-a عندما a = −3
ترجم إلى تعبير جبري وقم بتبسيط: أقل بعشرين من سالب 7.
- إجابة
-
−7−20؛ −27
تمتلك مونك رصيدًا قدره -18 دولارًا في حسابها الجاري. إنها تودع 152 دولارًا في الحساب. ما هو الرصيد الجديد؟
قرِّب ٦٧٧٫١٣٤٨ لأقرب جزء من مائة.
- إجابة
-
677.13
قم\(\frac{4}{5}\) بالتحويل إلى رقم عشري.
قم بتحويل 1.85 إلى نسبة مئوية.
- إجابة
-
185%
حدد الموقع\(\frac{2}{3},-1.5,\)\(\frac{9}{4}\) وعلى خط الأرقام.
في التمارين التالية، قم بتبسيط كل تعبير.
\(4+10(3+9)-5^{2}\)
- إجابة
-
99
−85+42
−19-25
- إجابة
-
−44
\((-2)^{4}\)
\(-5(-9) \div 15\)
- إجابة
-
3
\(\frac{3}{8} \cdot \frac{11}{12}\)
\(\frac{4}{5} \div \frac{9}{20}\)
- إجابة
-
\(\frac{16}{9}\)
\(\frac{12+3 \cdot 5}{15-6}\)
\(\frac{m}{7}+\frac{10}{7}\)
- إجابة
-
\(\frac{m+10}{7}\)
\(\frac{7}{12}-\frac{3}{8}\)
\(-5.8+(-4.7)\)
- إجابة
-
−10.5
100-64.25
(0.07) (31.95)
- إجابة
-
2.2365
\(9 \div 0.05\)
\(-14\left(\frac{5}{7} p\right)\)
- إجابة
-
−10 ص
(+ 8) −9
6x+ (−4 سنوات) +9x+8y
- إجابة
-
15 × 4 سنوات
\(\frac{0}{23}\)
\(\frac{75}{0}\)
- إجابة
-
غير محدد
−2 (13q−5)
استمر الفيلم لمدة\(\frac{2}{3}\) ساعة. كم عدد الدقائق التي استغرقتها؟ (1 ساعة\(=60\) دقيقة)
- إجابة
-
100 دقيقة
يبلغ طول سيارة مايك الرياضية متعددة الاستخدامات 5 أقدام و 11 بوصة. يريد وضع حقيبة شحن على السطح على سيارة الدفع الرباعي. يبلغ طول حقيبة الشحن 1 قدم و 6 بوصات. ماذا سيكون الارتفاع الإجمالي لسيارات الدفع الرباعي مع حقيبة البضائع على السطح؟ (1 قدم = 12 بوصة)
ركضت جينيفر 2.8 ميل. حول هذا الطول إلى كيلومترات. (ميل واحد = 1.61 كيلومتر)
- إجابة
-
4.508 كم


