1.8: الأرقام العشرية

Last updated

Nov 1, 2022
Page ID
200721
Save as PDF
- 1.7E: تمارين
- 1.8E: تمارين

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

اسم الأعداد العشرية وكتابتها
الأرقام العشرية المستديرة
جمع الأعداد العشرية وطرحها
ضرب الأرقام العشرية وقسمتها
تحويل الأعداد العشرية والكسور والنسب المئوية

ملاحظة

يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي يتم تناولها في هذا القسم في فصل ما قبل الجبر، الكسور العشرية.

اسم الأعداد العشرية وكتابتها

الأعداد العشرية هي طريقة أخرى لكتابة الكسور s التي مقاماتها هي قوى العدد 10.

$\begin{array} {ll} {0.1 = \frac { 1 } { 10 }} &{0.1 \text { is "one tenth" }} \\ {0.01 = \frac { 1 } { 100 }} &{0.01 \text { is "one hundredth }} \\ {0.001 = \frac { 1 } { 1,000 }} &{0.001 \text { is "one thousandth }} \\ {0.0001 = \frac { 1 } { 10,000 }} &{0.0001 \text { is "one ten-thousandth" }} \end{array}$

لاحظ أن «عشرة آلاف» هو رقم أكبر من واحد، ولكن «واحد من عشرة آلاف» هو رقم أصغر من واحد. تخبرك «th» في نهاية الاسم أن الرقم أصغر من واحد.

عندما نسمي رقمًا صحيحًا، يتوافق الاسم مع القيمة المكانية بناءً على قوى العشرة. نقرأ 10,000 كـ «عشرة آلاف» و 10,000,000 كـ «عشرة ملايين». وبالمثل، تتوافق أسماء المنازل العشرية مع قيم الكسور الخاصة بها. $\PageIndex{1}$ يعرض الشكل أسماء القيم المكانية على يسار ويمين العلامة العشرية.

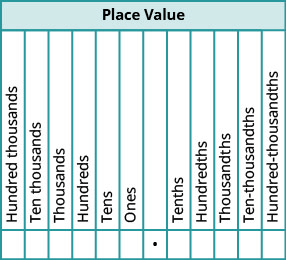
يتم عرض جدول بعنوان القيمة المكانية. من اليسار إلى اليمين كتب على الصف «مائة ألف» و «عشرة آلاف» و «الآلاف» و «المئات» و «العشرات» و «الآحاد». ثم توجد خلية فارغة وأسفلها نقطة عشرية. على يمين هذا النص، كتب على الخلايا «الأعشار» و «المئات» و «الألف» و «عشرة آلاف» و «المئات من الألف». — الشكل $\PageIndex{1}$ : تظهر القيمة المكانية للأرقام العشرية على يسار ويمين النقطة العشرية.

التمارين $\PageIndex{1}$

قم بتسمية الرقم العشري $4.3$ .

إجابة: $يتم إعطاء جدول بأربع خطوات. بالإضافة إلى ذلك، يتم إعطاء الرقم 4.3. تقول الخطوة الأولى «الخطوة 1. قم بتسمية الرقم على يسار الفاصلة العشرية.» على يمين هذا، يُلاحظ أن «4 على يسار النقطة العشرية». على يمين هذا النص، يُقرأ «أربعة» متبوعًا بمساحة فارغة كبيرة.$ $الخطوة الثانية تقرأ «الخطوة 2. اكتب 'و' للفاصلة العشرية.» على يمين هذا النص مكتوب «أربعة و» متبوعًا بمساحة فارغة.$ $الخطوة الثالثة تقرأ «الخطوة 3. قم بتسمية جزء 'الرقم' على يمين العلامة العشرية كما لو كان رقمًا صحيحًا.» على يمين هذا النص، مكتوب عليه «الرقم 3 على يمين العلامة العشرية». على يمين هذا النص، يُقرأ «أربعة وثلاثة» متبوعًا بفراغ.$ $أخيرًا، تنص الخطوة الأخيرة على «الخطوة 4. قم بتسمية المكان العشري.» على يمين هذا النص، مكتوب عليه «أربعة وثلاثة أعشار».$

التمارين $\PageIndex{2}$

قم بتسمية الرقم العشري $6.7$ .

إجابة: ستة وسبعة أعشار

التمارين $\PageIndex{3}$

قم بتسمية الرقم العشري $5.8$ .

إجابة: خمسة وثمانية أعشار

نلخص الخطوات اللازمة لتسمية عدد عشري أدناه.

قم بتسمية رقم عشري.

قم بتسمية الرقم على يسار الفاصلة العشرية.
اكتب «و» للفاصلة العشرية.
قم بتسمية جزء «الرقم» على يمين العلامة العشرية كما لو كان رقمًا صحيحًا.
قم بتسمية المكان العشري للرقم الأخير.

التمارين $\PageIndex{4}$

قم بتسمية الرقم العشري: $−15.571$ .

إجابة

	$−15.571$
قم بتسمية الرقم على يسار الفاصلة العشرية.	سالب خمسة عشر __________________________
اكتب «و» للفاصلة العشرية.	سالب خمسة عشر و ______________________________
قم بتسمية الرقم على يمين الفاصلة العشرية.	سالب خمسة عشر وخمسمائة وواحد وسبعون __________
$1$ هو في مكان الألف.	سالب خمسة عشر وخمسمائة وواحد وسبعون ألف

التمارين $\PageIndex{5}$

قم بتسمية الرقم العشري: $−13.461$ .

إجابة: سالب ثلاثة عشر وأربعمائة وواحد وستون ألف

التمارين $\PageIndex{6}$

قم بتسمية الرقم العشري: $−2.053$ .

إجابة: سالب اثنين وثلاثة وخمسون جزءًا من ألف

عندما نكتب شيكًا نكتب كل من الأرقام واسم الرقم. دعونا نرى كيفية كتابة الرقم العشري من الاسم.

التمارين $\PageIndex{7}$ : How to Write decimals

اكتب «أربعة عشر وأربعة وعشرين جزءًا من ألف» في صورة عدد عشري.

إجابة: $يتم إعطاء جدول بأربع خطوات. تقول الخطوة الأولى «الخطوة 1. ابحث عن العمل 'و' - فهو يحدد العلامة العشرية. ضع علامة عشرية تحت الكلمة «and». ترجم الكلمات قبل 'و' إلى الرقم الصحيح ثم ضعه على يسار الفاصلة العشرية.» على يمين هذا، لدينا عبارة «أربعة عشر وأربعة وعشرين ألفًا». أسفل هذه الكلمة، لدينا «أربعة عشر وأربعة وعشرين ألفًا» مع تسطير كلمة «و». أسفل هذه الكلمة، لدينا مساحة فارغة صغيرة مفصولة عن مساحة فارغة أكبر بنقطة عشرية. تحت هذا، لدينا 14 في المساحة الفارغة الصغيرة متبوعة بالفاصلة العشرية والمساحة الفارغة الأكبر.$ $الخطوة الثانية تقرأ «الخطوة 2. حدد عدد المنازل العشرية المطلوبة على يمين الفاصلة العشرية من خلال ملاحظة القيمة المكانية المشار إليها بالكلمة الأخيرة.» على يمين هذا مكتوب «الكلمة الأخيرة هي جزء من الألف». على يمين هذا الرقم 14 متبوعًا بنقطة عشرية وثلاث مسافات فارغة صغيرة. تحت المساحات الفارغة، تتم كتابة الكلمات «أعشار» و «أجزاء من مائة» و «جزء من ألف».$ $الخطوة الثالثة تقرأ «الخطوة 3. ترجم الكلمات بعد 'و' إلى الرقم الموجود على يمين الفاصلة العشرية. اكتب الرقم في المسافات - ضع الرقم الأخير في المكان الأخير.» على يمين هذا، لدينا 14 متبوعًا بعدد عشري متبوعًا بمسافة فارغة متبوعة ب2 و 4 على الفراغين الآخرين السابقين.$ $أخيرًا، تنص الخطوة الأخيرة على «الخطوة 4. املأ الأصفار لحوامل الأماكن الفارغة حسب الحاجة.» على يمين هذا النص، مكتوب عليه «الأصفار مطلوبة في مكان الأعشار». على يمين هذا العدد، لدينا 14 متبوعًا بنقطة عشرية متبوعة بـ 0 و2 و4 على التوالي في المساحات الفارغة. أدناه، لدينا «أربعة عشر وأربعة وعشرين ألفًا مكتوبًا 14.024".$

التمارين $\PageIndex{8}$

اكتب العدد العشري: ثلاثة عشر وثمانية وستين جزءًا من ألف.

إجابة: 13.068

التمارين $\PageIndex{9}$

اكتب العدد العشري: خمسة وأربعة وتسعون جزءًا من ألف.

إجابة: 5.094

نحن نلخص الخطوات لكتابة عدد عشري.

اكتب عددًا عشريًا.

ابحث عن الكلمة «و» —فهي تحدد العلامة العشرية.
- ضع نقطة عشرية تحت الكلمة «and». ترجم الكلمات قبل «و» إلى الرقم الصحيح ووضعه على يسار العلامة العشرية.
- إذا لم يكن هناك «و»، فاكتب «0" بنقطة عشرية على يمينها.
حدد عدد المنازل العشرية المطلوبة على يمين الفاصلة العشرية من خلال ملاحظة القيمة المكانية المشار إليها بالكلمة الأخيرة.
ترجم الكلمات بعد «و» إلى الرقم الموجود على يمين العلامة العشرية. اكتب الرقم في المسافات - ضع الرقم النهائي في المكان الأخير.
املأ الأصفار لحوامل الأماكن حسب الحاجة.

الأعداد العشرية المستديرة

تقريب الأعداد العشرية يشبه إلى حد كبير تقريب الأرقام الصحيحة. سنقوم بتقريب الأعداد العشرية باستخدام طريقة تستند إلى الطريقة التي استخدمناها لتقريب الأعداد الصحيحة.

التمارين $\PageIndex{10}$

قرِّب ١٨٫٣٧٩ لأقرب جزء من مائة.

إجابة: $يتم إعطاء جدول بأربع خطوات. تقرأ الخطوة الأولى «الخطوة 1: حدد القيمة المكانية المحددة وقم بتمييزها بسهم.» على يمين هذا، لدينا الرقم 18.379؛ وفوقه توجد الكلمات في خانة المئات، والتي تحتوي على سهم يشير إلى الرقم 7.$ $الخطوة الثانية تقرأ «الخطوة 2. ضع خطًا تحت الرقم الموجود على يمين القيمة المكانية المحددة.» على يمين هذا، لدينا 18.379 مع 9 مسطر.$ $الخطوة الثالثة تقرأ «الخطوة 3. هل هذا الرقم أكبر من أو يساوي 5؟ فيما يلي نص هذا: «نعم: أضف 1 إلى الرقم في القيمة المكانية المحددة.» فيما يلي نص هذا: «لا: لا تقم بتغيير الرقم في القيمة المكانية المحددة.» على يمين هذا، تقول «لأن 9 أكبر من أو يساوي» على يمين هذا، لدينا الرقم 18.379 مع علامة 9 التي تحمل علامة «حذف» و 7 بعلامة «إضافة 1".$ $أخيرًا، تنص الخطوة الأخيرة على «الخطوة 4. أعد كتابة الرقم، مع إزالة جميع الأرقام الموجودة على يمين رقم التقريب.» على يمين هذا، لدينا 18.38 متبوعًا بـ «18.38 هو 18.379 مقربًا لأقرب جزء من مائة.»$

التمارين $\PageIndex{11}$

قرِّب لأقرب جزء من مائة: 1.047.

إجابة: 1.05

التمارين $\PageIndex{12}$

قرِّب لأقرب جزء من مائة: 9.173.

إجابة: 9.17

نلخص خطوات تقريب الرقم العشري هنا.

الأرقام العشرية المستديرة.

حدد القيمة المكانية المحددة وقم بتمييزها بسهم.
ضع خط تحت الرقم الموجود على يمين القيمة المكانية.
هل هذا الرقم أكبر من أو يساوي 5؟
- نعم - أضف 1 إلى الرقم في القيمة المكانية المحددة.
- لا - لا تقم بتغيير الرقم في القيمة المكانية المحددة.
أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب.

التمارين $\PageIndex{13}$

قرِّب 18.379 إلى الأقرب

العاشر
رقم صحيح.

إجابة

الجولة 18.379

1. إلى أقرب جزء من عشرة

حدد موقع المكان العاشر بسهم.	$.$
ضع خط تحت الرقم الموجود على يمين القيمة المكانية المحددة.	$.$
ولأن 7 أكبر من أو يساوي 5، أضف 1 إلى 3.	$.$
أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب.	$.$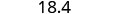
لاحظ أن الأرقام المحذوفة لم يتم استبدالها بالأصفار.	لذا، فإن مبلغ 18.379 الذي تم تقريبه إلى أقرب جزء من عشرة يساوي 18.4.

2. إلى أقرب رقم صحيح

حدد مكان تلك باستخدام سهم.	$.$
ضع خط تحت الرقم الموجود على يمين القيمة المكانية المحددة.	$.$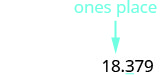
نظرًا لأن 3 لا يزيد عن أو يساوي 5، فلا تضيف 1 إلى 8.	$.$
أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب.	$.$
	إذن، تم تقريب 18.379 إلى أقرب عدد صحيح هو 18.

التمارين $\PageIndex{14}$

قرِّب ٦٫٥٨٢ إلى الأقرب

جزء من مئة
العاشر
رقم صحيح.

إجابة

6.58
6.6
7

التمارين $\PageIndex{15}$

قرِّب 15.2175 إلى الأقرب

جزء من ألف
جزء من مئة
العاشر.

إجابة

15.218
15.22
15.2

جمع الأعداد العشرية وطرحها

لجمع أو طرح الكسور العشرية، نقوم بمحاذاة النقاط العشرية. من خلال ترتيب النقاط العشرية بهذه الطريقة، يمكننا إضافة أو طرح قيم المكان المقابلة. ثم نقوم بعد ذلك بإضافة الأرقام أو طرحها كما لو كانت أعدادًا صحيحة ثم نضع الفاصلة العشرية في المجموع.

قم بإضافة أو طرح الأرقام العشرية.

اكتب الأرقام بحيث تصطف النقاط العشرية رأسيًا.
استخدم الأصفار كحوامل، حسب الحاجة.
قم بإضافة الأرقام أو طرحها كما لو كانت أرقامًا صحيحة. ثم ضع النقطة العشرية في الإجابة تحت النقاط العشرية في الأرقام المعطاة.

التمارين $\PageIndex{16}$

إضافة: $23.5+41.38$ .

إجابة: $\text{Write the numbers so that the decimal points line up vertically.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}$
$\text{Put 0 as a placeholder after the 5 in 23.5. Remember, } \frac{5}{10} = \frac{50}{100}, \text{ so } 0.5 = 0.50 \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}$
$\text{Add the numbers as if they were whole numbers . Then place the decimal point in the sum.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline 64.88 \end{array}$

التمارين $\PageIndex{17}$

إضافة: $4.8+11.69$ .

إجابة: $16.49$

التمارين $\PageIndex{18}$

إضافة: $5.123+18.47$ .

إجابة: $23.593$

التمارين $\PageIndex{19}$

طرح: $20−14.65$ .

إجابة: $\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {20 - 14.65} \\ {20.} \\ {-14.65} \\ \hline \end{align}} \\ {\text{Remember, 20 is a whole number, so place the decimal point after the 0.}} &{} \end{array}$
$\begin{array} {ll} {\text{Put zeros to the right as placeholders.}} &{ \begin{align} {20.00} \\ {-14.65} \\ \hline \end{align}} \end{array}$
$\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {\tiny{9} \quad \tiny{9}\qquad} \\ {\small{1} \not{\small{10}} \not{\small10}\not{\small10}}\\ {\not{2}\not{0.}\not{0}\not{0}} \\ {-14.65} \\ \hline \\{5.35} \end{align}} \end{array}$

التمارين $\PageIndex{20}$

طرح: $10−9.58$ .

إجابة: 0.42

التمارين $\PageIndex{21}$

طرح: $50−37.42$ .

إجابة: 12.58

ضرب الأعداد العشرية وقسمتها

ضرب الأعداد العشرية يشبه إلى حد كبير ضرب الأعداد الصحيحة - علينا فقط تحديد مكان وضع العلامة العشرية. سيكون إجراء ضرب الأعداد العشرية منطقيًا إذا قمنا بتحويلها أولاً إلى كسور ثم ضربها.

لذلك دعونا نرى ما سنحصل عليه كناتج الأعداد العشرية من خلال تحويلها إلى كسور أولاً. سنقوم بعمل مثالين جنبًا إلى جنب. ابحث عن النمط!

طاولة $\PageIndex{1}$
	$.$
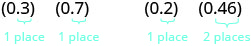قم بالتحويل إلى كسور.	$.$
اضرب.	$.$
قم بالتحويل إلى أرقام عشرية.	$.$

لاحظ، في المثال الأول، أننا ضربنا رقمين يحتوي كل منهما على رقم واحد بعد العلامة العشرية وكان المنتج يحتوي على منزلتين عشريتين. في المثال الثاني، قمنا بضرب رقم ذي منزلة عشرية واحدة في رقم يحتوي على منزلتين عشريتين وكان المنتج يحتوي على ثلاث منازل عشرية.

نضرب الأرقام تمامًا كما نفعل الأعداد الصحيحة، متجاهلين النقطة العشرية مؤقتًا. ثم نحسب بعد ذلك عدد النقاط العشرية في العوامل ويخبرنا هذا المجموع بعدد المنازل العشرية في المنتج.

تنطبق قواعد ضرب الأرقام الموجبة والسالبة على الكسور العشرية أيضًا بالطبع!

عند ضرب رقمين،

إذا كانت علاماتها هي نفسها، يكون المنتج إيجابيًا.
إذا كانت علاماتها مختلفة، يكون المنتج سلبيًا.

عندما نضرب الأعداد العشرية الموقعة، نحدد أولاً علامة المنتج ثم نضرب كما لو كان كلا الرقمين موجبين. أخيرًا، نكتب المنتج بالعلامة المناسبة.

ضرب الأعداد العشرية.

حدد علامة المنتج.
اكتب في شكل عمودي، واصطف الأرقام على اليمين. اضرب الأرقام كما لو كانت أرقامًا كاملة، مع تجاهل النقاط العشرية مؤقتًا.
ضع النقطة العشرية. عدد المنازل العشرية في المنتج هو مجموع عدد المنازل العشرية في العوامل.
اكتب المنتج بالعلامة المناسبة.

التمارين $\PageIndex{22}$

اضرب: $(−3.9)(4.075)$ .

إجابة

	$(−3.9)(4.075)$
العلامات مختلفة. سيكون المنتج سلبيًا.
اكتب في شكل عمودي، واصطف الأرقام على اليمين.	$.$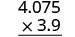
اضرب.	$.$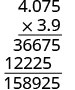
أضف عدد المنازل العشرية في العوامل $(1 + 3)$ . $.$ ضع العلامة العشرية على بعد 4 أماكن من اليمين.	$.$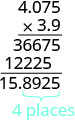
العلامات مختلفة، وبالتالي فإن المنتج سلبي.	$(−3.9)(4.075) = −15.8925$

التمارين $\PageIndex{23}$

اضرب: $−4.5(6.107)$ .

إجابة: $−27.4815$

التمارين $\PageIndex{24}$

اضرب: −10.79 (8.12).

إجابة: $−87.6148$

في العديد من فصولك الأخرى، خاصة في العلوم، ستضرب الأرقام العشرية بقوى 10 (10، 100، 1000، إلخ). إذا قمت بضرب بعض المنتجات على الورق، فقد تلاحظ نمطًا يربط عدد الأصفار بقوة 10 بعدد المنازل العشرية، وننقل العلامة العشرية إلى اليمين للحصول على المنتج.

اضرب عددًا عشريًا في قوة عشرة.

انقل النقطة العشرية إلى اليمين بنفس عدد الأماكن مثل عدد الأصفار بقوة 10.
أضف الأصفار في نهاية الرقم حسب الحاجة.

التمارين $\PageIndex{25}$

اضرب 5.63

قبل 10
بحلول 100
بنسبة 1,000.

إجابة

بالنظر إلى عدد الأصفار في مضاعف العشرة، نرى عدد الأماكن التي نحتاج إليها لنقل العدد العشري إلى اليمين.

ⓐ

	$5.63(10)$
يوجد صفر واحد في 10، لذا انقل العلامة العشرية مكانًا واحدًا إلى اليمين.	$.$

ⓑ

	$5.63(100)$
يوجد صفران في 100، لذا انقل العلامة العشرية مرتين إلى اليمين.	$.$

ⓒ


يوجد ٣ أصفار في ١٠٠٠، لذا انقل العلامة العشرية ٣ منازل إلى اليمين.	$.$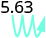
يجب إضافة صفر في النهاية.	$.$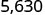

التمارين $\PageIndex{26}$

اضرب 2.58

قبل 10
بحلول 100
بنسبة 1,000.

إجابة

25.8
258
2,580

التمارين $\PageIndex{27}$

اضرب 14.2

قبل 10
بحلول 100
بنسبة 1,000.

إجابة

142
1,420
14,200

تمامًا كما هو الحال مع الضرب، فإن قسمة الأعداد العشرية تشبه إلى حد كبير قسمة الأعداد الصحيحة. علينا فقط معرفة أين يجب وضع العلامة العشرية.

لقسمة الأعداد العشرية، حدد قوة العدد ١٠ لضرب المقام لجعله عددًا صحيحًا. ثم اضرب البسط بنفس قوة 10. بسبب خاصية الكسور المتكافئة، لم نغير قيمة الكسر! التأثير هو نقل النقاط العشرية في البسط والمقام بنفس عدد الأماكن إلى اليمين. على سبيل المثال:

$\begin{array} { c } { \frac { 0.8 } { 0.4 } } \\ { \frac { 0.8 ( 10 ) } { 0.4 ( 10 ) } } \\ { \frac { 8 } { 4 } } \end{array}$

نحن نستخدم قواعد قسمة الأرقام الموجبة والسالبة بالأرقام العشرية أيضًا. عند قسمة الأعداد العشرية الموقعة، حدد أولاً علامة خارج القسمة ثم قسّم كما لو كان كلا الرقمين موجبين. أخيرًا، اكتب حاصل القسمة مع العلامة المناسبة.

نقوم بمراجعة الرموز والمفردات الخاصة بالقسمة:

$\begin{array} {ll} {} &{\underset{\text{quotient}}{c}} \\ {\underset{\text{dividend}}{a} \div \underset{\text{divisor}}{b} = \underset{\text{quotient}}{c}} & {\underset{\text{divisor}}{b})\overline{\underset{\text{dividend}}{a}}} \end{array}$

سنكتب الخطوات التي يجب اتخاذها عند قسمة الأرقام العشرية، لسهولة الرجوع إليها.

قسمة الأرقام العشرية.

حدد علامة حاصل القسمة.
اجعل المقسوم رقمًا صحيحًا عن طريق «نقل» العلامة العشرية إلى اليمين. «انقل» النقطة العشرية في التوزيعات بنفس عدد المواضع - بإضافة الأصفار حسب الحاجة.
يقسم. ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات.
اكتب حاصل القسمة مع العلامة المناسبة.

التمارين $\PageIndex{28}$

يقسم: $−25.65\div (−0.06)$ .

إجابة

تذكر أنه يمكنك «نقل» الأعداد العشرية في المقسوم وتوزيع الأرباح بسبب خاصية الكسور المتكافئة.

	$−25.65\div (−0.06)$
العلامات هي نفسها.	حاصل القسمة إيجابي.
اجعل المقسوم رقمًا صحيحًا عن طريق «نقل» العلامة العشرية إلى اليمين.
«انقل» النقطة العشرية في التوزيعات بنفس عدد الأماكن.	$.$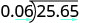
يقسم. ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات.	$.$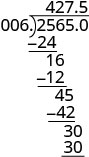
اكتب حاصل القسمة مع العلامة المناسبة.	$−25.65\div (−0.06) = 427.5$

التمارين $\PageIndex{29}$

يقسم: $−23.492\div (−0.04)$ .

إجابة: 687.3

التمارين $\PageIndex{30}$

يقسم: $−4.11\div(−0.12)$ .

إجابة: 34.25

أحد التطبيقات الشائعة لتقسيم الأرقام الصحيحة إلى أعداد عشرية هو عندما نريد العثور على سعر عنصر واحد يتم بيعه كجزء من حزمة متعددة. على سبيل المثال، لنفترض أن تكلفة علبة 24 زجاجة مياه $$3.99$ . لمعرفة سعر زجاجة ماء واحدة، سنقسم $$3.99$ على 24. نعرض هذا التقسيم في التمرين $\PageIndex{31}$ . في الحسابات باستخدام المال، سنقرّب الإجابة إلى أقرب سنت (جزء من مائة).

التمارين $\PageIndex{31}$

يقسم: $$3.99\div 24$ .

إجابة

يُعطى 0.99 مقسومًا على 24. تم إعداد مشكلة القسمة الطويلة بقسمة 24 على 3.99. يوجد جدول يتضمن الاتجاهات على اليسار والخطوات الرياضية على اليمين. تنص الخطوة الأولى على ما يلي: «ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات. قسّم كالمعتاد. متى نتوقف؟ نظرًا لأن هذا التقسيم يشمل المال، فإننا نقربه إلى أقرب سنت (جزء من مائة). وللقيام بذلك، يجب أن ننقل التقسيم إلى مكان الألف». على يمين هذا، لدينا مشكلة القسمة الطويلة التي تم إعدادها باستخدام 24 قسمة 3.990. يتم إعطاء حاصل القسمة على أنه 0.166. لإظهار العمل، تحت 3.990، يقرأ 24، الخط الأفقي الصلب، 159، 144، الخط الأفقي الصلب، 150، 144، الخط الأفقي الصلب، وأخيرًا 6. الخطوة الخامسة تقرأ «قرِّب إلى أقرب سنت». على يمين هذا، لدينا 0.166 دولارًا يساوي تقريبًا 0.17 دولارًا، وبالتالي >.99 مقسومًا على 24 هو 0.17 دولارًا». >

	$$3.99\div 24$
ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات.
قسّم كالمعتاد. متى نتوقف؟ نظرًا لأن هذا التقسيم يشمل المال، فإننا نقربه إلى أقرب سنت (جزء من مائة). للقيام بذلك، يجب أن نحمل التقسيم إلى مكان الألف.	$.$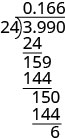
قم بالتقريب إلى أقرب سنت.	$$0.166\approx $0.17$ $$3.99\div 2\approx $0.17$

التمارين $\PageIndex{32}$

يقسم: $$6.99\div 36$ .

إجابة: $$0.19$

التمارين $\PageIndex{33}$

يقسم: $$4.99\div 12$ .

إجابة: $$0.42$

تحويل الأعداد العشرية والكسور والنسب المئوية

نقوم بتحويل الأعداد العشرية إلى كسور من خلال تحديد القيمة المكانية للرقم الأخير (أقصى اليمين). في العدد العشري 0.03، يكون الرقم 3 في خانة المئات، وبالتالي فإن 100 هو مقام الكسر المكافئ لـ 0.03.

$00.03 = \frac { 3 } { 100 }$

لاحظ أنه عندما يكون الرقم الموجود على يسار العلامة العشرية صفرًا، نحصل على كسر يكون بسطه أقل من مقامه. مثل هذه الكسور تسمى الكسور الصحيحة.

يتم تلخيص الخطوات التي يجب اتخاذها لتحويل عدد عشري إلى كسر في مربع الإجراءات.

قم بتحويل عدد عشري إلى كسر مناسب.

حدد القيمة المكانية للرقم النهائي.
اكتب الكسر.
- البسط - «الأرقام» الموجودة على يمين العلامة العشرية
- القاسم - القيمة المكانية المقابلة للرقم النهائي

التمارين $\PageIndex{34}$

اكتب 0.374 ككسر.

إجابة

	0.374
حدد القيمة المكانية للرقم النهائي.	$.$
اكتب الكسر لـ 0.374: البسط هو 374. القاسم هو 1000.	$\dfrac{374}{1000}$
قم بتبسيط الكسر.	$\dfrac{2\cdot 187}{2\cdot 500}$
قسّم العوامل المشتركة.	$\dfrac{187}{500}$ لذلك، $0.374=\dfrac{187}{500}$

هل لاحظت أن عدد الأصفار في المقام $\dfrac{374}{1000}$ يساوي عدد المنازل العشرية في 0.374؟

التمارين $\PageIndex{35}$

اكتب 0.234 ككسر.

إجابة: $\dfrac{117}{500}$

التمارين $\PageIndex{36}$

اكتب 0.024 ككسر.

إجابة: $\dfrac{3}{125}$

لقد تعلمنا تحويل الأعداد العشرية إلى كسور. الآن سنقوم بعمل العكس - تحويل الكسور إلى أعداد عشرية. تذكر أن شريط الكسر يعني القسمة. لذلك $\dfrac{4}{5}$ يمكن كتابتها $4\div 5$ أو $5)\overline{4}$ . يؤدي هذا إلى الطريقة التالية لتحويل الكسر إلى عدد عشري.

قم بتحويل كسر إلى رقم عشري.

لتحويل كسر إلى رقم عشري، قسّم بسط الكسر على مقام الكسر.

التمارين $\PageIndex{37}$

اكتب $-\dfrac{5}{8}$ في صورة عدد عشري.

إجابة

نظرًا لأن شريط الكسر يعني القسمة، فإننا نبدأ بالكتابة $\dfrac{5}{8}$ كـ $8)\overline{5}$ . الآن قسّم.

$هذه مشكلة قسمة طويلة حيث يكون 8 قسمة 5.000 و0.625 كحاصل القسمة. تحت 5.000 لدينا 48، وخط أفقي صلب، 20، 16، خط أفقي صلب، 40، 40، وخط أفقي نهائي. إذن خمسة أثمان تساوي 0.625.$

التمارين $\PageIndex{38}$

اكتب $-\dfrac{7}{8}$ في صورة عدد عشري.

إجابة: −0.875

التمارين $\PageIndex{39}$

اكتب $-\dfrac{3}{8}$ في صورة عدد عشري.

إجابة: −0.375

عندما نقسم، لن نحصل دائمًا على رصيد صفري. في بعض الأحيان ينتهي حاصل القسمة بعدد عشري يتكرر. الرقم العشري المتكرر هو رقم عشري يتكرر فيه الرقم الأخير أو مجموعة الأرقام إلى ما لا نهاية. يتم وضع شريط فوق كتلة الأرقام المتكررة للإشارة إلى تكرارها.

تكرار العدد العشري

الرقم العشري المتكرر هو رقم عشري يتكرر فيه الرقم الأخير أو مجموعة الأرقام إلى ما لا نهاية.

يتم وضع شريط فوق كتلة الأرقام المتكررة للإشارة إلى تكرارها.

التمارين $\PageIndex{40}$

اكتب $\dfrac{43}{22}$ في صورة عدد عشري.

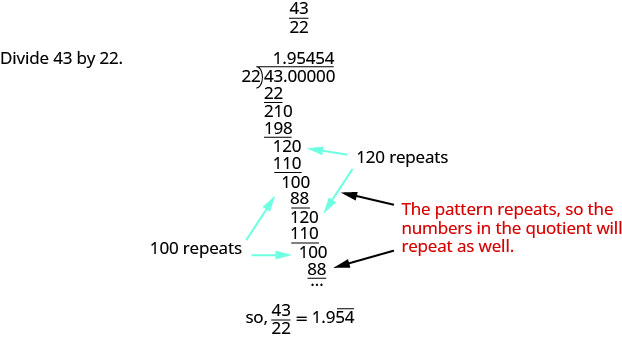
إجابة: $تم إعطاء الرقم 43/22. يتم إعطاء التوجيه لـ «تقسيم 43 على 22". تُعطى مشكلة القسمة المطولة بقسمة 22 على 43.00000 على 1.95454 كحاصل القسمة. تحت 43.00000 لدينا 22، خط أفقي صلب، 210، 198، خط أفقي صلب، 120، 110، خط أفقي، 100، 88، خط أفقي صلب، 120، 110، خط أفقي صلب، 100، 88، خط أفقي صلب، ثم ثلاث نقاط. يشار إلى أن 120 يتكرر وأن 100 يتكرر. يتم شرح هذا أيضًا على أنه «يتكرر النمط، لذلك ستتكرر الأرقام في حاصل القسمة أيضًا. في النهاية، نحصل على عبارة مفادها أن 43/22 يساوي 1.954 بخط أفقي صغير فوق 54.$

التمارين $\PageIndex{41}$

اكتب $\dfrac{27}{11}$ في صورة عدد عشري.

إجابة: $2.\overline{45}$

التمارين $\PageIndex{42}$

اكتب $\dfrac{51}{22}$ في صورة عدد عشري.

إجابة: $2.3\overline{18}$

في بعض الأحيان قد نضطر إلى تبسيط التعبيرات بالكسور والأرقام العشرية معًا.

التمارين $\PageIndex{43}$

قم بالتبسيط: $\dfrac{7}{8}+6.4$ .

إجابة

يجب علينا أولاً تغيير رقم واحد بحيث يكون كلا الرقمين في نفس الشكل. يمكننا تغيير الكسر إلى رقم عشري، أو تغيير الرقم العشري إلى كسر. عادة ما يكون من الأسهل تغيير الكسر إلى رقم عشري.

		$\dfrac{7}{8}+6.4$
قم بالتغيير $\dfrac{7}{8}$ إلى رقم عشري.	$.$
أضف.		$0.875+6.4$
		$7.275$
		لذا، $\dfrac{7}{8}+6.4 = 7.275$

التمارين $\PageIndex{44}$

قم بالتبسيط: $\dfrac{3}{8}+4.9$ .

إجابة: $5.275$

التمارين $\PageIndex{45}$

قم بالتبسيط: $5.7 + \dfrac{13}{20}$ .

إجابة: $6.35$

النسبة المئوية هي نسبة مقامها 100. النسبة المئوية تعني لكل مائة. نحن نستخدم رمز النسبة المئوية،%، لإظهار النسبة المئوية.

بالمائة

النسبة المئوية هي نسبة مقامها 100.

نظرًا لأن النسبة المئوية هي نسبة، يمكن التعبير عنها بسهولة في صورة كسر. النسبة المئوية تعني لكل 100، وبالتالي فإن مقام الكسر هو 100. ثم نغير الكسر إلى رقم عشري بقسمة البسط على المقام.

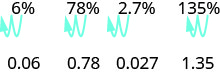
$\begin{array} {llll} {} &{\text{6%}} &{\text{78%}} &{\text{135%}} \\ {\text { Write as a ratio with denominator } 100. } &{\dfrac{6}{100}} &{\dfrac{78}{100}} &{\dfrac{135}{100}} \\ { \text { Change the fraction to a decimal by dividing}} &{0.06} &{0.78} &{1.35}\\ {\text{the numerator by the denominator.}} &{} &{} &{} \end{array}$

هل ترى النمط؟ لتحويل رقم النسبة المئوية إلى رقم عشري، ننقل العلامة العشرية مكانين إلى اليسار.

يُظهر الجزء الأول من هذا الشكل 6% بسهم مرسوم من بين 6 وعلامة النسبة المئوية إلى المسافة الموجودة على يسار 6 ثم إلى المسافة البعيدة إلى يسار تلك المساحة. تحت هذا، يتم إعطاء الرقم 0.06. يُظهر الجزء الثاني من هذا الشكل 78٪ بسهم مرسوم من بين 8 وعلامة النسبة المئوية إلى المسافة بين 7 و 8 ثم إلى المسافة الموجودة على يسار 7. تحت هذا، يتم إعطاء الرقم 0.78. يُظهر الجزء الثالث من هذا الشكل 2.7% بسهم مرسوم من النقطة العشرية إلى المسافة إلى يسار 2 ثم إلى المسافة البعيدة إلى يسار تلك المساحة. تحت هذا، يتم إعطاء الرقم 0.027. يُظهر الجزء الرابع من هذا الشكل 135% بسهم مرسوم من بين 5 وعلامة النسبة المئوية إلى المسافة بين 3 و5 ثم إلى المسافة بين 1 و3. تحت هذا، يتم إعطاء الرقم 1.35. — الشكل $\PageIndex{2}$

التمارين $\PageIndex{46}$

قم بتحويل كل نسبة مئوية إلى عدد عشري:

62%
135%
35.7 في المائة.

إجابة

1.
	$.$
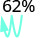
انقل العلامة العشرية مكانين إلى اليسار.	0.62

2.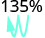
	$.$
انقل العلامة العشرية مكانين إلى اليسار.	1.35

3.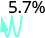
	$.$
انقل العلامة العشرية مكانين إلى اليسار.	0.057

التمارين $\PageIndex{47}$

قم بتحويل كل نسبة مئوية إلى عدد عشري:

9%
87%
3.9%.

إجابة

0.09
0.87
0.039

التمارين $\PageIndex{48}$

قم بتحويل كل نسبة مئوية إلى عدد عشري:

3%
91%
8.3%.

إجابة

0.03
0.91
0.083

إن تحويل عدد عشري إلى نسبة مئوية أمر منطقي إذا تذكرنا تعريف النسبة المئوية ووضعنا القيمة المكانية في الاعتبار.

لتحويل عدد عشري إلى نسبة مئوية، تذكر أن النسبة المئوية تعني لكل مائة. إذا غيرنا العدد العشري إلى كسر مقامه 100، فمن السهل تغيير هذا الكسر إلى نسبة مئوية.

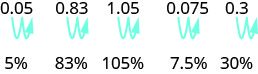
$\begin{array} {llll} {} &{0.83} &{1.05} &{0.075} \\ {\text {Write as a fraction }} &{\frac{83}{100}} &{\small{1}\frac{5}{100}} &{\frac{75}{1000}} \\ { \text {The denominator is 100.}} &{} &{\frac{105}{100}} &{\frac{7.5}{100}}\\ {\text{Write the ratio as a percent.}} &{\text{83%}} &{\text{105%}} &{\text{7.5%}} \end{array}$

التعرف على النمط؟ لتحويل عدد عشري إلى نسبة مئوية، ننقل العلامة العشرية إلى منزلتين إلى اليمين ثم نضيف علامة النسبة المئوية.

يُظهر الجزء الأول من هذا الشكل 0.05 بسهم مرسوم من النقطة العشرية إلى المسافة بين 0 و5 ثم إلى المسافة بعد 5. تحت هذا، يتم إعطاء الرقم 5٪. يُظهر الجزء الثاني من هذا الشكل 0.83 بسهم مرسوم من النقطة العشرية إلى المسافة بين 8 و3 ثم إلى المسافة بعد 3. تحت هذا، يتم إعطاء الرقم 83٪. يُظهر الجزء الثالث من هذا الشكل 1.05 بسهم مرسوم من النقطة العشرية إلى المسافة بين 0 و5 ثم إلى المسافة بعد 5. تحت هذا، يتم إعطاء الرقم 105٪. يُظهر الجزء الرابع من هذا الشكل 0.075 بسهم مرسوم من النقطة العشرية إلى المسافة بين 0 و7 ثم إلى المسافة بين 7 و5. تحت هذا، يتم إعطاء الرقم 7.5٪. يُظهر الجزء الخامس من هذا الشكل 0.3 بسهم مرسوم من النقطة العشرية إلى المسافة بعد 3 ثم المسافة إلى أقصى يمين ذلك الرقم 3. تحت هذا، يتم إعطاء الرقم 30٪. — الشكل $\PageIndex{3}$

التمارين $\PageIndex{49}$

قم بتحويل كل عدد عشري إلى نسبة مئوية:

0.51
1.25
0.093.

إجابة

1.
	$.$
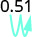
انقل العلامة العشرية مكانين إلى اليمين.	$51%$

2.
	$.$
انقل العلامة العشرية مكانين إلى اليمين.	$125%$

3.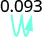
	$.$
انقل العلامة العشرية مكانين إلى اليمين.	$9.3%$

التمارين $\PageIndex{50}$

قم بتحويل كل عدد عشري إلى نسبة مئوية:

0.17
1.75
0.0825

إجابة

17%
175%
8.25%

التمارين $\PageIndex{51}$

قم بتحويل كل عدد عشري إلى نسبة مئوية:

0.41
2.25
0.0925.

إجابة

41%
225 في المائة
9.25%

المفاهيم الرئيسية

قم بتسمية عدد عشري
1. قم بتسمية الرقم على يسار الفاصلة العشرية.
2. اكتب «و» للفاصلة العشرية.
3. قم بتسمية جزء «الرقم» على يمين العلامة العشرية كما لو كان رقمًا صحيحًا.
4. قم بتسمية المكان العشري للرقم الأخير.
اكتب عددًا عشريًا
1. ابحث عن الكلمة «و» - فهي تحدد العلامة العشرية. ضع علامة عشرية تحت الكلمة «و». قم بترجمة الكلمات قبل 'و' إلى الرقم الصحيح ووضعها على يسار الفاصلة العشرية. إذا لم يكن هناك «و»، فاكتب «0" بنقطة عشرية على يمينها.
2. حدد عدد المنازل العشرية المطلوبة على يمين الفاصلة العشرية من خلال ملاحظة القيمة المكانية المشار إليها بالكلمة الأخيرة.
3. ترجم الكلمات بعد 'و' إلى الرقم الموجود على يمين الفاصلة العشرية. اكتب الرقم في المسافات - ضع الرقم النهائي في المكان الأخير.
4. املأ الأصفار لحوامل الأماكن حسب الحاجة.
تقريب عدد عشري
1. حدد القيمة المكانية المحددة وقم بتمييزها بسهم.
2. ضع خط تحت الرقم الموجود على يمين القيمة المكانية.
3. هل هذا الرقم أكبر من أو يساوي 5؟ نعم - أضف 1 إلى الرقم في القيمة المكانية المحددة. لا - لا تقم بتغيير الرقم في القيمة المكانية المحددة.
4. أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب.
جمع الأعداد العشرية أو طرحها
1. اكتب الأرقام بحيث تصطف النقاط العشرية رأسيًا.
2. استخدم الأصفار كحوامل، حسب الحاجة.
3. قم بإضافة الأرقام أو طرحها كما لو كانت أرقامًا صحيحة. ثم ضع الرقم العشري في الإجابة تحت النقاط العشرية في الأرقام المعطاة.
ضرب الأعداد العشرية
1. حدد علامة المنتج.
2. اكتب في شكل عمودي، واصطف الأرقام على اليمين. اضرب الأرقام كما لو كانت أرقامًا كاملة، مع تجاهل النقاط العشرية مؤقتًا.
3. ضع النقطة العشرية. عدد المنازل العشرية في المنتج هو مجموع المنازل العشرية في العوامل.
4. اكتب المنتج بالعلامة المناسبة.
ضرب عدد عشري في قوة العدد عشرة
1. انقل النقطة العشرية إلى اليمين بنفس عدد الأماكن مثل عدد الأصفار بقوة 10.
2. أضف الأصفار في نهاية الرقم حسب الحاجة.
قسمة الأعداد العشرية
1. حدد علامة حاصل القسمة.
2. اجعل المقسوم رقمًا صحيحًا عن طريق «نقل» العلامة العشرية إلى اليمين. «انقل» النقطة العشرية في التوزيعات بنفس عدد الأماكن - بإضافة الأصفار حسب الحاجة.
3. يقسم. ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات.
4. اكتب حاصل القسمة مع العلامة المناسبة.
تحويل عدد عشري إلى كسر صحيح
1. حدد القيمة المكانية للرقم النهائي.
2. اكتب الكسر: البسط - «الأرقام» على يمين العلامة العشرية؛ القاسم - القيمة المكانية المقابلة للرقم النهائي.
حوِّل الكسر إلى العدد العشري اقسم بسط الكسر على المقام.

أهداف التعلم

ملاحظة

اسم الأعداد العشرية وكتابتها

التمارين1.8.1\PageIndex{1}

التمارين1.8.2\PageIndex{2}

التمارين1.8.3\PageIndex{3}

قم بتسمية رقم عشري.

التمارين1.8.4\PageIndex{4}

التمارين1.8.5\PageIndex{5}

التمارين1.8.6\PageIndex{6}

التمارين1.8.7\PageIndex{7}: How to Write decimals

التمارين1.8.8\PageIndex{8}

التمارين1.8.9\PageIndex{9}

اكتب عددًا عشريًا.

الأعداد العشرية المستديرة

التمارين1.8.10\PageIndex{10}

التمارين1.8.11\PageIndex{11}

التمارين1.8.12\PageIndex{12}

الأرقام العشرية المستديرة.

التمارين1.8.13\PageIndex{13}

التمارين1.8.14\PageIndex{14}

التمارين1.8.15\PageIndex{15}

جمع الأعداد العشرية وطرحها

قم بإضافة أو طرح الأرقام العشرية.

التمارين1.8.16\PageIndex{16}

التمارين1.8.17\PageIndex{17}

التمارين1.8.18\PageIndex{18}

التمارين1.8.19\PageIndex{19}

التمارين1.8.20\PageIndex{20}

التمارين1.8.21\PageIndex{21}

ضرب الأعداد العشرية وقسمتها

ضرب الأعداد العشرية.

التمارين1.8.22\PageIndex{22}

التمارين1.8.23\PageIndex{23}

التمارين1.8.24\PageIndex{24}

اضرب عددًا عشريًا في قوة عشرة.

التمارين1.8.25\PageIndex{25}

التمارين1.8.26\PageIndex{26}

التمارين1.8.27\PageIndex{27}

قسمة الأرقام العشرية.

التمارين1.8.28\PageIndex{28}

التمارين1.8.29\PageIndex{29}

التمارين1.8.30\PageIndex{30}

التمارين1.8.31\PageIndex{31}

التمارين1.8.32\PageIndex{32}

التمارين1.8.33\PageIndex{33}

تحويل الأعداد العشرية والكسور والنسب المئوية

قم بتحويل عدد عشري إلى كسر مناسب.

التمارين1.8.34\PageIndex{34}

التمارين1.8.35\PageIndex{35}

التمارين1.8.36\PageIndex{36}

قم بتحويل كسر إلى رقم عشري.

التمارين1.8.37\PageIndex{37}

التمارين1.8.38\PageIndex{38}

التمارين1.8.39\PageIndex{39}

تكرار العدد العشري

التمارين1.8.40\PageIndex{40}

التمارين1.8.41\PageIndex{41}

التمارين1.8.42\PageIndex{42}

التمارين1.8.43\PageIndex{43}

التمارين1.8.44\PageIndex{44}

التمارين1.8.45\PageIndex{45}

بالمائة

التمارين1.8.46\PageIndex{46}

التمارين1.8.47\PageIndex{47}

التمارين1.8.48\PageIndex{48}

التمارين1.8.49\PageIndex{49}

التمارين1.8.50\PageIndex{50}

التمارين1.8.51\PageIndex{51}

المفاهيم الرئيسية

التمارين $\PageIndex{1}$

التمارين $\PageIndex{2}$

التمارين $\PageIndex{3}$

التمارين $\PageIndex{4}$

التمارين $\PageIndex{5}$

التمارين $\PageIndex{6}$

التمارين $\PageIndex{7}$ : How to Write decimals

التمارين $\PageIndex{8}$

التمارين $\PageIndex{9}$

التمارين $\PageIndex{10}$

التمارين $\PageIndex{11}$

التمارين $\PageIndex{12}$

التمارين $\PageIndex{13}$

التمارين $\PageIndex{14}$

التمارين $\PageIndex{15}$

التمارين $\PageIndex{16}$

التمارين $\PageIndex{17}$

التمارين $\PageIndex{18}$

التمارين $\PageIndex{19}$

التمارين $\PageIndex{20}$

التمارين $\PageIndex{21}$

التمارين $\PageIndex{22}$

التمارين $\PageIndex{23}$

التمارين $\PageIndex{24}$

التمارين $\PageIndex{25}$

التمارين $\PageIndex{26}$

التمارين $\PageIndex{27}$

التمارين $\PageIndex{28}$

التمارين $\PageIndex{29}$

التمارين $\PageIndex{30}$

التمارين $\PageIndex{31}$

التمارين $\PageIndex{32}$

التمارين $\PageIndex{33}$

التمارين $\PageIndex{34}$

التمارين $\PageIndex{35}$

التمارين $\PageIndex{36}$

التمارين $\PageIndex{37}$

التمارين $\PageIndex{38}$

التمارين $\PageIndex{39}$

التمارين $\PageIndex{40}$

التمارين $\PageIndex{41}$

التمارين $\PageIndex{42}$

التمارين $\PageIndex{43}$

التمارين $\PageIndex{44}$

التمارين $\PageIndex{45}$

التمارين $\PageIndex{46}$

التمارين $\PageIndex{47}$

التمارين $\PageIndex{48}$

التمارين $\PageIndex{49}$

التمارين $\PageIndex{50}$

التمارين $\PageIndex{51}$