5.2: التوزيع الموحد
- Page ID
- 198942
التوزيع الموحد هو توزيع احتمالي مستمر ويهتم بالأحداث التي من المحتمل حدوثها بنفس القدر. عند حل المشكلات ذات التوزيع الموحد، احرص على ملاحظة ما إذا كانت البيانات شاملة أو حصرية لنقاط النهاية.
البيان الرياضي للتوزيع الموحد هو
\(f(x) = \frac{1}{b-a}\)من أجل\(a \leq x \leq b\)
حيث تكون\(a =\) أدنى قيمة\(x\) وأعلى\(b =\) قيمة لـ\(x\).
صيغ المتوسط النظري والانحراف المعياري هي
\(\mu=\frac{a+b}{2}\)و\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}\)
التمارين\(\PageIndex{1}\)
البيانات التالية هي عدد الركاب على 35 قارب صيد مستأجر مختلف. متوسط العينة = 7.9 والانحراف المعياري للعينة = 4.33. تتبع البيانات توزيعًا موحدًا حيث تكون جميع القيم بين الصفر و 14 بما في ذلك متساوية. اذكر قيم\(a\) و\(b\). اكتب التوزيع بالتدوين الصحيح، واحسب المتوسط النظري والانحراف المعياري.
\ (\ فهرس الصفحات {1}\) «>| 1 | 12 | 4 | 10 | 4 | 14 | 11 |
| 7 | 11 | 4 | 13 | 2 | 4 | 6 |
| 3 | 10 | 0 | 12 | 6 | 9 | 10 |
| 5 | 13 | 4 | 10 | 14 | 12 | 11 |
| 6 | 10 | 11 | 0 | 11 | 13 | 2 |
-
الجدول 5.1
مثال\(\PageIndex{2}\)
يتم توزيع مقدار الوقت، بالدقائق، الذي يجب أن ينتظره الشخص للحافلة بشكل موحد بين صفر و 15 دقيقة، بما في ذلك.
أ- ما احتمال انتظار الشخص لأقل من 12.5 دقيقة؟
- إجابة
-
a. let\(X\) = عدد الدقائق التي يجب أن ينتظرها الشخص للحافلة. \(a = 0\)و\(b = 15\). \(X \sim U(0, 15)\). اكتب دالة الكثافة الاحتمالية. \(f(x) = \frac{1}{15-0}=\frac{1}{15}\)من أجل\(0 \leq x \leq 15\).
ابحث\(P(x < 12.5)\). ارسم رسمًا بيانيًا.
\[P(x<k)=\text { (base) (height) }=(12.5-0)\left(\frac{1}{15}\right)=0.8333\nonumber\]
احتمال انتظار الشخص أقل من 12.5 دقيقة هو 0.8333.
الشكل 5.11
ب- في المتوسط، كم من الوقت يجب أن ينتظر الشخص؟ أوجد المتوسط\(\mu\) والانحراف المعياري\(\sigma\).
- إجابة
-
ب\(\mu=\frac{a+b}{2}=\frac{15+0}{2}=7.5\). في المتوسط، يجب على الشخص الانتظار 7.5 دقيقة.
\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}=\sqrt{\frac{(15-\theta)^{2}}{12}}=4.3\). الانحراف المعياري هو 4.3 دقيقة.
ج- تسعون بالمائة من الوقت، يقل الوقت الذي يجب أن ينتظره الشخص عن أي قيمة؟
ملاحظة
هذا يتطلب النسبة المئوية 90.
- إجابة
-
(ج) أوجد النسبة المئوية 90. ارسم رسمًا بيانيًا. دعونا\(k =\) 90 في المئة.
\ (P (x
\(0.90=(k)\left(\frac{1}{15}\right)\)
\(k=(0.90)(15)=13.5\)
)<k) > النسبة المئوية 90 هي 13.5 دقيقة. تسعين بالمائة من الوقت، يجب على الشخص الانتظار 13.5 دقيقة على الأكثر.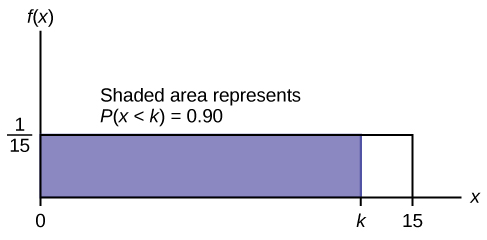 الشكل\(\PageIndex{12}\)
الشكل\(\PageIndex{12}\)
التمارين\(\PageIndex{2}\)
يتم توزيع المدة الإجمالية لألعاب البيسبول في الدوري الرئيسي في موسم 2011 بشكل موحد بين 447 ساعة و 521 ساعة.
- ابحث\(a\)\(b\) عن ما يمثلونه ووصفه.
- اكتب التوزيع.
- ابحث عن المتوسط والانحراف المعياري.
- ما احتمال أن تتراوح مدة مباريات الفريق لموسم 2011 بين 480 و500 ساعة؟


