12.5: نظرية ذات الحدين
- Page ID
- 201411
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم مثلث باسكال لتوسيع المعادلة ذات الحدين
- قم بتقييم المعامل ذي الحدين
- استخدم نظرية ذات الحدين لتوسيع معادلة ذات حدين
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بالتبسيط:\(\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}\).
إذا فاتتك هذه المشكلة، راجع مثال 1.25. - قم بتوسيع:\((3 x+5)^{2}\).
إذا فاتتك هذه المشكلة، راجع مثال 5.32. - قم بتوسيع:\((x-y)^{2}\).
إذا فاتتك هذه المشكلة، راجع مثال 5.32.
استخدم مثلث باسكال لتوسيع المعادلة ذات الحدين
في عملنا السابق، قمنا بتجميع المربعات ذات الحدين إما باستخدام FOIL أو باستخدام نمط المربعات ذات الحدين. يمكننا أيضًا القول أننا توسعنا\((a+b)^{2}\).
\((a+b)^{2}=a^{2}+2 a b+b^{2}\)
للتوسع\((a+b)^{3}\)، ندرك أن هذا يحدث\((a+b)^{2}(a+b)\) ويتضاعف.
\((a+b)^{3}\)
\((a+b)^{2}(a+b)\)
\(\left(a^{2}+2 a b+b^{2}\right)(a+b)\)
\(a^{3}+2 a^{2} b+a b^{2}+a^{2} b+2 a b^{2}+b^{3}\)
\(a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
\((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
للعثور على طريقة أقل تعقيدًا من شأنها أن تعمل مع التوسعات العالية مثل\((a+b)^{7}\)، نبحث مرة أخرى عن الأنماط في بعض التوسعات.
| عدد المصطلحات | الفصل الدراسي الأول | الفصل الدراسي الأخير | |
|---|---|---|---|
| \((a+b)^{1}=a+b\) | \(2\) | \(a^{1}\) | \(b^{1}\) |
| \((a+b)^{2}=a^{2}+2 a b+b^{2}\) | \(3\) | \(a^{2}\) | \(b^{2}\) |
| \((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\) | \(4\) | \(a^{3}\) | \(b^{3}\) |
| \((a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}\) | \(5\) | \(a^{4}\) | \(b^{4}\) |
| \((a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}\) | \(6\) | \(a^{5}\) | \(b^{5}\) |
| \((a+b)^{n}\) | \(n\) | \(a^{n}\) | \(b^{n}\) |
لاحظ أن المصطلحين الأول والأخير يعرضان متغيرًا واحدًا فقط. تذكر ذلك\(a^{0}=1\)، حتى نتمكن من إعادة كتابة المصطلحين الأول والأخير لتضمين كلا المتغيرين. على سبيل المثال، يمكننا التوسع\((a+b)^{3}\) لإظهار كل مصطلح مع كلا المتغيرين.
بشكل عام، لا نعرض الأسس الصفرية، تمامًا كما نكتب عادةً\(x\) بدلاً من\(1x\).
الأنماط في التوسع\((a+b)^{n}\)
- عدد المصطلحات هو\(n+1\).
- المصطلح الأول هو\(a^{n}\) والفصل الأخير هو\(b^{n}\).
- \(a\)تنخفض الأسس بمقدار واحد في كل فصل من اليسار إلى اليمين.
- \(b\)تزداد الأسس بمقدار واحد في كل فصل من اليسار إلى اليمين.
- مجموع الأسس في أي مصطلح هو\(n\).
لنلقِ نظرة على مثال لتسليط الضوء على الأنماط الثلاثة الأخيرة.
من الأنماط التي حددناها، نرى المتغيرات في التوسع\((a+b)^{n}\)، ستكون
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}\).
للعثور على معاملات المصطلحات، نكتب توسعاتنا مرة أخرى مع التركيز على المعاملات. نعيد كتابة المعاملات إلى اليمين لتشكيل مجموعة من المعاملات.
المصفوفة الموجودة على اليمين تسمى مثلث باسكال. لاحظ أن كل رقم في المصفوفة هو مجموع أقرب رقمين في الصف أعلاه. يمكننا العثور على الصف التالي من خلال البدء والانتهاء بواحد ثم إضافة رقمين متجاورين.
يعطي هذا المثلث معاملات المصطلحات عندما نقوم بتوسيع المقادير ذات الحدين.
مثلث باسكال
في المثال التالي، سنستخدم هذا المثلث والأنماط التي عرفناها لتوسيع المعادلة ذات الحدين.
استخدم مثلث باسكال للتوسيع\((x+y)^{6}\).
الحل:
نحن نعلم أن متغيرات هذا التوسع ستتبع النمط الذي حددناه. تبدأ الأسس غير الصفرية\(x\) لـ 6 وتنخفض إلى واحد. تبدأ الأسس غير الصفرية لـ\(y\) 1 وتزيد إلى ستة. سيكون مجموع الأسس في كل فصل ستة. في نمطنا،\(a=x\) و\(b=y\).
\(\begin{array}{l}{(a+b)^{n}=a^{n}+\_\_\_a^{n-1} b^{1}+\_\_\_a^{n-2} b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}} \\ {(x+y)^{6}=x^{6}+\_\_\_x^{5} y^{1}+\_\_\_x^{4} y^{2}+\_\_\_x^{3} y^{3}+\_\_\_x^{2} y^{4}+\_\_\_x^{1} y^{5}+y^{6}}\end{array}\)
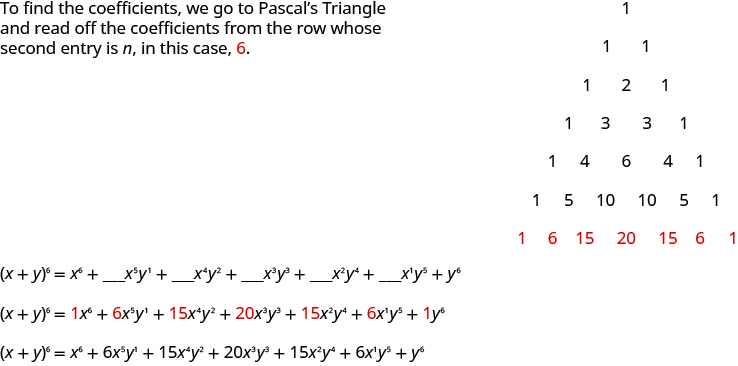
استخدم مثلث باسكال للتوسيع\((x+y)^{5}\).
- إجابة
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
استخدم مثلث باسكال للتوسيع\((p+q)^{7}\).
- إجابة
-
\(\begin{array}{c}{p^{7}+7 p^{6} q+21 p^{5} q^{2}+35 p^{4} q^{3}} {+35 p^{3} q^{4}+21 p^{2} q^{5}+7 p q^{6}+q^{7}}\end{array}\)
في المثال التالي، نريد توسيع المعادلة ذات الحدين بمتغير واحد وثابت واحد. نحن بحاجة إلى\(a\) تحديد النمط وتطبيقه بعناية.\(b\)
استخدم مثلث باسكال للتوسيع\((x+3)^{5}\).
الحل:
نحدد حرف\(a\)\(b\) و النمط.
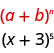
في نمطنا،\(a=x\) و\(b=3\).
نحن نعلم أن متغيرات هذا التوسع ستتبع النمط الذي حددناه. سيكون مجموع الأسس في كل فصل خمسة.
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((x+3)^{5}=x^{5}+\_\_\_x^{4}\cdot3^{1}+\_\_\_x^{3}\cdot3^{2}+\_\_\_x^{2}\cdot3^{3}+\_\_\_x^{1}\cdot3^{4}+3^{5}\)

استخدم مثلث باسكال للتوسيع\((x+2)^{4}\).
- إجابة
-
\(x^{4}+8 x^{3}+24 x^{2}+32 x+16\)
استخدم مثلث باسكال للتوسيع\((x+1)^{6}\).
- إجابة
-
\(\begin{array}{l}{x^{6}+6 x^{5}+15 x^{4}+20 x^{3}+15 x^{2}} {+6 x+1}\end{array}\)
في المثال التالي، يمثل الحدان فرقًا والحد الأول له ثابت مضروبًا في المتغير. بمجرد تحديد نموذج النموذج، يجب علينا مرة أخرى تطبيق النمط بعناية.\(a\)\(b\)
استخدم مثلث باسكال للتوسيع\((3x-2)^{4}\).
الحل:
نحدد حرف\(a\)\(b\) و النمط.
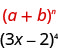
في نمطنا،\(a=3x\) و\(b=-2\).

\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((3 x-2 )^{4}=1 \cdot\left(\stackrel{3}{x}+4(3 x)^{3}(-2)^{1}+6(3 x)^{2}(-2)^{2}+4(3 x)^{1}(-2)^{3}+1 \cdot(-2)^{4}\right.\)
\((3 x-2)^{4}=81 x^{4}+4\left(27 x^{3}\right)(-2)+6\left(9 x^{2}\right)(4)+4(3 x)(-8)+1 \cdot 16\)
\((3 x-2 )^{4}=81 x^{4}-216 x^{3}+216 x^{2}-96 x+16\)
استخدم مثلث باسكال للتوسيع\((2x-3)^{4}\).
- إجابة
-
\(16 x^{4}-96 x^{3}+216 x^{2}-216 x+81\)
استخدم مثلث باسكال للتوسيع\((2x-1)^{6}\).
- إجابة
-
\(\begin{array}{l}{64 x^{6}-192 x^{5}+240 x^{4}-160 x^{3}} {+60 x^{2}-12 x+1}\end{array}\)
إيجاد قيمة المعامل ذي الحدين
في حين أن مثلث باسكال هو إحدى طرق توسيع المعادلة ذات الحدين، سننظر أيضًا في طريقة أخرى. قبل أن نصل إلى ذلك، نحتاج إلى تقديم المزيد من الرموز العاملية. لا يتم استخدام هذا الترميز فقط لتوسيع الحدود الثنائية، ولكن أيضًا في دراسة واستخدام الاحتمال.
للعثور على معاملات مصطلحات ذات حدين موسعة، سنحتاج إلى أن نكون قادرين على تقييم الترميز\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) الذي يسمى المعامل ذي الحدين. نقرأ على\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) أنها «\(n\)اختيار\(r\)» أو «\(n\)تؤخذ\(r\) في كل مرة».
يُعرَّف المعامل ذو الحدين\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\)\(r\)، أين\(b\) توجد الأعداد الصحيحة مع\(0 \leq r \leq n\)، على أنه
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
نقرأ\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) كـ "\(n\)اختيار\(r\)" أو "\(n\)مأخوذ\(r\) في كل مرة».
تقييم:
- \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
- \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
الحل:
أ- سنستخدم تعريف المعامل ذي الحدين،
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
استخدم التعريف\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\)، أين\(n=5, r=1\).
\(\frac{5 !}{1 !(5-1) !}\)
قم بالتبسيط.
\(\frac{5 !}{1 !(4) !}\)
أعد الكتابة\(5!\) باسم\(5\cdot 4!\)
\(\frac{5 \cdot 4 !}{1 ! \cdot 4 !}\)
قم بالتبسيط من خلال إزالة العوامل المشتركة.
\(\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}\)
قم بالتبسيط.
\(5\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5\)
ب.\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
استخدم التعريف\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\)، أين\(n=7, r=7\).
\(\frac{7 !}{7 !(7-7) !}\)
قم بالتبسيط.
\(\frac{7 !}{7 !(0) !}\)
قم بالتبسيط. تذكر\(0!=1\).
\(1\)
\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1\)
ج.\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
استخدم التعريف\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\)، أين\(n=4, r=0\).
\(\frac{4 !}{0 !(4-0) !}\)
قم بالتبسيط.
\(\frac{4 !}{0 !(4) !}\)
قم بالتبسيط.
\(1\)
\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1\)
د.\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
استخدم التعريف\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\)، أين\(n=8, r=5\).
\(\frac{8 !}{5 !(8-5) !}\)
قم بالتبسيط.
\(\frac{8 !}{5 !(3) !}\)
أعد الكتابة\(8!\) باسم\(8\cdot 7\cdot 6\cdot 5!\) وأزل العوامل المشتركة.
\(\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1}\)
قم بالتبسيط.
\(56\)
\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56\)
قم بتقييم كل معامل ذي حدين:
- \(\left( \begin{array}{l}{6} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {8}\end{array}\right)\)
- \(\left( \begin{array}{l}{5} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {3}\end{array}\right)\)
- إجابة
-
- \(6\)
- \(1\)
- \(1\)
- \(35\)
قم بتقييم كل معامل ذي حدين:
- \(\left( \begin{array}{l}{2} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{11} \\ {11}\end{array}\right)\)
- \(\left( \begin{array}{l}{9} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{6} \\ {5}\end{array}\right)\)
- إجابة
-
- \(2\)
- \(1\)
- \(1\)
- \(6\)
في المثال السابق\((a)\)\((b)\)،\((c)\) أظهر بعض الخصائص الخاصة للمعاملات ذات الحدين.
خصائص المعاملات ذات الحدين
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
استخدم نظرية ذات الحدين لتوسيع معادلة ذات حدين
نحن الآن جاهزون لاستخدام الطريقة البديلة لتوسيع الحدود الثنائية. تستخدم نظرية ذات الحدين نفس النمط للمتغيرات، ولكنها تستخدم المعامل ذي الحدين لمعامل كل حد.
نظرية ذات الحدين
لأي أرقام\(a\) حقيقية\(b\) وعدد صحيح موجب\(n\)،
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
استخدم نظرية ذات الحدين للتوسيع\((p+q)^{4}\).
الحل:
نحدد حرف\(a\)\(b\) و النمط.
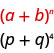
في نمطنا،\(a=p\) و\(b=q\).
نحن نستخدم نظرية ذات الحدين.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
استبدل القيم\(a=p, b=q\) و\(n=4\).
\((p+q)^{4}=\left( \begin{array}{c}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{4-1} q^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{4-2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p^{4-3} q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
قم بتبسيط الأسس.
\((p+q)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{3} q+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
قم بتقييم المعاملات، تذكر،\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((p+q)^{4}=1 p^{4}+4 p^{3} q^{1}+\frac{4 !}{2 !(2) !} p^{2} q^{2}+\frac{4 !}{3 !(4-3) !} p^{1} q^{3}+1 q^{4}\)
\((p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}\)
استخدم نظرية ذات الحدين للتوسيع\((x+y)^{5}\).
- إجابة
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
استخدم نظرية ذات الحدين للتوسيع\((m+n)^{6}\).
- إجابة
-
\(\begin{array}{l}{m^{6}+6 m^{5} n+15 m^{4} n^{2}+20 m^{3} n^{3}} {+15 m^{2} n^{4}+6 m n^{5}+n^{6}}\end{array}\)
لاحظ أنه عندما قمنا\((p+q)^{4}\) بالتوسع في المثال الأخير، باستخدام نظرية ذات الحدين، حصلنا على نفس المعاملات التي سنحصل عليها من استخدام مثلث باسكال.
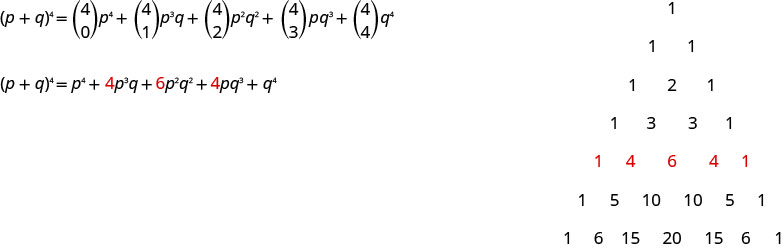
المثال التالي، المعادلة ذات الحدين هي الفرق. عندما يكون الحد ذو الحدين فرقًا، يجب أن نكون حذرين في تحديد القيم التي سنستخدمها في النمط.
استخدم نظرية ذات الحدين للتوسيع\((x-2)^{5}\).
الحل:
نحدد حرف\(a\)\(b\) و النمط.
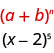
في نمطنا،\(a=x\) و\(b=-2\).
نحن نستخدم نظرية ذات الحدين.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
استبدل القيم\(a=x, b=-2\)، و\(n=5\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{5-1}(-2)^{1}+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{5-2}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{5-3}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x^{5-4}(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
قم بتبسيط المعاملات. تذكر،\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{4}(-2)+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{3}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{2}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
\((x-2)^{5}=1 x^{5}+5(-2) x^{4}+\frac{5 !}{2 ! \cdot 3 !}(-2)^{2} x^{3}+\frac{5 !}{3 ! 2 !}(-2)^{3} x^{2}+\frac{5 !}{4 !1 !}(-2)^{4} x+1(-2)^{5}\)
\((x-2)^{5}=x^{5}+5(-2) x^{4}+10 \cdot 4 \cdot x^{3}+10(-8) x^{2}+5 \cdot 16 \cdot x+1(-32)\)
\((x-2)^{5}=x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32\)
استخدم نظرية ذات الحدين للتوسيع\((x-3)^{5}\).
- إجابة
-
\(\begin{array}{l}{x^{5}-15 x^{4}+90 x^{3}-270 x^{2}} {+405 x-243}\end{array}\)
استخدم نظرية ذات الحدين للتوسيع\((y-1)^{6}\).
- إجابة
-
\(\begin{array}{l}{y^{6}-6 y^{5}+15 y^{4}-20 y^{3}+15 y^{2}} {-6 y+1}\end{array}\)
يمكن أن تصبح الأمور فوضوية عندما يحتوي كلا المصطلحين على معامل ومتغير.
استخدم نظرية ذات الحدين للتوسيع\((2x-3y)^{4}\).
الحل:
نحدد حرف\(a\)\(b\) و النمط.
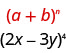
في نمطنا،\(a=2x\) و\(b=-3y\).
نحن نستخدم نظرية ذات الحدين.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
استبدل القيم\(a=2x, b=-3y\) و\(n=4\).
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{4-1}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{4-2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{4-3}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) (-3y)^{4}\)
قم بتبسيط الأسس.
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{3}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{1}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right)(-3 y)^{4}\)
قم بتقييم المعاملات. تذكر،\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((2 x-3 y)^{4}=1(2 x)^{4}+4(2 x)^{3}(-3 y)^{1}+\frac{4 !}{2 !(2 x) !}(2 x)^{2}+\frac{4 !}{3 !(4-3) !}(2 x)^{3}(-3 y)^{3}+1(-3 y)^{4}\)
\((2 x-3 y)^{4}=16 x^{4}+4 \cdot 8 x^{3}(-3 y)+6\left(4 x^{2}\right)\left(9 y^{2}\right)+4(2 x)\left(-27 y^{3}\right)+81 y^{4}\)
\((2 x-3 y)^{4}=16 x^{4}-96 x^{3} y+216 x^{2} y^{2}-216 x y^{3}+81 y^{4}\)
استخدم نظرية ذات الحدين للتوسيع\((3x-2y)^{5}\).
- إجابة
-
\(\begin{array}{l}{243 x^{5}-810 x^{4} y+1080 x^{3} y^{2}} {-720 x^{2} y^{3}+240 x y^{4}-32 y^{5}}\end{array}\)
استخدم نظرية ذات الحدين للتوسيع\((4x-3y)^{4}\).
- إجابة
-
\(\begin{array}{l}{256 x^{4}-768 x^{3} y+864 x^{2} y^{2}} {-432 x y^{3}+81 y^{4}}\end{array}\)
الجمال الحقيقي لنظرية ذات الحدين هو أنها تعطي صيغة لأي مصطلح معين من التوسع دون الحاجة إلى حساب المجموع الكلي. دعونا نبحث عن نمط في نظرية ذات الحدين.
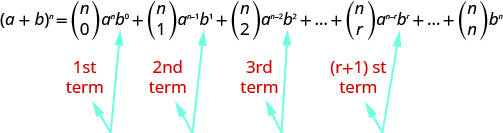
لاحظ أنه في كل حالة يكون الأس\(b\) الموجود على الحرف أقل بمقدار واحد من رقم المصطلح. \((r+1)^{st}\)المصطلح هو المصطلح الذي يكون فيه\(b\) الأس\(r\). لذلك يمكننا استخدام تنسيق\((r+1)^{st}\) المصطلح للعثور على قيمة مصطلح معين.
ابحث عن حد معين في التوسعة ذات الحدين
\((r+1)^{s t}\)المصطلح في التوسع\((a+b)^{n}\) هو
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}\)
ابحث عن الفصل الرابع من\((x+y)^{7}\).
الحل:
| في نمطنا،\(n=7, a=x\) و\(b=y\). | 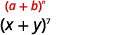 |
|
نحن نبحث عن الفصل الرابع. منذ\(r+1=4\) ذلك الحين\(r=3\). |
|
| اكتب الصيغة | 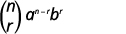 |
| استبدل القيم و\(n=7, r=3, a=x\) و\(b=y\). | 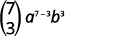 |
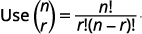 |
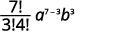 |
| قم بالتبسيط. | 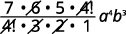 |
| قم بالتبسيط. |  |
ابحث عن الفصل الثالث من\((x+y)^{6}\).
- إجابة
-
\(15x^{4}y^{2}\)
ابحث عن الفصل الخامس من\((a+b)^{8}\).
- إجابة
-
\(8ab^{7}\)
أوجد معامل\(x^{6}\) مصطلح\((x+3)^{9}\).
الحل:
| في نمطنا، إذن\(n=9, a=x\)، و\(b=3\). |

|
| نحن نبحث عن معامل\(x^{6}\) المصطلح. منذ\(a=x\) ذلك الحين\(x^{9-r}=x^{6}\)، ونحن نعلم\(r=3\). | |
| اكتب الصيغة. |
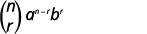
|
| استبدل القيم و\(n=9, 4=3, a=x\) و\(b=3\). |
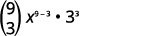
|
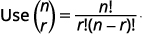
|
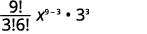
|
| قم بالتبسيط. |
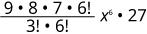
|
| قم بالتبسيط. |
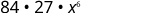
|
| قم بالتبسيط. |

|
أوجد معامل\(x^{5}\) مصطلح\((x+4)^{8}\).
- إجابة
-
\(7,168\)
أوجد معامل\(x^{4}\) مصطلح\((x+2)^{7}\).
- إجابة
-
\(280\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة باستخدام التسلسلات.
المفاهيم الرئيسية
- الأنماط في توسيع\ (a+b) ^ {n}\ (
- عدد المصطلحات هو\(n+1\).
- المصطلح الأول هو\(a^{n}\) والفصل الأخير هو\(b^{n}\).
- \(a\)تنخفض الأسس بمقدار واحد في كل فصل من اليسار إلى اليمين.
- \(b\)تزداد الأسس بمقدار واحد في كل فصل من اليسار إلى اليمين.
- مجموع الأسس في أي مصطلح هو\(n\).
- مثلث باسكال

- المعامل ذو الحدين \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\): يُعرَّف المعامل ذو الحدين\(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\)، حيث\(r\)\(n\) تكون الأعداد الصحيحة مع\(0≤r≤n\)، على أنه
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
نقرأ على\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) أنها «\(n\)اختيار\(r\)» أو «\(n\)تؤخذ\(r\) في كل مرة».
- خصائص المعاملات ذات الحدين
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
- نظرية ذات الحدين:
لأي أرقام حقيقية\(a\)\(b\)، وعدد صحيح موجب\(n\)،
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)


