12.4: المتتابعات الهندسية والمسلسلات
- Page ID
- 201386
في نهاية هذا القسم، ستكون قادرًا على:
- حدد ما إذا كان التسلسل هندسيًا
- ابحث عن الحد العام (الحد\(n\) العاشر) للتسلسل الهندسي
- أوجد مجموع الحدود\(n\) الأولى للتسلسل الهندسي
- أوجد مجموع متسلسلة هندسية لا نهائية
- قم بتطبيق التسلسلات الهندسية والمسلسلات في العالم الحقيقي
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بالتبسيط:\(\frac{24}{32}\).
إذا فاتتك هذه المشكلة، راجع المثال 1.24. - تقييم: أ.\(3^{4}\) ب\(\left(\frac{1}{2}\right)^{4}\).
إذا فاتتك هذه المشكلة، راجع المثال 1.19. - إذا\(f(x)=4 \cdot 3^{x}\)، ابحث عن أ.\(f(1)\) ب.\(f(2)\) ج\(f(3)\).
إذا فاتتك هذه المشكلة، راجع المثال 3.49.
حدد ما إذا كان التسلسل هندسيًا
نحن الآن جاهزون للنظر في النوع الخاص الثاني من التسلسل، التسلسل الهندسي.
يُطلق على التسلسل اسم التسلسل الهندسي إذا كانت النسبة بين المصطلحات المتتالية هي نفسها دائمًا. النسبة بين الحدود المتتالية في تسلسل هندسي هي\(r\)، النسبة الشائعة، حيث تكون\(n\) أكبر من أو تساوي اثنين.
التسلسل الهندسي هو تسلسل تكون فيه النسبة بين المصطلحات المتتالية هي نفسها دائمًا.
النسبة بين المصطلحات المتتالية\(\frac{a_{n}}{a_{n-1}}\)\(r\)، هي النسبة الشائعة. \(n\)أكبر من أو يساوي اثنين.
فكر في هذه التسلسلات.
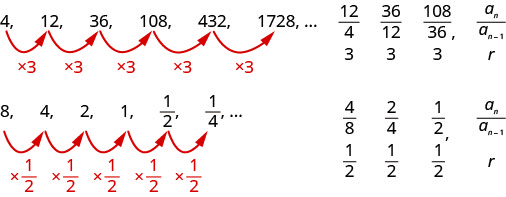
حدد ما إذا كان كل تسلسل هندسيًا. إذا كان الأمر كذلك، فحدد النسبة الشائعة.
- \(4,8,16,32,64,128, \dots\)
- \(-2,6,-12,36,-72,216, \dots\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
الحل:
لتحديد ما إذا كان التسلسل هندسيًا، نجد نسبة الحدود المتتالية الموضحة.
أ- ابحث عن نسبة المصطلحات المتتالية
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8}{4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{aligned}\)
التسلسل هندسي. الحصة الشائعة هي\(r=2\).
ب- ابحث عن نسبة المصطلحات المتتالية
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \:\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end{aligned}\)
التسلسل ليس هندسيًا. لا توجد نسبة مشتركة.
ج- ابحث عن نسبة المصطلحات المتتالية
\(\begin{aligned}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ldots\\ & \frac{9}{27}\quad\frac{3}{9}\quad\frac{1}{3}\quad\frac{\frac{1}{3}}{1}\quad\frac{\frac{1}{9}}{\frac{1}{3}}\\ &\frac{1}{3}\quad\;\:\frac{1}{3}\quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
التسلسل هندسي. النسبة الشائعة هي\(r=\frac{1}{3}\).
حدد ما إذا كان كل تسلسل هندسيًا. إذا كان الأمر كذلك، فحدد النسبة الشائعة.
- \(7,21,63,189,567,1,701, \dots\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1,440, \dots\)
- إجابة
-
- التسلسل هندسي بنسبة مشتركة\(r=3\).
- التسلسل هندسي بنسبة مشتركة\(d=\frac{1}{4}\).
- التسلسل ليس هندسيًا. لا توجد نسبة مشتركة.
حدد ما إذا كان كل تسلسل هندسيًا. إذا كان الأمر كذلك، فحدد النسبة الشائعة.
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \dots\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- إجابة
-
- التسلسل ليس هندسيًا. لا توجد نسبة مشتركة.
- التسلسل هندسي بنسبة مشتركة\(r=2\).
- التسلسل هندسي بنسبة مشتركة\(r=\frac{1}{2}\).
إذا عرفنا المصطلح الأول والنسبة المشتركة\(r\)، فيمكننا سرد عدد محدود من مصطلحات التسلسل.\(a_{1}\)
اكتب الحدود الخمسة الأولى من التسلسل حيث يكون\(3\) الحد الأول والنسبة المشتركة\(r=−2\).
الحل:
نبدأ بالمصطلح الأول ونضربه في النسبة المشتركة. ثم نضرب هذه النتيجة في النسبة المشتركة للحصول على المصطلح التالي، وهكذا.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3} & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{array}\)
الإجابة:
التسلسل هو\(3,-6,12,-24,48, \dots\)
اكتب الحدود الخمسة الأولى من التسلسل حيث يكون\(7\) الحد الأول والنسبة المشتركة\(r=−3\).
- إجابة
-
\(7,-21,63,-189,567\)
اكتب الحدود الخمسة الأولى من التسلسل حيث يكون\(6\) الحد الأول والنسبة المشتركة\(r=−4\).
- إجابة
-
\(6,-24,96,-384,1536\)
أوجد الحد العام (\(n\)الحد العاشر) للمتتابعة الهندسية
مثلما وجدنا صيغة للحد العام للتسلسل والمسلسل الحسابي، يمكننا أيضًا العثور على صيغة للمصطلح العام للتسلسل الهندسي.
لنكتب المصطلحات القليلة الأولى من التسلسل حيث يكون\(a_{1}\) المصطلح الأول والنسبة الشائعة\(r\). سنبحث بعد ذلك عن نمط.
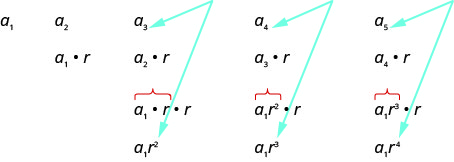
عندما نبحث عن نمط في المصطلحات الخمسة أعلاه، نرى أن كل مصطلح يبدأ بـ\(a_{1}\).
المصطلح الأول،\(a_{1}\)، لا يتم ضربه بأي مصطلح\(r\). في الفصل الثاني،\(a_{1}\) يتم ضرب الرقم بـ\(r\). في الفصل الثالث،\(a_{1}\) يتم ضرب الرقم\(r\) مرتين (\(r⋅r\)أو\(r^{2}\)). في الفصل الرابع،\(a_{1}\) يتم ضرب الرقم في\(r\) ثلاث مرات (\(r⋅r⋅r\)أو\(r^{3}\)) وفي الفصل الخامس،\(a_{1}\) يتم ضربه\(r\) بأربع مرات. في كل فصل،\(a_{1}\) يتم ضرب عدد المرات في أقل بمقدار\(r\) واحد من عدد المصطلح. هذا يقودنا إلى ما يلي
\(a_{n}=a_{1} r^{n-1}\)
المصطلح العام للتسلسل الهندسي مع الحد الأول والنسبة المشتركة\(r\) هو\(a_{1}\)
\(a_{n}=a_{1} r^{n-1}\)
سنستخدم هذه الصيغة في المثال التالي للعثور على المصطلح الرابع عشر من التسلسل.
ابحث عن الحد الرابع عشر من التسلسل الذي يكون فيه الحد\(64\) الأول والنسبة الشائعة\(r=\frac{1}{2}\).
الحل:
\(a_{n}=a_{1} r^{n-1}\)
للعثور على المصطلح الرابع عشر\(a_{14}\)، استخدم الصيغة مع\(a_{1}=64\) و\(r=\frac{1}{2}\).
\(a_{14}=64\left(\frac{1}{2}\right)^{14-1}\)
استبدل القيم.
\(a_{14}=64\left(\frac{1}{2}\right)^{13}\)
قم بالتبسيط.
\(a_{14}=\frac{1}{128}\)
ابحث عن الحد الثالث عشر من التسلسل حيث يكون\(81\) الحد الأول والنسبة الشائعة هي\(r=\frac{1}{3}\).
- إجابة
-
\(\frac{1}{6,561}\)
أوجد الحد الثاني عشر من المتتابعة التي يكون\(256\) فيها الحد الأول والنسبة الشائعة هي\(r=\frac{1}{4}\).
- إجابة
-
\(\frac{1}{16,384}\)
في بعض الأحيان لا نعرف النسبة المشتركة ويجب علينا استخدام المعلومات المقدمة للعثور عليها قبل أن نجد المصطلح المطلوب.
ابحث عن الحد الثاني عشر من التسلسل\(3, 6, 12, 24, 48, 96, …\) ابحث عن الحد العام للتسلسل.
الحل:
لإيجاد الحد الثاني عشر، نستخدم الصيغة\(a_{n}=a_{1} r^{n-1}\)، ولذلك نحتاج أولاً إلى تحديد\(a_{1}\) النسبة المشتركة\(r\).
الفصل الأول هو ثلاثة.
\(3,6,12,24,48,96, \dots\)
\(a_{1}=3\)
أوجد النسبة المشتركة.
\(\begin{array}{l}{\frac{6}{3} \quad \frac{12}{6} \quad \frac{24}{12} \quad \frac{48}{24} \quad \frac{96}{48}} \\ {2 \:\:\:\quad 2 \quad \:\:2 \quad\:\:\: 2 \:\:\quad \:2} \\ {\text { The common ratio is } r=2}\end{array}\)
للعثور على المصطلح الثاني عشر\(a_{12}\)، استخدم الصيغة مع\(a_{1}=3\) و\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
استبدل القيم.
\(a_{12}=3 \cdot 2^{12-1}\)
قم بالتبسيط.
\(a_{12}=3 \cdot 2^{11}\)
\(a_{12}=6,144\)
ابحث عن المصطلح العام. نحن نستخدم الصيغة مع\(a_{1}=3\) و\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
\(a_{n}=3(2)^{n-1}\)
ابحث عن الحد التاسع من التسلسل\(6, 18, 54, 162, 486, 1,458, … \) ثم ابحث عن المصطلح العام للتسلسل.
- إجابة
-
\(a_{9}=39,366 .\)المصطلح العام هو\(a_{n}=6(3)^{n-1}\).
ابحث عن الحد الحادي عشر من التسلسل\(7, 14, 28, 56, 112, 224, …\) ثم ابحث عن المصطلح العام للتسلسل.
- إجابة
-
\(a_{11}=7,168 .\)المصطلح العام هو\(a_{n}=7(2)^{n-1}\).
أوجد مجموع الحدود\(n\) الأولى للمتتابعة الهندسية
وجدنا مجموع التسلسلات العامة والتسلسل الحسابي. سنفعل الآن نفس الشيء مع التسلسلات الهندسية. يُكتب مجموع\(n\) المصطلحات الأولى للتسلسل الهندسي كـ\(S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\).\(S_{n}\) يمكننا كتابة هذا المجموع من خلال البدء بالحد الأول\(a_{1}\)، والاستمرار في الضرب\(r\) للحصول على الحد التالي على النحو التالي:
\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)
دعونا أيضًا نضرب كلا طرفي المعادلة في\(r\).
\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)
بعد ذلك، نطرح هذه المعادلات. سنرى أنه عندما نطرح، يتم طرح كل الحد الأول من المعادلة العليا والحد الأخير من المعادلة السفلية إلى الصفر.
\(\begin{aligned} S_{n}&= a_{1}+a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1} \\ r S_{n} &= a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1}+a_{1} r^{n}\\\hline S_{n}-r S_{n} &= a_{1} -a_{1}r^{n} \end{aligned}\)
نحن نأخذ كلا الجانبين في الاعتبار.
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)
للحصول على الصيغة الخاصة بـ\(S_{n}\)، قسّم كلا الجانبين على\((1-r)\).
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
مجموع\(n\) المصطلحات الأولى للتسلسل الهندسي هو\(S_{n}\)
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
أين\(a_{1}\) المصطلح الأول\(r\) وهي النسبة المشتركة، ولا\(r\) تساوي واحدة.
نطبق هذه الصيغة في المثال التالي حيث يتم إعطاء المصطلحات القليلة الأولى من التسلسل. لاحظ أن مجموع التسلسل الهندسي عادةً ما يصبح كبيرًا جدًا عندما تكون النسبة المشتركة أكبر من واحد.
أوجد مجموع الحدود\(20\) الأولى للتسلسل الهندسي\(7, 14, 28, 56, 112, 224, …\)
الحل:
للعثور على المبلغ، سنستخدم الصيغة\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). نحن نعلم\(a_{1}=7\)\(r=2\)، و\(n=20\)،
معرفة\(a_{1}=7, r=2\) صيغة المجموع واستخدامها.\(n=20\)
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
استبدل القيم.
\(S_{20}=\frac{7\left(1-2^{20}\right)}{1-2}\)
قم بالتبسيط.
\(S_{20}=7,340,025\)
أوجد مجموع الحدود\(20\) الأولى للتسلسل الهندسي\(3, 6, 12, 24, 48, 96, …\)
- إجابة
-
\(3,145,725\)
أوجد مجموع الحدود\(20\) الأولى للتسلسل الهندسي\(6, 18, 54, 162, 486, 1,458, …\)
- إجابة
-
\(10,460,353,200\)
في المثال التالي، يتم إعطاؤنا المجموع في تدوين التلخيص. في حين أن إضافة جميع المصطلحات قد تكون ممكنة، إلا أنه غالبًا ما يكون من الأسهل استخدام الصيغة للعثور على مجموع\(n\) المصطلحات الأولى.
لاستخدام الصيغة، نحتاج\(r\). يمكننا العثور عليها من خلال كتابة المصطلحات القليلة الأولى من التسلسل وإيجاد نسبتها. هناك خيار آخر يتمثل في إدراك أنه في تدوين التلخيص، يتم كتابة التسلسل في النموذج\(\sum_{i=1}^{k} a(r)^{i}\)، حيث\(r\) توجد النسبة الشائعة.
ابحث عن المبلغ:\(\sum_{i=1}^{15} 2(3)^{i}\).
الحل:
للعثور على المبلغ، سنستخدم الصيغة\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\) التي تتطلب\(a_{1}\) و\(r\). سنكتب بعض المصطلحات، حتى نتمكن من الحصول على المعلومات المطلوبة.
 |
|
| اكتب المصطلحات القليلة الأولى. | 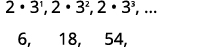 |
| تحديد\(a_{1}\). |  |
| أوجد النسبة المشتركة. |  |
| معرفة\(a_{1}=6\) صيغة المجموع واستخدامها.\(r=3\)\(n=15\) | 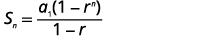 |
| استبدل القيم. | 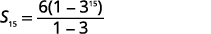 |
| قم بالتبسيط. | 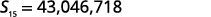 |
ابحث عن المبلغ:\(\sum_{i=1}^{15} 6(2)^{i}\).
- إجابة
-
\(393,204\)
ابحث عن المبلغ:\(\sum_{i=1}^{10} 5(2)^{i}\).
- إجابة
-
\(10,230\)
أوجد مجموع متسلسلة هندسية لا نهائية
إذا أخذنا تسلسلًا هندسيًا وقمنا بإضافة المصطلحات، فسيكون لدينا مجموع يسمى المتسلسلة الهندسية. المتسلسلة الهندسية اللانهائية هي مجموع لا نهائي يكون\(a_{1}\) الحد الأول والنسبة الشائعة مكتوبة.\(r\)
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
المتسلسلة الهندسية اللانهائية هي مجموع لا نهائي يكون\(a_{1}\) الحد الأول والنسبة الشائعة مكتوبة.\(r\)
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\dots\)
نحن نعرف كيفية إيجاد مجموع الحدود الأولى\(n\) من سلسلة هندسية باستخدام الصيغة،\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). ولكن كيف نجد مجموع مجموع لا نهائي؟
دعونا ننظر إلى السلسلة الهندسية اللانهائية\(3+6+12+24+48+96+….\). يصبح كل مصطلح أكبر وأكبر، لذا فمن المنطقي أن يصبح مجموع العدد اللانهائي من المصطلحات أكبر. دعونا نلقي نظرة على بعض المبالغ الجزئية لهذه السلسلة. نحن نرى\(a_{1}=3\) و\(r=2\)
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{3\left(1-2^{10}\right)}{1-2}} & {S_{30}=\frac{3\left(1-2^{30}\right)}{1-2}} & {S_{50}=\frac{3\left(1-2^{50}\right)}{1-2}} \\ {S_{10}=3,069} & {S_{30}=3,221,225,469} & {S_{50}\approx 3.38 \times 10^{15}}\end{array}\)
\(n\)كلما زاد حجمه وكبر، يصبح المجموع أكبر وأكبر. هذا صحيح عندما\(|r|≥1\) نسمي السلسلة متباينة. لا يمكننا العثور على مجموع سلسلة هندسية لا نهائية عندما\(|r|≥1\).
لنلقِ نظرة على سلسلة هندسية لا نهائية تكون نسبتها الشائعة أقل من جزء واحد
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots\). هنا تصبح المصطلحات أصغر وأصغر\(n\) كلما كبرت. دعونا نلقي نظرة على بعض المبالغ المحدودة لهذه السلسلة. نرى\(a_{1}=\frac{1}{2}\) و\(r=\frac{1}{2}\).
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{10}\right)}{1-\frac{1}{2}}} & {S_{20}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{20}\right)}{1-\frac{1}{2}}} & {S_{30}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{30}\right)}{1-\frac{1}{2}}} \\ {S_{10}\approx 0.9990234375} & {S_{20}\approx 0.9999990463} & {S_{30}\approx 0.9999999991}\end{array}\)
لاحظ أن المبلغ يصبح أكبر وأكبر ولكنه أيضًا يقترب أكثر فأكثر من واحد. عندما\(|r|<1\)\(r^{n}\) يصبح التعبير أصغر وأصغر. في هذه الحالة، نسمي السلسلة المتقاربة. مع\(n\) اقتراب اللانهاية، (تصبح كبيرة بشكل لا نهائي)،\(r^{n}\) تقترب أكثر فأكثر من الصفر. في صيغة المجموع الخاصة بنا، يمكننا\(r^{n}\) استبدال الصفر ثم نحصل على صيغة المجموع،\(S\)، لسلسلة هندسية لا نهائية عندما\(|r|<1\).
\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S &=\frac{a_{1}(1-0)}{1-r} \\ S &=\frac{a_{1}}{1-r} \end{aligned}\)
تعطينا هذه الصيغة مجموع التسلسل الهندسي اللانهائي. لاحظ أنه\(S\) لا يحتوي على النص المنخفض\(n\)\(S_{n}\) لأننا لا نضيف عددًا محدودًا من المصطلحات.
بالنسبة لسلسلة هندسية لا نهائية يكون\(a_{1}\) المصطلح الأول والنسبة الشائعة\(r\)،
إذا كان\(|r|<1\) المبلغ هو
\(S=\frac{a_{1}}{1-r}\)
إذا كانت\(|r|≥1\) السلسلة الهندسية اللانهائية لا تحتوي على مجموع. نقول أن السلسلة تتباعد.
أوجد مجموع المتسلسلة الهندسية اللانهائية\(54+18+6+2+\frac{2}{3}+\frac{2}{9}+\ldots\)
الحل:
للعثور على المجموع، علينا أولاً التحقق من النسبة المشتركة\(|r|<1\) ثم يمكننا استخدام صيغة المجموع\(S=\frac{a_{1}}{1-r}\).
أوجد النسبة المشتركة.
\(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{3}} & {r=\frac{1}{3} \quad|r|<1}\end{array}\)
تحديد\(a_{1}\).
\(a_{1}=54\)
مع العلم\(a_{1}=54, r=\frac{1}{3}\)، استخدم صيغة المجموع.
\(S=\frac{a_{1}}{1-r}\)
استبدل القيم.
\(S=\frac{54}{1-\frac{1}{3}}\)
قم بالتبسيط.
\(S=81\)
الإجابة:
\(S=80\)
أوجد مجموع المتسلسلة الهندسية اللانهائية\(48+24+12+6+3+\frac{3}{2}+\dots\)
- إجابة
-
\(96\)
أوجد مجموع المتسلسلة الهندسية اللانهائية\(64+16+4+1+\frac{1}{4}+\frac{1}{16}+\dots\)
- إجابة
-
\(\frac{256}{3}\)
استخدام مثير للاهتمام للمتسلسلات الهندسية اللانهائية هو كتابة عدد عشري متكرر في صورة كسر.
اكتب العدد العشري\(0.5\) المتكرر في صورة كسر.
الحل:
أعد كتابة\(0.5\) عرض الخمسة المتكررة. استخدم القيمة المكانية لإعادة كتابة هذا كمجموع. هذه سلسلة هندسية لا حصر لها.
0.555555555\(\ldots\)
\(0.5+0.05+0.005+0.0005+\dots\)
أوجد النسبة المشتركة.
\(\begin{array}{ll}{r=\frac{0.05}{0.5}} & {r=\frac{0.005}{0.05} \dots} \\ {r=0.1} & {r=0.1 \quad|r|<1}\end{array}\)
تحديد\(a_{1}\)
\(a_{1}=0.5\)
مع العلم\(a_{1}=0.5 ,r=0.1\)، استخدم صيغة المجموع.
\(S=\frac{a_{1}}{1-r}\)
استبدل القيم.
\(S=\frac{0.5}{1-0.1}\)
قم بالتبسيط.
\(S=\frac{0.5}{0.9}\)
اضرب البسط والمقام في\(10\).
\(S=\frac{5}{9}\)
يُطلب منا العثور على نموذج الكسر.
\(0.5 = \frac{5}{9}\)
اكتب العدد العشري\(0.4\) المتكرر في صورة كسر.
- إجابة
-
\(\frac{4}{9}\)
اكتب العدد العشري\(0.8\) المتكرر في صورة كسر.
- إجابة
-
\(\frac{8}{9}\)
قم بتطبيق المتتابعات الهندسية والمسلسلات في العالم الحقيقي
يتعلق أحد تطبيقات التسلسلات الهندسية بالإنفاق الاستهلاكي. إذا تم منح خصم ضريبي لكل أسرة، فإن التأثير على الاقتصاد هو عدة أضعاف مبلغ الخصم الفردي.
قررت الحكومة منح خصم\(1,000\) ضريبي بقيمة $ لكل أسرة من أجل تحفيز الاقتصاد. تشير الإحصاءات الحكومية إلى أن كل أسرة ستنفق\(80\)% من الخصم على السلع والخدمات. ستقوم الشركات والأفراد الذين استفادوا من هذه\(80\) النسبة المئوية بعد ذلك بإنفاق\(80\)% مما تلقوه وما إلى ذلك. النتيجة تسمى التأثير المضاعف. ما هو التأثير الكلي للخصم على الاقتصاد؟
الحل:
في كل مرة تذهب فيها الأموال إلى الاقتصاد، يتم إنفاق\(80\) النسبة المئوية منها ثم يتم إنفاقها في الاقتصاد. مرة أخرى، يتم إنفاق\(80\) النسبة المئوية من هذه الأموال في الاقتصاد مرة أخرى. يستمر هذا الوضع ويقودنا إلى سلسلة هندسية لا نهائية.
\(1000+1000(0.8)+1000(0.8)^{2}+\ldots\)
هنا المصطلح الأول هو\(1,000, a_{1}=1000\). النسبة الشائعة هي\(0.8, r=0.8\). يمكننا تقييم هذا المبلغ منذ ذلك الحين\(0.8<1\). نستخدم صيغة المجموع في سلسلة هندسية لا نهائية.
\(S=\frac{a_{1}}{1-r}\)
استبدل القيم،\(a_{1}=1,000\) و\(r=0.8\).
\(S=\frac{1,000}{1-0.8}\)
تقييم.
\(S=5,000\)
الإجابة:
سيكون التأثير الإجمالي للدولار الذي\(1,000\) تتلقاه كل أسرة هو\(5,000\) نمو الدولار في الاقتصاد.
ما هو التأثير الكلي على الاقتصاد للخصم الضريبي الحكومي بقيمة $\(1,000\) لكل أسرة من أجل تحفيز الاقتصاد إذا كانت كل أسرة ستنفق\(90\)٪ من الخصم على السلع والخدمات؟
- إجابة
-
$\(10,000\)
ما هو التأثير الكلي على الاقتصاد للخصم الضريبي الحكومي بقيمة $\(500\) لكل أسرة من أجل تحفيز الاقتصاد إذا كانت كل أسرة ستنفق\(85\)٪ من الخصم على السلع والخدمات؟
- إجابة
-
$\(3,333.33\)
لقد نظرنا إلى صيغة الفائدة المركبة حيث يتم استثمار رأس المال بسعر فائدة\(t\) لسنوات.\(P\)\(r\) الرصيد الجديد هو\(A=P\left(1+\frac{r}{n}\right)^{n t}\) عندما تتضاعف الفائدة\(n\) مرات في السنة.\(A\) تنطبق هذه الصيغة عندما يتم استثمار مبلغ مقطوع مقدمًا وتخبرنا بالقيمة بعد فترة زمنية معينة.
الأقساط السنوية هي استثمار عبارة عن سلسلة من الودائع الدورية المتساوية. سننظر في الأقساط السنوية التي تدفع الفائدة في وقت الإيداع. بينما نقوم بتطوير صيغة قيمة المعاش، سنسمح بذلك\(n=1\). هذا يعني أن هناك وديعة واحدة في السنة.
\(\begin{aligned} &A =P\left(1+\frac{r}{n}\right)^{n t} \\ \text { Let } n=1 .\quad & A=P\left(1+\frac{r}{1}\right)^{1 t} \\ \text { Simplify. }\quad & A=P(1+r)^{t} \end{aligned}\)
لنفترض أن\(P\) الدولارات يتم استثمارها في نهاية كل عام. بعد عام واحد، أصبح هذا الإيداع يستحق\(P(1+r)^{1}\) الدولارات، وبعد عام آخر أصبح يستحق\(P(1+r)^{2}\) الدولارات. بعد\(t\) سنوات، سيكون الأمر يستحق\(P(1+r)^{t}\) الدولارات.
| نهاية العام\(1\) | نهاية العام\(2\) | نهاية العام\(3\) | |
|---|---|---|---|
| الإيداع\(P\) الأول في نهاية العام\(1\) | \ (1\) ">\(P\) | \ (2\) ">المبلغ بعد\(1\) عام\(P(1+r)^{1}\) | \ (3\) ">المبلغ بعد\(2\) سنوات\(P(1+r)^{2}\) |
| \(2\)الإيداع\(P\) النهائي في نهاية العام\(2\) | \ (1\) "> | \ (2\) ">\(P\) | \ (3\) ">المبلغ بعد\(1\) عام\(P(1+r)^{1}\) |
| \(3\)الإيداع\(P\) الثالث في نهاية العام\(3\) | \ (1\) "> | \ (2\) "> | \ (3\) ">\(P\) |
بعد ثلاث سنوات، تكون قيمة الأقساط السنوية
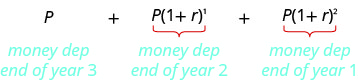
هذا هو مجموع شروط التسلسل الهندسي حيث يكون\(P\) الحد الأول والنسبة المشتركة\(1+r\). نستبدل هذه القيم في صيغة المجموع. كن حذرًا، لدينا استخدامان مختلفان لـ\(r\). الصيغة\(r\) في المجموع هي النسبة الشائعة للتسلسل. في هذه الحالة، هذا\(r\) هو\(1+r\) مكان سعر الفائدة.
\(\begin{aligned} &S_{t} =\frac{a_{1}\left(1-r^{t}\right)}{1-r} \\ \text { Substitute in the values. }\quad & S_{t}=\frac{P\left(1-(1+r)^{t}\right)}{1-(1+r)} \\ \text { Simplify. }\quad & S_{t} =\frac{P\left(1-(1+r)^{t}\right)}{-r} \\ &S_{t} =\frac{P\left((1+r)^{t}-1\right)}{r} \end{aligned}\)
تذكر أن فرضيتنا هي أنه تم إجراء إيداع واحد في نهاية كل عام.
يمكننا تكييف هذه الصيغة\(n\) للودائع التي تتم سنويًا وتضاعف الفائدة\(n\) مرات في السنة.
بالنسبة لرأس المال\(P\)، الذي يتم استثماره في نهاية فترة التجميع، بمعدل فائدة\(r\)، والذي يتم مضاعفته\(n\) مرات في السنة، فإن الرصيد الجديد\(A\)، بعد\(t\) سنوات، هو
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
يقرر الآباء الجدد استثمار $\(100\) شهريًا كمعاش سنوي لابنتهم الرضيعة. سيدفع الحساب\(5\) نسبة فائدة سنوية يتم تجميعها شهريًا. كم سيكون في حساب الطفل في عيد ميلاده الثامن عشر؟
الحل:
للعثور على صيغة المعاش\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)، نحتاج إلى تحديد\(P, r, n\) و\(t\).
حدد\(P\) المبلغ المستثمر كل شهر.
\(P=100\)
حدد\(r\) سعر الفائدة السنوي في شكل عشري.
\(r=0.05\)
حدد\(n\) عدد المرات التي سيتم فيها الإيداع والفائدة المركبة كل عام.
\(n=12\)
حدد\(t\) عدد السنوات.
\(t=18\)
معرفة\(P=100, r=0.05, n=12\)\(t=18\) واستخدام صيغة المجموع.
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
استبدل القيم.
\(A_{t}=\frac{100\left(\left(1+\frac{0.05}{12}\right)^{12.18}-1\right)}{\frac{0.05}{12}}\)
استخدم الآلة الحاسبة للتقييم. تأكد من استخدام الأقواس حسب الحاجة.
\(A_{t}=34.920 .20\)
الإجابة:
سيكون لدى الطفل $\(34,920.20\)
يقرر الأجداد الجدد استثمار $\(200\) شهريًا كمعاش سنوي لحفيدهم. سيدفع الحساب\(5\) نسبة فائدة سنوية يتم تجميعها شهريًا. كم سيكون في حساب الطفل في عيد ميلاده الحادي والعشرين؟
- إجابة
-
$\(88,868.36\)
حصل Arturo للتو على أول وظيفة بدوام كامل بعد تخرجه من الكلية في سنه\(27\). قرر استثمار $\(200\) شهريًا في IRA (سنويًا). الفائدة على الأقساط السنوية هي\(8\)%، والتي يتم تجميعها شهريًا. كم سيكون في حساب Arturo عندما يتقاعد في عيد ميلاده السابع والستين؟
- إجابة
-
$\(698,201.57\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة باستخدام التسلسلات.
المفاهيم الرئيسية
- الحد العام (المصطلح\(n\) العاشر) للتسلسل الهندسي: الحد العام للتسلسل الهندسي مع الحد الأول والنسبة الشائعة\(r\) هو\(a_{1}\)
\(a_{n}=a_{1} r^{n-1}\)
- مجموع الحدود الأولى\(n\) لمتسلسلة هندسية: مجموع\(n\) مصطلحات المتتابعة الهندسية هو\(S_{n}\)
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
أين\(a_{1}\) هو المصطلح الأول\(r\) وهو النسبة المشتركة. المتسلسلة الهندسية اللانهائية: المتسلسلة الهندسية اللانهائية هي\(a_{1}\) مجموع لا نهائي يكون الحد الأول والنسبة الشائعة مكتوبة\(r\)\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
- مجموع المتسلسلة الهندسية اللانهائية: بالنسبة للمتسلسلة الهندسية اللانهائية التي يكون الحد الأول\(a_{1}\) فيها والنسبة الشائعة\(r\)\(|r|<1\)،
إذا كان المجموع هو
\(S=\frac{a_{1}}{1-r}\)
نقول أن السلسلة تتقارب.
إذا كانت\(|r|≥1\) السلسلة الهندسية اللانهائية لا تحتوي على مجموع. نقول أن السلسلة تتباعد.
- قيمة المعاش السنوي مع احتساب الفائدة \(n\)مرات في السنة: بالنسبة لرأس المال\(P\)، الذي يتم استثماره في نهاية الفترة المركبة، بمعدل فائدة\(r\)، والذي يتم مضاعفته\(n\) مرات في السنة، يتم احتساب الرصيد الجديد\(A\)، بعد \(t\)سنوات، هو
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
مسرد المصطلحات
- الأقساط
- الأقساط السنوية هي استثمار عبارة عن سلسلة من الودائع الدورية المتساوية.
- نسبة مشتركة
- النسبة بين الحدود المتتالية في تسلسل هندسي\(\frac{a_{n}}{a_{n-1}}\)، هي النسبة الشائعة\(r\)، حيث تكون\(r\) أكبر من أو تساوي اثنين.
- تسلسل هندسي
- التسلسل الهندسي هو تسلسل تكون فيه النسبة بين المصطلحات المتتالية هي نفسها دائمًا.
- سلسلة هندسية لانهائية
- المتسلسلة الهندسية اللانهائية هي مجموع غير محدود من التسلسل الهندسي اللانهائي.


