12.3: التسلسلات الحسابية
- Page ID
- 201402
في نهاية هذا القسم، ستكون قادرًا على:
- حدد ما إذا كان التسلسل حسابيًا
- ابحث عن الحد العام (\(n\)الحد العاشر) للتسلسل الحسابي
- ابحث عن مجموع الحدود الأولى\(n\) للمتتابعة الحسابية
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بتقييم\(4n−1\) الأعداد الصحيحة\(1, 2, 3\)، و\(4\).
إذا فاتتك هذه المشكلة، راجع المثال 1.6. - حل نظام المعادلات:\(\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.\).
إذا فاتتك هذه المشكلة، راجع المثال 4.9. - إذا\(f(n)=\frac{n}{2}(3 n+5)\)، ابحث\(f(1)+f(20)\).
إذا فاتتك هذه المشكلة، راجع المثال 3.49.
حدد ما إذا كان التسلسل حسابيًا
قدم القسم الأخير التسلسلات والآن سننظر في نوعين محددين من التسلسلات التي لكل منها خصائص خاصة. في هذا القسم سنلقي نظرة على التسلسلات الحسابية وفي القسم التالي، التسلسلات الهندسية.
التسلسل الحسابي هو تسلسل يكون فيه الفرق بين المصطلحات المتتالية ثابتًا. الفرق بين المصطلحات المتتالية في التسلسل الحسابي، a_ {n} -a_ {n-1}\(d\)، هو الفرق المشترك، وهو\(n\) أكبر من أو يساوي اثنين.
التسلسل الحسابي هو تسلسل يكون فيه الفرق بين المصطلحات المتتالية هو نفسه دائمًا.
الفرق بين المصطلحات المتتالية، a_ {n} -a_ {n-1}\(d\)، هو الفرق المشترك، وهو\(n\) أكبر من أو يساوي اثنين.
حدد ما إذا كان كل تسلسل حسابيًا. إذا كان الأمر كذلك، فحدد الفرق المشترك.
- \(5,9,13,17,21,25, \dots\)
- \(4,9,12,17,20,25, \dots\)
- \(10,3,-4,-11,-18,-25, \dots\)
الحل:
لتحديد ما إذا كان التسلسل حسابيًا، نجد فرق الحدود المتتالية الموضحة.
أ.\(\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}\)
التسلسل هو الحساب. الفرق المشترك هو\(d=4\).
ب.\(\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}\)
التسلسل ليس حسابيًا لأن جميع الاختلافات بين الشروط المتتالية ليست هي نفسها. لا يوجد فرق مشترك.
ج.\(\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}\)
الإجابة:
التسلسل هو الحساب. الفرق المشترك هو\(d=-7\).
حدد ما إذا كان كل تسلسل حسابيًا. إذا كان الأمر كذلك، فحدد الفرق المشترك.
- \(9,20,31,42,53,64, \dots\)
- \(12,6,0,-6,-12,-18, \dots\)
- \(7,1,10,4,13,7, \dots\)
- إجابة
-
- التسلسل هو الحساب مع الاختلاف المشترك\(d=11\).
- التسلسل هو الحساب مع الاختلاف المشترك\(d=-6\).
- التسلسل ليس حسابيًا لأن جميع الاختلافات بين الشروط المتتالية ليست هي نفسها.
حدد ما إذا كان كل تسلسل حسابيًا. إذا كان الأمر كذلك، فحدد الفرق المشترك.
- \(-4,4,2,10,8,16, \dots\)
- \(-3,-1,1,3,5,7, \dots\)
- \(7,2,-3,-8,-13,-18, \dots\)
- إجابة
-
- التسلسل ليس حسابيًا لأن جميع الاختلافات بين الشروط المتتالية ليست هي نفسها.
- التسلسل هو الحساب مع الاختلاف المشترك\(d=2\).
- التسلسل هو الحساب مع الاختلاف المشترك\(d=−5\).
إذا عرفنا المصطلح الأول والفرق المشترك\(d\)، فيمكننا سرد عدد محدود من مصطلحات التسلسل.\(a_{1}\)
اكتب الحدود الخمسة الأولى من التسلسل حيث يكون الحد الأول\(5\) والفرق المشترك هو\(d=−6\).
الحل:
نبدأ بالفصل الأول ونضيف الفرق المشترك. ثم نضيف الفرق المشترك لهذه النتيجة للحصول على المصطلح التالي، وهكذا.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}\)
الإجابة:
التسلسل هو\(5,-1,-7,-13,-19, \dots\)
اكتب الحدود الخمسة الأولى من التسلسل حيث يكون الحد الأول\(7\) والفرق المشترك هو\(d=−4\).
- إجابة
-
\(7,3,-1,-5,-9, \dots\)
اكتب الحدود الخمسة الأولى من التسلسل حيث يكون الحد الأول\(11\) والفرق المشترك هو\(d=−8\).
- إجابة
-
\(11,3,-5,-13,-21, \dots\)
أوجد الحد العام (\(n\)الحد العاشر) لمتتابعة حسابية
مثلما وجدنا صيغة للحد العام للتسلسل، يمكننا أيضًا العثور على صيغة للحد العام للتسلسل الحسابي.
دعونا نكتب المصطلحات القليلة الأولى من التسلسل حيث يكون المصطلح الأول\(a_{1}\) والفرق المشترك هو\(d\). سنبحث بعد ذلك عن نمط.
عندما نبحث عن نمط نرى أن كل فصل يبدأ بـ\(a_{1}\).
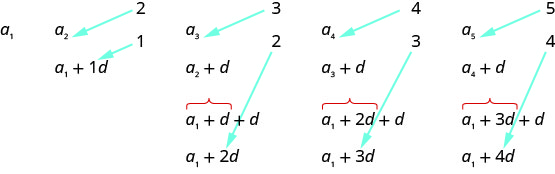
يضيف المصطلح الأول\(0d\) إلى\(a_{1}\)، ويضيف المصطلح الثاني\(1d\)، ويضيف المصطلح الثالث\(2d\)، ويضيف المصطلح الرابع\(3d\)، ويضيف المصطلح الخامس\(4d\). عدد الأشخاص\(ds\) الذين تمت\(a_{1}\) إضافتهم أقل بمقدار واحد من رقم المصطلح. هذا يقودنا إلى ما يلي
\(a_{n}=a_{1}+(n-1) d\)
الحد العام للتسلسل الحسابي مع الحد الأول\(a_{1}\) والفرق المشترك\(d\) هو
\(a_{n}=a_{1}+(n-1) d\)
سنستخدم هذه الصيغة في المثال التالي للعثور على الحد الخامس عشر من التسلسل.
ابحث عن الحد الخامس عشر من التسلسل حيث يكون المصطلح الأول\(3\) والفرق المشترك هو\(6\).
الحل:
\(\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}\)
ابحث عن الحد السابع والعشرين من التسلسل حيث يكون المصطلح الأول\(7\) والفرق المشترك هو\(9\).
- إجابة
-
\(241\)
ابحث عن الحد الثامن عشر من التسلسل حيث يكون الحد الأول\(13\) والفرق المشترك هو\(−7\).
- إجابة
-
\(-106\)
في بعض الأحيان لا نعرف المصطلح الأول ويجب علينا استخدام معلومات أخرى معينة للعثور عليه قبل أن نجد المصطلح المطلوب.
ابحث عن الحد الثاني عشر من التسلسل حيث يكون الحد السابع\(10\) والفرق المشترك هو\(−2\). اكتب صيغة المصطلح العام.
الحل:
للعثور أولاً على المصطلح الأول\(a_{1}\)، استخدم الصيغة مع\(a_{7}=10\)، و\(n=7\)، و\(d=−2\). استبدل القيم. قم بالتبسيط.
\(a_{n}=a_{1}+(n-1) d\)
\(10=a_{1}+(7-1)(-2)\)
\(10=a_{1}+(6)(-2)\)
\(10=a_{1}-12\)
\(a_{1}=22\)
أوجد الحد الثاني عشر\(a_{12}\)، باستخدام الصيغة مع\(a_{1}=22\)، و\(n=12\)، و\(d=-2\). استبدل القيم. قم بالتبسيط.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{12}=22+(12-1)(-2)\)
\(a_{12}=22+(11)(-2)\)
\(a_{12}=0\)
المصطلح الثاني عشر من التسلسل هو\(0, a_{12}=0\)
للعثور على المصطلح العام، استبدل القيم في الصيغة.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{n}=22+(n-1)(-2)\)
\(a_{n}=22-2 n+2\)
الإجابة:
المصطلح العام هو\(a_{n}=-2 n+24\)
ابحث عن الحد الحادي عشر من التسلسل حيث يكون الحد التاسع\(8\) والفرق المشترك هو\(−3\). اكتب صيغة المصطلح العام.
- إجابة
-
\(a_{11}=2 .\)المصطلح العام هو\(a_{n}=-3 n+35\)
ابحث عن الحد التاسع عشر من التسلسل حيث يكون الحد الخامس\(1\) والفرق المشترك هو\(−4\) .أعط صيغة المصطلح العام.
- إجابة
-
\(a_{19}=-55 .\)المصطلح العام هو\(a_{n}=-4 n+21\)
في بعض الأحيان تقودنا المعلومات المقدمة إلى معادلتين في مجهولين. ثم نستخدم طرقنا لحل أنظمة المعادلات للعثور على القيم المطلوبة.
ابحث عن الحد الأول والفرق المشترك للتسلسل حيث يكون الحد الخامس\(19\) والحد الحادي عشر\(37\). اكتب صيغة المصطلح العام.
الحل:
نظرًا لأننا نعرف مصطلحين، يمكننا إنشاء نظام معادلات باستخدام صيغة المصطلح العام.
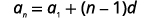 |
|
| نحن نعرف قيمة\(a_{5}\) و\(a_{11}\)، لذلك سوف نستخدم\(n=5\) و\(n=11\). | 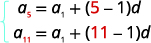 |
استبدل القيم،\(a_{5}=19\) و\(a_{11}=37\). |
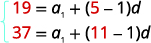 |
| قم بالتبسيط. | 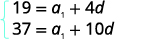 |
| استعد لحذف\(a_{1}\) المصطلح بضرب المعادلة العليا في\(−1\). أضف المعادلات. |
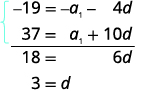 |
| \(d=3\)العودة إلى المعادلة الأولى. | 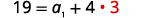 |
| حل لـ\(a_{1}\). |  |
| استخدم الصيغة مع\(a_{1}=7\) و\(d=3\). | 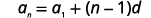 |
| استبدل القيم. | 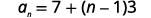 |
| قم بالتبسيط. | 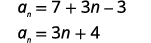 |
| المصطلح الأول هو\(a_{1}=7\). الفرق المشترك هو\(d=3\). |
|
| المصطلح العام للتسلسل هو\(a_{n}=3n+4\). |
الإجابة:
المصطلح العام للتسلسل هو\(a_{n}=3n+4\).
ابحث عن الحد الأول والفرق المشترك للتسلسل حيث يكون المصطلح الرابع هو\(17\) الحد الثالث عشر\(53\). اكتب صيغة المصطلح العام.
- إجابة
-
\(a_{1}=5, d=4 .\)المصطلح العام هو\(a_{n}=4 n+1\).
ابحث عن الحد الأول والفرق المشترك للتسلسل حيث يكون المصطلح الثالث\(2\) والحد الثاني عشر هو\(−25\). اكتب صيغة المصطلح العام.
- إجابة
-
\(a_{1}=8, d=-3 .\)المصطلح العام هو\(a_{n}=-3 n+11\).
أوجد مجموع الحدود الأولى\(n\) للمتتابعة الحسابية
كما هو الحال مع التسلسلات العامة، غالبًا ما يكون من المفيد العثور على مجموع التسلسل الحسابي. يُكتب مجموع\(n\) المصطلحات الأولى لأي تسلسل حسابي كـ\(S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}\).\(S_{n}\) يمكن أن يكون العثور على المبلغ بمجرد إضافة جميع المصطلحات أمرًا شاقًا. لذلك يمكننا أيضًا تطوير صيغة للعثور على مجموع التسلسل باستخدام الحد الأول والأخير من التسلسل.
يمكننا تطوير هذه الصيغة الجديدة من خلال كتابة المجموع أولاً بالبدء بالفصل الأول\(a_{1}\)، والاستمرار في إضافة a\(d\) للحصول على المصطلح التالي على النحو التالي:
\(S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}\).
يمكننا أيضًا عكس ترتيب المصطلحات وكتابة المجموع من خلال البدء بالطرح\(a_{n}\) والاستمرار في الطرح\(d\) للحصول على الحد التالي كـ
\(S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}\).
إذا أضفنا هذين التعبيرين لمجموع الحدود الأولى\(n\) من تسلسل حسابي، يمكننا استخلاص صيغة لمجموع الحدود الأولى\(n\) لأي سلسلة حسابية.
\(\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}\)
نظرًا لوجود\(n\) مجاميع\((a_{1}+a_{n})\) على الجانب الأيمن من المعادلة، نعيد كتابة الجانب الأيمن كـ\(n(a_{1}+a_{n})\).
\(2 S_{n}=n\left(a_{1}+a_{n}\right)\)
نحن نقسم على اثنين لحلها\(S_{n}\).
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
يعطينا هذا صيغة عامة لمجموع الحدود الأولى\(n\) للتسلسل الحسابي.
مجموع\(n\) الشروط الأولى للتسلسل الحسابي هو\(S_{n}\)
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
أين\(a_{1}\) هو المصطلح الأول\(a_{n}\) وهو المصطلح\(n\) العاشر.
نطبق هذه الصيغة في المثال التالي حيث يتم إعطاء المصطلحات القليلة الأولى من التسلسل.
ابحث عن مجموع الحدود الأولى\(30\) للتسلسل الحسابي:\(8, 13, 18, 23, 28, …\)
الحل:
للعثور على المبلغ، سنستخدم الصيغة\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). نحن نعرف\(a_{1}=8, d=5\)\(n=30\)، ولكننا بحاجة إلى البحث من\(a_{n}\) أجل استخدام صيغة المجموع.
ابحث عن\(a_{n}\) المكان\(a_{1}=8, d=5\) و\(n=30\). قم بالتبسيط.
\(\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}\)
معرفة\(a_{1}=8, n=30\) صيغة المجموع واستخدامها.\(a_{30}=153\) استبدل القيم. قم بالتبسيط. قم بالتبسيط.
\(\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}\)
ابحث عن مجموع الحدود الأولى\(30\) للتسلسل الحسابي:\(5, 9, 13, 17, 21, …\)
- إجابة
-
\(1,890\)
ابحث عن مجموع الحدود الأولى\(30\) للتسلسل الحسابي:\(7, 10, 13, 16, 19, …\)
- إجابة
-
\(1,515\)
في المثال التالي، يتم إعطاؤنا المصطلح العام للتسلسل ويطلب منا العثور على مجموع\(50\) المصطلحات الأولى.
أوجد مجموع الحدود الأولى\(50\) للتسلسل الحسابي الذي يكون الحد العام له\(a_{n}=3n−4\).
الحل:
للعثور على المبلغ، سنستخدم الصيغة\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). نحن نعلم\(n=50\)، لكننا بحاجة إلى إيجاد صيغة المجموع\(a_{1}\) ومن\(a_{n}\) أجل استخدامها.
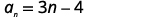 |
|
| ابحث\(a_{1}\) عن طريق الاستبدال\(n=1\). | 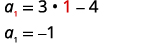 |
| ابحث\(a_{n}\) عن طريق الاستبدال\(n=50\). | 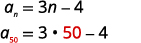 |
| قم بالتبسيط. | 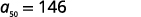 |
| معرفة\(n=50, a_{1}=−1,\)\(a_{50}=146\) واستخدام صيغة المجموع. | 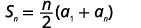 |
| استبدل القيم. | 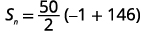 |
| قم بالتبسيط. | 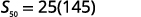 |
| قم بالتبسيط. | 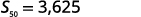 |
أوجد مجموع الحدود الأولى\(50\) للتسلسل الحسابي الذي يكون الحد العام له\(a_{n}=2n−5\).
- إجابة
-
\(2,300\)
أوجد مجموع الحدود الأولى\(50\) للتسلسل الحسابي الذي يكون الحد العام له\(a_{n}=4n+3\).
- إجابة
-
\(5,250\)
في المثال التالي، يتم إعطاؤنا المجموع في تدوين التلخيص. إن إضافة جميع المصطلحات سيكون أمرًا شاقًا، لذلك نقوم باستخراج المعلومات اللازمة لاستخدام الصيغة للعثور على مجموع\(n\) المصطلحات الأولى.
ابحث عن المبلغ:\(\sum_{i=1}^{25}(4 i+7)\).
الحل:
للعثور على المبلغ، سنستخدم الصيغة\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). نحن نعلم\(n=25\)، لكننا بحاجة إلى إيجاد صيغة المجموع\(a_{1}\) ومن\(a_{n}\) أجل استخدامها.
| قم بتوسيع رمز التلخيص. |
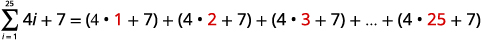
|
| قم بالتبسيط. |
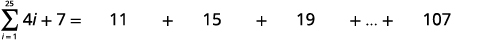
|
| تحديد\(a_{1}\). |  |
| تحديد\(a_{25}\). |

|
| معرفة\(n=25, a_{1}=11\)\(a_{25} = 107\) واستخدام صيغة المجموع. |  |
| استبدل القيم. |  |
| قم بالتبسيط. |  |
| قم بالتبسيط. |  |
ابحث عن المبلغ:\(\sum_{i=1}^{30}(6 i-4)\).
- إجابة
-
\(2,670\)
ابحث عن المبلغ:\(\sum_{i=1}^{35}(5 i-3)\).
- إجابة
-
\(3,045\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام التسلسلات الحسابية
المفاهيم الرئيسية
- الحد العام (المصطلح\(n\) العاشر) للتسلسل
الحسابي المصطلح العام للتسلسل الحسابي مع الحد الأول\(a_{1}\) والفرق المشترك\(d\) هو\(a_{n}=a_{1}+(n-1) d\)
- مجموع الحدود\(n\) الأولى للتسلسل
الحسابي مجموع أول\ حد\(n\) من تسلسل حسابي، أين\(a_{1}\) الحد الأول\(a_{n}\) وهو الحد\(n\) العاشر هو\(S_{n}\)\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
مسرد المصطلحات
- تسلسل حسابي
- التسلسل الحسابي هو تسلسل يكون فيه الفرق بين المصطلحات المتتالية ثابتًا.
- فرق مشترك
- الفرق بين المصطلحات المتتالية في تسلسل حسابي\(a_{n}−a_{n−1}\)\(d\)، هو الفرق المشترك، لأكبر\(n\) من أو يساوي اثنين.


