Skip to main content
Global

12.2E: تمارين

  1. Last updated
  2. Save as PDF
  • Page ID
    201395

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    الممارسة تجعل من الكمال

    التمارين\(\PageIndex{25}\) Write the First Few Terms of a Sequence

    في التمارين التالية، اكتب الحدود الخمسة الأولى من التسلسل الذي يُعطى المصطلح العام.

    1. \(a_{n}=2 n-7\)
    2. \(a_{n}=5 n-1\)
    3. \(a_{n}=3 n+1\)
    4. \(a_{n}=4 n+2\)
    5. \(a_{n}=2^{n}+3\)
    6. \(a_{n}=3^{n}-1\)
    7. \(a_{n}=3^{n}-2 n\)
    8. \(a_{n}=2^{n}-3 n\)
    9. \(a_{n}=\frac{2^{n}}{n^{2}}\)
    10. \(a_{n}=\frac{3^{n}}{n^{3}}\)
    11. \(a_{n}=\frac{4 n-2}{2^{n}}\)
    12. \(a_{n}=\frac{3 n+3}{3^{n}}\)
    13. \(a_{n}=(-1)^{n} \cdot 2 n\)
    14. \(a_{n}=(-1)^{n} \cdot 3 n\)
    15. \(a_{n}=(-1)^{n+1} n^{2}\)
    16. \(a_{n}=(-1)^{n+1} n^{4}\)
    17. \(a_{n}=\frac{(-1)^{n+1}}{n^{2}}\)
    18. \(a_{n}=\frac{(-1)^{n+1}}{2 n}\)
    إجابة

    1. \(-5,-3,-1,1,3\)

    3. \(4,7,10,13,16\)

    5. \(5,7,11,19,35\)

    7. \(1,5,21,73,233\)

    9. \(2,1, \frac{8}{9}, 1, \frac{32}{25}\)

    11. \(1, \frac{3}{2}, \frac{5}{4}, \frac{7}{8}, \frac{9}{16}\)

    13. \(-2,4,-6,8,-10\)

    15. \(1,-4,9,-16,25\)

    17. \(1,-\frac{1}{4}, \frac{1}{9},-\frac{1}{16}, \frac{1}{25}\)

    التمارين\(\PageIndex{26}\) Find a Formula for the General Term (\(n\)th Term) of a Sequence

    في التمارين التالية، ابحث عن حد عام للتسلسل الذي تظهر شروطه الخمسة الأولى.

    1. \(8,16,24,32,40, \dots\)
    2. \(7,14,21,28,35, \ldots\)
    3. \(6,7,8,9,10, \dots\)
    4. \(-3,-2,-1,0,1, \dots\)
    5. \(e^{3}, e^{4}, e^{5}, e^{6}, e^{7}, \ldots\)
    6. \(\frac{1}{e^{2}}, \frac{1}{e}, 1, e, e^{2}, \ldots\)
    7. \(-5,10,-15,20,-25, \dots\)
    8. \(-6,11,-16,21,-26, \dots\)
    9. \(-1,8,-27,64,-125, \dots\)
    10. \(2,-5,10,-17,26, \dots\)
    11. \(-2,4,-6,8,-10, \dots\)
    12. \(1,-3,5,-7,9, \dots\)
    13. \(\frac{1}{4}, \frac{1}{16}, \frac{1}{64}, \frac{1}{256}, \frac{1}{1,024}, \dots\)
    14. \(\frac{1}{1}, \frac{1}{8}, \frac{1}{27}, \frac{1}{64}, \frac{1}{125}, \dots\)
    15. \(-\frac{1}{2},-\frac{2}{3},-\frac{3}{4},-\frac{4}{5},-\frac{5}{6}, \dots\)
    16. \(-2,-\frac{3}{2},-\frac{4}{3},-\frac{5}{4},-\frac{6}{5}, \dots\)
    17. \(-\frac{5}{2},-\frac{5}{4},-\frac{5}{8},-\frac{5}{16},-\frac{5}{32}, \dots\)
    18. \(4, \frac{1}{2}, \frac{4}{27}, \frac{4}{64}, \frac{4}{125}, \dots\)
    إجابة

    1. \(a_{n}=8 n\)

    3. \(a_{n}=n+5\)

    5. \(a_{n}=e^{n+2}\)

    7. \(a_{n}=(-1)^{n} 5 n\)

    9. \(a_{n}=(-1)^{n} n^{3}\)

    11. \(a_{n}=(-1)^{n} 2 n\)

    13. \(a_{n}=\frac{1}{4^{n}}\)

    15. \(a_{n}=-\frac{n}{n+1}\)

    17. \(-\frac{5}{2^{n}}\)

    التمارين\(\PageIndex{27}\) Use Factorial Notation

    في التمارين التالية، باستخدام الترميز العاملي، اكتب المصطلحات الخمسة الأولى من التسلسل الذي يُعطى المصطلح العام.

    1. \(a_{n}=\frac{4}{n !}\)
    2. \(a_{n}=\frac{5}{n !}\)
    3. \(a_{n}=3 n !\)
    4. \(a_{n}=2 n !\)
    5. \(a_{n}=(2 n) !\)
    6. \(a_{n}=(3 n) !\)
    7. \(a_{n}=\frac{(n-1) !}{(n) !}\)
    8. \(a_{n}=\frac{n !}{(n+1) !}\)
    9. \(a_{n}=\frac{n !}{n^{2}}\)
    10. \(a_{n}=\frac{n^{2}}{n !}\)
    11. \(a_{n}=\frac{(n+1) !}{n^{2}}\)
    12. \(a_{n}=\frac{(n+1) !}{2 n}\)
    إجابة

    1. \(4,2, \frac{2}{3}, \frac{1}{6}, \frac{1}{30}\)

    3. \(3,6,18,72,360\)

    5. \(2,24,720,40320,3628800\)

    7. \(1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}\)

    9. \(1, \frac{1}{2}, \frac{2}{3}, \frac{3}{2}, \frac{24}{5}\)

    11. \(2, \frac{3}{2}, \frac{8}{3}, \frac{15}{2}, \frac{144}{5}\)

    التمارين\(\PageIndex{28}\) Find the Partial Sum

    في التمارين التالية، قم بتوسيع المبلغ الجزئي والعثور على قيمته.

    1. \(\sum_{i=1}^{5} i^{2}\)
    2. \(\sum_{i=1}^{5} i^{3}\)
    3. \(\sum_{i=1}^{6}(2 i+3)\)
    4. \(\sum_{i=1}^{6}(3 i-2)\)
    5. \(\sum_{i=1}^{4} 2^{i}\)
    6. \(\sum_{i=1}^{4} 3^{i}\)
    7. \(\sum_{k=0}^{3} \frac{4}{k !}\)
    8. \(\sum_{k=0}^{4}-\frac{1}{k !}\)
    9. \(\sum_{k=1}^{5} k(k+1)\)
    10. \(\sum_{k=1}^{5} k(2 k-3)\)
    11. \(\sum_{n=1}^{5} \frac{n}{n+1}\)
    12. \(\sum_{n=1}^{4} \frac{n}{n+2}\)
    إجابة

    1. \(1+4+9+16+25=55\)

    3. \(5+7+9+11+13+15=60\)

    5. \(2+4+8+16=30\)

    7. \(\frac{4}{1}+\frac{4}{1}+\frac{4}{2}+\frac{4}{6}+\frac{32}{3}=10 \frac{2}{3}\)

    9. \(2+6+12+20+30=70\)

    11. \(\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\frac{4}{5}+\frac{5}{6}=\frac{71}{20}\)

    التمارين\(\PageIndex{29}\) Use Summation Notation to Write a Sum

    في التمارين التالية، اكتب كل مجموع باستخدام رمز الجمع.

    1. \(\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}\)
    2. \(\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\frac{1}{256}\)
    3. \(1+\frac{1}{8}+\frac{1}{27}+\frac{1}{64}+\frac{1}{125}\)
    4. \(\frac{1}{5}+\frac{1}{25}+\frac{1}{125}+\frac{1}{625}\)
    5. \(2+1+\frac{2}{3}+\frac{1}{2}+\frac{2}{5}\)
    6. \(3+\frac{3}{2}+1+\frac{3}{4}+\frac{3}{5}+\frac{1}{2}\)
    7. \(3-6+9-12+15\)
    8. \(-5+10-15+20-25\)
    9. \(-2+4-6+8-10+\ldots+20\)
    10. \(1-3+5-7+9+\ldots+21\)
    11. \(14+16+18+20+22+24+26\)
    12. \(9+11+13+15+17+19+21\)
    إجابة

    1. \(\sum_{n=1}^{5} \frac{1}{3^{n}}\)

    3. \(\sum_{n=1}^{5} \frac{1}{n^{3}}\)

    5. \(\sum_{n=1}^{5} \frac{2}{n}\)

    7. \(\sum_{n=1}^{5}(-1)^{n+1} 3 n\)

    9. \(\sum_{n=1}^{10}(-1)^{n} 2 n\)

    11. \(\sum_{n=1}^{7}(2 n+12)\)

    التمارين\(\PageIndex{30}\) Writing Exercises
    1. بكلماتك الخاصة، اشرح كيفية كتابة شروط التسلسل عندما تعرف الصيغة. اعرض مثالاً لتوضيح شرحك.
    2. ما حدود التسلسل التي تكون سالبة عندما يكون حد التسلسل\(a_{n}=(-1)^{n}(n+2)\)؟\(n^{th}\)
    3. بكلماتك الخاصة، اشرح المقصود\(n!\) بعرض بعض الأمثلة لتوضيح تفسيرك.
    4. اشرح\(\sum_{k=1}^{12} 2 k\) معنى كل جزء من الترميز.
    إجابة

    1. سوف تتنوع الإجابات.

    3. سوف تتنوع الإجابات.

    فحص ذاتي

    أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

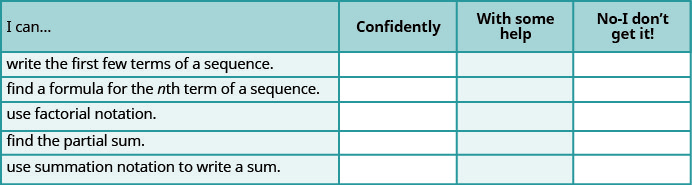
    يوضِّح هذا الشكل جدولًا يحتوي على أربعة أعمدة وستة صفوف. الصف الأول هو صف العنوان وتسميات كل عمود، «أستطيع»، «بثقة»، «مع بعض المساعدة»، و «لا أفهم ذلك!». يقرأ الصف الأول في العمود الثاني «اكتب المصطلحات القليلة الأولى من التسلسل»، بينما يقرأ الصف الثالث، العمود الأول، «ابحث عن صيغة للحد التاسع من التسلسل»، يقرأ الصف الرابع العمود الأول «استخدم الترميز العاملي، الصف الخامس، يقرأ العمود الأول، ابحث عن المجموع الجزئي»، والصف الأخير، الأول يقرأ العمود «استخدم رمز التلخيص لكتابة المجموع». الأعمدة والصفوف الثلاثة المتبقية فارغة.
    الشكل 12.1.24

    ب- إذا كانت معظم الشيكات الخاصة بك هي:

    ... بثقة. تهانينا! لقد حققت الأهداف في هذا القسم. فكر في مهارات الدراسة التي استخدمتها حتى تتمكن من الاستمرار في استخدامها. ماذا فعلت لتصبح واثقًا من قدرتك على القيام بهذه الأشياء؟ كن محددًا.

    ... مع بعض المساعدة. يجب معالجة هذا بسرعة لأن الموضوعات التي لا تتقنها تصبح ثقوبًا في طريقك إلى النجاح. في الرياضيات، يعتمد كل موضوع على العمل السابق. من المهم التأكد من أن لديك أساسًا قويًا قبل المضي قدمًا. من الذي يمكنك طلب المساعدة؟ يعتبر زملائك في الفصل والمدرب موارد جيدة. هل يوجد مكان في الحرم الجامعي حيث يتوفر مدرسو الرياضيات؟ هل يمكن تحسين مهاراتك الدراسية؟

    ... لا - أنا لا أفهم ذلك! هذه علامة تحذير ويجب ألا تتجاهلها. يجب أن تحصل على المساعدة على الفور وإلا ستصاب بالارتباك بسرعة. راجع مدرسك في أقرب وقت ممكن لمناقشة وضعك. معًا يمكنك وضع خطة للحصول على المساعدة التي تحتاجها.