12.2: التسلسلات
- Page ID
- 201385
في نهاية هذا القسم، ستكون قادرًا على:
- اكتب المصطلحات القليلة الأولى من التسلسل
- ابحث عن صيغة للمصطلح العام (الحد النوني) للتسلسل
- استخدم الترميز العاملي
- ابحث عن المبلغ الجزئي
- استخدم رمز التلخيص لكتابة المجموع
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بتقييم\(2n+3\) الأعداد الصحيحة\(1, 2, 3\)، و\(4\).
إذا فاتتك هذه المشكلة، راجع المثال 1.6. - قم بتقييم\((−1)^{n}\) الأعداد الصحيحة\(1, 2, 3\)، و\(4\).
إذا فاتتك هذه المشكلة، راجع المثال 1.19. - إذا\(f(n)=n^{2}+2\)، ابحث\(f(1)+f(2)+f(3)\).
إذا فاتتك هذه المشكلة، راجع المثال 3.49.
اكتب الشروط القليلة الأولى من التسلسل
دعونا ننظر إلى الدالة\(f(x)=2x\) ونقيمها لأرقام العد فقط.
| \(f(x)=2x\) | |
| \(x\) | \(2x\) |
| \(1\) | \(2\) |
| \(2\) | \(4\) |
| \(3\) | \(6\) |
| \(4\) | \(8\) |
| \(5\) | \(10\) |
| \(...\) | \(...\) |
إذا قمنا بإدراج قيم الدالة بالترتيب كـ\(2, 4, 6, 8\)، و\(10\)،... فلدينا تسلسل. التسلسل هو دالة يكون مجالها هو أرقام العد.
التسلسل هو دالة يكون مجالها هو أرقام العد.
يمكن أيضًا رؤية التسلسل كقائمة مرتبة من الأرقام وكل رقم في القائمة هو مصطلح. قد يحتوي التسلسل على عدد لا نهائي من المصطلحات أو عدد محدود من المصطلحات. يحتوي التسلسل الخاص بنا على ثلاث نقاط (علامة الحذف) في النهاية مما يشير إلى أن القائمة لا تنتهي أبدًا. إذا كان المجال هو مجموعة جميع أرقام العد، فإن التسلسل هو تسلسل لا نهائي. مجاله هو جميع أرقام العد وهناك عدد لا حصر له من أرقام العد.
\(2,4,6,8,10, \dots\)
إذا قصرنا المجال على عدد محدود من أرقام العد، فإن التسلسل هو تسلسل محدود. إذا استخدمنا أرقام العد الأربعة الأولى فقط، فسيكون التسلسل\(1, 2, 3, 4\) الخاص بنا هو التسلسل المحدود،
\(2,4,6,8\)
في كثير من الأحيان عند العمل مع التسلسلات، لا نريد كتابة جميع المصطلحات. نريد طريقة أكثر إحكاما لإظهار كيفية تعريف كل مصطلح. عندما عملنا مع الوظائف، كتبنا\(f(x)=2x\) وقلنا أن التعبير\(2x\) هو القاعدة التي تحدد القيم في النطاق. في حين أن التسلسل عبارة عن دالة، فإننا لا نستخدم رمز الدالة المعتاد. بدلاً من كتابة الدالة كـ\(f(x)=2x\)، سنكتبها كـ\(a_{n}=2n\). \(a_{n}\)هذا هو\(n\) الحد العاشر من التسلسل، وهو المصطلح الموجود\(n\) في الموضع حيث\(n\) توجد قيمة في المجال. تُسمى صيغة كتابة الحد\(n\) العاشر من التسلسل بالمصطلح العام أو صيغة التسلسل.
تم العثور على المصطلح العام للتسلسل من صيغة كتابة المصطلح\(n\) العاشر من التسلسل. الحد\(n\) العاشر من التسلسل\(a_{n}\)، هو المصطلح الموجود\(n\) في الموضع الذي\(n\) توجد فيه قيمة في المجال.
عندما نحصل على الحد العام للتسلسل، يمكننا إيجاد المصطلحات عن طريق استبدالها\(n\) بأرقام العد بالترتيب. من أجل\(a_{n}=2 n\)،
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(a_{n}\) | 2\(\cdot 1\) | 2\(\cdot 2\) | 2\(\cdot 3\) | 2\(\cdot 4\) | 2\(\cdot 5\) | 2\(\cdot 6\) |
| \(2\) | \(4\) | \(6\) | \(8\) | \(10\) |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)
\(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)
للعثور على قيم التسلسل، نستبدل أرقام العد بالترتيب في الحد العام للتسلسل.
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=4 n-3\).
الحل:
نستبدل القيم\(1, 2, 3, 4\)\(5\)، وفي الصيغة\(a_{n}=4n−3\)، بالترتيب.
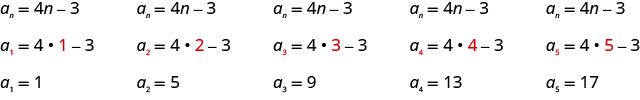
الإجابة:
المصطلحات الخمسة الأولى من التسلسل هي\(1, 5, 9, 13\)، و\(17\).
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=3n-4\).
- إجابة
-
\(-1,2,5,8,11\)
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=2n-5\).
- إجابة
-
\(-3,-1,1,3,5\)
بالنسبة لبعض التسلسلات، يكون المتغير هو الأس.
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=2^{n}+1\).
الحل:
نستبدل القيم\(1, 2, 3, 4\)\(5\)، وفي الصيغة\(a_{n}=2^{n}+1\)، بالترتيب.
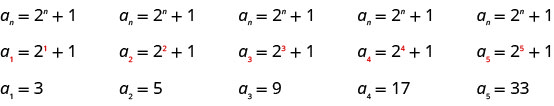
الإجابة:
المصطلحات الخمسة الأولى من التسلسل هي\(3, 5, 9, 17\)، و\(33\).
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=3^{n}+4\).
- إجابة
-
\(7,13,31,85,247\)
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=2^{n}-5\).
- إجابة
-
\(-3,-1,3,11,27\)
ليس من غير المألوف رؤية التعبيرات\((−1)^{n}\) أو\((−1)^{n+1}\) المصطلح العام للتسلسل. إذا قمنا بتقييم كل من هذه التعبيرات لبعض القيم، فإننا نرى أن هذا التعبير يبدل علامة المصطلحات.
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \ (n\) ">\((-1)^{n}\) | \ (1\) ">\((-1)^{1}\) \(-1\) |
\ (2\) ">\((-1)^{2}\) 1 |
\ (3\) ">\((-1)^{3}\) \(-1\) |
\ (4\) ">\((-1)^{4}\) \(1\) |
\ (5\) ">\((-1)^{5}\) \(-1\) |
| \ (n\) ">\((-1)^{n+1}\) | \ (1\) ">\((-1)^{1+1}\) 1 |
\ (2\) ">\((-1)^{2+1}\) \(-1\) |
\ (3\) ">\((-1)^{3+1}\) 1 |
\ (4\) ">\((-1)^{4+1}\) \(-1\) |
\ (5\) ">\((-1)^{5+1}\) 1 |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)
\(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=(-1)^{n} n^{3}\).
الحل:
نستبدل القيم\(1, 2, 3, 4\)\(5\)، وفي الصيغة\(a_{n}=(-1)^{n} n^{3}\)، بالترتيب.
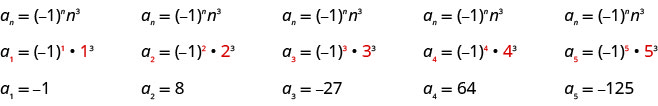
الإجابة:
المصطلحات الخمسة الأولى من التسلسل هي\(−1, 8, −27, 64, −1, 8, −27, 64\)، و\(−125\).
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=(-1)^{n} n^{2}\).
- إجابة
-
\(-1,4,-9,16,-25\)
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=(-1)^{n+1} n^{3}\).
- إجابة
-
\(1,-8,27,-64,125\)
ابحث عن صيغة للمصطلح العام (\(n\)الحد العاشر) من التسلسل
في بعض الأحيان يكون لدينا بعض المصطلحات للتسلسل وسيكون من المفيد معرفة المصطلح العام\(n\) أو المصطلح. للعثور على المصطلح العام، نبحث عن الأنماط في المصطلحات. غالبًا ما تتضمن الأنماط مضاعفات أو قوى. نحن نبحث أيضًا عن نمط في علامات المصطلحات.
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى. \(4,8,12,16,20, \dots\)
الحل:
-


نحن نبحث عن نمط في المصطلحات. 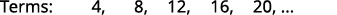
الأرقام كلها مضاعفات لـ\(4\). 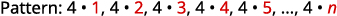
المصطلح العام للتسلسل هو\(a_{n}=4n\). الجدول 12-1-4 الإجابة:
المصطلح العام للتسلسل هو\(a_{n}=4n\).
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى.
\(3,6,9,12,15, \dots\)
- إجابة
-
\(a_{n}=3 n\)
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى.
\(5,10,15,20,25, \dots\)
- إجابة
-
\(a_{n}=5 n\)
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى. \(2,-4,8,-16,32, \dots\)
الحل:
-
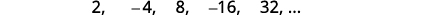
الشكل 12.1.8 
الشكل 12.1.9 نحن نبحث عن نمط في المصطلحات. 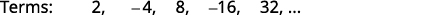
الشكل 12.1.10 الأرقام هي قوى لـ\(2\). العلامات متناوبة، حتى وإن كانت\(n\) سلبية. 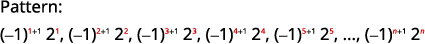
الشكل 12.1.11 المصطلح العام للتسلسل هو\(a_{n}=(-1)^{n+1} 2^{n}\) الجدول 12-1-5 الإجابة:
المصطلح العام للتسلسل هو\(a_{n}=(-1)^{n+1}2^{n}\).
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى.
\(-3,9,-27,81,-243, \dots\)
- إجابة
-
\(a_{n}=(-1)^{n} 3^{n}\)
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى
\(1,-4,9,-16,25, \dots\)
- إجابة
-
\(a_{n}=(-1)^{n+1} n^{2}\)
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)
الحل:
-
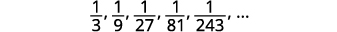
الشكل 12.1.12 
الشكل 12.1.13 نحن نبحث عن نمط في المصطلحات. 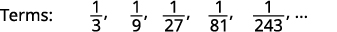
الشكل 12.1.14 البسط كلها\(1\). 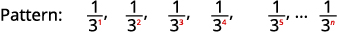
الشكل 12.1.15 القواسم هي قوى\(3\). المصطلح العام للتسلسل هو\(a_{n}=\frac{1}{3^{n}}\). الجدول 12-1-6 الإجابة:
المصطلح العام للتسلسل هو\(a_{n}=\frac{1}{3^{n}}\).
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى.
\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)
- إجابة
-
\(a_{n}=\frac{1}{2^{n}}\)
ابحث عن مصطلح عام للتسلسل الذي تظهر شروطه الخمسة الأولى.
\(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)
- إجابة
-
\(a_{n}=\frac{1}{n^{2}}\)
استخدم الترميز العاملي
غالبًا ما تحتوي التسلسلات على مصطلحات هي منتجات الأعداد الصحيحة المتتالية. نشير إلى هذه المنتجات برمز خاص يسمى الترميز العاملي. على سبيل المثال\(5!\)،\(5\) اقرأ العامل، يعني\(5⋅4⋅3⋅2⋅1\). علامة التعجب ليست علامات ترقيم هنا؛ إنها تشير إلى الترميز العاملي.
إذا كان\(n\) عددًا صحيحًا موجبًا،\(n!\) فسيكون
\(n !=n(n-1)(n-2) \dots\)
نحن\(0!\) نعرّف على أنه\(1\)، لذلك\(0!=1\).
يتم عرض\(n!\) قيم الأعداد الصحيحة\(5\) الموجبة الأولى.
\(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=\frac{1}{n !}\).
الحل:
نستبدل القيم\(1, 2, 3, 4, 5\) في الصيغة\(a_{n}=\frac{1}{n !}\)، بالترتيب.
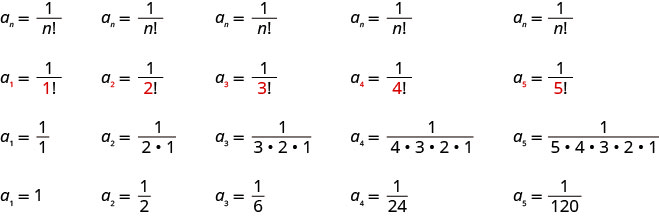
الإجابة:
المصطلحات الخمسة الأولى من التسلسل هي\(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\).
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=\frac{2}{n !}\).
- إجابة
-
\(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=\frac{3}{n !}\).
- إجابة
-
\(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)
عندما يكون هناك كسر يحتوي على عوامل في البسط والمقام، فإننا نصطف العوامل رأسيًا لتسهيل العمليات الحسابية.
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=\frac{(n+1) !}{(n-1) !}\).
الحل:
نستبدل القيم\(1, 2, 3, 4, 5\) في الصيغة\(a_{n}=\frac{(n+1) !}{(n-1) !}\)، بالترتيب.
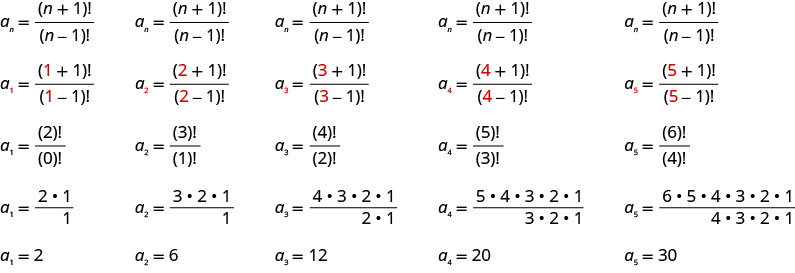
الإجابة:
المصطلحات الخمسة الأولى من التسلسل هي\(2, 6, 12, 20\)، و\(30\).
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=\frac{(n-1) !}{(n+1) !}\)
- إجابة
-
\(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)
اكتب الحدود الخمسة الأولى من التسلسل الذي يكون الحد العام له\(a_{n}=\frac{n !}{(n+1) !}\).
- إجابة
-
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)
ابحث عن المجموع الجزئي
في بعض الأحيان في التطبيقات، بدلاً من مجرد سرد المصطلحات، من المهم بالنسبة لنا إضافة شروط التسلسل. بدلاً من مجرد ربط المصطلحات بعلامات الجمع، يمكننا استخدام رمز التلخيص.
على سبيل المثال،\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\) يمكن كتابتها كـ\(\sum_{i=1}^{5} a_{i}\). نقرأ هذا على أنه «مجموع\(a\) الفرعي\(i\) من\(i\) يساوي واحدًا إلى خمسة». الرمز\(∑\) يعني الإضافة\(i\) وهو فهرس التلخيص. \(1\)يخبرنا من أين نبدأ (القيمة الأولية)\(5\) ويخبرنا أين ننتهي (القيمة النهائية).
مجموع\(n\) المصطلحات الأولى من التسلسل الذي تمت كتابة المصطلح\(n\) الثالث\(a_{n}\) به في تدوين التلخيص على النحو التالي:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
\(i\)هذا هو فهرس التلخيص\(1\) ويخبرنا من أين نبدأ\(n\) ويخبرنا من أين ننتهي.
عندما نضيف عددًا محدودًا من المصطلحات، فإننا نسمي المجموع بمبلغ جزئي.
قم بتوسيع المبلغ الجزئي وابحث عن قيمته:\(\sum_{i=1}^{5} 2 i\).
الحل:
-
\(\sum_{i=1}^{5} 2 i\) نحن نستبدل القيم\(1, 2, 3, 4, 5\) بالترتيب. \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\) قم بالتبسيط. \(2+4+6+8+10\) أضف. \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\) الجدول 12-1.7 الإجابة:
\(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
قم بتوسيع المبلغ الجزئي وابحث عن قيمته:\(\sum_{i=1}^{5} 3 i\).
- إجابة
-
\(45\)
قم بتوسيع المبلغ الجزئي وابحث عن قيمته:\(\sum_{i=1}^{5} 4 i\).
- إجابة
-
\(60\)
لا يجب أن يكون الفهرس دائمًا هو\(i\) أننا نستطيع استخدام أي حرف، ولكن\(i\)\(k\) يتم استخدامه بشكل شائع. لا يجب أن يبدأ الفهرس بأي\(1\) منهما - يمكن أن يبدأ وينتهي بأي عدد صحيح موجب.
قم بتوسيع المبلغ الجزئي وابحث عن قيمته:\(\sum_{k=0}^{3} \frac{1}{k !}\).
الحل:
\(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)
قم بتوسيع المبلغ الجزئي وابحث عن قيمته:\(\sum_{k=0}^{3} \frac{2}{k !}\).
- إجابة
-
\(\frac{16}{3}\)
قم بتوسيع المبلغ الجزئي وابحث عن قيمته:\(\sum_{k=0}^{3} \frac{3}{k !}\).
- إجابة
-
\(8\)
استخدم رمز التلخيص لكتابة مجموع
في المثالين الأخيرين، انتقلنا من تدوين التلخيص إلى كتابة المجموع. الآن سنبدأ بمجموع ونغيره إلى تدوين التلخيص. هذا مشابه جدًا لإيجاد المصطلح العام للتسلسل. سنحتاج إلى إلقاء نظرة على المصطلحات والعثور على نمط. غالبًا ما تتضمن الأنماط مضاعفات أو قوى.
اكتب المجموع باستخدام رمز التلخيص:\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\).
الحل:
\(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)
اكتب المجموع باستخدام رمز التلخيص:\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\).
- إجابة
-
\(\sum_{n=1}^{5} \frac{1}{2^{n}}\)
اكتب المجموع باستخدام رمز التلخيص:\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)
- إجابة
-
\(\sum_{n=1}^{5} \frac{1}{n^{2}}\)
عندما تحتوي شروط المبلغ على معاملات سالبة، يجب علينا تحليل نمط العلامات بعناية.
اكتب المجموع باستخدام رمز التلخيص:\(-1+8-27+64-125\).
الحل:
-
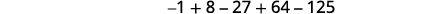
الشكل 12.1.18 
الشكل 12.1.19 نحن نبحث عن نمط في المصطلحات. 
الشكل 12.1.20 تتناوب علامات المصطلحات،
وتكون المصطلحات الفردية سلبية.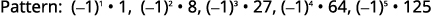
الشكل 12.1.21 الأرقام هي مكعبات أرقام
العد من واحد إلى خمسة.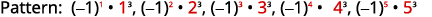
الشكل 12.1.22 
الشكل 12.1.23 المجموع المكتوب في تدوين التلخيص هو \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\) الجدول 12-1-8
اكتب كل مجموع باستخدام رمز الجمع:\(1-4+9-16+25\).
- إجابة
-
\(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)
اكتب كل مجموع باستخدام رمز الجمع:\(-2+4-6+8-10\).
- إجابة
-
\(\sum_{n=1}^{5}(-1)^{n} 2 n\)
قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة باستخدام التسلسلات.
المفاهيم الرئيسية
- الترميز العاملي
إذا كان\(n\) عددًا صحيحًا موجبًا،\(n!\) فسيكون
\(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)
نحن نعرّف\(0!\) على النحو\(1\) التالي:\(0!=1\)
- تدوين التلخيص
مجموع\(n\) المصطلحات الأولى من التسلسل الذي تمت كتابة المصطلح\(n\) الثالث\(a_{n}\) به في تدوين التلخيص على النحو التالي:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
\(i\)هذا هو فهرس التلخيص\(1\) ويخبرنا من أين نبدأ\(n\) ويخبرنا من أين ننتهي.
مسرد المصطلحات
- تسلسل محدود
- تسلسل ذو مجال يقتصر على عدد محدود من أرقام العد.
- مصطلح عام للتسلسل
- المصطلح العام للتسلسل هو صيغة كتابة الحد\(n\) العاشر من التسلسل. الحد\(n\) العاشر من التسلسل\(a_{n}\)، هو المصطلح الموجود\(n\) في الموضع الذي\(n\) توجد فيه قيمة في المجال.
- تسلسل لانهائي
- تسلسل يشمل نطاقه جميع الأرقام ويوجد عدد لا نهائي من أرقام العد.
- مبلغ جزئي
- عندما نضيف عددًا محدودًا من مصطلحات التسلسل، فإننا نسمي المجموع المجموع الجزئي.
- تسلسل
- التسلسل هو دالة يكون مجالها هو أرقام العد.


