الفصل 11 تمارين المراجعة

تمارين مراجعة الفصل

معادلات المسافة ونقطة المنتصف؛ الدوائر

التمارين\(\PageIndex{1}\) Use the Distance Formula

في التمارين التالية، ابحث عن المسافة بين النقاط. قرِّب إلى أقرب جزء من عشرة إذا لزم الأمر.

1. \((-5,1)\)و\((-1,4)\)
2. \((-2,5)\)و\((1,5)\)
3. \((8,2)\)و\((-7,-3)\)
4. \((1,-4)\)و\((5,-5)\)

إجابة

2. \(d=3\)

4. \(d=\sqrt{17}, d \approx 4.1\)

التمارين\(\PageIndex{2}\) Use the Midpoint Formula

في التمارين التالية، ابحث عن نقطة منتصف المقاطع المستقيمة التي تُعطى نقاط نهايتها.

1. \((-2,-6)\)و\((-4,-2)\)
2. \((3,7)\)و\((5,1)\)
3. \((-8,-10)\)و\((9,5)\)
4. \((-3,2)\)و\((6,-9)\)

إجابة

2. \((4,4)\)

4. \(\left(\frac{3}{2},-\frac{7}{2}\right)\)

التمارين\(\PageIndex{3}\) Write the Equation of a Circle in Standard Form

في التمارين التالية، اكتب الشكل القياسي لمعادلة الدائرة بالمعلومات المعطاة.

1. نصف القطر هو\(15\) والمركز هو\((0,0)\)
2. نصف القطر هو\(\sqrt{7}\) والمركز هو\((0,0)\)
3. نصف القطر هو\(9\) والمركز هو\((-3,5)\)
4. نصف القطر هو\(7\) والمركز هو\((-2,-5)\)
5. المركز هو\((3,6)\) والنقطة على الدائرة هي\((3,-2)\)
6. المركز هو\((2,2)\) والنقطة على الدائرة هي\((4,4)\)

إجابة

2. \(x^{2}+y^{2}=7\)

4. \((x+2)^{2}+(y+5)^{2}=49\)

6. \((x-2)^{2}+(y-2)^{2}=8\)

التمارين\(\PageIndex{4}\) Graph a Circle

في التمارين التالية،

1. ابحث عن المركز ونصف القطر، ثم
2. رسم بياني لكل دائرة.

1. \(2 x^{2}+2 y^{2}=450\)
2. \(3 x^{2}+3 y^{2}=432\)
3. \((x+3)^{2}+(y-5)^{2}=81\)
4. \((x+2)^{2}+(y+5)^{2}=49\)
5. \(x^{2}+y^{2}-6 x-12 y-19=0\)
6. \(x^{2}+y^{2}-4 y-60=0\)

إجابة

2.

1. نصف القطر:\(12,\) المركز:\((0,0)\)

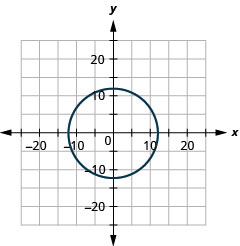
الشكل 11-هاء-1

4.

1. نصف القطر:\(7,\) المركز:\((-2,-5)\)

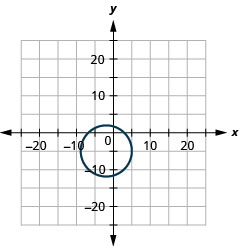
الشكل 11-هاء-2

6.

1. نصف القطر:\(8,\) المركز:\((0,2)\)

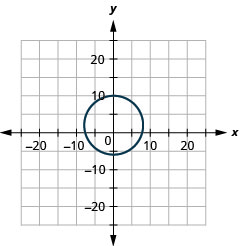
الشكل 11-هاء-3

بارابولاس

التمارين\(\PageIndex{5}\) Graph Vertical Parabolas

في التمارين التالية، قم برسم بياني لكل معادلة باستخدام خصائصها.

1. \(y=x^{2}+4 x-3\)
2. \(y=2 x^{2}+10 x+7\)
3. \(y=-6 x^{2}+12 x-1\)
4. \(y=-x^{2}+10 x\)

إجابة

2.

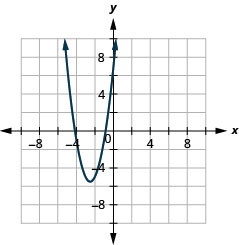
الشكل 11-هاء-4

4.

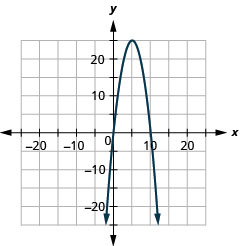
الشكل 11-هاء-5

التمارين\(\PageIndex{6}\) Graph Vertical Parabolas

في التمارين التالية،

1. اكتب المعادلة في الصورة القياسية، ثم
2. استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.

1. \(y=x^{2}+4 x+7\)
2. \(y=2 x^{2}-4 x-2\)
3. \(y=-3 x^{2}-18 x-29\)
4. \(y=-x^{2}+12 x-35\)

إجابة

2.

1. \(y=2(x-1)^{2}-4\)

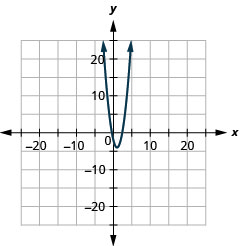
الشكل 11 هاء -6

4.

1. \(y=-(x-6)^{2}+1\)

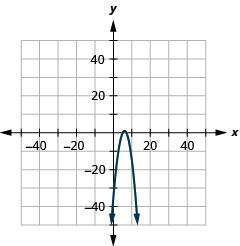
الشكل 11 هاء - 7

التمارين\(\PageIndex{7}\) Graph Horizontal Parabolas

في التمارين التالية، قم برسم بياني لكل معادلة باستخدام خصائصها.

1. \(x=2 y^{2}\)
2. \(x=2 y^{2}+4 y+6\)
3. \(x=-y^{2}+2 y-4\)
4. \(x=-3 y^{2}\)

إجابة

2.

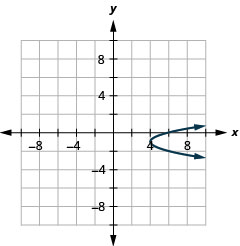
الشكل 11 هاء -8

4.

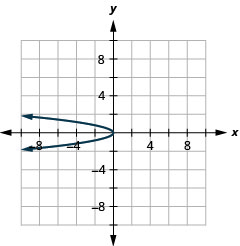
الشكل 11 هاء - 9

التمارين\(\PageIndex{8}\) Graph Horizontal Parabolas

في التمارين التالية،

1. اكتب المعادلة في الصورة القياسية، ثم
2. استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.

1. \(x=4 y^{2}+8 y\)
2. \(x=y^{2}+4 y+5\)
3. \(x=-y^{2}-6 y-7\)
4. \(x=-2 y^{2}+4 y\)

إجابة

2.

1. \(x=(y+2)^{2}+1\)

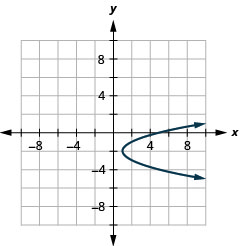
الشكل 11 هاء -10

4.

1. \(x=-2(y-1)^{2}+2\)

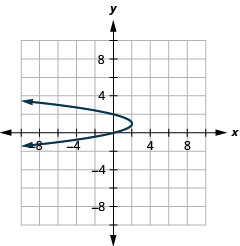
الشكل 11 هاء -11

التمارين\(\PageIndex{9}\) Solve Applications with Parabolas

في التمارين التالية، قم بإنشاء معادلة القوس المكافئ المتشكل في أساس الجسر الموضح. أعط الإجابة في النموذج القياسي.

1.

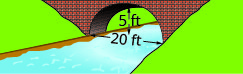
الشكل 11 هاء - 12

2.

الشكل 11 هاء - 13

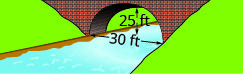
إجابة

2. \(y=-\frac{1}{9} x^{2}+\frac{10}{3} x\)

الأشكال البيضاوية

التمارين\(\PageIndex{10}\) Graph an Ellipse with Center at the Origin

في التمارين التالية، قم برسم بياني لكل شكل بيضاوي.

1. \(\frac{x^{2}}{36}+\frac{y^{2}}{25}=1\)
2. \(\frac{x^{2}}{4}+\frac{y^{2}}{81}=1\)
3. \(49 x^{2}+64 y^{2}=3136\)
4. \(9 x^{2}+y^{2}=9\)

إجابة

2.

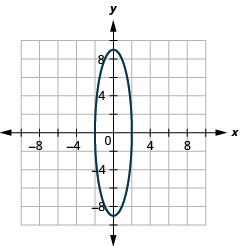
الشكل 11 هاء - 14

4.

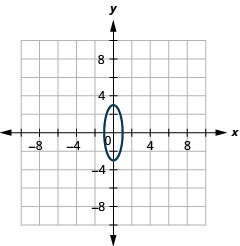
الشكل 11 هاء - 15

التمارين\(\PageIndex{11}\) Find the Equation of an Ellipse with Center at the Origin

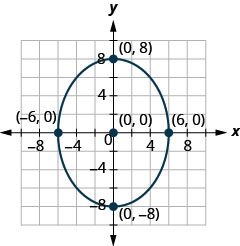
في التمارين التالية، أوجد معادلة الشكل البيضاوي الموضَّح في الرسم البياني.

1.

الشكل 11 هاء - 16

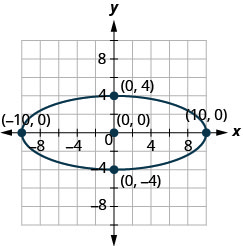
2.

الشكل 11 هاء - 17

إجابة

2. \(\frac{x^{2}}{36}+\frac{y^{2}}{64}=1\)

التمارين\(\PageIndex{12}\) Graph an Ellipse with Center Not at the Origin

في التمارين التالية، قم برسم بياني لكل شكل بيضاوي.

1. \(\frac{(x-1)^{2}}{25}+\frac{(y-6)^{2}}{4}=1\)
2. \(\frac{(x+4)^{2}}{16}+\frac{(y+1)^{2}}{9}=1\)
3. \(\frac{(x-5)^{2}}{16}+\frac{(y+3)^{2}}{36}=1\)
4. \(\frac{(x+3)^{2}}{9}+\frac{(y-2)^{2}}{25}=1\)

إجابة

2.

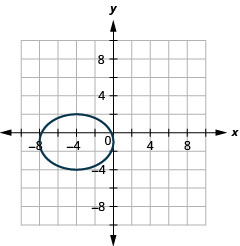
الشكل 11 هاء - 18

4.

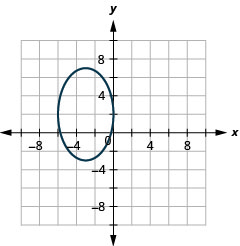
الشكل 11 هاء -19

التمارين\(\PageIndex{13}\) Graph an Ellipse with Center Not at the Origin

في التمارين التالية،

1. اكتب المعادلة في الصورة القياسية و
2. رسم بياني.

1. \(x^{2}+y^{2}+12 x+40 y+120=0\)
2. \(25 x^{2}+4 y^{2}-150 x-56 y+321=0\)
3. \(25 x^{2}+4 y^{2}+150 x+125=0\)
4. \(4 x^{2}+9 y^{2}-126 x+405=0\)

إجابة

2.

1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)

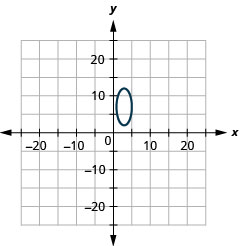
الشكل 11 هاء -20

4.

1. \(\frac{x^{2}}{9}+\frac{(y-7)^{2}}{4}=1\)

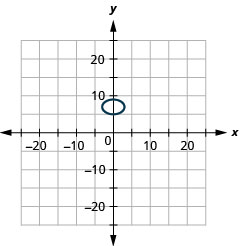
الشكل 11 هاء - 21

التمارين\(\PageIndex{14}\) Solve Applications with Ellipses

في التمارين التالية، اكتب معادلة الشكل البيضاوي الموصوف.

1. يتحرك المذنب في مدار بيضاوي حول الشمس. أقرب ما يصل إليه المذنب إلى الشمس هو\(10\) AU تقريبًا والأبعد هو\(90\) AU تقريبًا. الشمس هي واحدة من بؤر المدار البيضاوي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار الإهليلجي للمذنب.

الشكل 11 هاء - 22

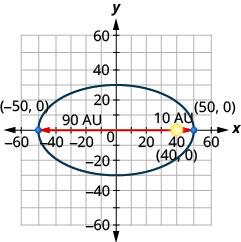
إجابة

1. حل

الغلو

التمارين\(\PageIndex{15}\) Graph a Hyperbola with Center at \((0,0)\)

في التمارين التالية، رسم بياني.

1. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
2. \(\frac{y^{2}}{49}-\frac{x^{2}}{16}=1\)
3. \(9 y^{2}-16 x^{2}=144\)
4. \(16 x^{2}-4 y^{2}=64\)

إجابة

1.

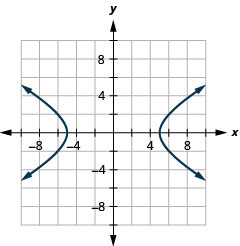
الشكل 11 هاء - 23

3.

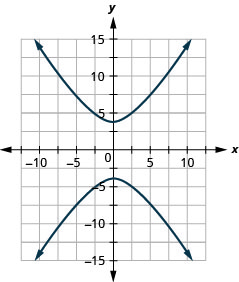
الشكل 11 هاء - 24

التمارين\(\PageIndex{16}\) Graph a Hyperbola with Center at \((h,k)\)

في التمارين التالية، رسم بياني.

1. \(\frac{(x+1)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
3. \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{9}=1\)
4. \(\frac{(y-1)^{2}}{25}-\frac{(x-2)^{2}}{9}=1\)

إجابة

1.

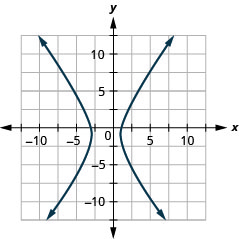
الشكل 11 هاء - 25

3.

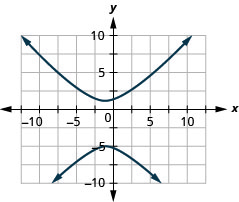
الشكل 11 هاء - 26

التمارين\(\PageIndex{17}\) Graph a Hyperbola with Center at \((h,k)\)

في التمارين التالية،

1. اكتب المعادلة في الصورة القياسية و
2. رسم بياني.

1. \(4 x^{2}-16 y^{2}+8 x+96 y-204=0\)
2. \(16 x^{2}-4 y^{2}-64 x-24 y-36=0\)
3. \(4 y^{2}-16 x^{2}+32 x-8 y-76=0\)
4. \(36 y^{2}-16 x^{2}-96 x+216 y-396=0\)

إجابة

1.

1. \(\frac{(x+1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)

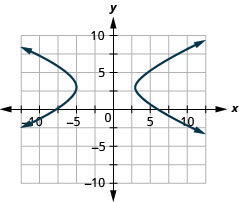
الشكل 11 هاء - 27

3.

1. \(\frac{(y-1)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)

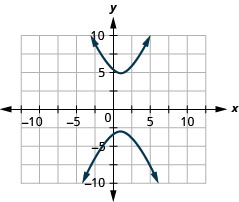
الشكل 11 هاء - 28

التمارين\(\PageIndex{18}\) Identify the Graph of Each Equation as a Circle, Parabola, Ellipse, or Hyperbola

في التمارين التالية، حدد نوع الرسم البياني.

1. 1. \(16 y^{2}-9 x^{2}-36 x-96 y-36=0\)
   2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
   3. \(y=x^{2}-2 x+3\)
   4. \(25 x^{2}+9 y^{2}=225\)
2. 1. \(x^{2}+y^{2}+4 x-10 y+25=0\)
   2. \(y^{2}-x^{2}-4 y+2 x-6=0\)
   3. \(x=-y^{2}-2 y+3\)
   4. \(16 x^{2}+9 y^{2}=144\)

إجابة

1.

1. هايبربولا
2. دائرة
3. بارابولا
4. الشكل البيضاوي

حل أنظمة المعادلات غير الخطية

التمارين\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Graphing

في التمارين التالية، قم بحل نظام المعادلات باستخدام الرسوم البيانية.

1. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y=-5}\end{array}\right.\)

إجابة

1.

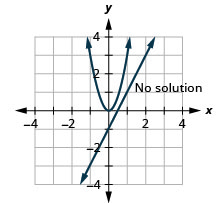
الشكل 11 هاء - 29

3.

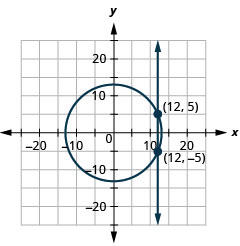
الشكل 11 هاء -30

التمارين\(\PageIndex{20}\) Solve a System of Nonlinear Equations Using Substitution

في التمارين التالية، قم بحل نظام المعادلات باستخدام الاستبدال.

1. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=-2 x+2}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x-y=4}\end{array}\right.\)
3. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {y-x=5}\end{array}\right.\)
4. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)

إجابة

1. \((-1,4)\)

3. لا يوجد حل

التمارين\(\PageIndex{21}\) Solve a System of Nonlinear Equations Using Elimination

في التمارين التالية، قم بحل نظام المعادلات باستخدام الحذف.

1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y-1=0}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{x^{2}-y^{2}=5} \\ {-2 x^{2}-3 y^{2}=-30}\end{array}\right.\)
3. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {3 y^{2}-4 x=12}\end{array}\right.\)
4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=14} \\ {x^{2}-y^{2}=16}\end{array}\right.\)

إجابة

1. \((-\sqrt{7}, 3),(\sqrt{7}, 3)\)

3. \((-3,0),(0,-2),(0,2)\)

التمارين\(\PageIndex{22}\) Use a System of Nonlinear Equations to Solve Applications

في التمارين التالية، قم بحل المشكلة باستخدام نظام المعادلات.

1. مجموع مربعات الرقمين هو\(25\). الفرق بين الأرقام هو\(1\). ابحث عن الأرقام.
2. الفرق بين مربعي الرقمين هو\(45\). الفرق بين مربع الرقم الأول وضعف مربع الرقم الثاني هو\(9\). ابحث عن الأرقام.
3. محيط المستطيل يساوي\(58\) الأمتار ومساحته بالمتر\(210\) المربع. أوجد طول المستطيل وعرضه.
4. اشترى كولتون ميكرويف أكبر لمطبخه. يبلغ قطر الجزء الأمامي من الميكروويف\(34\) بوصات. تحتوي الواجهة أيضًا على مساحة بوصة\(480\) مربعة. ما طول وعرض الميكروويف؟

إجابة

1. \(-3\)و\(-4\) أو\(4\) و\(3\)

3. إذا كان الطول\(14\) بالبوصة، يكون العرض\(15\) بوصات. إذا كان الطول\(15\) بالبوصة، يكون العرض\(14\) بوصات.

اختبار الممارسة

التمارين\(\PageIndex{23}\)

في التمارين التالية، أوجد المسافة بين النقاط ونقطة منتصف المقطع المستقيم بنقاط النهاية المُعطاة. قم بتقريبه لأقرب جزء من عشرة حسب الحاجة.

1. \((-4,-3)\)و\((-10,-11)\)
2. \((6,8)\)و\((-5,-3)\)

إجابة

1. المسافة:\(10,\) نقطة الوسط:\((-7,-7)\)

التمارين\(\PageIndex{24}\)

في التمارين التالية، اكتب الشكل القياسي لمعادلة الدائرة بالمعلومات المعطاة.

1. نصف القطر هو\(11\) والمركز هو\((0,0)\)
2. نصف القطر هو\(12\) والمركز هو\((10,-2)\)
3. المركز هو\((-2,3)\) والنقطة على الدائرة هي\((2,-3)\)
4. أوجد معادلة الشكل البيضاوي الموضَّح في الرسم البياني.

الشكل 11 هاء - 31

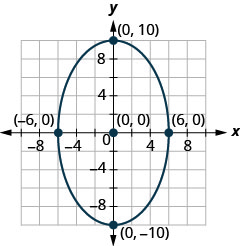
إجابة

1. \(x^{2}+y^{2}=121\)

3. \((x+2)^{2}+(y-3)^{2}=52\)

التمارين\(\PageIndex{25}\)

في التمارين التالية،

1. حدد نوع الرسم البياني لكل معادلة في صورة دائرة أو مكافئ أو شكل بيضاوي أو هايبربولا، و
2. رسم المعادلة بيانيًا.

1. \(4 x^{2}+49 y^{2}=196\)
2. \(y=3(x-2)^{2}-2\)
3. \(3 x^{2}+3 y^{2}=27\)
4. \(\frac{y^{2}}{100}-\frac{x^{2}}{36}=1\)
5. \(\frac{x^{2}}{16}+\frac{y^{2}}{81}=1\)
6. \(x=2 y^{2}+10 y+7\)
7. \(64 x^{2}-9 y^{2}=576\)

إجابة

1.

1. الشكل البيضاوي

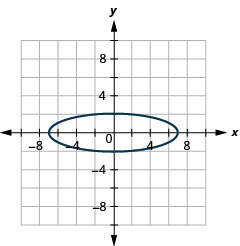
الشكل 11 هاء - 32

3.

1. دائرة

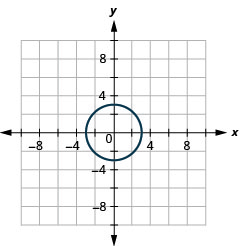
الشكل 11 هاء - 33

5.

1. الشكل البيضاوي

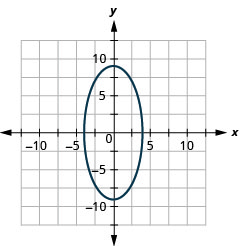
الشكل 11 هاء - 34

7.

1. هايبربولا

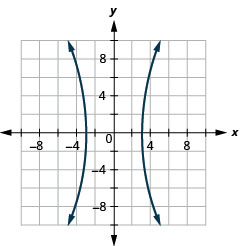
الشكل 11 هاء - 35

التمارين\(\PageIndex{26}\)

في التمارين التالية،

1. حدد نوع الرسم البياني لكل معادلة في صورة دائرة أو مكافئ أو بيضاوي أو هيبربولا،
2. اكتب المعادلة في الصورة القياسية، و
3. رسم المعادلة بيانيًا.

1. \(25 x^{2}+64 y^{2}+200 x-256 y-944=0\)
2. \(x^{2}+y^{2}+10 x+6 y+30=0\)
3. \(x=-y^{2}+2 y-4\)
4. \(9 x^{2}-25 y^{2}-36 x-50 y-214=0\)
5. \(y=x^{2}+6 x+8\)
6. حل نظام المعادلات غير الخطية بالرسم البياني:\(\left\{\begin{array}{l}{3 y^{2}-x=0} \\ {y=-2 x-1}\end{array}\right.\).
7. حل نظام المعادلات غير الخطية باستخدام الاستبدال:\(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {y=-x-4}\end{array}\right.\).
8. حل نظام المعادلات غير الخطية باستخدام الحذف:\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
9. أوجد معادلة القوس المكافئ المتكوَّن في أساس الجسر الموضَّح. أعط الإجابة في\(y=a x^{2}+b x+c\) النموذج.

الشكل 11 هاء - 36

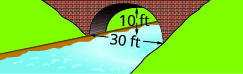
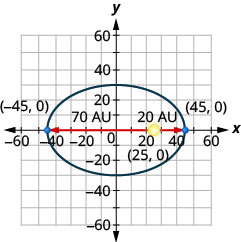
10. يتحرك مذنب في مدار بيضاوي حول الشمس. أقرب ما يصل إليه المذنب إلى الشمس هو\(20\) AU تقريبًا والأبعد هو\(70\) AU تقريبًا. الشمس هي واحدة من بؤر المدار البيضاوي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار الإهليلجي للمذنب.

الشكل 11 هاء - 37

11. مجموع الرقمين هو\(22\) والمنتج هو\(−240\). ابحث عن الأرقام.

12. في عيد ميلادها، اشترى أجداد أوليف لها جهاز تلفزيون بشاشة عريضة جديدة. قبل فتحه، تريد التأكد من أنه يناسب مركز الترفيه الخاص بها. التلفزيون هو\(55\)». يتم قياس حجم التلفزيون على قطر الشاشة ويبلغ طول الشاشة العريضة أكبر من العرض. تحتوي الشاشة أيضًا على مساحة بوصة\(1452\) مربعة. يحتوي مركز الترفيه الخاص بها على ملحق للتلفزيون بطول\(50\) بوصة وعرض\(40\) بوصة. ما هو طول وعرض شاشة التلفزيون وهل ستناسب مركز أوليف الترفيهي؟

إجابة

2.

1. دائرة
2. \((x+5)^{2}+(y+3)^{2}=4\)

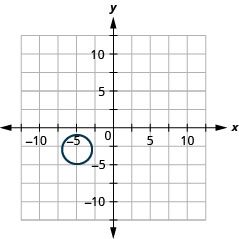
الشكل 11 هاء - 38

4.

1. هايبربولا
2. \(\frac{(x-2)^{2}}{25}-\frac{(y+1)^{2}}{9}=1\)

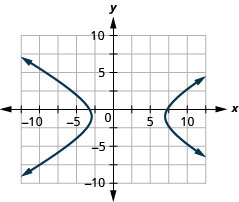
الشكل 11 هاء - 39

6. لا يوجد حل

8. \((0,-3),(0,3)\)

10. \(\frac{x^{2}}{2025}+\frac{y^{2}}{1400}=1\)

12. الطول هو\(44\) بوصة والعرض هو\(33\) بوصة. سوف يتناسب التلفزيون مع مركز Olive الترفيهي.

مسرد المصطلحات

نظام المعادلات غير الخطية

نظام المعادلات غير الخطية هو نظام لا تكون فيه واحدة على الأقل من المعادلات خطية.