10.5: استخدم خصائص اللوغاريتمات
- Page ID
- 201616
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم خصائص اللوغاريتمات
- استخدم تغيير الصيغة الأساسية
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- تقييم: أ.\(a^{0}\) ب\(a^{1}\).
إذا فاتتك هذه المشكلة، راجع المثال 5.14. - اكتب باستخدام الأس العقلاني:\(\sqrt[3]{x^{2} y}\).
إذا فاتتك هذه المشكلة، راجع المثال 8.27. - تقريبًا إلى ثلاث منازل عشرية:\(2.5646415\).
إذا فاتتك هذه المشكلة، راجع المثال 1.34.
استخدم خصائص اللوغاريتمات
الآن بعد أن تعلمنا عن الدوال الأسية واللوغاريتمية، يمكننا تقديم بعض خصائص اللوغاريتمات. ستكون هذه مفيدة جدًا بينما نواصل حل المعادلات الأسية واللوغاريتمية.
تُستمد الخاصيتان الأوليان من تعريف اللوغاريتمات. نظرًا لأنه\(a^{0}=1\) يمكننا تحويل هذا إلى شكل لوغاريتمي والحصول عليه\(\log _{a} 1=0\). أيضًا، منذ\(a^{1}=a\) ذلك الحين نحصل على\(\log _{a} a=1\).
خصائص اللوغاريتمات
\(\log _{a} 1=0 \quad \log _{a} a=1\)
في المثال التالي يمكننا تقييم اللوغاريتم عن طريق التحويل إلى الصورة الأسية، كما فعلنا سابقًا، ولكن التعرف على الخصائص ثم تطبيقها يوفر الوقت.
قم بالتقييم باستخدام خصائص اللوغاريتمات:
- \(\log _{8} 1\)
- \(\log _{6} 6\)
الحل:
أ.
\(\log _{8} 1\)
استخدم الخاصية،\(\log _{a} 1=0\).
\(0 \quad \log _{8} 1=0\)
ب.
\(\log _{6} 6\)
استخدم الخاصية،\(\log _{a} a=1\).
\(1 \quad \log _{6} 6=1\)
قم بالتقييم باستخدام خصائص اللوغاريتمات:
- \(\log _{13} 1\)
- \(\log _{9} 9\)
- إجابة
-
- \(0\)
- \(1\)
قم بالتقييم باستخدام خصائص اللوغاريتمات:
- \(\log _{5} 1\)
- \(\log _{7} 7\)
- إجابة
-
- \(0\)
- \(1\)
يمكن أيضًا التحقق من الخاصيتين التاليتين بتحويلهما من الصورة الأسية إلى الصورة اللوغاريتمية، أو العكس.
\(a^{\log _{a} x}=x\)تتحول المعادلة الأسية إلى المعادلة اللوغاريتمية\(\log _{a} x=\log _{a} x\)، وهي عبارة حقيقية للقيم الموجبة\(x\) فقط.
\(\log _{a} a^{x}=x\)تتحول المعادلة اللوغاريتمية إلى المعادلة الأسية\(a^{x}=a^{x}\)، وهي أيضًا عبارة حقيقية.
تسمى هاتان الخاصيتان بالخصائص العكسية لأنه عندما تكون لدينا نفس القاعدة، فإن رفع السجل إلى قوة «يلغي» السجل ويجعل السجل «يتراجع» عن الارتفاع إلى قوة. توضح هاتان الخاصيتان تكوين الوظائف. انتهى كلاهما بدالة الهوية التي توضح مرة أخرى أن الدوال الأسية واللوغاريتمية هي دوال عكسية.
الخصائص العكسية للوغاريتمات
من أجل\(a>0, x>0\)\(a \neq 1\) و
\(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)
في المثال التالي، قم بتطبيق الخصائص العكسية للوغاريتمات.
قم بالتقييم باستخدام خصائص اللوغاريتمات:
- \(4^{\log _{4} 9}\)
- \(\log _{3} 3^{5}\)
الحل:
أ.
\(4^{\log _{4} 9}\)
استخدم الخاصية،\(a^{\log _{a} x}=x\).
\(9 \quad 4^{\log _{4} 9}=9\)
ب.
\(\log _{3} 3^{5}\)
استخدم الخاصية،\(a^{\log _{a} x}=x\).
\(5 \quad \log _{3} 3^{5}=5\)
قم بالتقييم باستخدام خصائص اللوغاريتمات:
- \(5^{\log _{5} 15}\)
- \(\log _{7} 7^{4}\)
- إجابة
-
- \(15\)
- \(4\)
قم بالتقييم باستخدام خصائص اللوغاريتمات:
- \(2^{\log _{2} 8}\)
- \(\log _{2} 2^{15}\)
- إجابة
-
- \(8\)
- \(15\)
هناك ثلاث خصائص أخرى للوغاريتمات التي ستكون مفيدة في عملنا. نحن نعلم أن الدوال الأسية والدالة اللوغاريتمية مترابطتان جدًا. يوضح تعريفنا للوغاريتم أن اللوغاريتم هو أس المكافئ الأسي. تحتوي خصائص الأسس على خصائص ذات صلة بالأسس.
في خاصية المنتج الخاصة بالأسس\(a^{m} \cdot a^{n}=a^{m+n}\)، نرى أنه لضرب نفس القاعدة، نضيف الأسس. \(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)تخبرنا خاصية المنتج الخاصة باللوغاريتمات بأخذ سجل المنتج، ونضيف سجل العوامل.
خاصية المنتج للوغاريتمات
إذا\(M>0, N>0, \mathrm{a}>0\)\(\mathrm{a} \neq 1,\) ثم
\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\)
لوغاريتم المنتج هو مجموع اللوغاريتمات.
نحن نستخدم هذه الخاصية لكتابة سجل المنتج كمجموع سجلات كل عامل.
استخدم خاصية المنتج للوغاريتمات لكتابة كل لوغاريتم كمجموع اللوغاريتمات. قم بالتبسيط، إن أمكن:
- \(\log _{3} 7 x\)
- \(\log _{4} 64 x y\)
الحل:
أ.
\(\log _{3} 7 x\)
استخدم خاصية المنتج،\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\).
\(\log _{3} 7+\log _{3} x\)
\(\log _{3} 7 x=\log _{3} 7+\log _{3} x\)
ب.
\(\log _{4} 64 x y\)
استخدم خاصية المنتج،\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\).
\(\log _{4} 64+\log _{4} x+\log _{4} y\)
قم بتبسيط التقييم,\(\log _{4} 64\).
\(3+\log _{4} x+\log _{4} y\)
\(\log _{4} 64 x y=3+\log _{4} x+\log _{4} y\)
استخدم خاصية المنتج للوغاريتمات لكتابة كل لوغاريتم كمجموع اللوغاريتمات. قم بالتبسيط، إن أمكن:
- \(\log _{3} 3 x\)
- \(\log _{2} 8 x y\)
- إجابة
-
- \(1+\log _{3} x\)
- \(3+\log _{2} x+\log _{2} y\)
استخدم خاصية المنتج للوغاريتمات لكتابة كل لوغاريتم كمجموع اللوغاريتمات. قم بالتبسيط، إن أمكن:
- \(\log _{9} 9 x\)
- \(\log _{3} 27 x y\)
- إجابة
-
- \(1+\log _{9} x\)
- \(3+\log _{3} x+\log _{3} y\)
وبالمثل، في خاصية حاصل القسمة للأسس\(\frac{a^{m}}{a^{n}}=a^{m-n}\)، نرى أنه لتقسيم نفس القاعدة، نطرح الأسس. \(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)تخبرنا خاصية حاصل القسمة للوغاريتمات بأخذ لوغاريتمات، ونطرح لوغاريتمات البسط والمقام.
خاصية حاصل القسمة للوغاريتمات
إذا\(M>0, N>0, \mathrm{a}>0\)\(\mathrm{a} \neq 1,\) ثم
\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)
لوغاريتم القسمة هو الفرق بين اللوغاريتمات.
لاحظ ذلك\(\log _{a} M=\log _{a} N \not=\log _{a}(M-N)\).
نحن نستخدم هذه الخاصية لكتابة سجل حاصل القسمة كفرق في سجلات كل عامل.
استخدم خاصية خارج القسمة للوغاريتمات لكتابة كل لوغاريتم كفرق في اللوغاريتمات. قم بالتبسيط، إن أمكن.
- \(\log _{5} \frac{5}{7}\)
- \(\log \frac{x}{100}\)
الحل:
أ.
\(\log _{5} \frac{5}{7}\)
استخدم خاصية حاصل القسمة،\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\).
\(\log _{5} 5-\log _{5} 7\)
قم بالتبسيط.
\(1-\log _{5} 7\)
\(\log _{5} \frac{5}{7}=1-\log _{5} 7\)
ب.
\(\log \frac{x}{100}\)
استخدم خاصية حاصل القسمة،\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\).
\(\log x-\log 100\)
قم بالتبسيط.
\(\log x-2\)
\(\log \frac{x}{100}=\log x-2\)
استخدم خاصية خارج القسمة للوغاريتمات لكتابة كل لوغاريتم كفرق في اللوغاريتمات. قم بالتبسيط، إن أمكن.
- \(\log _{4} \frac{3}{4}\)
- \(\log \frac{x}{1000}\)
- إجابة
-
- \(\log _{4} 3-1\)
- \(\log x-3\)
استخدم خاصية خارج القسمة للوغاريتمات لكتابة كل لوغاريتم كفرق في اللوغاريتمات. قم بالتبسيط، إن أمكن.
- \(\log _{2} \frac{5}{4}\)
- \(\log \frac{10}{y}\)
- إجابة
-
- \(\log _{2} 5-2\)
- \(1-\log y\)
ترتبط الخاصية الثالثة للوغاريتمات بخاصية قوة الأسس\(\left(a^{m}\right)^{n}=a^{m \cdot n}\)، ونرى أنه لرفع القوة إلى قوة، نضرب الأسس. \(\log _{a} M^{p}=p \log _{a} M\)تخبرنا خاصية القوة في اللوغاريتمات بأخذ سجل الرقم المرفوع إلى قوة، ونضرب القوة في سجل الرقم.
خاصية قوة اللوغاريتمات
إذا كان\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\)\(p\) هناك أي رقم حقيقي إذن،
\(\log _{a} M^{p}=p \log _{a} M\)
سجل الرقم الذي تم رفعه إلى طاقة كمنتج الطاقة مضروبًا في سجل الرقم.
نحن نستخدم هذه الخاصية لكتابة سجل الرقم الذي تم رفعه إلى قوة كناتج الطاقة مضروبًا في سجل الرقم. نأخذ الأس بشكل أساسي ونرميه أمام اللوغاريتم.
استخدم خاصية قوة اللوغاريتمات لكتابة كل لوغاريتم كمنتج للوغاريتمات. قم بالتبسيط، إن أمكن.
- \(\log _{5} 4^{3}\)
- \(\log x^{10}\)
الحل:
أ.
\(\log _{5} 4^{3}\)
استخدم خاصية الطاقة،\(\log _{a} M^{p}=p \log _{a} M\).
3\(\log _{5} 4\)
\(\log _{5} 4^{3}=3 \log _{5} 4\)
ب.
\(\log x^{10}\)
استخدم خاصية الطاقة،\(\log _{a} M^{p}=p \log _{a} M\).
\(10\log x\)
\(\log x^{10}=10 \log x\)
استخدم خاصية قوة اللوغاريتمات لكتابة كل لوغاريتم كمنتج للوغاريتمات. قم بالتبسيط، إن أمكن.
- \(\log _{7} 5^{4}\)
- \(\log x^{100}\)
- إجابة
-
- \(4\log _{7} 5\)
- 100\(\cdot \log x\)
استخدم خاصية قوة اللوغاريتمات لكتابة كل لوغاريتم كمنتج للوغاريتمات. قم بالتبسيط، إن أمكن.
- \(\log _{2} 3^{7}\)
- \(\log x^{20}\)
- إجابة
-
- \(7\log _{2} 3\)
- \(20\cdot \log x\)
نلخص خصائص اللوغاريتمات هنا لسهولة الرجوع إليها. في حين أن اللوغاريتمات الطبيعية هي حالة خاصة لهذه الخصائص، إلا أنه غالبًا ما يكون من المفيد أيضًا عرض نسخة اللوغاريتم الطبيعية لكل خاصية.
خصائص اللوغاريتمات
إذا كان\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\)\(p\) هناك أي رقم حقيقي إذن،
| الملكية | قاعدة\(a\) | قاعدة\(e\) |
|---|---|---|
| \ (a\) ">\(\log _{a} 1=0\) | \ (e\) ">\(\ln 1=0\) | |
| \ (a\) ">\(\log _{a} a=1\) | \ (e\) ">\(\ln e=1\) | |
| الخصائص العكسية | \ (a\) ">\(a^{\log _{a} x}=x\) \(\log _{a} a^{x}=x\) |
\ (e\) ">\(e^{\ln x}=x\) \(\ln e^{x}=x\) |
| خاصية المنتج للوغاريتمات | \ (a\) ">\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) | \ (e\) ">\(\ln (M \cdot N)=\ln M+\ln N\) |
| خاصية حاصل القسمة للوغاريتمات | \ (a\) ">\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) | \ (e\) ">\(\ln \frac{M}{N}=\ln M-\ln N\) |
| خاصية قوة اللوغاريتمات | \ (a\) ">\(\log _{a} M^{p}=p \log _{a} M\) | \ (e\) ">\(\ln M^{p}=p \ln M\) |
الآن لدينا الخصائص، يمكننا استخدامها «لتوسيع» التعبير اللوغاريتمي. هذا يعني كتابة اللوغاريتم كمجموع أو فرق وبدون أي صلاحيات.
نطبق بشكل عام خصائص المنتج والقسمة قبل تطبيق خاصية الطاقة.
استخدم خصائص اللوغاريتمات لتوسيع اللوغاريتم\(\log _{4}\left(2 x^{3} y^{2}\right)\). قم بالتبسيط، إن أمكن.
الحل:
استخدم خاصية المنتج،\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\).
استخدم خاصية الطاقة،\(\log _{a} M^{p}=p \log _{a} M\)، في المصطلحين الأخيرين. قم بالتبسيط.
استخدم خصائص اللوغاريتمات لتوسيع اللوغاريتم\(\log _{2}\left(5 x^{4} y^{2}\right)\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\log _{2} 5+4 \log _{2} x+2 \log _{2} y\)
استخدم خصائص اللوغاريتمات لتوسيع اللوغاريتم\(\log _{3}\left(7 x^{5} y^{3}\right)\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\log _{3} 7+5 \log _{3} x+3 \log _{3} y\)
عندما يكون لدينا جذر في التعبير اللوغاريتمي، فمن المفيد أولاً كتابة راديباند كأس عقلاني.
استخدم خصائص اللوغاريتمات لتوسيع اللوغاريتم\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\). قم بالتبسيط، إن أمكن.
الحل
\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\)
أعد كتابة الجذر باستخدام الأس العقلاني.
\(\log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)^{\frac{1}{4}}\)
استخدم خاصية الطاقة،\(\log _{a} M^{p}=p \log _{a} M\).
\(\frac{1}{4} \log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)\)
استخدم خاصية حاصل القسمة،\(\log _{a} M \cdot N=\log _{a} M-\log _{a} N\).
\(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\log _{2}\left(3 y^{2} z\right)\right)\)
استخدم خاصية المنتج،\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)، في الفصل الثاني.
\(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\left(\log _{2} 3+\log _{2} y^{2}+\log _{2} z\right)\right)\)
استخدم خاصية الطاقة\(\log _{a} M^{p}=p \log _{a} M\)، داخل الأقواس.
\(\frac{1}{4}\left(3 \log _{2} x-\left(\log _{2} 3+2 \log _{2} y+\log _{2} z\right)\right)\)
قم بالتبسيط من خلال التوزيع
\(\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)
\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}=\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)
استخدم خصائص اللوغاريتمات لتوسيع اللوغاريتم\(\log _{4} \sqrt[5]{\frac{x^{4}}{2 y^{3} z^{2}}}\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\frac{1}{5}\left(4 \log _{4} x-\frac{1}{2}-3 \log _{4} y-2 \log _{4} z\right)\)
استخدم خصائص اللوغاريتمات لتوسيع اللوغاريتم\(\log _{3} \sqrt[3]{\frac{x^{2}}{5 y z}}\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\frac{1}{3}\left(2 \log _{3} x-\log _{3} 5-\log _{3} y-\log _{3} z\right)\)
عكس توسيع اللوغاريتم هو تكثيف مجموع أو اختلاف اللوغاريتمات التي لها نفس القاعدة في لوغاريتم واحد. نستخدم مرة أخرى خصائص اللوغاريتمات لمساعدتنا، ولكن في الاتجاه المعاكس.
لتكثيف التعبيرات اللوغاريتمية ذات القاعدة نفسها في لوغاريتم واحد، نبدأ باستخدام خاصية الطاقة للحصول على معاملات مصطلحات السجل لتكون واحدة ثم خصائص المنتج والقسمة حسب الحاجة.
استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم\(\log _{4} 3+\log _{4} x-\log _{4} y\). قم بالتبسيط، إن أمكن.
الحل:
تحتوي جميع تعبيرات السجل على نفس الأساس،\(4\).
تمت إضافة المصطلحين الأولين، لذلك نستخدم خاصية المنتج،\(\log _{a} M+\log _{a} N=\log _{a} M : N\).
نظرًا لطرح السجلات، فإننا نستخدم خاصية Quotient،\(\log _{a} M-\log _{a} N=\log _{a} \frac{M}{N}\).
استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم\(\log _{2} 5+\log _{2} x-\log _{2} y\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\log _{2} \frac{5 x}{y}\)
استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم\(\log _{3} 6-\log _{3} x-\log _{3} y\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\log _{3} \frac{6}{x y}\)
استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم\(2 \log _{3} x+4 \log _{3}(x+1)\). قم بالتبسيط، إن أمكن.
الحل:
تحتوي تعبيرات السجل على نفس الأساس،\(3\).
\(2 \log _{3} x+4 \log _{3}(x+1)\)
استخدم خاصية الطاقة،\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\).
\(\log _{3} x^{2}+\log _{3}(x+1)^{4}\)
تمت إضافة الشروط، لذلك نستخدم خاصية المنتج،\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\).
\(\log _{3} x^{2}(x+1)^{4}\)
\(2 \log _{3} x+4 \log _{3}(x+1)=\log _{3} x^{2}(x+1)^{4}\)
استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم\(3 \log _{2} x+2 \log _{2}(x-1)\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\log _{2} x^{3}(x-1)^{2}\)
استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم\(2 \log x+2 \log (x+1)\). قم بالتبسيط، إن أمكن.
- إجابة
-
\(\log x^{2}(x+1)^{2}\)
استخدم صيغة تغيير الأساس
لتقييم اللوغاريتم مع أي قاعدة أخرى، يمكننا استخدام صيغة Change-of-Base. سنظهر كيف يتم اشتقاق هذا.
\(\begin{array} {l c} {\text{Suppose we want to evaluate} \log_{a}M} & {\log_{a}M} \\ {\text{Let} \:y =\log_{a}M. }&{y=\log_{a}M} \\ {\text{Rewrite the epression in exponential form. }}&{a^{y}=M } \\ {\text{Take the }\:\log_{b} \text{of each side.}}&{\log_{b}a^{y}=\log_{b}M}\\ {\text{Use the Power Property.}}&{y\log_{b}a=\log_{b}M} \\ {\text{Solve for}\:y. }&{y=\frac{\log_{b}M}{\log_{b}a}} \\ {\text{Substiture}\:y=\log_{a}M.}&{\log_{a}M=\frac{\log_{b}M}{\log_{b}a}} \end{array}\)
تقدم صيغة تغيير القاعدة قاعدة جديدة\(b\). يمكن أن تكون هذه أي قاعدة\(b\) نريدها أين\(b>0,b≠1\). نظرًا لأن الآلات الحاسبة الخاصة بنا تحتوي على مفاتيح لقاعدة اللوغاريتمات\(10\) والقاعدة\(e\)، فسنعيد كتابة صيغة تغيير الأساس باستخدام القاعدة الجديدة كـ\(10\) أو\(e\).
صيغة تغيير القاعدة
لأي قواعد لوغاريتمية\(a, b\) و\(M>0\)،
\(\begin{array}{lll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)
عندما نستخدم الآلة الحاسبة للعثور على قيمة اللوغاريتم، فإننا عادة ما نقرّب إلى ثلاث منازل عشرية. هذا يعطينا قيمة تقريبية ولذا نستخدم الرمز المتساوي تقريبًا\((≈)\).
التقريب إلى ثلاث منازل عشرية، بشكل تقريبي\(\log _{4} 35\).
الحل:
 |
|
| استخدم صيغة تغيير الأساس. | 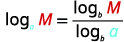 |
| تحديد\(a\) و\(M\). اختر\(10\) لـ\(b\). | 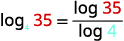 |
| أدخل التعبير\(\frac{\log 35}{\log 4}\) في الآلة الحاسبة باستخدام زر السجل للقاعدة\(10\). قرِّب حتى ثلاث منازل عشرية. | 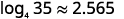 |
التقريب إلى ثلاث منازل عشرية، بشكل تقريبي\(\log _{3} 42\).
- إجابة
-
\(3.402\)
التقريب إلى ثلاث منازل عشرية، بشكل تقريبي\(\log _{5} 46\).
- إجابة
-
\(2.379\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام خصائص اللوغاريتمات.
المفاهيم الرئيسية
- \(\log _{a} 1=0 \quad \log _{a} a=1\)
- الخصائص العكسية للوغاريتمات
- من أجل\(a>0,x>0\) و\(a≠1\)
\(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)
- من أجل\(a>0,x>0\) و\(a≠1\)
- خاصية المنتج للوغاريتمات
- إذا\(M>0,N>0,a>0\)\(a≠1\)، ثم،
\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)
لوغاريتم المنتج هو مجموع اللوغاريتمات.
- إذا\(M>0,N>0,a>0\)\(a≠1\)، ثم،
- خاصية حاصل القسمة للوغاريتمات
- إذا\(M>0, N>0, \mathrm{a}>0\)\(a≠1\)، ثم،
\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)
لوغاريتم القسمة هو الفرق بين اللوغاريتمات.
- إذا\(M>0, N>0, \mathrm{a}>0\)\(a≠1\)، ثم،
- خاصية قوة اللوغاريتمات
- إذا كان\(M>0,a>0,a≠1\)\(p\) هناك أي رقم حقيقي إذن،
\(\log _{a} M^{p}=p \log _{a} M\)
سجل الرقم الذي يتم رفعه إلى طاقة هو نتاج الطاقة مضروبًا في سجل الرقم.
- إذا كان\(M>0,a>0,a≠1\)\(p\) هناك أي رقم حقيقي إذن،
- ملخص خصائص اللوغاريتمات
إذا كان\(M>0,a>0,a≠1\) أي رقم حقيقي إذن،\(p\)
| الملكية | قاعدة\(a\) | قاعدة\(e\) |
|---|---|---|
| \ (a\) ">\(\log _{a} 1=0\) | \ (e\) ">\(\ln 1=0\) | |
| \ (a\) ">\(\log _{a} a=1\) | \ (e\) ">\(\ln e=1\) | |
| الخصائص العكسية | \ (a\) ">\(a^{\log _{a} x}=x\) \(\log _{a} a^{x}=x\) |
\ (e\) ">\(e^{\ln x}=x\) \(\ln e^{x}=x\) |
| خاصية المنتج للوغاريتمات | \ (a\) ">\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) | \ (e\) ">\(\ln (M \cdot N)=\ln M+\ln N\) |
| خاصية حاصل القسمة للوغاريتمات | \ (a\) ">\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) | \ (e\) ">\(\ln \frac{M}{N}=\ln M-\ln N\) |
| خاصية قوة اللوغاريتمات | \ (a\) ">\(\log _{a} M^{p}=p \log _{a} M\) | \ (e\) ">\(\ln M^{p}=p \ln M\) |
- صيغة تغيير الأساس
لأي قواعد لوغاريتمية\(a\) و\(b\)، و\(M>0\)،\(\begin{array}{ll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)


