Skip to main content
Global

10.4E: تمارين

  1. Last updated
  2. Save as PDF
  • Page ID
    201633

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    تمارين القسم 10.3

    الممارسة تجعل من الكمال

    التمارين\(\PageIndex{21}\) Convert Between Exponential and Logarithmic Form

    في التمارين التالية، قم بالتحويل من الصورة الأسية إلى الصورة اللوغاريتمية.

    1. \(4^{2}=16\)
    2. \(2^{5}=32\)
    3. \(3^{3}=27\)
    4. \(5^{3}=125\)
    5. \(10^{3}=1000\)
    6. \(10^{-2}=\frac{1}{100}\)
    7. \(x^{\frac{1}{2}}=\sqrt{3}\)
    8. \(x^{\frac{1}{3}}=\sqrt[3]{6}\)
    9. \(32^{x}=\sqrt[4]{32}\)
    10. \(17^{x}=\sqrt[5]{17}\)
    11. \(\left(\frac{1}{4}\right)^{2}=\frac{1}{16}\)
    12. \(\left(\frac{1}{3}\right)^{4}=\frac{1}{81}\)
    13. \(3^{-2}=\frac{1}{9}\)
    14. \(4^{-3}=\frac{1}{64}\)
    15. \(e^{x}=6\)
    16. \(e^{3}=x\)
    إجابة

    2. \(\log _{2} 32=5\)

    4. \(\log _{5} 125=3\)

    6. \(\log \frac{1}{100}=-2\)

    8. \(\log _{x} \sqrt[3]{6}=\frac{1}{3}\)

    10. \(\log _{17} \sqrt[5]{17}=x\)

    12. \(\log _{\frac{1}{3}} \frac{1}{81}=4\)

    14. \(\log _{4} \frac{1}{64}=-3\)

    16. \(\ln x=3\)

    التمارين\(\PageIndex{22}\) Convert Between Exponential and Logarithmic Form

    في التمارين التالية، قم بتحويل كل معادلة لوغاريتمية إلى صورة أسية.

    1. \(3=\log _{4} 64\)
    2. \(6=\log _{2} 64\)
    3. \(4=\log _{x} 81\)
    4. \(5=\log _{x} 32\)
    5. \(0=\log _{12} 1\)
    6. \(0=\log _{7} 1\)
    7. \(1=\log _{3} 3\)
    8. \(1=\log _{9} 9\)
    9. \(-4=\log _{10} \frac{1}{10,000}\)
    10. \(3=\log _{10} 1,000\)
    11. \(5=\log _{e} x\)
    12. \(x=\log _{e} 43\)
    إجابة

    2. \(64=2^{6}\)

    4. \(32=x^{5}\)

    6. \(1=7^{0}\)

    8. \(9=9^{1}\)

    10. \(1,000=10^{3}\)

    12. \(43=e^{x}\)

    التمارين\(\PageIndex{23}\) Evaluate Logarithmic Functions

    في التمارين التالية، أوجد القيمة\(x\) في كل معادلة لوغاريتمية.

    1. \(\log _{x} 49=2\)
    2. \(\log _{x} 121=2\)
    3. \(\log _{x} 27=3\)
    4. \(\log _{x} 64=3\)
    5. \(\log _{3} x=4\)
    6. \(\log _{5} x=3\)
    7. \(\log _{2} x=-6\)
    8. \(\log _{3} x=-5\)
    9. \(\log _{\frac{1}{4}} \frac{1}{16}=x\)
    10. \(\log _{\frac{1}{3}} \frac{1}{9}=x\)
    11. \(\log _{\frac{1}{4}} 64=x\)
    12. \(\log _{\frac{1}{9}} 81=x\)
    إجابة

    2. \(x=11\)

    4. \(x=4\)

    6. \(x=125\)

    8. \(x=\frac{1}{243}\)

    10. \(x=2\)

    12. \(x=-2\)

    التمارين\(\PageIndex{24}\) Evaluate Logarithmic Functions

    في التمارين التالية، ابحث عن القيمة الدقيقة لكل لوغاريتم بدون استخدام الآلة الحاسبة.

    1. \(\log _{7} 49\)
    2. \(\log _{6} 36\)
    3. \(\log _{4} 1\)
    4. \(\log _{5} 1\)
    5. \(\log _{16} 4\)
    6. \(\log _{27} 3\)
    7. \(\log _{\frac{1}{2}} 2\)
    8. \(\log _{\frac{1}{2}} 4\)
    9. \(\log _{2} \frac{1}{16}\)
    10. \(\log _{3} \frac{1}{27}\)
    11. \(\log _{4} \frac{1}{16}\)
    12. \(\log _{9} \frac{1}{81}\)
    إجابة

    2. \(2\)

    4. \(0\)

    6. \(\frac{1}{3}\)

    8. \(-2\)

    10. \(-3\)

    12. \(-2\)

    التمارين\(\PageIndex{25}\) Graph Logarithmic Functions

    في التمارين التالية، قم برسم بياني لكل دالة لوغاريتمية.

    1. \(y=\log _{2} x\)
    2. \(y=\log _{4} x\)
    3. \(y=\log _{6} x\)
    4. \(y=\log _{7} x\)
    5. \(y=\log _{1.5} x\)
    6. \(y=\log _{2.5} x\)
    7. \(y=\log _{\frac{1}{3}} x\)
    8. \(y=\log _{\frac{1}{5}} x\)
    9. \(y=\log _{0.4} x\)
    10. \(y=\log _{0.6} x\)
    إجابة

    2.

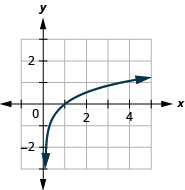
    يوضح هذا الشكل المنحنى اللوغاريتمي الذي يمر بالنقاط (1 على 4، سالب 1)، (1، 0)، (4، 1).
    الشكل 10.3.19

    4.

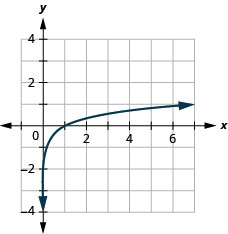
    يوضح هذا الشكل أن المنحنى اللوغاريتمي يمر بالنقاط (1 على 7، سالب 1)، (1، 0)، (7، 1).
    الشكل 10.3.20

    6.

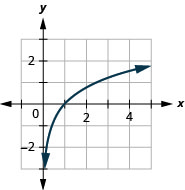
    يوضح هذا الشكل المنحنى اللوغاريتمي الذي يمر بالنقاط (2 على 5، سالب 1)، (1، 0)، (2.5، 1).
    الشكل 10.3.21

    8.

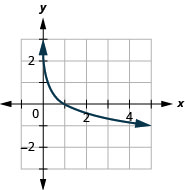
    يوضح هذا الشكل المنحنى اللوغاريتمي الذي يمر بالنقاط (1 على 5، 1)، (1، 0)، (5، سالب 1).
    الشكل 10.3.22

    10.

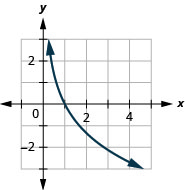
    يوضح هذا الشكل المنحنى اللوغاريتمي الذي يمر بالنقاط (3 على 5، 1)، (1، 0)، (5 فوق 3، سالب 1).
    الشكل 10.3.23
    التمارين\(\PageIndex{26}\) Solve Logarithmic Equations

    في التمارين التالية، قم بحل كل معادلة لوغاريتمية.

    1. \(\log _{a} 16=2\)
    2. \(\log _{a} 81=2\)
    3. \(\log _{a} 8=3\)
    4. \(\log _{a} 27=3\)
    5. \(\log _{a} 32=2\)
    6. \(\log _{a} 24=3\)
    7. \(\ln x=5\)
    8. \(\ln x=4\)
    9. \(\log _{2}(5 x+1)=4\)
    10. \(\log _{2}(6 x+2)=5\)
    11. \(\log _{3}(4 x-3)=2\)
    12. \(\log _{3}(5 x-4)=4\)
    13. \(\log _{4}(5 x+6)=3\)
    14. \(\log _{4}(3 x-2)=2\)
    15. \(\ln e^{4 x}=8\)
    16. \(\ln e^{2 x}=6\)
    17. \(\log x^{2}=2\)
    18. \(\log \left(x^{2}-25\right)=2\)
    19. \(\log _{2}\left(x^{2}-4\right)=5\)
    20. \(\log _{3}\left(x^{2}+2\right)=3\)
    إجابة

    2. \(a=9\)

    4. \(a=3\)

    6. \(a=\sqrt[3]{24}\)

    8. \(x=e^{4}\)

    10. \(x=5\)

    12. \(x=17\)

    14. \(x=6\)

    16. \(x=3\)

    18. \(x=-5 \sqrt{5}, x=5 \sqrt{5}\)

    20. \(x=-5, x=5\)

    التمارين\(\PageIndex{27}\) Use Logarithmic Models in Applications

    في التمارين التالية، استخدم النموذج اللوغاريتمي للحل.

    1. ما هو مستوى الديسيبل للمحادثة العادية بكثافة\(10^{−6}\) الواط لكل بوصة مربعة؟
    2. ما مستوى الديسيبل للهمس بقوة\(10^{−10}\) الواط لكل بوصة مربعة؟
    3. ما مستوى الديسيبل للضوضاء الصادرة عن دراجة نارية بقوة\(10^{−2}\) الواط لكل بوصة مربعة؟
    4. ما مستوى الديسيبل لصوت جهاز التخلص من القمامة بكثافة\(10^{−2}\) الواط لكل بوصة مربعة؟
    5. في عام 2014، شهدت تشيلي زلزالًا شديدًا بلغت قوته\(8.2\) على مقياس ريختر. في عام 2010، شهدت هايتي أيضًا زلزالًا شديدًا تم قياسه\(7.0\) على مقياس ريختر. قارن شدة الزلزالين.
    6. تشهد منطقة لوس أنجلوس العديد من الزلازل. في عام 1994، بلغت قوة زلزال نورثريدج\(6.7\) على مقياس ريختر. في عام 2014، شهدت لوس أنجلوس أيضًا زلزالًا تم قياسه\(5.1\) على مقياس ريختر. قارن شدة الزلزالين.
    إجابة

    2. يحتوي الهمس على مستوى ديسيبل\(20\) ديسيبل.

    4. يحتوي صوت التخلص من القمامة على مستوى\(100\) ديسيبل.

    6. كانت شدة زلزال نورثريدج عام 1994 في منطقة لوس أنجلوس حوالي\(40\) أضعاف شدة زلزال 2014.

    التمارين\(\PageIndex{28}\) Writing Exercises
    1. اشرح كيفية تغيير المعادلة من الصورة اللوغاريتمية إلى الصورة الأسية.
    2. اشرح الفرق بين اللوغاريتمات الشائعة واللوغاريتمات الطبيعية.
    3. اشرح لماذا\(\log _{a} a^{x}=x\).
    4. اشرح كيفية العثور\(\log _{7} 32\) على الآلة الحاسبة الخاصة بك.
    إجابة

    2. قد تختلف الإجابات

    4. قد تختلف الإجابات

    فحص ذاتي

    أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

    يحتوي هذا الجدول على أربعة صفوف وخمسة أعمدة. يقرأ الصف الأول، الذي يعمل كعنوان، «يمكنني»، «بكل ثقة، مع بعض المساعدة، والآن» لا أحصل عليه.™ يقرأ العمود الأول الموجود أسفل صف العنوان التحويل بين الصورة الأسية واللوغاريتمية، وتقييم الدوال اللوغاريتمية، والدوال اللوغاريتمية للرسم البياني، وحل المعادلات اللوغاريتمية، واستخدام النماذج اللوغاريتمية في التطبيقات. باقي الخلايا فارغة.
    الشكل 10.3.24

    ب- بعد مراجعة قائمة التحقق هذه، ماذا ستفعل لتصبح واثقًا من جميع الأهداف؟