10.3: إيجاد الدالة الأسية وتمثيلها
- Page ID
- 201615
في نهاية هذا القسم، ستكون قادرًا على:
- رسم بياني للدوال الأ
- حل المعادلات الأسية
- استخدم النماذج الأسية في التطبيقات
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بالتبسيط:\(\left(\frac{x^{3}}{x^{2}}\right)\).
إذا فاتتك هذه المشكلة، راجع المثال 5.13. - تقييم: أ.\(2^{0}\) ب\(\left(\frac{1}{3}\right)^{0}\).
إذا فاتتك هذه المشكلة، راجع المثال 5.14. - تقييم: أ.\(2^{−1}\) ب\(\left(\frac{1}{3}\right)^{-1}\).
إذا فاتتك هذه المشكلة، راجع المثال 5.15.
رسم بياني للدوال الأ
لا تعطينا الوظائف التي درسناها حتى الآن نموذجًا للعديد من الظواهر التي تحدث بشكل طبيعي. من نمو السكان وانتشار الفيروسات إلى التحلل الإشعاعي والاهتمام المركب، تختلف النماذج تمامًا عما درسناه حتى الآن. تتضمن هذه النماذج دوال أسية.
الدالة الأسية هي دالة في الشكل\(f(x)=a^{x}\) حيث\(a>0\) و\(a≠1\).
الدالة الأسية، حيث\(a>0\) و\(a≠1\)، هي دالة في الشكل
\(f(x)=a^{x}\)
لاحظ أن المتغير في هذه الدالة هو الأس. في وظائفنا حتى الآن، كانت المتغيرات هي الأساس.

يقول تعريفنا\(a≠1\). إذا سمحنا بذلك\(a=1\)،\(f(x)=a^{x}\) يصبح\(f(x)=1^{x}\). لأنه\(1^{x}=1\) بالنسبة لجميع الأرقام الحقيقية،\(f(x)=1\). هذه هي الوظيفة الثابتة.
يقول تعريفنا أيضًا\(a>0\). إذا تركنا القاعدة سالبة، على سبيل المثال\(−4\)،\(f(x)=(−4)^{x}\) فهذا ليس رقمًا حقيقيًا عندما\(x=\frac{1}{2}\).
\(\begin{aligned} f(x) &=(-4)^{x} \\ f\left(\frac{1}{2}\right) &=(-4)^{\frac{1}{2}} \\ f\left(\frac{1}{2}\right) &=\sqrt{-4} \text { not a real number } \end{aligned}\)
في الواقع،\(f(x)=(−4)^{x}\) لن يكون عددًا حقيقيًا في أي وقت\(x\) هو كسر بمقام زوجي. لذلك يتطلب تعريفنا\(a>0\).
من خلال تمثيل بعض الدوال الأسية بيانيًّا، سنتمكن من رؤية خصائصها الفريدة.
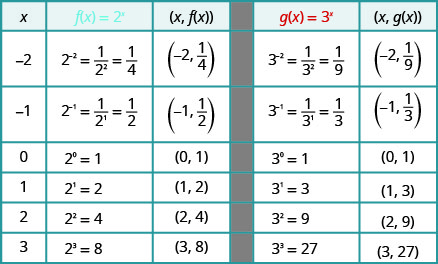
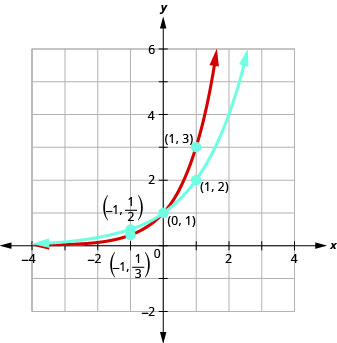
على نفس الرسم البياني لنظام الإحداثيات\(f(x)=2^{x}\) و\(g(x)=3^{x}\).
الحل:
سنستخدم التخطيط النقطي لرسم الوظائف.
رسم بياني:\(f(x)=4^{x}\).
- إجابة
-
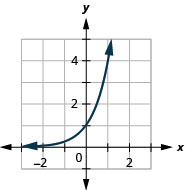
الشكل 10.2.4
رسم بياني:\(g(x)=5^{x}\)
- إجابة
-
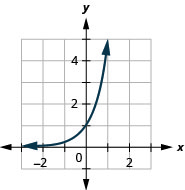
الشكل 10.2.5
إذا نظرنا إلى الرسوم البيانية من المثال السابق 10.2.1 والتمارين 10.2.1 و 10.2.2، يمكننا تحديد بعض خصائص الدوال الأسية.
تحتوي جميع الرسوم البيانية لـ\(f(x)=2^{x}\) و\(g(x)=3^{x}\)، بالإضافة إلى الرسوم البيانية لـ\(f(x)=4^{x}\) و\(g(x)=5^{x}\)، على نفس الشكل الأساسي. هذا هو الشكل الذي نتوقعه من دالة أسية حيث\(a>1\).
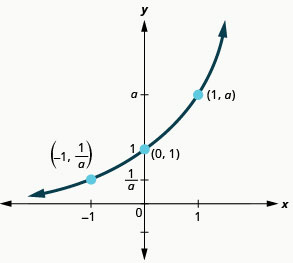
نلاحظ أنه بالنسبة لكل دالة، يحتوي الرسم البياني على النقطة\((0,1)\). هذا منطقي لأنه\(a^{0}=1\) بالنسبة لأي شخص\(a\).
يحتوي الرسم البياني لكل دالة\(f(x)=a^{x}\) أيضًا على النقطة\((1,a)\). الرسم البياني\(f(x)=2^{x}\) الوارد\((1,2)\) والرسم البياني\(g(x)=3^{x}\) الوارد\((1,3)\). هذا منطقي مثل\(a^{1}=a\).
لاحظ أيضًا أن الرسم البياني لكل دالة يحتوي\(f(x)=a^{x}\) أيضًا على النقطة\((−1,\frac{1}{a})\). الرسم البياني\(f(x)=2^{x}\) الوارد\((−1,\frac{1}{2})\) والرسم البياني\(g(x)=3^{x}\) المتضمن\((−1,\frac{1}{3})\). هذا منطقي مثل\(a^{−1}=\frac{1}{a}\).
ما مجال كل وظيفة؟ من الرسوم البيانية يمكننا أن نرى أن المجال هو مجموعة جميع الأرقام الحقيقية. لا توجد قيود على المجال. نكتب المجال بالتدوين الفاصل الزمني كـ\((−∞,∞)\).
انظر إلى كل رسم بياني. ما نطاق الدالة؟ لا يصل الرسم البياني أبدًا إلى\(x\) المحور -. النطاق هو جميع الأرقام الإيجابية. نكتب النطاق في الترميز الفاصل الزمني كـ\((0,∞)\).
عندما يقترب رسم بياني لدالة من خط مستقيم ولكن لا يلمسه أبدًا، فإننا نسمي هذا الخط بخط التقارب. بالنسبة للدوال الأسية التي ننظر إليها، يقترب الرسم البياني من\(x\) المحور السيني بشكل وثيق جدًا ولكنه لن يعبره أبدًا، ونطلق على الخط\(y=0\) المستقيم،\(x\) المحور السيني، خط التقارب الأفقي.
خصائص الرسم البياني\(f(x)=a^{x}\) للوقت\(a>1\)
| اسم النطاق | \((-\infty, \infty)\) |
| النطاق | \((0, \infty)\) |
| \(x\)-اعتراض | لا شيء |
| \(y\)-اعتراض | \((0,1)\) |
| يحتوي على | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| خط التقارب | \(x\)-المحور، الخط\(y=0\) |
\(f(x)=a^{x}\)يقول تعريفنا للدالة الأسية\(a>0\)، لكن الأمثلة والمناقشة حتى الآن كانت حول الدوال أين\(a>1\). ماذا يحدث عندما\(0<a<1\) يستكشف المثال التالي هذا الاحتمال.
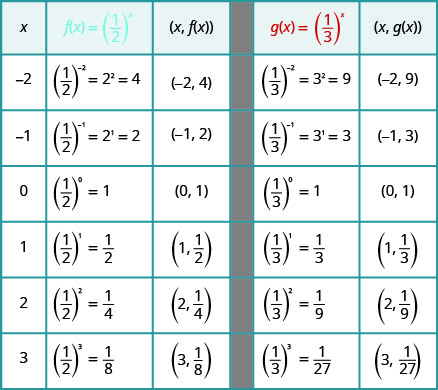
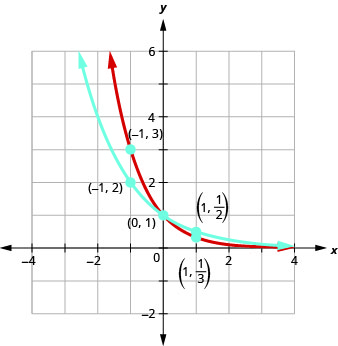
على نفس نظام الإحداثيات، الرسم البياني\(f(x)=\left(\frac{1}{2}\right)^{x}\) و\(g(x)=\left(\frac{1}{3}\right)^{x}\).
الحل:
سنستخدم التخطيط النقطي لرسم الوظائف.
رسم بياني:\(f(x)=\left(\frac{1}{4}\right)^{x}\).
- إجابة
-
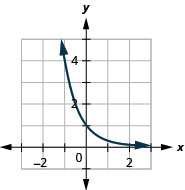
الشكل 10.2.9
رسم بياني:\(g(x)=\left(\frac{1}{5}\right)^{x}\).
- إجابة
-
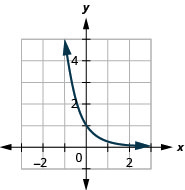
الشكل 10.2.10
الآن دعونا ننظر إلى الرسوم البيانية من المثال السابق 10.2.2 والتمارين 10.2.3 و 10.2.4 حتى نتمكن الآن من تحديد بعض خصائص الدوال الأسية حيث\(0<a<1\).
تحتوي الرسوم البيانية\(g(x)=\left(\frac{1}{3}\right)^{x}\) وكذلك الرسوم البيانية الخاصة\(g(x)=\left(\frac{1}{5}\right)^{x}\) بكل\(f(x)=\left(\frac{1}{4}\right)^{x}\) منها على نفس الشكل الأساسي.\(f(x)=\left(\frac{1}{2}\right)^{x}\) في حين أن هذا هو الشكل الذي نتوقعه من دالة أسية حيث\(0<a<1\) تنخفض الرسوم البيانية من اليسار إلى اليمين بينما تتحرك الرسوم البيانية السابقة\(a>1\)، عندما، من الأعلى من اليسار إلى اليمين.
نلاحظ أنه بالنسبة لكل دالة، لا يزال الرسم البياني يحتوي على النقطة\((0, 1)\). هذا منطقي لأنه\(a^{0}=1\) بالنسبة لأي شخص\(a\).
كما كان من قبل، يحتوي الرسم البياني لكل دالة أيضًا على النقطة\((1,a)\).\(f(x)=a^{x}\) الرسم البياني\(f(x)=\left(\frac{1}{2}\right)^{x}\) الوارد\(\left(1, \frac{1}{2}\right)\) والرسم البياني\(g(x)=\left(\frac{1}{3}\right)^{x}\) الوارد\(\left(1, \frac{1}{3}\right)\). هذا منطقي مثل\(a^{1}=a\).
لاحظ أيضًا أن الرسم البياني لكل دالة\(f(x)=a^{x}\)، يحتوي أيضًا على النقطة\(\left(-1, \frac{1}{a}\right)\). الرسم البياني\(f(x)=\left(\frac{1}{2}\right)^{x}\) الوارد\((−1,2)\) والرسم البياني\(g(x)=\left(\frac{1}{3}\right)^{x}\) الوارد\((−1,3)\). هذا منطقي مثل\(a^{-1}=\frac{1}{a}\).
ما المجال والنطاق لكل وظيفة؟ من الرسوم البيانية يمكننا أن نرى أن المجال هو مجموعة جميع الأرقام الحقيقية ونكتب المجال بالتدوين الفاصل الزمني كـ\((−∞,∞)\). مرة أخرى، لا يصل الرسم البياني أبدًا إلى\(x\) المحور -. النطاق هو جميع الأرقام الإيجابية. نكتب النطاق في الترميز الفاصل الزمني كـ\((0,∞)\).
سنلخص هذه الخصائص في الرسم البياني أدناه. والتي تشمل أيضًا متى\(a>1\).
خصائص الرسم البياني لـ\(f(x)=a^{x}\)
| عندما\(a>1\) | عندما\(0<a<1\) | ||
|---|---|---|---|
| \ («>1\)" >المجال | \((-\infty, \infty)\) | \ (0<a<1\) ">المجال | \((-\infty, \infty)\) |
| \ («>1\)" >النطاق | \((0, \infty)\) | \ (0 <a <1\) ">النطاق | \((0, \infty)\) |
| \ («>1\)" >\(x\) - الاعتراض | لا شيء | \ (0<a <1\) ">\(x\) -التقاطع | لا شيء |
| \ («>1\)" >\(y\) - الاعتراض | \((0,1)\) | \ (0<a <1\) ">\(y\) -التقاطع | \((0,1)\) |
| \ («>1\)" >يحتوي على | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1\) ">يحتوي على | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ («>1\)" >التقارب |
\(x\)-المحور، الخط\(y=0\) |
\ (0 <a <1\) ">خط التقارب | \(x\)-المحور، الخط\(y=0\) |
| \ («>1\)" >الشكل الأساسي | زيادة | \ (0<a<1\) ">الشكل الأساسي | تناقص |
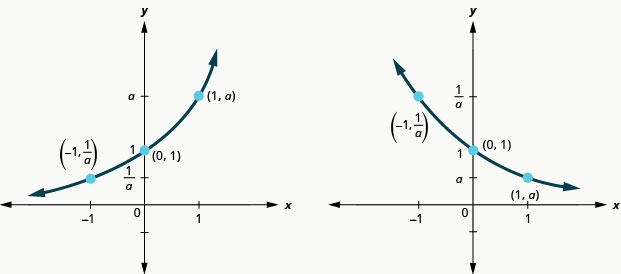
من المهم بالنسبة لنا أن نلاحظ أن كلا من هذه الرسوم البيانية فردية، حيث يجتاز كلاهما اختبار الخط الأفقي. هذا يعني أن الدالة الأسية سيكون لها معكوس. سننظر إلى هذا لاحقًا.
عندما قمنا برسم الدوال التربيعية بيانيًا، كنا قادرين على الرسم البياني باستخدام الترجمة بدلاً من مجرد رسم النقاط. هل سيعمل ذلك في تمثيل الدوال الأسية بيانيًّا؟
على نفس الرسم البياني لنظام الإحداثيات\(f(x)=2^{x}\) و\(g(x)=2^{x+1}\).
الحل:
سنستخدم التخطيط النقطي لرسم الوظائف.

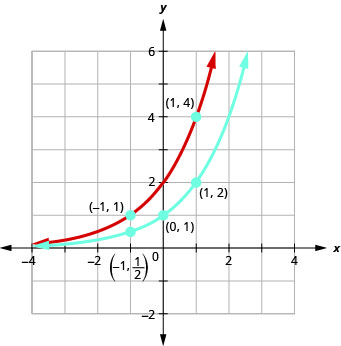
على نفس نظام الإحداثيات، الرسم البياني:\(f(x)=2^{x}\) و\(g(x)=2^{x-1}\).
- إجابة
-
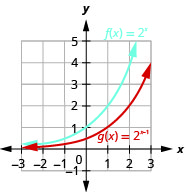
الشكل 10.2.14
على نفس نظام الإحداثيات، الرسم البياني\(f(x)=3^{x}\) و\(g(x)=3^{x+1}\).
- إجابة
-
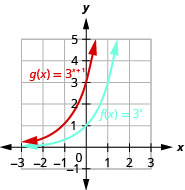
الشكل 10.2.15
بالنظر إلى الرسوم البيانية للوظائف\(f(x)=2^{x}\)\(g(x)=2^{x+1}\) وفي المثال الأخير، نرى أن إضافة واحدة في الأس تسببت في تحول أفقي لوحدة واحدة إلى اليسار. يتيح لنا التعرف على هذا النمط رسم وظائف أخرى بنفس النمط عن طريق الترجمة.
لننظر الآن في موقف آخر يمكن رسمه بسهولة أكبر عن طريق الترجمة، بمجرد أن نتعرف على النمط.
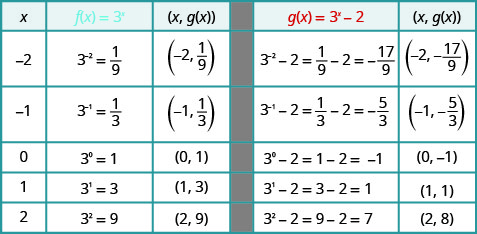
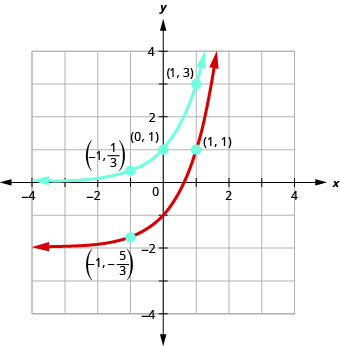
على نفس الرسم البياني لنظام الإحداثيات\(f(x)=3^{x}\) و\(g(x)=3^{x}-2\).
الحل:
سنستخدم التخطيط النقطي لرسم الوظائف.
على نفس نظام الإحداثيات، الرسم البياني\(f(x)=3^{x}\) و\(g(x)=3^{x}+2\).
- إجابة
-
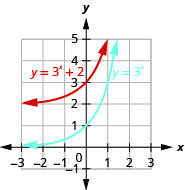
الشكل 10.2.18
على نفس نظام الإحداثيات، الرسم البياني\(f(x)=4^{x}\) و\(g(x)=4^{x}-2\).
- إجابة
-
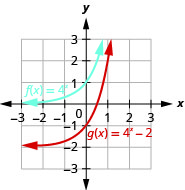
الشكل 10.2.19
بالنظر إلى الرسوم البيانية للدوال\(f(x)=3^{x}\)\(g(x)=3^{x}−2\) وفي المثال الأخير، نرى أن الطرح\(2\) تسبب في حدوث تحول عمودي لوحدتين. لاحظ أن خطوط التقارب الأفقية تحولت أيضًا إلى\(2\) وحدات لأسفل. يتيح لنا التعرف على هذا النمط رسم وظائف أخرى بنفس النمط عن طريق الترجمة.
تحتوي جميع دالاتنا الأسية إما على عدد صحيح أو رقم نسبي كأساس. سننظر الآن إلى دالة أسية بعدد غير نسبي كأساس.
قبل أن نتمكن من النظر إلى هذه الدالة الأسية، نحتاج إلى تحديد العدد غير النسبي،\(e\). يتم استخدام هذا الرقم كأساس في العديد من التطبيقات في العلوم والأعمال التي تم تصميمها بواسطة الدوال الأسية. يتم تعريف الرقم على أنه قيمة\(\left(1+\frac{1}{n}\right)^{n}\) as\(n\) تصبح أكبر وأكبر. نقول، عندما نقترب\(n\) من اللانهاية، أو يزداد بلا حدود. يعرض الجدول قيمة عدة قيم\(\left(1+\frac{1}{n}\right)^{n}\) لـ\(n\).
| \(n\) | \(\left(1+\frac{1}{n}\right)^{n}\) |
|---|---|
| \ (n\) ">\(1\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2\) |
| \ (n\) ">\(2\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.25\) |
| \ (n\) ">\(5\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.48832\) |
| \ (n\) ">\(10\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.59374246\) |
| \ (n\) ">\(100\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.704813829 \ldots\) |
| \ (n\) ">\(1,000\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.716923932 \ldots\) |
| \ (n\) ">\(10,000\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.718145927 \ldots\) |
| \ (n\) ">\(100,000\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.718268237 \ldots\) |
| \ (n\) ">\(1,000,000\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.718280469 \ldots\) |
| \ (n\) ">\(1,000,000,000\) | \ (\ يسار (1+\ فراك {1} {n}\ يمين) ^ {n}\) ">\(2.718281827 \ldots\) |
\(e \approx 2.718281827\)
الرقم\(e\) يشبه الرقم\(π\) في أننا نستخدم رمزًا لتمثيله لأن تمثيله العشري لا يتوقف أو يتكرر أبدًا. الرقم غير العقلاني\(e\) يسمى القاعدة الطبيعية.
قاعدة طبيعية\(e\)
\(e\)يتم تعريف الرقم على أنه قيمة\(\left(1+\frac{1}{n}\right)^{n}\)،\(n\) كزيادات بدون قيود. نقول، مع\(n\) اقتراب اللانهاية،
\(e \approx 2.718281827\)
تسمى الدالة الأسية التي قاعدتها الدالة الأسية الطبيعية.\(e\)\(f(x)=e^{x}\)
دالة أسية طبيعية
الدالة الأسية الطبيعية هي دالة أسية قاعدتها\(e\)
\(f(x)=e^{x}\)
المجال هو\((−∞,∞)\) والنطاق هو\((0,∞)\).
دعونا نرسم الدالة\(f(x)=e^{x}\) على نفس نظام الإحداثيات مثل\(g(x)=2^{x}\) و\(h(x)=3^{x}\).
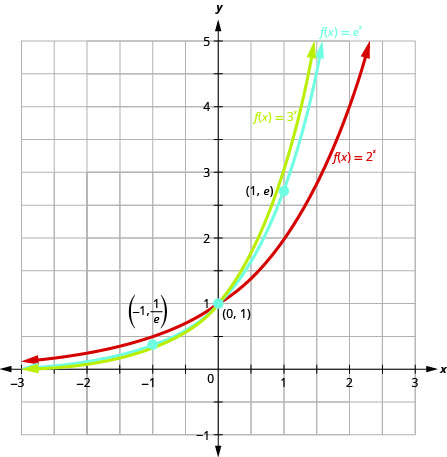
لاحظ أن الرسم البياني\(f(x)=e^{x}\) هو «بين» الرسوم البيانية لـ\(g(x)=2^{x}\) و\(h(x)=3^{x}\). هل هذا منطقي\(2<e<3\)؟
حل المعادلات الأسية
\(a^{x}\)تُسمى المعادلات التي تتضمن تعبيرًا أسيًا المعادلات الأسية. لحلها، نستخدم خاصية تقول «طالما\(a≠1\)،\(a>0\) وإذا كان الأمر كذلك،\(a^{x}=a^{y}\) فهذا صحيح»\(x=y\). بعبارة أخرى، في المعادلة الأسية، إذا كانت القواعد متساوية، فإن الأسس تكون متساوية.
خاصية واحد لواحد للمعادلات الأسية
من أجل\(a>0\) و\(a≠1\)،
إذا\(a^{x}=a^{y}\)، إذن\(x=y\).
لاستخدام هذه الخاصية، يجب أن نتأكد من كتابة طرفي المعادلة بنفس القاعدة.
حل:\(3^{2 x-5}=27\).
الحل:
| الخطوة 1: اكتب كلا طرفي المعادلة بنفس القاعدة. | نظرًا لأن الجانب الأيسر يحتوي على قاعدة\(3\)، فإننا نكتب الجانب الأيمن بالقاعدة\(3\). \(27=3^{3}\) | \(3^{2 x-5}=27\) \(3^{2 x-5}=3^{3}\) |
| الخطوة 2: اكتب معادلة جديدة عن طريق ضبط الأسس متساوية. | نظرًا لأن القواعد هي نفسها، يجب أن تكون الأسس متساوية. | \(2x-5=3\) |
| الخطوة 3: حل المعادلة. |
أضف\(5\) إلى كل جانب. اقسم على\(2\). |
\(\begin{aligned} 2 x &=8 \\ x &=4 \end{aligned}\) |
| الخطوة 4: تحقق من الحل. | استبدل\(x=4\) المعادلة الأصلية. | \(\begin{aligned} 3^{2 x-5} &=27 \\ 3^{2 \cdot \color{red}{4}\color{black}{-}5} & \stackrel{?}{=} 27 \\ 3^{3} &\stackrel{?}{=}27 \\ 27 &=27 \end{aligned}\) |
حل:\(3^{3 x-2}=81\).
- إجابة
-
\(x=2\)
حل:\(7^{x-3}=7\).
- إجابة
-
\(x=4\)
يتم تلخيص الخطوات أدناه.
كيفية حل دالة أسية
- اكتب كلا طرفي المعادلة بنفس القاعدة، إن أمكن.
- اكتب معادلة جديدة بتعيين الأسس متساوية.
- حل المعادلة.
- تحقق من الحل.
في المثال التالي، سنستخدم خصائصنا على الأسس.
حل\(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\).
الحل:
| \(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\) | |
| استخدم خاصية الأسس:\(\frac{a^{m}}{a^{n}}=a^{m-n}\). | \(e^{x^{2}-3}=e^{2 x}\) |
| اكتب معادلة جديدة بتعيين الأسس متساوية. | \(x^{2}-3=2 x\) |
| حل المعادلة. | \(x^{2}-2 x-3=0\) |
| \((x-3)(x+1)=0\) | |
| \(x=3, x=-1\) | |
| تحقق من الحلول. | |
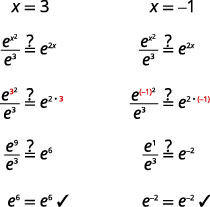 |
حل:\(\frac{e^{x^{2}}}{e^{x}}=e^{2}\).
- إجابة
-
\(x=-1, x=2\)
حل:\(\frac{e^{x^{2}}}{e^{x}}=e^{6}\).
- إجابة
-
\(x=-2, x=3\)
استخدم النماذج الأسية في التطبيقات
تمثل الدوال الأسية العديد من المواقف. إذا كنت تمتلك حسابًا مصرفيًا، فقد اختبرت استخدام دالة أسية. هناك صيغتان تستخدمان لتحديد الرصيد في الحساب عند كسب الفائدة. إذا تم استثمار رأس المال بسعر فائدة\(r\)\(A\)، فسيعتمد الرصيد الجديد\(t\) لسنوات على عدد المرات التي يتم فيها مضاعفة الفائدة.\(P\) إذا كانت الفائدة تتضاعف\(n\) مرات في السنة، فإننا نستخدم الصيغة\(A=P\left(1+\frac{r}{n}\right)^{n t}\). إذا كانت الفائدة تتضاعف باستمرار، فإننا نستخدم الصيغة\(A=Pe^{rt}\). هذه هي صيغ الفائدة المركبة.
الفائدة المركبة
بالنسبة لرأس المال المستثمر بسعر فائدة\(r\)،\(t\) لسنوات، فإن الرصيد الجديد هو:\(P\)\(A\)
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\)
أثناء العمل مع صيغ الاهتمام، غالبًا ما يكون من المفيد تحديد قيم المتغيرات أولاً ثم استبدالها في الصيغة.
\(10,000\)تم استثمار ما مجموعه $ في صندوق جامعي لحفيد جديد. إذا كان معدل الفائدة هو\(5\)%، فكم سيكون في الحساب\(18\) بالسنوات حسب كل طريقة من طرق التجميع؟
- مجمع ربع سنوي
- مجمع شهري
- مركب بشكل مستمر
الحل:
حدد قيم كل متغير في الصيغ. تذكر أن تعبر عن النسبة المئوية في صورة عدد عشري.
\(\begin{aligned} A &=? \\ P &=\$ 10,000 \\ r &=0.05 \\ t &=18 \text { years } \end{aligned}\)
أ- للتركيب الفصلي،\(n=4\). هناك\(4\) أرباع في السنة.
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
استبدل القيم في الصيغة.
\(A=10,000\left(1+\frac{0.05}{4}\right)^{4 \cdot 18}\)
احسب المبلغ. احرص على مراعاة ترتيب العمليات عند إدخال التعبير في الآلة الحاسبة.
\(A=\$ 24,459.20\)
ب- للتركيب الشهري،\(n=12\) .هناك\(12\) أشهر في السنة.
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
استبدل القيم في الصيغة.
\(A=10,000\left(1+\frac{0.05}{12}\right)^{12 \cdot 18}\)
احسب المبلغ.
\(A=\$ 24,550.08\)
ج. للتركيب المستمر،
\(A=P e^{r t}\)
استبدل القيم في الصيغة.
\(A=10,000 e^{0.05 \cdot 18}\)
احسب المبلغ.
\(A=\$ 24,596.03\)
استثمرت أنجيلا $\(15,000\) في حساب التوفير. إذا كان معدل الفائدة هو\(4\)%، فكم سيكون في الحساب\(10\) بالسنوات حسب كل طريقة من طرق التجميع؟
- مجمع ربع سنوي
- مجمع شهري
- مركب بشكل مستمر
- إجابة
-
- $\(22,332.96\)
- $\(22,362.49\)
- $\(22,377.37\)
استثمر آلان $\(10,000\) في صندوق مشترك. إذا كان معدل الفائدة هو\(5\)%، فكم سيكون في الحساب\(15\) بالسنوات حسب كل طريقة من طرق التجميع؟
- مجمع ربع سنوي
- مجمع شهري
- مركب بشكل مستمر
- إجابة
-
- $\(21,071.81\)
- $\(21,137.04\)
- $\(21,170.00\)
تتضمن الموضوعات الأخرى التي تم تصميمها بواسطة الدوال الأسية النمو والانحلال. يستخدم كلاهما أيضًا الصيغة التي\(A=Pe^{rt}\) استخدمناها لنمو الأموال. بالنسبة للنمو والانحلال، نستخدم عمومًا\(A_{0}\)، كمبلغ أصلي بدلاً من تسميته\(P\)، رأس المال. نرى أن النمو الأسي له معدل نمو إيجابي وأن الاضمحلال الأسي له معدل نمو سلبي.
النمو المتسارع والانحلال
بالنسبة للمبلغ الأصلي\(A_{0}\)، الذي ينمو أو يتحلل بمعدل\(r\)، لفترة معينة\(t\)\(A\)، يكون المبلغ النهائي:
\(A=A_{0} e^{r t}\)
عادة ما يظهر النمو المتسارع في نمو أعداد البشر أو الحيوانات أو البكتيريا. يبحث مثالنا التالي في نمو الفيروس.
كريس هو باحث في مركز السيطرة على الأمراض والوقاية منها ويحاول فهم سلوك فيروس جديد وخطير. يبدأ تجربته مع\(100\) الفيروس الذي ينمو بمعدل\(25\)% في الساعة. سيتحقق من الفيروس في\(24\) غضون ساعات. كم عدد الفيروسات التي سيجدها؟
الحل:
حدد قيم كل متغير في الصيغ. تأكد من وضع النسبة المئوية في شكل عشري. تأكد من تطابق الوحدات - السعر لكل ساعة والوقت بالساعات.
\(\begin{aligned} A &=? \\ A_{0} &=100 \\ r &=0.25 / \text { hour } \\ t &=24 \text { hours } \end{aligned}\)
استبدل القيم في الصيغة:\(A=A_{0} e^{r t}\).
\(A=100 e^{0.25 \cdot 24}\)
احسب المبلغ.
\(A=40,342.88\)
انتقل إلى أقرب فيروس كامل.
\(A=40,343\)
سيجد الباحث\(40,343\) الفيروسات.
تدرس باحثة أخرى في مركز السيطرة على الأمراض والوقاية منها، ليزا، نمو البكتيريا. تبدأ تجربته مع\(50\) البكتيريا التي تنمو بمعدل\(15\)% في الساعة. سوف يفحص البكتيريا كل\(8\) ساعة. كم عدد البكتيريا التي سيجدها في\(8\) ساعات؟
- إجابة
-
سوف تجد\(166\) البكتيريا.
ماريا، عالمة الأحياء، تراقب نمط نمو الفيروس. تبدأ بالفيروس\(100\) الذي ينمو بمعدل\(10\)% في الساعة. ستتحقق من الفيروس في\(24\) غضون ساعات. كم عدد الفيروسات التي ستعثر عليها؟
- إجابة
-
سوف تجد\(1,102\) الفيروسات.
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية في تقييم الوظائف الأسية ورسمها بيانيًا.
المفاهيم الرئيسية
- خصائص الرسم البياني لـ\(f(x)=a^{x}\):
| عندما\(a>1\) | عندما\(0<a<1\) | ||
|---|---|---|---|
| \ («>1\)" >المجال | \((-\infty, \infty)\) | \ (0<a<1\) ">المجال | \((-\infty, \infty)\) |
| \ («>1\)" >النطاق | \((0, \infty)\) | \ (0 <a <1\) ">النطاق | \((0, \infty)\) |
| \ («>1\)" >\(x\) - الاعتراض | لا شيء | \ (0<a <1\) ">\(x\) -التقاطع | لا شيء |
| \ («>1\)" >\(y\) - الاعتراض | \((0,1)\) | \ (0<a <1\) ">\(y\) -التقاطع | \((0,1)\) |
| \ («>1\)" >يحتوي على | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1\) ">يحتوي على | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ («>1\)" >التقارب |
\(x\)-المحور، الخط\(y=0\) |
\ (0 <a <1\) ">خط التقارب | \(x\)-المحور، الخط\(y=0\) |
| \ («>1\)" >الشكل الأساسي | زيادة | \ (0<a<1\) ">الشكل الأساسي | تناقص |
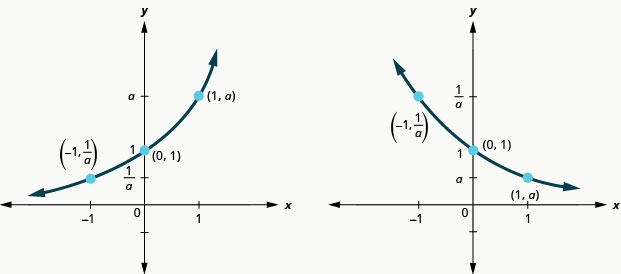
- خاصية واحد لواحد للمعادلات الأسية:
لـ\(a>0\) و\(a≠1\)،\(A=A_{0} e^{r t}\)
- كيفية حل المعادلة الأسية
- اكتب كلا طرفي المعادلة بنفس القاعدة، إن أمكن.
- اكتب معادلة جديدة بتعيين الأسس متساوية.
- حل المعادلة.
- تحقق من الحل.
- الفائدة المركبة: بالنسبة لرأس\(P\) المال المستثمر بسعر فائدة\(r\)،\(t\) لسنوات، فإن الرصيد الجديد هو\(A\)
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\) - النمو المتسارع والانحلال: بالنسبة للكمية الأصلية\(A_{0}\) التي تنمو أو تتحلل بمعدل\(r\)، لفترة معينة\(t\)، يكون المقدار النهائي،\(A\)، هو\(A=A_{0}e^{rt}\).
مسرد المصطلحات
- خط التقارب
- الخط الذي يقترب منه رسم بياني للدالة عن كثب ولكن لا يلمسه أبدًا.
- دالة أسية
- الدالة الأسية، حيث\(a>0\) و\(a≠1\)، هي دالة في الشكل\(f(x)=a^{x}\).
- قاعدة طبيعية
- \(e\)يتم تعريف الرقم على أنه قيمة\((1+\frac{1}{n})^{n}\)، حيث\(n\) تصبح أكبر وأكبر. نقول، كلما\(n\) زاد بلا قيود،\(e≈2.718281827...\)
- دالة أسية طبيعية
- الدالة الأسية الطبيعية هي دالة أسية أساسها\(e\):\(f(x)=e^{x}\). المجال هو\((−∞,∞)\) والنطاق هو\((0,∞)\).


