10.2: إيجاد الدوال المركبة والعكسية
- Page ID
- 201595
في نهاية هذا القسم، ستكون قادرًا على:
- البحث عن الدوال المركبة وتقييمها
- حدد ما إذا كانت الدالة واحدة إلى واحدة
- أوجد معكوس الدالة
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- إذا كان\(f(x)=2 x-3\) الأمر كذلك\(g(x)=x^{2}+2 x-3\)، فابحث\(f(4)\).
إذا فاتتك هذه المشكلة، راجع المثال 3.48. - حل لـ\(x\)،\(3x+2y=12\).
إذا فاتتك هذه المشكلة، راجع المثال 2.31. - قم بالتبسيط:\(5 \frac{(x+4)}{5}-4\).
إذا فاتتك هذه المشكلة، راجع مثال 1.25.
في هذا الفصل، سوف نقدم نوعين جديدين من الدوال، الدوال الأسية والدوال اللوغاريتمية. تستخدم هذه الوظائف على نطاق واسع في الأعمال والعلوم كما سنرى.
البحث عن الدوال المركَّبة وتقييمها
قبل تقديم الوظائف، نحتاج إلى إلقاء نظرة على عملية أخرى تتعلق بوظائف تسمى التكوين. في التكوين، يكون ناتج إحدى الوظائف هو إدخال دالة ثانية. بالنسبة للوظائف\(f\) و\(g\)، تتم كتابة التكوين\(f∘g\) ويتم تحديده بواسطة\((f∘g)(x)=f(g(x))\).
نقرأ\(f(g(x))\) كـ «\(f\)\(g\)من»\(x\).
للقيام بالتكوين، يصبح ناتج الدالة الأولى\(g(x)\)، هو مدخل الوظيفة الثانية\(f\)، ولذا يجب أن نتأكد من أنها جزء من مجال\(f\).
يتم كتابة تكوين الوظائف\(f\)\(g\)\(f \cdot g\) ويتم تعريفه بواسطة
\((f \circ g)(x)=f(g(x))\)
نقرأ\(f(g(x))\) اعتبارًا\(f\)\(g\) من\(x\).
لقد استخدمنا بالفعل التركيب دون استخدام الترميز عدة مرات من قبل. عندما قمنا برسم الدوال التربيعية باستخدام الترجمات، كنا نؤلف الدوال. على سبيل المثال، إذا قمنا أولاً\(g(x)=x^{2}\) بالرسم البياني في صورة مكافئ ثم نقلناه رأسيًا لأربع وحدات، فإننا نستخدم التركيبة المحددة\((f∘g)(x)=f(g(x))\) بالمكان\(f(x)=x−4\).
للوظائف\(f(x)=4x-5\) وابحث\(g(x)=2x+3\)
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
الحل:
-
استخدم تعريف\((f \circ g)(x)\). 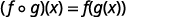

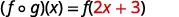

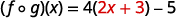
قم بالتوزيع. 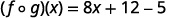
قم بالتبسيط. 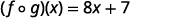
الجدول 10-1-1 -
استخدم تعريف\((f \circ g)(x)\). 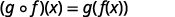

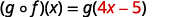

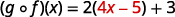
قم بالتوزيع. 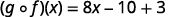
قم بالتبسيط. 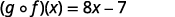
الجدول 10-1-2
لاحظ الفرق في النتيجة في الجزء أ. والجزء ب.
ج- لاحظ أن\((f \cdot g)(x)\) هذا مختلف عن\((f \circ g)(x)\). في الجزء أ. قمنا بتكوين الوظائف. الآن في الجزء ج. نحن لا نؤلفها، بل نضربها.
استخدم تعريف\((f \cdot g)(x)\).
\((f \cdot g)(x)=f(x) \cdot g(x)\)
بديل\(f(x)=4 x-5\) و\(g(x)=2 x+3\).
\((f \cdot g)(x)=(4 x-5) \cdot(2 x+3)\)
اضرب.
\((f \cdot g)(x)=8 x^{2}+2 x-15\)
للوظائف\(f(x)=3x-2\) وابحث\(g(x)=5x+1\)
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- إجابة
-
- \(15x+1\)
- \(15x-9\)
- \(15 x^{2}-7 x-2\)
للوظائف\(f(x)=4 x-3\)\(g(x)=6x-5\)، وابحث
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- إجابة
-
- \(24 x-23\)
- \(24 x-23\)
- \(24 x^{2}-38 x+15\)
في المثال التالي، سنقوم بتقييم تركيبة لقيمة محددة.
للوظائف\(f(x)=x^{2}-4\)\(g(x)=3 x+2\)، وابحث عن:
- \((f \circ g)(-3)\)
- \((g \circ f)(-1)\)
- \((f \circ f)(2)\)
الحل:
-
استخدم تعريف\((f \circ g)(-3)\). 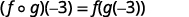

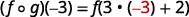
قم بالتبسيط. 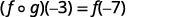

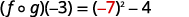
قم بالتبسيط. 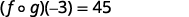
الجدول 10-1-3 -
استخدم تعريف\((g \circ f)(-1)\). 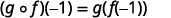

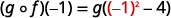
قم بالتبسيط. 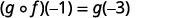

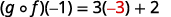
قم بالتبسيط. 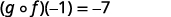
الجدول 10-1-4 -
استخدم تعريف\((f \circ f)(2)\). 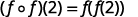

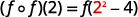
قم بالتبسيط. 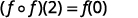

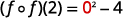
قم بالتبسيط. 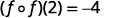
الجدول 10-1-5
للوظائف\(f(x)=x^{2}-9\)\(g(x)=2x+5\)، وابحث
- \((f \circ g)(-2)\)
- \((g \circ f)(-3)\)
- \((f \circ f)(4)\)
- إجابة
-
- \(-8\)
- \(5\)
- \(40\)
للوظائف\(f(x)=x^{2}+1\)\(g(x)=3x-5\)، وابحث
- \((f \circ g)(-1)\)
- \((g \circ f)(2)\)
- \((f \circ f)(-1)\)
- إجابة
-
- \(65\)
- \(10\)
- \(5\)
حدِّد ما إذا كانت الدالة واحدة إلى واحدة
عندما قدمنا الوظائف لأول مرة، قلنا أن الوظيفة هي علاقة تخصص لكل عنصر في مجاله عنصرًا واحدًا بالضبط في النطاق. بالنسبة لكل زوج مرتب في العلاقة، تتم مطابقة كل\(x\) قيمة -value بقيمة\(y\) -value واحدة فقط.
استخدمنا مثال عيد الميلاد لمساعدتنا على فهم التعريف. كل شخص لديه عيد ميلاد، ولكن لا أحد لديه عيد ميلاد، ولا بأس أن يشارك شخصان عيد ميلاد. نظرًا لأن كل شخص لديه عيد ميلاد واحد بالضبط، فإن هذه العلاقة هي وظيفة.

تكون الدالة واحدة لواحد إذا كانت كل قيمة في النطاق تحتوي على عنصر واحد بالضبط في المجال. بالنسبة لكل زوج مرتب في الدالة، تتم مطابقة كل قيمة y بقيمة -value واحدة\(x\) فقط.
مثالنا لعلاقة عيد الميلاد ليس وظيفة فردية. يمكن لشخصين مشاركة نفس تاريخ الميلاد. قيمة النطاق 2 أغسطس هي تاريخ ميلاد Liz و June، وبالتالي فإن قيمة النطاق الواحدة لها قيمتان للنطاق. لذلك، لا تكون الوظيفة واحدة إلى واحدة.
تكون الدالة واحدة إلى واحدة إذا كانت كل قيمة في النطاق تتوافق مع عنصر واحد في المجال. لكل زوج مرتب في الدالة، تتم مطابقة كل\(y\) قيمة -value بقيمة\(x\) -value واحدة فقط. لا توجد\(y\) قيم -متكررة.
بالنسبة لكل مجموعة من الأزواج المرتبة، حدد ما إذا كانت تمثل دالة، وإذا كان الأمر كذلك، ما إذا كانت الدالة واحدة إلى واحدة.
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
الحل:
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
تتم مطابقة كل\(x\) قيمة -value بقيمة\(y\) -value واحدة فقط. لذلك هذه العلاقة هي وظيفة.
لكن كل\(y\) قيمة -value لا يتم إقرانها\(x\) بقيمة -value واحدة فقط\((3,27)\)،\((−3,27)\) وعلى سبيل المثال. لذا فإن هذه الوظيفة ليست واحدة إلى واحدة.
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
تتم مطابقة كل\(x\) قيمة -value بقيمة\(y\) -value واحدة فقط. لذلك هذه العلاقة هي وظيفة.
نظرًا لأن كل\(y\) قيمة -يتم إقرانها بقيمة\(x\) -value واحدة فقط، فإن هذه الوظيفة تكون واحدًا لواحد.
بالنسبة لكل مجموعة من الأزواج المرتبة، حدد ما إذا كانت تمثل دالة أم لا، وإذا كان الأمر كذلك، فهي الدالة واحدة إلى واحدة.
- \(\{(-3,-6),(-2,-4),(-1,-2),(0,0),(1,2),(2,4),(3,6)\}\)
- \(\{(-4,8),(-2,4),(-1,2),(0,0),(1,2),(2,4),(4,8)\}\)
- إجابة
-
- وظيفة واحدة إلى واحدة
- الوظيفة؛ ليست واحدة لواحد
بالنسبة لكل مجموعة من الأزواج المرتبة، حدد ما إذا كانت تمثل دالة أم لا، وإذا كان الأمر كذلك، فهي الدالة واحدة إلى واحدة.
- \(\{(27,-3),(8,-2),(1,-1),(0,0),(1,1),(8,2),(27,3)\}\)
- \(\{(7,-3),(-5,-4),(8,0),(0,0),(-6,4),(-2,2),(-1,3)\}\)
- إجابة
-
- ليست وظيفة
- الوظيفة؛ ليست واحدة لواحد
لمساعدتنا في تحديد ما إذا كانت العلاقة دالة أم لا، نستخدم اختبار الخط العمودي. مجموعة النقاط في نظام الإحداثيات المستطيل هي الرسم البياني للدالة إذا كان كل خط عمودي يتقاطع مع الرسم البياني في نقطة واحدة على الأكثر. أيضًا، إذا تقاطع أي خط عمودي مع الرسم البياني في أكثر من نقطة، فإن الرسم البياني لا يمثل دالة.
يمثل الخط العمودي\(x\) قيمة -value ونتحقق من أنه يتقاطع مع الرسم البياني في\(y\) قيمة -واحدة فقط. ثم إنها وظيفة.
للتحقق مما إذا كانت الوظيفة واحدة لواحد، نستخدم عملية مماثلة. نستخدم خطًا أفقيًا ونتحقق من أن كل خط أفقي يتقاطع مع الرسم البياني في نقطة واحدة فقط. يمثل الخط الأفقي\(y\) قيمة -value ونتحقق من أنه يتقاطع مع الرسم البياني في\(x\) قيمة -واحدة فقط. إذا كان كل خط أفقي يتقاطع مع الرسم البياني لدالة في نقطة واحدة على الأكثر، فهي دالة واحدة إلى واحدة. هذا هو اختبار الخط الأفقي.
اختبار الخط الأفقي
إذا كان كل خط أفقي يتقاطع مع الرسم البياني لدالة في نقطة واحدة على الأكثر، فهي دالة واحدة إلى واحدة.
يمكننا اختبار ما إذا كان الرسم البياني للعلاقة دالة باستخدام اختبار الخط العمودي. يمكننا بعد ذلك معرفة ما إذا كانت الوظيفة واحدة لواحد من خلال تطبيق اختبار الخط الأفقي.
تحديد
- ما إذا كان كل رسم بياني يمثل رسمًا بيانيًا لدالة، وإذا كان الأمر كذلك،
- سواء كان من شخص إلى واحد
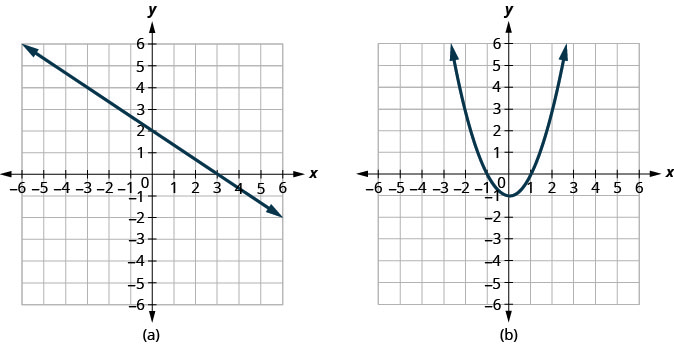
الحل:
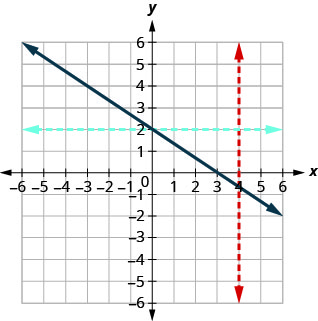
الشكل 10.1.40
نظرًا لأن أي خط عمودي يتقاطع مع الرسم البياني في نقطة واحدة على الأكثر، فإن الرسم البياني هو الرسم البياني للدالة. نظرًا لأن أي خط أفقي يتقاطع مع الرسم البياني في نقطة واحدة على الأكثر، فإن الرسم البياني هو الرسم البياني لدالة فردية.
ب.
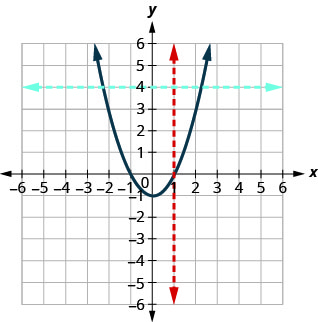
نظرًا لأن أي خط عمودي يتقاطع مع الرسم البياني في نقطة واحدة على الأكثر، فإن الرسم البياني هو الرسم البياني للدالة. الخط الأفقي الموضح على الرسم البياني يتقاطعه في نقطتين. لا يمثل هذا الرسم البياني دالة فردية.
تحديد
- ما إذا كان كل رسم بياني يمثل رسمًا بيانيًا لدالة، وإذا كان الأمر كذلك،
- سواء كان من شخص إلى واحد
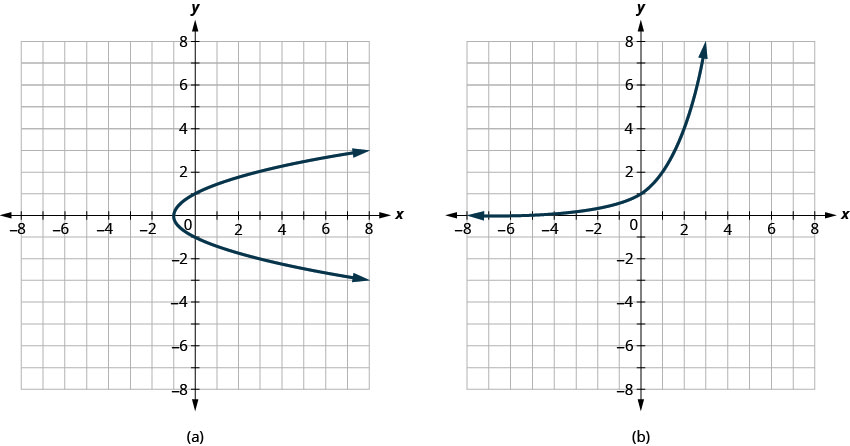
- إجابة
-
- ليست وظيفة
- وظيفة واحدة إلى واحدة
تحديد
- ما إذا كان كل رسم بياني يمثل رسمًا بيانيًا لدالة، وإذا كان الأمر كذلك،
- سواء كان من شخص إلى واحد
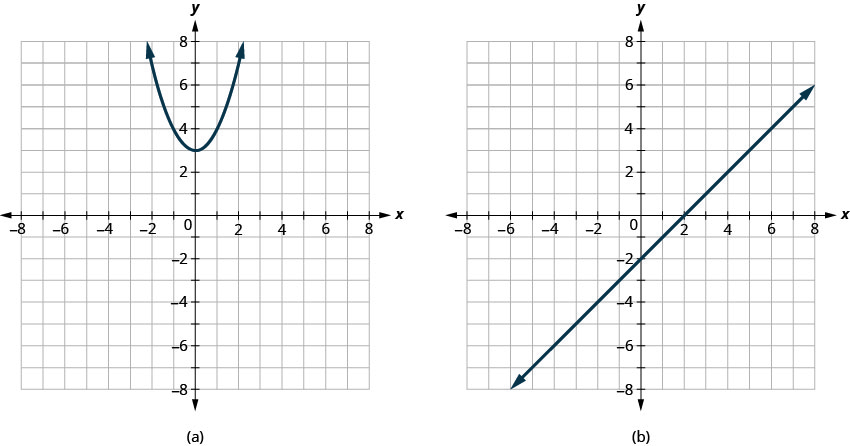
- إجابة
-
- الوظيفة؛ ليست واحدة لواحد
- وظيفة واحدة إلى واحدة
أوجد معكوس الدالة
لنلقِ نظرة على دالة واحدة إلى واحدة\(f\)، ممثلة بالأزواج المرتبة\(\{(0,5),(1,6),(2,7),(3,8)\}\). لكل\(x\) قيمة -value،\(f\) أضف\(5\) للحصول على\(y\) القيمة -value. من أجل «التراجع» عن الإضافة\(5\)، نطرح\(5\) من كل\(y\) قيمة -value ونعود إلى\(x\) القيمة -الأصلية. يمكننا تسمية هذا بـ «أخذ معكوس\(f\)» وتسمية الدالة\(f^{−1}\).
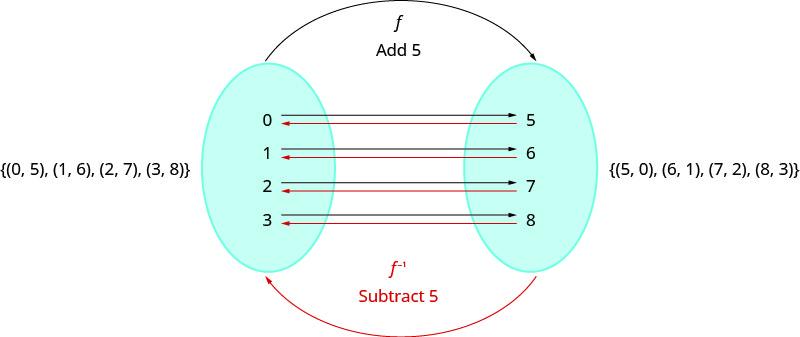
لاحظ أن الأزواج المرتبة من\(f\)\(x\) قيم\(y\) -والقيم الخاصة بها معكوسة.\(f^{−1}\) المجال\(f\) هو النطاق\(f^{−1}\) والمجال\(f^{−1}\) هو نطاق\(f\).
معكوس الدالة المُعرَّفة بالأزواج المرتبة
\(f(x)\)إذا كانت دالة من دالة واحدة إلى واحدة تكون أزواجها المرتبة من الشكل\((x,y)\)، فإن الدالة العكسية\(f^{−1}(x)\) هي مجموعة الأزواج المرتبة\((y,x)\).
في المثال التالي سنجد معكوس الدالة المحددة بالأزواج المرتبة.
أوجد معكوس الدالة\(\{(0,3),(1,5),(2,7),(3,9)\}\). حدِّد مجال ومدى الدالة العكسية.
الحل:
هذه الوظيفة فردية نظرًا لأن كل\(x\) قيمة -يتم إقرانها بقيمة\(y\) -value واحدة بالضبط.
للعثور على المعكوس، نقوم بعكس\(x\) قيم\(y\) -والقيم -في الأزواج المرتبة للدالة.
\(\begin{array}{ll} {\text{Function}}&{\{(0,3),(1,5),(2,7),(3,9)\}} \\ {\text{Inverse Function}}& {\{(3,0), (5,1), (7,2), (9,3)\}} \\ {\text{Domain of Inverse Function}}&{\{3, 5, 7, 9\}} \\ {\text{Range of Inverse Function}}&{\{0, 1, 2, 3\}} \end{array}\)
أوجد معكوس\(\{(0,4),(1,7),(2,10),(3,13)\}\). حدِّد مجال ومدى الدالة العكسية.
- إجابة
-
دالة عكسية:\(\{(4,0),(7,1),(10,2),(13,3)\}\). اسم النطاق:\(\{4,7,10,13\}\). النطاق:\(\{0,1,2,3\}\).
أوجد معكوس\(\{(-1,4),(-2,1),(-3,0),(-4,2)\}\). حدِّد مجال ومدى الدالة العكسية.
- إجابة
-
دالة عكسية:\(\{(4,-1),(1,-2),(0,-3),(2,-4)\}\). اسم النطاق:\(\{0,1,2,4\}\). النطاق:\(\{-4,-3,-2,-1\}\).
لقد لاحظنا للتو\(f(x)\) أنه إذا كانت دالة فردية تكون أزواجها المرتبة من الشكل\((x,y)\)، فإن الدالة العكسية\(f^{−1}(x)\) هي مجموعة الأزواج المرتبة\((y,x)\).
لذلك إذا كانت\((a,b)\) النقطة على الرسم البياني للدالة\(f(x)\)، فسيكون الزوج\((b,a)\) المُرتب على الرسم البياني لـ\(f^{−1}(x)\). انظر الشكل 10.1.43.
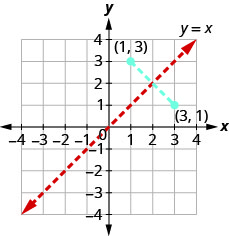
المسافة بين أي زوجين\((a,b)\)\((b,a)\) ويتم قطعها إلى النصف بواسطة الخط\(y=x\). لذلك نقول أن النقاط هي صور معكوسة لبعضها البعض عبر الخط\(y=x\).
نظرًا لأن كل نقطة على الرسم البياني\(f(x)\) للدالة هي صورة معكوسة لنقطة على الرسم البياني\(f^{−1}(x)\)، فإننا نقول إن الرسوم البيانية هي صور معكوسة لبعضها البعض عبر الخط\(y=x\). سنستخدم هذا المفهوم لرسم معكوس الدالة في المثال التالي.
رسم بياني، على نفس النظام الإحداثي، يظهر معكوس الدالة من واحد إلى واحد.
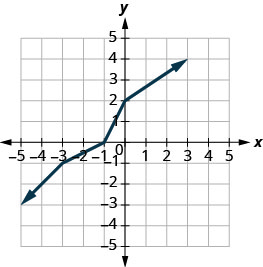
الحل:
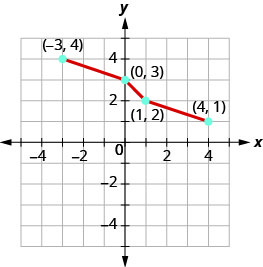
يمكننا استخدام النقاط على الرسم البياني للعثور على نقاط على الرسم البياني العكسي. بعض النقاط على الرسم البياني هي:\((−5,−3),(−3,−1),(−1,0),(0,2),(3,4)\).
لذلك، ستحتوي الدالة العكسية على النقاط:\((−3,−5),(−1,−3),(0,−1),(2,0),(4,3)\).
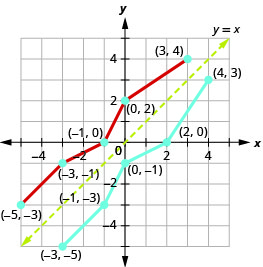
لاحظ كيف أن الرسم البياني للدالة الأصلية والرسم البياني للدوال العكسية عبارة عن صور معكوسة عبر الخط\(y=x\).
رسم بياني، على نفس نظام الإحداثيات، معكوس الدالة من واحد إلى واحد.
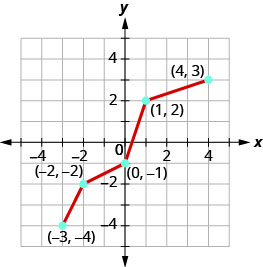
- إجابة
-
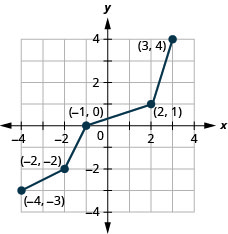
الشكل 10.1.49
رسم بياني، على نفس نظام الإحداثيات، معكوس الدالة من واحد إلى واحد.
- إجابة
-
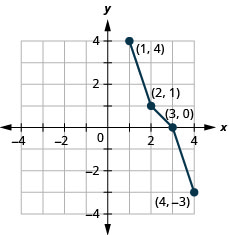
الشكل 10.1.51
عندما بدأنا مناقشتنا للدالة العكسية، تحدثنا عن كيفية قيام الدالة العكسية «بالتراجع» عما فعلته الدالة الأصلية بقيمة في مجالها من أجل العودة إلى\(x\) القيمة -الأصلية.

الدوال العكسية
\(f^{-1}(f(x))=x\)، للجميع\(x\) في مجال\(f\)
\(f\left(f^{-1}(x)\right)=x\)، للجميع\(x\) في مجال\(f^{-1}\)
يمكننا استخدام هذه الخاصية للتحقق من أن وظيفتين معكوستين لبعضهما البعض.
تحقق من ذلك\(f(x)=5x−1\)\(g(x)=\frac{x+1}{5}\) وهي وظائف عكسية.
الحل:
تعتبر الوظائف معكوسات عن بعضها البعض إذا كان الأمر\(g(f(x))=x\) كذلك\(f(g(x))=x\).
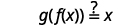 |
|
| بديل\(5x-1\) لـ\(f(x)\). | 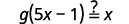 |
 |
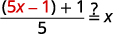 |
| قم بالتبسيط. | 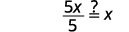 |
| قم بالتبسيط. | 
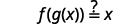
|
| بديل\(\frac{x+1}{5}\) عن\(g(x)\). | 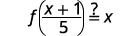 |
 |
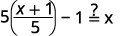 |
| قم بالتبسيط. | 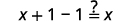 |
| قم بالتبسيط. |  |
وبما أن كليهما\(g(f(x))=x\)\(f(g(x))=x\) صحيحان، فإن\(f(x)=5x−1\) الدوال\(g(x)=\frac{x+1}{5}\) هي وظائف عكسية. أي أنها معكوسات عن بعضها البعض.
تحقق من أن الوظائف هي وظائف عكسية. \(f(x)=4 x-3\)و\(g(x)=\frac{x+3}{4}\).
- إجابة
-
\(g(f(x))=x\)\(f(g(x))=x\)، وبالتالي فهي معكوسة.
تحقق من أن الوظائف هي وظائف عكسية. \(f(x)=2 x+6\)و\(g(x)=\frac{x-6}{2}\)
- إجابة
-
\(g(f(x))=x,\)\(f(g(x))=x,\)وبالتالي فهي معكوسة.
لقد وجدنا معكوسات الدالة المحددة بالأزواج المرتبة ومن الرسم البياني. سننظر الآن في كيفية إيجاد معكوس باستخدام معادلة جبرية. تستخدم الطريقة فكرة\(f(x)\) أنه إذا كانت دالة فردية ذات أزواج مرتبة\((x,y)\)، فإن الدالة العكسية\(f^{−1}(x)\) هي مجموعة الأزواج المرتبة\((y,x)\).
إذا عكسنا\(x\) النقطة and\(y\) في الدالة ثم حلنا لها\(y\)، نحصل على الدالة العكسية.
أوجد معكوس\(f(x)=4 x+7\).
الحل:
| الخطوة 1. بديل\(y\) عن\(f(x)\). | استبدل\(f(x)\) بـ\(y\). | \(\begin{aligned} f(x) &=4 x+7 \\ y &=4 x+7 \end{aligned}\) |
| الخطوة 2: تبادل المتغيرات\(x\) و\(y\). | استبدل\(x\) بـ\(y\) ثم\(y\) بـ\(x\). | \(x=4y+7\) |
| الخطوة 3: حل لـ\(y\). |
اطرح\(7\) من كل جانب. اقسم على\(4\). |
\(x-7=4 y\) \(\frac{x-7}{4}=y\) |
| الخطوة 4: بديل\(f^{-1}(x)\) عن\(y\). | استبدل\(y\) بـ\(f^{-1}(x)\). | \(\frac{x-7}{4}=f^{-1}(x)\) |
| الخطوة 5: تحقق من أن الوظائف معكوسة. |
عرض\(f^{-1}(f(x))=x\) و\(f\left(f^{-1}(x)\right)=x\) |
\(\begin{aligned} f^{-1}(f(x)) & \stackrel{?}{=} x \\f^{-1}(4x+7)&\stackrel{?}{=}x\\ \frac{(4x+7)-7}{4}&\stackrel{?}{=}x \\ \frac{4x}{4}&\stackrel{?}{=}x\\x&=x \\ \\f(f^{-1}(x))&\stackrel{?}{=}x \\f \left(\frac{x-7}{4} \right)&\stackrel{?}{=}x \\ 4\left(\frac{x-7}{4} \right) + 7 &\stackrel{?}{=}x \\ x-7+7&\stackrel{?}{=}x \\x&=x \end{aligned}\) |
أوجد معكوس الدالة\(f(x)=5x-3\).
- إجابة
-
\(f^{-1}(x)=\frac{x+3}{5}\)
أوجد معكوس الدالة\(f(x)=8 x+5\).
- إجابة
-
\(f^{-1}(x)=\frac{x-5}{8}\)
نحن نلخص الخطوات أدناه.
كيفية إيجاد معكوس دالة من واحد إلى واحد
- بديل\(y\) عن\(f(x)\).
- قم بتبادل المتغيرات\(x\) و\(y\).
- حل لـ\(y\).
- بديل\(f^{−1}(x)\) عن\(y\).
- تحقق من أن الوظائف معكوسة.
أوجد معكوس\(f(x)=\sqrt[5]{2 x-3}\).
الحل:
\(f(x)=\sqrt[5]{2 x-3}\)
بديل\(y\) عن\(f(x)\).
\(y=\sqrt[5]{2 x-3}\)
قم بتبادل المتغيرات\(x\) و\(y\).
\(x=\sqrt[5]{2 y-3}\)
حل لـ\(y\).
\(\begin{aligned}(x)^{5} &=(\sqrt[5]{2 y-3})^{5} \\ x^{5} &=2 y-3 \\ x^{5}+3 &=2 y \\ \frac{x^{5}+3}{2} &=y \end{aligned}\)
بديل\(f^{-1}(x)\) عن\(y\).
\(f^{-1}(x)=\frac{x^{5}+3}{2}\)
تحقق من أن الوظائف معكوسة.
\(\begin{array}{rr} {f^{-1}(f(x)) \stackrel{?}{=} x} & {f\left(f^{-1}(x)\right) \stackrel{?}{=} x} \\ {f^{-1}(\sqrt[5]{2x-3})\stackrel{?}{=}x}&{f\left(\frac{x^{5}+3}{2} \right)}\stackrel{?}{=}x \\ {\frac{(\sqrt[5]{2x-3})^{5}+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{2\left(\frac{x^{5}+3}{2} \right)-3}\stackrel{?}{=}x} \\ {\frac{2x-3+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}+3-3}\stackrel{?}{=}x}\\ {\frac{2x}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}}\stackrel{?}{=}x} \\ {x=x}&{x=x} \end{array}\)
أوجد معكوس الدالة\(f(x)=\sqrt[5]{3 x-2}\).
- إجابة
-
\(f^{-1}(x)=\frac{x^{5}+2}{3}\)
أوجد معكوس الدالة\(f(x)=\sqrt[4]{6 x-7}\).
- إجابة
-
\(f^{-1}(x)=\frac{x^{4}+7}{6}\)
المفاهيم الرئيسية
- تكوين الوظائف: تكوين الوظائف\(g\)،\(f\) ويتم كتابته\(f∘g\) وتعريفه بواسطة
\((f \circ g)(x)=f(g(x))\)
نقرأ\(f(g(x))\) اعتبارًا\(f\)\(g\) من\(x\). - اختبار الخط الأفقي: إذا كان كل خط أفقي يتقاطع مع الرسم البياني لدالة في نقطة واحدة على الأكثر، فهي دالة فردية.
- معكوس الدالة المُعرَّفة بالأزواج المرتبة:\(f(x)\) إذا كانت دالة من دالة واحدة إلى واحدة تكون أزواجها المرتبة من الشكل\((x,y)\)، فإن الدالة العكسية لها\(f^{−1}(x)\) هي مجموعة الأزواج المرتبة\((y,x)\).
- الدوال العكسية: لكل وظيفة\(x\) في مجال دالة واحدة إلى واحدة\(f\) و\(f^{−1}\)،
\(f^{-1}(f(x))=x\)
\(f\left(f^{-1}(x)\right)=x\) - كيفية العثور على معكوس دالة واحدة إلى واحدة:
- بديل\(y\) عن\(f(x)\).
- قم بتبادل المتغيرات\(x\) و\(y\).
- حل لـ\(y\).
- بديل\(f^{−1}(x)\) عن\(y\).
- تحقق من أن الوظائف معكوسة.
مسرد المصطلحات
- وظيفة واحد لواحد
- تكون الدالة واحدة لواحد إذا كانت كل قيمة في النطاق تحتوي على عنصر واحد بالضبط في المجال. لكل زوج مرتب في الدالة، تتم مطابقة كل\(y\) قيمة -value بقيمة\(x\) -value واحدة فقط.


