7.7: حل المتباينات العقلانية

Last updated
Save as PDF

Page ID: 201743

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

حل عدم المساواة العقلانية
حل عدم المساواة باستخدام الوظائف العقلانية

كن مستعدًا

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

ابحث عن قيمة$x-5$ متى ⓐ$x=6$ ⓑ$x=-3$ ⓒ$x=5$
إذا فاتتك هذه المشكلة، راجع المثال 1.2.16.
الحل:$8-2 x<12$
إذا فاتتك هذه المشكلة، راجع المثال 2.6.13.
اكتب بالتدوين الفاصل الزمني:$-3 \leq x<5 $
إذا فاتتك هذه المشكلة، راجع المثال 2.6.4.

حل المتباينات العقلانية

تعلمنا حل المتباينات الخطية بعد تعلم حل المعادلات الخطية. كانت التقنيات متشابهة إلى حد كبير مع استثناء رئيسي واحد. عندما نضرب أو نقسم على رقم سالب، تنعكس علامة عدم المساواة.

بعد أن تعلمنا للتو حل المعادلات العقلانية، نحن الآن على استعداد لحل عدم المساواة العقلانية. عدم المساواة العقلانية هي عدم المساواة التي تحتوي على تعبير عقلاني.

عدم المساواة العقلانية

عدم المساواة العقلانية هي عدم المساواة التي تحتوي على تعبير عقلاني.

عدم المساواة مثل$\quad \dfrac{3}{2 x}>1, \quad \dfrac{2 x}{x-3}<4, \quad \dfrac{2 x-3}{x-6} \geq x,\quad$ وعدم المساواة العقلانية$\quad \dfrac{1}{4}-\dfrac{2}{x^{2}} \leq \dfrac{3}{x}\quad $ لأن كل منها يحتوي على تعبير عقلاني.

عندما نحل عدم المساواة العقلانية، سنستخدم العديد من التقنيات التي استخدمناها لحل عدم المساواة الخطية. يجب أن نتذكر بشكل خاص أنه عندما نضرب أو نقسم برقم سالب، يجب عكس علامة عدم المساواة.

الفرق الآخر هو أنه يجب علينا التفكير بعناية في القيمة التي قد تجعل التعبير العقلاني غير محدد وبالتالي يجب استبعاده.

عندما نحل معادلة والنتيجة هي$x=3$، نعلم أن هناك حلًا واحدًا، وهو 3.

عندما نحل مشكلة عدم المساواة والنتيجة هي$x>3$ أننا نعلم أن هناك العديد من الحلول. نحن نرسم النتيجة للمساعدة بشكل أفضل في عرض جميع الحلول، ونبدأ بـ 3. تصبح النقطة الثالثة نقطة حرجة ثم نقرر ما إذا كنا سنظل على يسارها أو يمينها. الأرقام الموجودة على يمين 3 أكبر من 3، لذلك نظل إلى اليمين.

$clipboard_e564fdf3437198939cd8bf44061cfa74e.png$

لحل مشكلة عدم المساواة المنطقية، يجب علينا أولاً كتابة عدم المساواة باستخدام حاصل واحد فقط على اليسار و0 على اليمين.

بعد ذلك نحدد النقاط الحرجة التي يجب استخدامها لتقسيم خط الأرقام إلى فترات. النقطة الحرجة هي الرقم الذي يجعل التعبير العقلاني صفرًا أو غير محدد.

سنقوم بعد ذلك بتقييم عوامل البسط والمقام، وإيجاد حاصل القسمة في كل فترة. سيحدد هذا الفاصل الزمني أو الفواصل الزمنية التي تحتوي على جميع حلول عدم المساواة العقلانية.

نكتب الحل بالتدوين الفاصل الزمني مع الحرص على تحديد ما إذا كانت نقاط النهاية مضمنة أم لا.

مثال$\PageIndex{1}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{x-1}{x+3} \geq 0$

الحل

الخطوة 1. اكتب عدم المساواة في صورة حاصل قسمة واحد على اليسار وصفر على اليمين.

عدم المساواة لدينا في هذا الشكل. \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]

الخطوة 2. حدد النقاط الحرجة - النقاط التي سيكون فيها التعبير العقلاني صفرًا أو غير محدد.

سيكون التعبير العقلاني صفرًا عندما يكون البسط صفرًا. منذ$x-1=0$ متى$x=1$، أصبحت 1 نقطة حرجة.

لن يتم تعريف التعبير العقلاني عندما يكون المقام صفرًا. منذ$x+3=0$ متى$x=-3$، تعد -3 نقطة حرجة.

النقاط الحرجة هي 1 و -3.

الخطوة 3. استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فواصل زمنية.

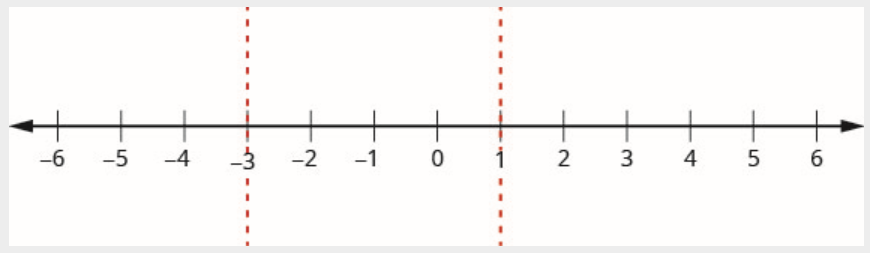
$clipboard_e431a0043d1c5bb7e4b4d0de15dc59cbc.png$

يتم تقسيم خط الأرقام إلى ثلاث فترات:

\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonumber \]

الخطوة 4. اختبر قيمة في كل فاصل زمني. تظهر فوق خط الأعداد علامة كل عامل من عوامل التعبير العقلاني في كل فاصل زمني. أسفل خط الأرقام تظهر علامة حاصل القسمة.

للعثور على علامة كل عامل في الفاصل الزمني، نختار أي نقطة في تلك الفترة ونستخدمها كنقطة اختبار. أي نقطة في الفاصل الزمني ستعطي التعبير نفس العلامة، حتى نتمكن من اختيار أي نقطة في الفاصل الزمني.

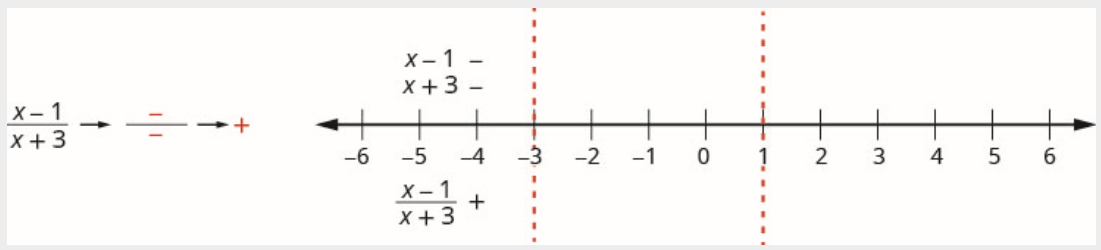
\[\text { Interval }(-\infty,-3) \nonumber \]

الرقم -4 في الفاصل الزمني$(-\infty,-3)$. اختبر التعبير$x=-4$ في البسط والمقام.

البسط:

\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Negative}} \end{array} \nonumber \]

القاسم:

\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]

فوق خط الأعداد، حدد العامل$x-1$ السالب وحدد العامل$x+3$ السالب.

نظرًا لأن السالب مقسومًا على سالب يكون موجبًا، ضع علامة على حاصل القسمة الموجب في الفاصل الزمني$(-\infty,-3)$

$clipboard_e4d5ff31fd44e4c2b9e0115f2b58099f8.png$

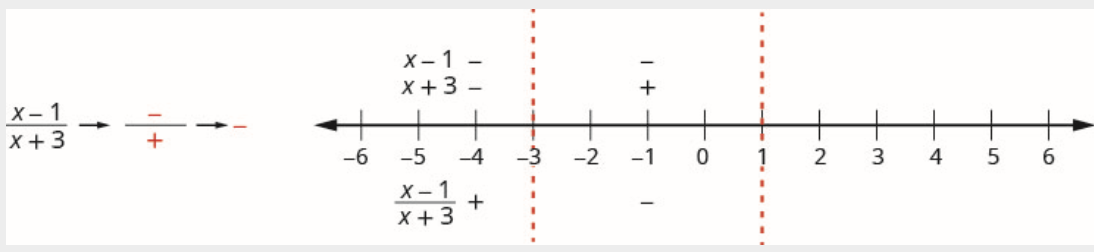
\[\text {Interval } (-3,1) \nonumber \]

الرقم 0 موجود في الفاصل الزمني$(-3,1)$. اختبار$x=0$.

البسط:

\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]

القاسم:

\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Positive}} \end{array} \nonumber \]

فوق خط الأعداد، حدد العامل$x-1$ السالب وحدد$x+3$ الموجب.

نظرًا لأن السالب مقسومًا على موجب يكون سالبًا، يتم وضع علامة سالب على حاصل القسمة في الفاصل الزمني$(-3,1)$.

$clipboard_ee9a065f5ae1eb4312d2506f46f91b4f5.png$

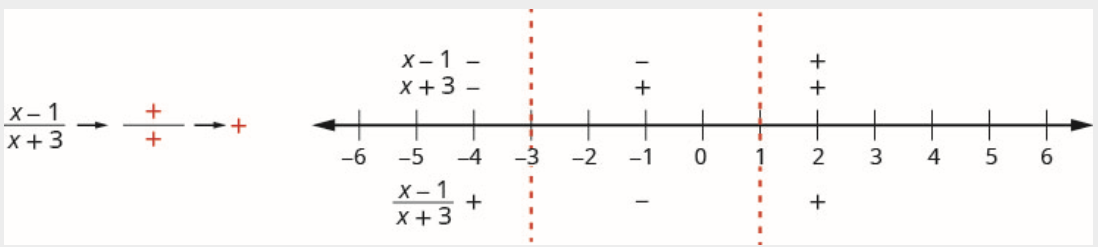
\[\text {Interval }(1, \infty) \nonumber \]

الرقم 2 موجود في الفاصل الزمني$(1, \infty)$. اختبار$x=2$.

البسط:

\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]

القاسم:

\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Positive}} \end{array} \nonumber \]

فوق خط الأعداد، حدد العامل$x-1$ الموجب وقم بوضع علامة$x+3$ إيجابية.

بما أن الموجب المقسوم على الموجب إيجابي، ضع علامة على حاصل القسمة الموجب في الفاصل الزمني$(1, \infty)$.

$clipboard_e9f05dbda07764ab489a7211f1b930f81.png$

الخطوة 5. حدد الفترات التي يكون فيها عدم المساواة صحيحًا. اكتب الحل بالتدوين الفاصل الزمني.

نريد أن يكون حاصل القسمة أكبر من أو يساوي الصفر، وبالتالي فإن الأرقام في الفواصل الزمنية$(-\infty,-3)$$(1, \infty) $ هي حلول.

ولكن ماذا عن النقاط الحرجة؟

النقطة الحرجة$x=-3$ تجعل المقام 0، لذلك يجب استبعاده من الحل ونقوم بتمييزه بقوس.

النقطة الحرجة$x=1$ تجعل التعبير العقلاني بأكمله 0. يتطلب عدم المساواة أن يكون التعبير العقلاني أكبر من أو مساويًا لـ. لذلك، 1 هو جزء من الحل وسنقوم بتمييزه بقوس.

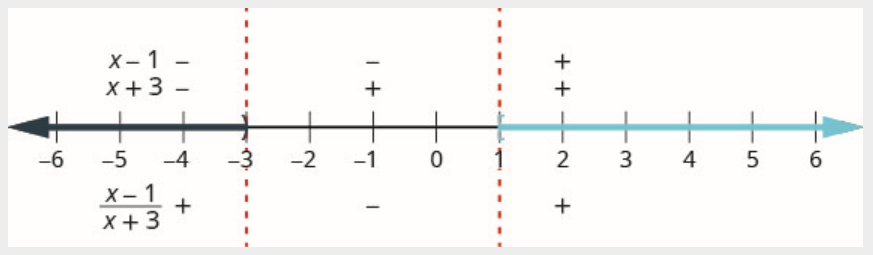
$clipboard_eff4e23ab54188da0d5229b26f9790bb8.png$

تذكر أنه عندما يكون لدينا حل يتكون من أكثر من فاصل زمني، فإننا نستخدم رمز الاتحاد$\cup $، لربط الفواصل الزمنية. الحل في الترميز الفاصل هو$(-\infty,-3) \cup[1, \infty)$.

التمارين$\PageIndex{1}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{x-2}{x+4} \geq 0$

إجابة: $(-\infty,-4) \cup[2, \infty)$

التمارين$\PageIndex{2}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{x+2}{x-4} \geq 0$

إجابة: $(-\infty,-2] \cup(4, \infty)$

نحن نلخص الخطوات للرجوع إليها بسهولة.

كيفية حل عدم المساواة العقلانية

الخطوة 1. اكتب عدم المساواة في صورة حاصل قسمة واحد على اليسار وصفر على اليمين.

الخطوة 2. حدد النقاط الحرجة - النقاط التي سيكون فيها التعبير العقلاني صفرًا أو غير محدد.

الخطوة 3. استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فواصل زمنية.

الخطوة 4. اختبر قيمة في كل فاصل زمني. تظهر فوق خط الأعداد علامة كل عامل من عوامل البسط والمقام في كل فاصل زمني. أسفل خط الأرقام تظهر علامة حاصل القسمة.

الخطوة 5. حدد الفترات التي يكون فيها عدم المساواة صحيحًا. اكتب الحل بالتدوين الفاصل الزمني.

يتطلب المثال التالي أن نحصل أولاً على عدم المساواة العقلانية في الشكل الصحيح.

مثال$\PageIndex{2}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{4 x}{x-6}<1$

الحل

\[\dfrac{4 x}{x-6}<1 \nonumber \]

اطرح 1 للحصول على صفر على اليمين.

\[\dfrac{4 x}{x-6}-1<0 \nonumber \]

أعد كتابة 1 ككسر باستخدام شاشة LCD.

\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]

اطرح البسط، ثم ضع الفرق على المقام المشترك.

\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]

قم بالتبسيط.

\[\dfrac{3 x+6}{x-6}<0 \nonumber \]

ضع البسط في الاعتبار لإظهار جميع العوامل.

\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]

ابحث عن النقاط الحرجة.

سيكون حاصل القسمة صفرًا عندما يكون البسط صفرًا. لا يتم تعريف حاصل القسمة عندما يكون المقام صفرًا.

\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & {=6} \end{array} \nonumber \]

استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فواصل زمنية.

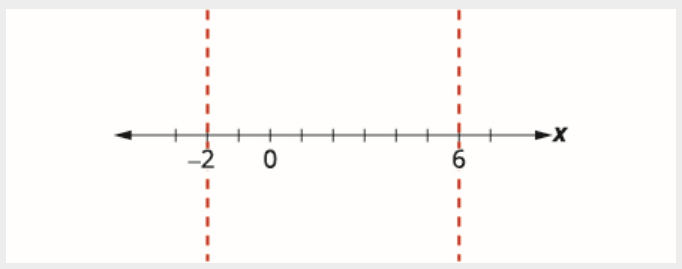
$clipboard_e21abd0b663d106757f6f6e723393df4e.png$

اختبر قيمة في كل فاصل زمني.

	\((-\infty,-2)\)	\((-2,6)\)	\((6, \infty)\)
\(x+2)\)	\ (-\ إنفتي، -2)\)» النمط = «محاذاة رأسية: متوسطة؛» class= «lt-matth-5164"> x+2 -3+2 -1 -	\ (-2,6)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164"> x+2 0+2 2 +	\ ((6,\ infty)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164"> x+2 7+2 9 +
\(x-6\)	\ (-\ إنفتي، -2)\)» النمط = «محاذاة رأسية: متوسطة؛» class= «lt-matth-5164"> إكس-6 -3-6 -9 -	\ (-2,6)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164"> إكس-6 0-6 -6 -	\ ((6,\ infty)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164"> إكس-6 7-6 1 +

$(-\infty,-2)$

$(-2,6)$

$(6, \infty)$

$x+2)$

\ (-\ إنفتي، -2)\)» النمط = «محاذاة رأسية: متوسطة؛» class= «lt-matth-5164">

x+2

-3+2

-1

\ (-2,6)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164">

x+2

0+2

\ ((6,\ infty)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164">

x+2

7+2

$x-6$

\ (-\ إنفتي، -2)\)» النمط = «محاذاة رأسية: متوسطة؛» class= «lt-matth-5164">

إكس-6

-3-6

-9

\ (-2,6)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164">

إكس-6

0-6

-6

\ ((6,\ infty)\)» النمط = «المحاذاة الرأسية: الوسطى؛» class= «lt-math-5164">

إكس-6

7-6

تظهر فوق خط الأعداد علامة كل عامل من عوامل التعبير العقلاني في كل فاصل زمني. أسفل خط الأرقام تظهر علامة حاصل القسمة.

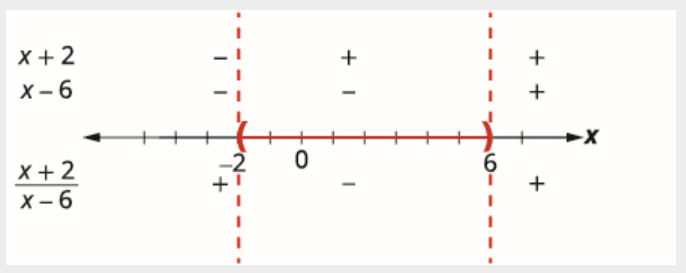
$clipboard_e667e7f41140a947d1fadb213a3b6434f.png$

حدد الفترات التي يكون فيها عدم المساواة صحيحًا. نريد أن يكون حاصل القسمة سالبًا، لذلك يتضمن الحل النقاط بين −2 و6. نظرًا لأن عدم المساواة أقل تمامًا من، لا يتم تضمين نقاط النهاية.

نكتب الحل بالتدوين الفاصل الزمني على النحو (−2، 6).

التمارين$\PageIndex{3}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{3 x}{x-3}<1$.

إجابة: $\left(-\dfrac{3}{2}, 3\right)$

التمارين$\PageIndex{4}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{3 x}{x-4}<2$.

إجابة: $(-8,4)$

في المثال التالي، يكون البسط دائمًا موجبًا، لذلك تعتمد علامة التعبير العقلاني على علامة المقام.

مثال$\PageIndex{3}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{5}{x^{2}-2 x-15}>0$.

الحل

عدم المساواة في الشكل الصحيح.

\[\dfrac{5}{x^{2}-2 x-15}>0 \nonumber \]

عامل المقام.

\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]

ابحث عن النقاط الحرجة. حاصل القسمة هو 0 عندما يكون البسط هو 0. نظرًا لأن البسط دائمًا هو 5، لا يمكن أن يكون حاصل القسمة 0.

لن يتم تعريف حاصل القسمة عندما يكون المقام صفرًا.

\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]

استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فواصل زمنية.

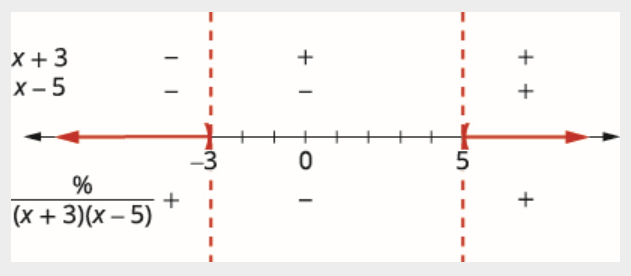
$clipboard_e021f22ee9a3dcabc95f9915aaa56196b.png$

قيم الاختبار في كل فاصل زمني. فوق خط الأعداد تظهر علامة كل عامل من عوامل المقام في كل فاصل زمني. أسفل خط الأعداد، اعرض علامة حاصل القسمة.

اكتب الحل بالتدوين الفاصل الزمني.

\[(-\infty,-3) \cup(5, \infty) \nonumber \]

Exercise $\PageIndex{5}$

Solve and write the solution in interval notation: $\dfrac{1}{x^{2}+2 x-8}>0$.

Answer: $(-\infty,-4) \cup(2, \infty)$

Exercise $\PageIndex{6}$

Solve and write the solution in interval notation: $\dfrac{3}{x^{2}+x-12}>0 $.

Answer: $(-\infty,-4) \cup(3, \infty)$

The next example requires some work to get it into the needed form.

Example $\PageIndex{4}$

Solve and write the solution in interval notation: $\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x}$.

Solution

\[\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x} \nonumber \]

Subtract $\dfrac{5}{3 x}$ to get zero on the right.

\[\dfrac{1}{3}-\dfrac{2}{x^{2}}-\dfrac{5}{3 x}<0 \nonumber \]

Rewrite to get each fraction with the LCD

\[\dfrac{1 \cdot x^{2}}{3 \cdot x^{2}}-\dfrac{2 \cdot 3}{x^{2} \cdot 3}-\dfrac{5 \cdot x}{3 x-x}<0 \nonumber \]

Simplify.

\[\dfrac{x^{2}}{3 x^{2}}-\dfrac{6}{3 x^{2}}-\dfrac{5 x}{3 x^{2}}<0 \nonumber \]

Subtract the numerators and place the difference over the common denominator.

\[\dfrac{x^{2}-5 x-6}{3 x^{2}}<0 \nonumber \]

Factor the numerator.

\[\dfrac{(x-6)(x+1)}{3 x^{2}}<0 \nonumber \]

Find the critical points.

\[\begin{array}{rlrl} {3 x^{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{array} \nonumber \]

Use the critical points to divide the number line into intervals.

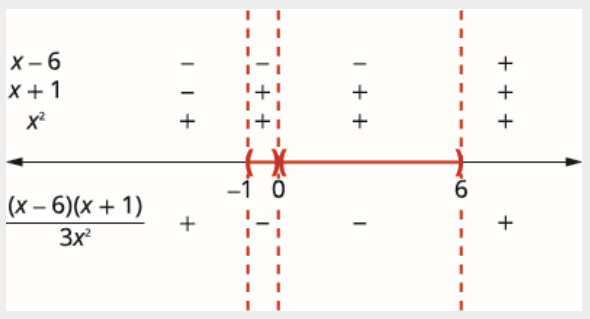
$clipboard_e782e665edacc8e08d9dc6bd0db2081e9.png$

فوق خط الأعداد تظهر علامة كل عامل في كل فاصل زمني. أسفل خط الأعداد، اعرض علامة حاصل القسمة.

نظرًا لاستبعاد 0، فإن الحل هو$(-1,0) \cup(0,6)$ الفواصل الزمنية،$(-1,0)$ و$(0,6)$.

التمارين$\PageIndex{7}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{1}{2}+\dfrac{4}{x^{2}}<\dfrac{3}{x}$.

إجابة: $(2,4)$

التمارين$\PageIndex{8}$

حل الحل واكتبه بتدوين الفاصل الزمني:$\dfrac{1}{3}+\dfrac{6}{x^{2}}<\dfrac{3}{x}$.

إجابة: $(3,6)$

حل عدم المساواة باستخدام الدوال الكسرية

عند التعامل مع الوظائف العقلانية، يكون من المفيد أحيانًا معرفة متى تكون الدالة أكبر من أو أقل من قيمة معينة. هذا يؤدي إلى عدم المساواة العقلانية.

مثال$\PageIndex{5}$

بمعلومية الدالة$R(x)=\dfrac{x+3}{x-5}$، ابحث عن قيم x التي تجعل الدالة أقل من أو تساوي 0.

الحل

نريد أن تكون الدالة أقل من أو تساوي 0.

\[R(x) \leq 0 \nonumber \]

استبدل التعبير العقلاني بـ$R(x)$.

\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]

ابحث عن النقاط الحرجة.

\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]

استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فواصل زمنية.

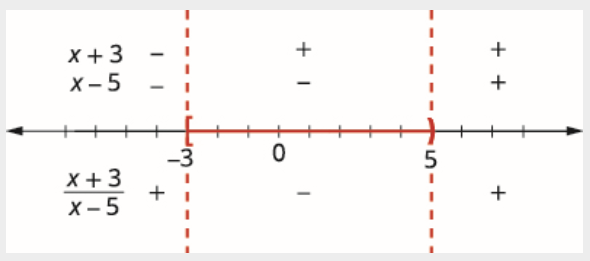
$clipboard_e76bb40ea8906c703f6c28ecf1b509d58.png$

قيم الاختبار في كل فاصل زمني. فوق خط الأعداد، اعرض علامة كل عامل في كل فاصل زمني. أسفل خط الأعداد، اعرض علامة حاصل القسمة. اكتب الحل بالتدوين الفاصل الزمني. نظرًا لاستبعاد 5، فإننا لا ندرجه في الفاصل الزمني.

\[[-3,5) \nonumber \]

Exercise $\PageIndex{9}$

Given the function $R(x)=\dfrac{x-2}{x+4}$, find the values of $x$ that make the function less than or equal to 0.

Answer: $(-4,2]$

Exercise $\PageIndex{10}$

Given the function $R(x)=\dfrac{x+1}{x-4}$, find the values of $x$ that make the function less than or equal to 0.

Answer: $[-1,4)$

In economics, the function $C(x)$ is used to represent the cost of producing $x$ units of a commodity. The average cost per unit can be found by dividing $C(x)$ by the number of items $x$. Then, the average cost per unit is \(c(x)=\dfrac{C(x)}{x}).

Example $\PageIndex{6}$

The function$C(x)=10 x+3000$ represents the cost to produce $x$, number of items. Find:

The average cost function, $c(x)$
How many items should be produced so that the average cost is less than $40.

Solution

\[C(x)=10 x+3000 \nonumber \]

The average cost function is $c(x)=\dfrac{C(x)}{x})$. To find the average cost function, divide the cost function by $x$.

\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]

The average cost function is $c(x)=\dfrac{10 x+3000}{x} $

We want the function $c(x)$ to be less than 40.

\[c(x)<40 \nonumber \]

Substitute the rational expression forc(x).

\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]

Subtract 40 to get 0 on the right.

\[\dfrac{10 x+3000}{x}-40<0 \nonumber \]

Rewrite the left side as one quotient by finding the LCD and performing the subtraction.

\[\begin{aligned} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &<0 \end{aligned} \nonumber \]

Factor the numerator to show all factors.

\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \end{array} \nonumber \]

Find the critical points.

\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]

More than 100 items must be produced to keep the average cost below $40 per item.

Exercise $\PageIndex{11}$

The function$C(x)=20 x+6000$ represents the cost to produce $x$, number of items. Find:

How many items should be produced so that the average cost is less than $60.

Answer

$c(x)=\dfrac{20 x+6000}{x}$
More than 150 items must be produced to keep the average cost below $60 per item.

Exercise $\PageIndex{12}$

The function$C(x)=5 x+900$ represents the cost to produce $x$, number of items. Find:

How many items should be produced so that the average cost is less than $20.

Answer

$c(x)=\dfrac{5 x+900}{x}$
More than 60 items must be produced to keep the average cost below $20 per item.

عدم المساواة العقلانية

مثال\(\PageIndex{1}\)

التمارين\(\PageIndex{1}\)

التمارين\(\PageIndex{2}\)

كيفية حل عدم المساواة العقلانية

مثال\(\PageIndex{2}\)

التمارين\(\PageIndex{3}\)

التمارين\(\PageIndex{4}\)

مثال\(\PageIndex{3}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Example \(\PageIndex{4}\)

التمارين\(\PageIndex{7}\)

التمارين\(\PageIndex{8}\)

مثال\(\PageIndex{5}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Example \(\PageIndex{6}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)