7.3: جمع وطرح التعبيرات الكسرية

ملخص

في نهاية هذا القسم، ستكون قادرًا على:

• جمع وطرح المقادير الكسرية ذات المقام المشترك
• جمع وطرح التعبيرات العقلانية التي تكون مقاماتها أضداد
• أوجد القاسم المشترك الأصغر للمقادير الكسرية
• جمع وطرح المقادير الكسرية ذات المقامات غير المتشابهة
• جمع وطرح الدوال الكسرية

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. إضافة:\(\dfrac{7}{10}+\dfrac{8}{15}\).
   إذا فاتتك هذه المشكلة، راجع [link].
2. طرح:\(\dfrac{3x}{4}−\dfrac{8}{9}\).
   إذا فاتتك هذه المشكلة، راجع [link].
3. طرح:\(6(2x+1)−4(x−5)\).
   إذا فاتتك هذه المشكلة، راجع [link].

جمع وطرح التعبيرات الكسرية ذات المقام المشترك

ما الخطوة الأولى التي تتخذها عند إضافة الكسور العددية؟ يمكنك التحقق مما إذا كان لديهم قاسم مشترك. إذا فعلوا ذلك، يمكنك إضافة البسط ووضع المجموع فوق المقام المشترك. إذا لم يكن لديهم قاسم مشترك، يمكنك العثور على واحد قبل الإضافة.

نفس الشيء مع التعبيرات العقلانية. لإضافة تعبيرات عقلانية، يجب أن يكون لها قاسم مشترك. عندما تكون المقامات متماثلة، يمكنك إضافة البسط ووضع المجموع فوق المقام المشترك.

الجمع والطرح للتعبير العقلاني

إذا كانت\(r\) كثيرة الحدود\(p\)\(q\)، وما زالت، أين\(r\neq 0\)، إذن

\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\]

لجمع أو طرح المقادير الكسرية ذات المقام المشترك، قم بجمع أو طرح البسط ووضع النتيجة فوق المقام المشترك.

نقوم دائمًا بتبسيط التعبيرات العقلانية. تأكد من مراعاة العوامل، إن أمكن، بعد طرح البسط حتى تتمكن من تحديد أي عوامل مشتركة.

تذكر أيضًا أننا لا نسمح بالقيم التي تجعل المقام صفرًا. ما القيمة التي\(x\) يجب استبعادها في المثال التالي؟

مثال\(\PageIndex{1}\)

إضافة:\(\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4}\).

الحل

بما أن المقام هو\(x+4\)، يجب علينا استبعاد القيمة\(x=−4\).

\(\begin{array} {ll} &\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4},\space x\neq −4 \\ \begin{array} {l} \text{The fractions have a common denominator,} \\ \text{so add the numerators and place the sum} \\ \text{over the common denominator.} \end{array} &\dfrac{11x+28+x^2}{x+4} \\ & \\ \text{Write the degrees in descending order.} &\dfrac{x^2+11x+28}{x+4} \\ & \\ \text{Factor the numerator.} &\dfrac{(x+4)(x+7)}{x+4} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{\cancel{(x+4)}(x+7)}{\cancel{x+4}} \\ & \\ \text{Simplify.} &x+7 \end{array}\)

يتم تبسيط التعبير\(x+7\) ولكن التعبير الأصلي كان له قاسم\(x+4\) لذلك\(x\neq −4\).

جرب ذلك\(\PageIndex{2}\)

قم بالتبسيط:\(\dfrac{9x+14}{x+7}+\dfrac{x^2}{x+7}\).

إجابة

\(x+2\)

جرب ذلك\(\PageIndex{3}\)

قم بالتبسيط:\(\dfrac{x^2+8x}{x+5}+\dfrac{15}{x+5}\).

إجابة

\(x+3\)

لطرح التعبيرات العقلانية، يجب أن يكون لها أيضًا قاسم مشترك. عندما تكون المقامات متماثلة، يمكنك طرح البسط ووضع الفرق على المقام المشترك. احذر من العلامات عند طرح معادلة ذات حدين أو ثلاثية.

مثال\(\PageIndex{4}\)

طرح:\(\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18}\).

الحل

\(\begin{array} {ll} &\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18} \\ & \\ \begin{array} {l} \text{Subtract the numerators and place the} \\ \text{difference over the common denominator.} \end{array} &\dfrac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18} \\ & \\ \text{Distribute the sign in the numerator.} &\dfrac{5x^2−7x+3−4x^2−x+9}{x^2−3x−18} \\ & \\ \text{Combine like terms.} &\dfrac{x^2−8x+12}{x^2−3x−18} \\ & \\ \text{Factor the numerator and the denominator.} &\dfrac{(x−2)(x−6)}{(x+3)(x−6)} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{(x−2)\cancel{(x−6)}}{(x+3)\cancel{(x−6)}} \\ & \\ &(x−2)(x+3) \end{array}\)

جرب ذلك\(\PageIndex{5}\)

طرح:\(\dfrac{4x^2−11x+8}{x^2−3x+2}−\dfrac{3x^2+x−3}{x^2−3x+2}\).

إجابة

\(\dfrac{x−11}{x−2}\)

جرب ذلك\(\PageIndex{6}\)

طرح:\(\dfrac{6x^2−x+20}{x^2−81}−\dfrac{5x^2+11x−7}{x^2−81}\).

إجابة

\(\dfrac{x−3}{x+9}\)

جمع وطرح التعبيرات الكسرية التي مقاماتها أضداد

عندما تكون مقامات تعبيرين عقلانيين متضادتين، فمن السهل الحصول على قاسم مشترك. علينا فقط ضرب أحد الكسور في\(\dfrac{−1}{−1}\).

دعونا نرى كيف يعمل هذا.

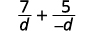اضرب الكسر الثاني في\(\dfrac{−1}{−1}\).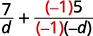
القواسم هي نفسها.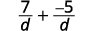
قم بالتبسيط.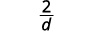

كن حذرًا مع العلامات أثناء التعامل مع الأضداد عندما يتم طرح الكسور.

مثال\(\PageIndex{7}\)

طرح:\(\dfrac{m^2−6m}{m^2−1}−\dfrac{3m+2}{1−m^2}\).

الحل

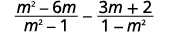المقامات هي الأضداد، لذا اضرب الكسر الثاني في\(\dfrac{−1}{−1}\).
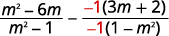قم بتبسيط الكسر الثاني.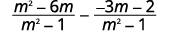
القواسم هي نفسها. اطرح البسط.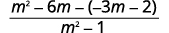
توزيع.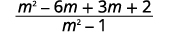
اجمع بين المصطلحات المتشابهة.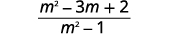
عامل البسط والمقام.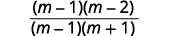
قم بالتبسيط من خلال إزالة العوامل المشتركة.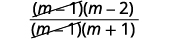
قم بالتبسيط.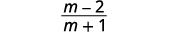

جرب ذلك\(\PageIndex{8}\)

طرح:\(\dfrac{y^2−5y}{y^2−4}−\dfrac{6y−6}{4−y^2}\).

إجابة

\(\dfrac{y+3}{y+2}\)

جرب ذلك\(\PageIndex{9}\)

طرح:\(\dfrac{2n^2+8n−1}{n^2−1}−\dfrac{n^2−7n−1}{1−n^2}\).

إجابة

\(\dfrac{3n−2}{n−1}\)

أوجد المقام المشترك الأصغر للمقادير الكسرية

عندما نجمع أو نطرح مقادير كسرية ذات مقامات مختلفة، سنحتاج إلى الحصول على مقامات مشتركة. إذا راجعنا الإجراء الذي استخدمناه مع الكسور العددية، فسوف نعرف ما يجب فعله مع التعبيرات النسبية.

لنلقِ نظرة على هذا المثال:\(\dfrac{7}{12}+\dfrac{5}{18}\). نظرًا لأن القواسم ليست هي نفسها، كانت الخطوة الأولى هي العثور على القاسم المشترك الأصغر (LCD).

للعثور على شاشة LCD الخاصة بالكسور، قمنا بأخذ 12 و 18 في الاعتبار في الأعداد الأولية، وقمنا بترتيب أي أعداد أولية شائعة في الأعمدة. ثم قمنا «بإسقاط» جزء أساسي واحد من كل عمود. أخيرًا، قمنا بضرب العوامل للعثور على شاشة LCD.

عندما نضيف الكسور العددية، بمجرد العثور على شاشة LCD، نعيد كتابة كل كسر في صورة كسر مكافئ لشاشة LCD بضرب البسط والمقام في نفس الرقم. نحن الآن جاهزون للإضافة.

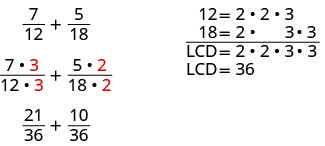
نحن نفعل نفس الشيء للتعبيرات العقلانية. ومع ذلك، نترك شاشة LCD في شكل معمول.

أوجد القاسم المشترك الأصغر للمقادير الكسرية.

1. ضع كل قاسم في الاعتبار تمامًا.
2. ضع قائمة بعوامل كل قاسم. عوامل المطابقة عموديًا عندما يكون ذلك ممكنًا.
3. قم بإسقاط الأعمدة من خلال تضمين جميع العوامل، ولكن لا تتضمن العوامل المشتركة مرتين.
4. اكتب شاشة LCD كمنتج للعوامل.

تذكر أننا نستبعد دائمًا القيم التي تجعل المقام صفرًا. ما قيم xx التي يجب أن نستبعدها في المثال التالي؟

مثال\(\PageIndex{10}\)

أ. ابحث عن شاشة LCD للتعبيرات\(\dfrac{8}{x^2−2x−3}\)،\(\dfrac{3x}{x^2+4x+3}\) ب. أعد كتابتها كتعبيرات نسبية مكافئة ذات قاسم مشترك أدنى.

الحل

أ.

ابحث عن شاشة LCD لـ\(\dfrac{8}{x^2−2x−3}\),\(\dfrac{3x}{x^2+4x+3}\).
ضع كل قاسم في الاعتبار بشكل كامل، واصطف العوامل المشتركة. انزل الأعمدة.
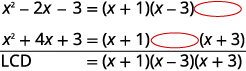اكتب شاشة LCD كمنتج للعوامل.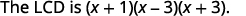

ب.

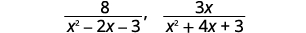ضع في اعتبارك كل قاسم.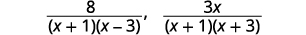
اضرب كل قاسم في عامل شاشة LCD «المفقود» واضرب كل عداد بنفس العامل.
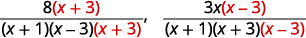قم بتبسيط البسط.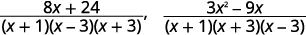

جرب ذلك\(\PageIndex{11}\)

أ. ابحث عن شاشة LCD للتعبيرات\(\dfrac{2}{x^2−x−12}\)،\(\dfrac{1}{x^2−16}\) ب. أعد كتابتها كتعبيرات نسبية مكافئة ذات قاسم مشترك أصغر.

إجابة

أ.\((x−4)(x+3)(x+4)\)
ب.\(\dfrac{2x+8}{(x−4)(x+3)(x+4)}\)،
\(\dfrac{x+3}{(x−4)(x+3)(x+4)}\)

جرب ذلك\(\PageIndex{12}\)

أ. ابحث عن شاشة LCD للتعبيرات\(\dfrac{3x}{x^2−3x+10}\)،\(\dfrac{5}{x^2+3x+2}\) ب. أعد كتابتها كتعبيرات نسبية مكافئة ذات قاسم مشترك أصغر.

إجابة

أ.\((x+2)(x−5)(x+1)\)
ب.\(\dfrac{3x^2+3x}{(x+2)(x−5)(x+1)}\)،
\(\dfrac{5x−25}{(x+2)(x−5)(x+1)}\)

جمع وطرح المقادير الكسرية ذات المقامات المختلفة

الآن لدينا جميع الخطوات التي نحتاجها لإضافة أو طرح التعبيرات العقلانية ذات المقامات المختلفة.

مثال\(\PageIndex{13}\): How to Add Rational Expressions with Unlike Denominators

إضافة:\(\dfrac{3}{x−3}+\dfrac{2}{x−2}\).

الحل

جرب ذلك\(\PageIndex{14}\)

إضافة:\(\dfrac{2}{x−2}+\dfrac{5}{x+3}\).

إجابة

\(\dfrac{7x−4}{(x−2)(x+3)}\)

جرب ذلك\(\PageIndex{15}\)

إضافة:\(\dfrac{4}{m+3}+\dfrac{3}{m+4}\).

إجابة

\(\dfrac{7m+25}{(m+3)(m+4)}\)

يتم تلخيص الخطوات المستخدمة لإضافة التعبيرات المنطقية هنا.

قم بإضافة التعبيرات العقلانية أو طرحها.

1. حدِّد ما إذا كانت المقادير تحتوي على قاسم مشترك.
   • نعم - انتقل إلى الخطوة 2.
   • لا - أعد كتابة كل تعبير منطقي باستخدام شاشة LCD.
     • ابحث عن شاشة LCD.
     • أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.
2. قم بإضافة التعبيرات العقلانية أو طرحها.
3. قم بالتبسيط، إن أمكن.

تجنب إغراء التبسيط في وقت مبكر جدًا. في المثال أعلاه، يجب أن نترك التعبير العقلاني الأول\(\dfrac{3x−6}{(x−3)(x−2)}\) حتى نتمكن من إضافته إليه\(\dfrac{2x−6}{(x−2)(x−3)}\). قم بالتبسيط فقط بعد دمج البسط.

مثال\(\PageIndex{16}\)

إضافة:\(\dfrac{8}{x^2−2x−3}+\dfrac{3x}{x^2+4x+3}\).

الحل

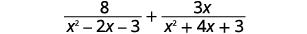هل تحتوي التعبيرات على قاسم مشترك؟	لا.
أعد كتابة كل تعبير باستخدام شاشة LCD.
\(\begin{array} {ll} & \\ & \\ \text{Find the LCD.} &\begin{array} {l} \hspace{5mm} x^2−2x−3=(x+1)(x−3) \\ \underline{x^2+4x+3=(x+1)\quad (x+3)} \\ & \\ \qquad LCD=(x+1)(x−3)(x+3) \end{array} \end{array} \)
أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.
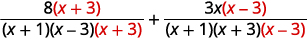قم بتبسيط البسط.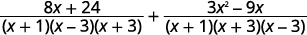
أضف التعبيرات العقلانية.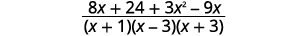
قم بتبسيط البسط.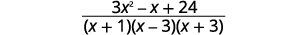
	البسط أساسي، لذلك لا توجد عوامل مشتركة.

جرب ذلك\(\PageIndex{17}\)

إضافة:\(\dfrac{1}{m^2−m−2}+\dfrac{5m}{m^2+3m+2}\).

إجابة

\(\dfrac{5m^2−9m+2}{(m+1)(m−2)(m+2)}\)

جرب ذلك\(\PageIndex{18}\)

إضافة:\(\dfrac{2n}{n^2−3n−10}+\dfrac{6}{n^2+5n+6}\).

إجابة

\(\dfrac{2n^2+12n−30}{(n+2)(n−5)(n+3)}\)

العملية التي نستخدمها لطرح التعبيرات الكسرية ذات المقامات المختلفة هي نفسها المستخدمة في الجمع. علينا فقط أن نكون حذرين للغاية من العلامات عند طرح البسط.

مثال\(\PageIndex{19}\)

طرح:\(\dfrac{8y}{y^2−16}−\dfrac{4}{y−4}\).

الحل

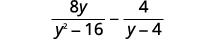هل تحتوي التعبيرات على قاسم مشترك؟	لا.
أعد كتابة كل تعبير باستخدام شاشة LCD.
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} y^2−16=(y−4)(y+4) \\ \quad \underline{y−4=y−4} \\ LCD=(y−4)(y+4) \end{array} \end{array} \)
أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.
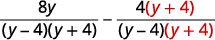قم بتبسيط البسط.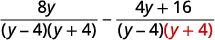
اطرح التعبيرات النسبية.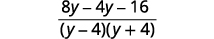
قم بتبسيط البسط.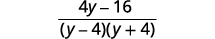
ضع البسط في الاعتبار للبحث عن العوامل المشتركة.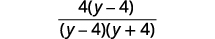
إزالة العوامل المشتركة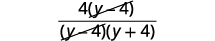
قم بالتبسيط.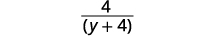

جرب ذلك\(\PageIndex{20}\)

طرح:\(\dfrac{2x}{x^2−4}−\dfrac{1}{x+2}\).

إجابة

\(\dfrac{1}{x−2}\)

جرب ذلك\(\PageIndex{21}\)

طرح:\(\dfrac{3}{z+3}−\dfrac{6z}{z^2−9}\).

إجابة

\(\dfrac{−3}{z−3}\)

هناك الكثير من العلامات السلبية في المثال التالي. كن حذرًا جدًا.

مثال\(\PageIndex{22}\)

طرح:\(\dfrac{−3n−9}{n^2+n−6}−\dfrac{n+3}{2−n}\).

الحل

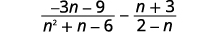عامل المقام.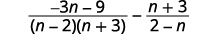
بما\(n−2\)\(2−n\) أننا متضادان، فإننا سنضرب التعبير العقلاني الثاني بـ\(\dfrac{−1}{−1}\).
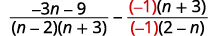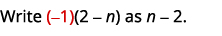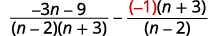قم بالتبسيط. تذكر،\(a−(−b)=a+b\).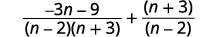
هل المقادير الكسرية لها قاسم مشترك؟ لا.
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} n^2+n−6=(n−2)(n+3) \\ \quad\underline{n−2=(n−2)} \\ LCD=\quad (n−2)(n+3) \end{array} \end{array} \)
أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.
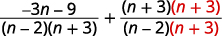قم بتبسيط البسط.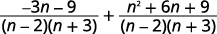
أضف التعبيرات العقلانية.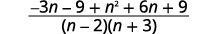
قم بتبسيط البسط.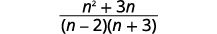
ضع البسط في الاعتبار للبحث عن العوامل المشتركة.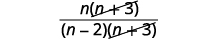
قم بالتبسيط.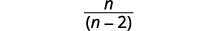

جرب ذلك\(\PageIndex{23}\)

طرح:\(\dfrac{3x−1}{x^2−5x−6}−\dfrac{2}{6−x}\).

إجابة

\(\dfrac{5x+1}{(x−6)(x+1)}\)

جرب ذلك\(\PageIndex{24}\)

طرح:\(\dfrac{−2y−2}{y^2+2y−8}−\dfrac{y−1}{2−y}\).

إجابة

\(\dfrac{y+3}{y+4}\)

يمكن أن تصبح الأمور فوضوية للغاية عندما يجب ضرب كلا الكسرين في حدين للحصول على القاسم المشترك.

مثال\(\PageIndex{25}\)

طرح:\(\dfrac{4}{a^2+6a+5}−\dfrac{3}{a^2+7a+10}\).

الحل

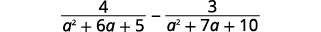ضع القواسم في الاعتبار.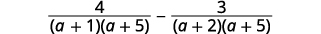
هل المقادير الكسرية لها قاسم مشترك؟ لا.
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} a^2+6a+5=(a+1)(a+5) \\ \underline{a^2+7a+10=(a+5)(a+2)} \\ LCD=(a+1)(a+5)(a+2) \end{array} \end{array} \)
أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.
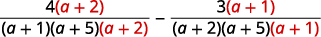قم بتبسيط البسط.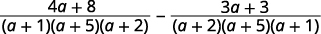
اطرح التعبيرات النسبية.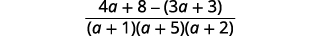
قم بتبسيط البسط.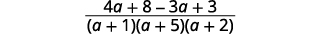
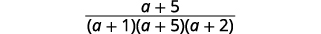ابحث عن العوامل المشتركة.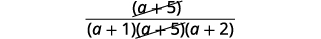
قم بالتبسيط.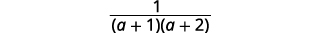

جرب ذلك\(\PageIndex{26}\)

طرح:\(\dfrac{3}{b^2−4b−5}−\dfrac{2}{b^2−6b+5}\).

إجابة

\(\dfrac{1}{(b+1)(b−1)}\)

جرب ذلك\(\PageIndex{27}\)

طرح:\(\dfrac{4}{x^2−4}−\dfrac{3}{x^2−x−2}\).

إجابة

\(\dfrac{1}{(x+2)(x+1)}\)

نتبع نفس الخطوات السابقة للعثور على شاشة LCD عندما يكون لدينا أكثر من تعبيرين منطقيين. في المثال التالي، سنبدأ بحساب جميع القواسم الثلاثة للعثور على شاشة LCD الخاصة بها.

مثال\(\PageIndex{28}\)

قم بالتبسيط:\(\dfrac{2u}{u−1}+\dfrac{1}{u}−\dfrac{2u−1}{u^2−u}\).

الحل

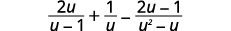هل تحتوي التعبيرات على قاسم مشترك؟ لا. أعد كتابة كل تعبير باستخدام شاشة LCD.
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} u−1=(u−1) \\ u=u \\ \underline{u^2−u=u(u−1)} \\ LCD=u(u−1) \end{array} \end{array}\)
أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.
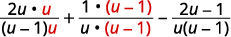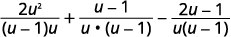اكتب كتعبير منطقي واحد.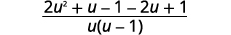
قم بالتبسيط.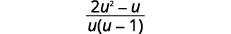
ضع البسط في الاعتبار وأزل العوامل المشتركة.
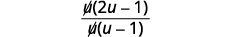قم بالتبسيط.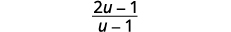

جرب ذلك\(\PageIndex{29}\)

قم بالتبسيط:\(\dfrac{v}{v+1}+\dfrac{3}{v−1}−\dfrac{6}{v^2−1}\).

إجابة

\(\dfrac{v+3}{v+1}\)

جرب ذلك\(\PageIndex{30}\)

قم بالتبسيط:\(\dfrac{3w}{w+2}+\dfrac{2}{w+7}−\dfrac{17w+4}{w^2+9w+14}\).

إجابة

\(\dfrac{3w}{w+7}\)

جمع وطرح الدوال الكسرية

لجمع الدوال الكسرية أو طرحها، نستخدم نفس الأساليب التي استخدمناها لإضافة أو طرح دوال كثيرة الحدود.

مثال\(\PageIndex{31}\)

ابحث عن\(R(x)=f(x)−g(x)\) المكان\(f(x)=\dfrac{x+5}{x−2}\) و\(g(x)=\dfrac{5x+18}{x^2−4}\).

حل

بديل في الوظائف\(f(x)\)،\(g(x)\).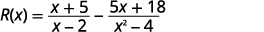
ضع القواسم في الاعتبار.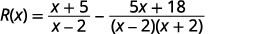
هل تحتوي التعبيرات على قاسم مشترك؟ لا. أعد كتابة كل تعبير باستخدام شاشة LCD.
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} x−2=(x−2) \\ \underline{x^2−4=(x−2)(x+2)} \\ \hspace{4mm} LCD=(x−2)(x+2)\end{array} \end{array}\)
أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.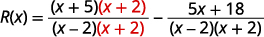
اكتب كتعبير منطقي واحد.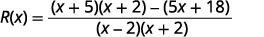
قم بالتبسيط.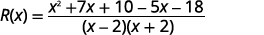
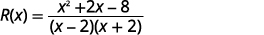
ضع البسط في الاعتبار وأزل العوامل المشتركة.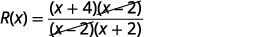
قم بالتبسيط.

جرب ذلك\(\PageIndex{32}\)

ابحث عن\(R(x)=f(x)−g(x)\) المكان\(f(x)=\dfrac{x+1}{x+3}\) و\(g(x)=\dfrac{x+17}{x^2−x−12}\).

إجابة

\(\dfrac{x−7}{x−4}\)

جرب ذلك\(\PageIndex{33}\)

ابحث عن\(R(x)=f(x)+g(x)\) المكان\(f(x)=\dfrac{x−4}{x+3}\) و\(g(x)=\dfrac{4x+6}{x^2−9}\).

إجابة

\(\dfrac{x^2−3x+18}{(x+3)(x−3)}\)

قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع إضافة التعبيرات العقلانية وطرحها.

• جمع وطرح التعبيرات الكسرية - المقامات غير المتشابهة

المفاهيم الرئيسية

• الجمع والطرح للتعبير العقلاني
  إذا كانت\(p\)\(r\) وكثيرات الحدود\(r\neq 0\)، وأين، إذن\(q\)
  \[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\]
• كيفية العثور على القاسم المشترك الأصغر للتعبيرات العقلانية.
  1. ضع في اعتبارك كل تعبير تمامًا.
  2. ضع قائمة بعوامل كل تعبير. عوامل المطابقة عموديًا عندما يكون ذلك ممكنًا.
  3. انزل الأعمدة.
  4. اكتب شاشة LCD كمنتج للعوامل.
• كيفية إضافة أو طرح التعبيرات العقلانية.
  1. حدِّد ما إذا كانت المقادير تحتوي على قاسم مشترك.
     • نعم - انتقل إلى الخطوة 2.
     • لا - أعد كتابة كل تعبير منطقي باستخدام شاشة LCD.
       • ابحث عن شاشة LCD.
       • أعد كتابة كل تعبير منطقي كتعبير عقلاني مكافئ باستخدام شاشة LCD.
  2. قم بإضافة التعبيرات العقلانية أو طرحها.
  3. قم بالتبسيط، إن أمكن.