6.6: معادلات كثيرة الحدود
- Page ID
- 201538
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم خاصية المنتج الصفري
- حل المعادلات التربيعية عن طريق التحليل
- حل المعادلات ذات الدوال الكثيرة الحدود
- حل تطبيقات نموذجية باستخدام معادلات كثيرة الحدود
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
لقد أمضينا وقتًا طويلاً في تعلم كيفية حساب كثيرات الحدود. سننظر الآن في المعادلات كثيرة الحدود ونحلها باستخدام التحليل، إن أمكن.
معادلة كثيرة الحدود هي معادلة تحتوي على تعبير متعدد الحدود. درجة المعادلة كثيرة الحدود هي درجة كثيرة الحدود.
معادلة كثيرة الحدود هي معادلة تحتوي على تعبير متعدد الحدود.
درجة المعادلة كثيرة الحدود هي درجة كثيرة الحدود.
لقد قمنا بالفعل بحل المعادلات متعددة الحدود من الدرجة الأولى. المعادلات كثيرة الحدود من الدرجة الأولى هي معادلات خطية من الشكل\(ax+b=c\).
سنقوم الآن بحل معادلات كثيرة الحدود من الدرجة الثانية. تُسمى المعادلة الكثيرة الحدود من الدرجة الثانية بالمعادلة التربيعية. فيما يلي بعض الأمثلة على المعادلات التربيعية:
\[x^2+5x+6=0 \qquad 3y^2+4y=10 \qquad 64u^2−81=0 \qquad n(n+1)=42 \nonumber\]
لا يبدو أن المعادلة الأخيرة تحتوي على متغير مربع، ولكن عندما نبسط التعبير على اليسار سنحصل عليه\(n^2+n\).
الشكل العام للمعادلة التربيعية هو\(ax^2+bx+c=0\)، مع\(a\neq 0\). (إذا\(a=0\)، إذن\(0·x^2=0\)، ولم يتبق لنا حد تربيعي.)
تُسمى معادلة الشكل\(ax^2+bx+c=0\) بالمعادلة التربيعية.
\[a,b,\text{ and }c\text{ are real numbers and }a\neq 0\nonumber\]
لحل المعادلات التربيعية، نحتاج إلى طرق مختلفة عن تلك التي استخدمناها في حل المعادلات الخطية. سننظر إلى طريقة واحدة هنا ثم عدة طرق أخرى في فصل لاحق.
استخدم خاصية المنتج الصفري
سنقوم أولاً بحل بعض المعادلات التربيعية باستخدام خاصية المنتج الصفري. تقول خاصية Zero Product أنه إذا كان منتج الكميتين صفرًا، فإن واحدة على الأقل من الكميات هي صفر. الطريقة الوحيدة للحصول على منتج يساوي الصفر هي الضرب في الصفر نفسه.
إذا\(a·b=0\)، ثم إما\(a=0\)\(b=0\) أو كليهما.
سنستخدم الآن خاصية المنتج الصفري لحل المعادلة التربيعية.
حل:\((5n−2)(6n−1)=0\).
- إجابة
-



حل:\((3m−2)(2m+1)=0\).
- إجابة
-
\(m=\frac{2}{3},\space m=−\frac{1}{2}\)
حل:\((4p+3)(4p−3)=0\).
- إجابة
-
\(p=−\frac{3}{4},\space p=\frac{3}{4}\)
- اضبط كل عامل مساويًا للصفر.
- حل المعادلات الخطية.
- تحقق.
حل المعادلات التربيعية عن طريق التحليل
تعمل خاصية المنتج الصفري بشكل جيد جدًا لحل المعادلات التربيعية. يجب أخذ المعادلة التربيعية في الاعتبار، مع عزل الصفر على جانب واحد. لذلك نتأكد من البدء بالمعادلة التربيعية في الشكل القياسي،\(ax^2+bx+c=0\). ثم نقوم بحساب التعبير على اليسار.
حل:\(2y^2=13y+45\).
- إجابة
-

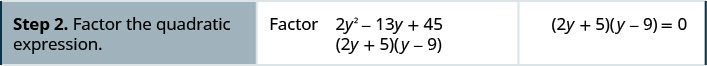


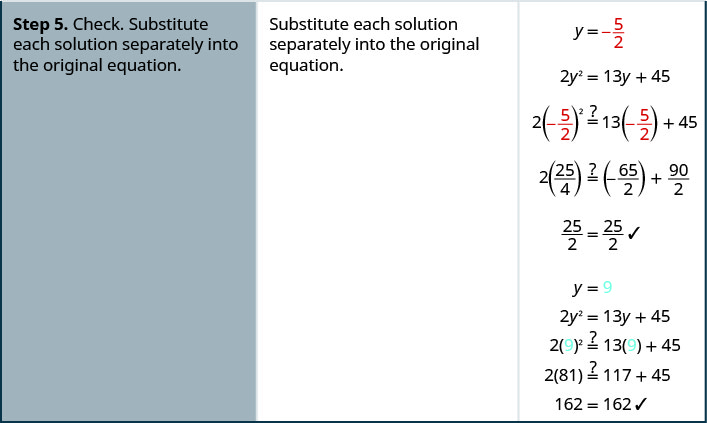
حل:\(3c^2=10c−8\).
- إجابة
-
\(c=2,\space c=\frac{4}{3}\)
حل:\(2d^2−5d=3\).
- إجابة
-
\(d=3,\space d=−12\)
- اكتب المعادلة التربيعية في الصورة القياسية،\(ax^2+bx+c=0\).
- عامِل التعبير التربيعي.
- استخدم خاصية المنتج الصفري.
- حل المعادلات الخطية.
- تحقق. استبدل كل حل على حدة في المعادلة الأصلية.
قبل إجراء التحليل، يجب أن نتأكد من أن المعادلة التربيعية في الصورة القياسية.
سيؤدي حل المعادلات التربيعية عن طريق التحليل إلى الاستفادة من جميع تقنيات العوملة التي تعلمتها في هذا الفصل! هل تتعرف على نمط المنتج الخاص في المثال التالي؟
حل:\(169q^2=49\).
- إجابة
-
\(\begin{array} {ll} &169x^2=49 \\ \text{Write the quadratic equation in standard form.} &169x^2−49=0 \\ \text{Factor. It is a difference of squares.} &(13x−7)(13x+7)=0 \\ \text{Use the Zero Product Property to set each factor to }0. & \\ \text{Solve each equation.} &\begin{array} {ll} 13x−7=0 &13x+7=0 \\ 13x=7 &13x=−7 \\ x=\frac{7}{13} &x=−\frac{7}{13} \end{array} \end{array}\)
تحقق من:
نترك الفحص لك.
حل:\(25p^2=49\).
- إجابة
-
\(p=\frac{7}{5},p=−\frac{7}{5}\)
حل:\(36x^2=121\).
- إجابة
-
\(x=\frac{11}{6},x=−\frac{11}{6}\)
في المثال التالي، يتم أخذ الجانب الأيسر من المعادلة في الاعتبار، ولكن الجانب الأيمن ليس صفرًا. من أجل استخدام خاصية Zero Product، يجب أن يكون أحد طرفي المعادلة صفرًا. سنضرب العوامل ثم نكتب المعادلة في الصورة القياسية.
حل:\((3x−8)(x−1)=3x\).
- إجابة
-
\(\begin{array} {ll} &(3x−8)(x−1)=3x \\ \text{Multiply the binomials.} &3x^2−11x+8=3x \\ \text{Write the quadratic equation in standard form.} &3x^2−14x+8=0 \\ \text{Factor the trinomial.} &(3x−2)(x−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {ll} 3x−2=0 &x−4=0 \\ 3x=2 &x=4 \\ x=\frac{2}{3} & \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
حل:\((2m+1)(m+3)=12m\).
- إجابة
-
\(m=1,\space m=\frac{3}{2}\)
حل:\((k+1)(k−1)=8\).
- إجابة
-
\(k=3,\space k=−3\)
في المثال التالي، عندما نحلل المعادلة التربيعية سنحصل على ثلاثة عوامل. لكن العامل الأول ثابت. نحن نعلم أن هذا العامل لا يمكن أن يساوي 0.
حل:\(3x^2=12x+63\).
- إجابة
-
\(\begin{array} {ll} &3x^2=12x+63 \\ \text{Write the quadratic equation in standard form.} &3x^2−12x−63=0 \\ \text{Factor the greatest common factor first.} &3(x^2−4x−21)=0 \\ \text{Factor the trinomial.} &3(x−7)(x+3)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {lll} 3\neq 0 &x−7=0 &x+3=0 \\ 3\neq 0 &x=7 &x=−3 \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
حل:\(18a^2−30=−33a\).
- إجابة
-
\(a=−\frac{5}{2},a=\frac{2}{3}\)
حل:\(123b=−6−60b^2\)
- إجابة
-
\(b=−2,\space b=−\frac{1}{20}\)
تنطبق خاصية Zero Product أيضًا على المنتج المكون من ثلاثة عوامل أو أكثر. إذا كان المنتج صفرًا، يجب أن يكون أحد العوامل على الأقل صفرًا. يمكننا حل بعض المعادلات بدرجة أكبر من درجتين باستخدام خاصية المنتج الصفري، تمامًا كما قمنا بحل المعادلات التربيعية.
حل:\(9m^3+100m=60m^2\)
- إجابة
-
\(\begin{array} {ll} & 9m^3+100m=60m^2 \\ \text{Bring all the terms to one side so that the other side is zero.} &9m^3−60m^2+100m=0 \\ \text{Factor the greatest common factor first.} &m(9m^2−60m+100)=0 \\ \text{Factor the trinomial.} &m(3m−10)^2=0 \end{array}\\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} &\begin{array} {lll} m=0 &3m−10=0 &{}\\ m=0 &m=\frac{10}{3} & {} \end{array}\\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
حل:\(8x^3=24x^2−18x\).
- إجابة
-
\(x=0,\space x=\frac{3}{2}\)
حل:\(16y^2=32y^3+2y\).
- إجابة
-
\(y=0,\space y=14\)
حل المعادلات ذات الدوال الكثيرة الحدود
مع استمرار دراستنا للدوال كثيرة الحدود، سيكون من المهم غالبًا معرفة متى سيكون للدالة قيمة معينة أو النقاط الموجودة على الرسم البياني للدالة. سيساعدنا عملنا مع خاصية Zero Product في العثور على هذه الإجابات.
بالنسبة للوظيفة\(f(x)=x^2+2x−2\)،
ⓐ ابحث عن\(x\) وقت\(f(x)=6\)
ⓑ ابحث عن نقطتين تقعان على الرسم البياني للدالة.
- إجابة
-
ⓐ
\(\begin{array} {ll} &f(x)=x^2+2x−2 \\ \text{Substitute }6\text{ for }f(x). &6=x^2+2x−2 \\ \text{Put the quadratic in standard form.} &x^2+2x−8=0 \\ \text{Factor the trinomial.} &(x+4)(x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &x−2=0 \\ x=−4 &\text{or} &x=2 \end{array} \\ \text{Check:} & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ \begin{array} {lll} \quad &\hspace{3mm} f(x)=x^2+2x−2 &f(x)=x^2+2x−2 \\ \quad &f(−4)=(−4)^2+2(−4)−2 &f(2)=2^2+2·2−2 \\ \quad &f(−4)=16−8−2 &f(2)=4+4−2 \\ \quad &f(−4)=6\checkmark &f(2)=6\checkmark \end{array} & \end{array} \)
ⓑ منذ ذلك الحين\(f(−4)=6\)\(f(2)=6\)،\((2,6)\) تكمن النقاط\((−4,6)\) والنقاط على الرسم البياني للدالة.
بالنسبة للوظيفة\(f(x)=x^2−2x−8\)،
ⓐ ابحث عن\(x\) الوقت\(f(x)=7\)
ⓑ ابحث عن نقطتين تقعان على الرسم البياني للدالة.
- إجابة
-
ⓐ\(x=−3\) أو\(x=5\)
ⓑ\((−3,7)\space (5,7)\)
بالنسبة للوظيفة\(f(x)=x^2−8x+3\)،
ⓐ ابحث عن\(x\) الوقت\(f(x)=−4\)
ⓑ ابحث عن نقطتين تقعان على الرسم البياني للدالة.
- إجابة
-
ⓐ\(x=1\) أو\(x=7\)
ⓑ\((1,−4)\space (7,−4)\)
تساعدنا خاصية Zero Product أيضًا في تحديد مكان الوظيفة صفر. تُسمى قيمة\(x\) مكان\(0\) الدالة صفرًا للدالة.
بالنسبة لأي وظيفة\(f\)، إذا كانت\(f(x)=0\)، إذن،\(x\) تساوي صفرًا للدالة.
عندما تكون\(f(x)=0\) النقطة\((x,0)\) هي نقطة على الرسم البياني. هذه النقطة هي\(x\) نقطة تقاطع للرسم البياني. غالبًا ما يكون من المهم معرفة مكان تقاطع الرسم البياني للدالة مع المحاور. سنرى بعض الأمثلة لاحقًا.
للحصول على الوظيفة\(f(x)=3x^2+10x−8\)، ابحث
ⓐ أصفار الدالة،
ⓑ أي\(x\) - تقاطعات من الرسم البياني للدالة
ⓒ أي\(y\) - تقاطعات من الرسم البياني للدالة
- إجابة
-
ⓐ للعثور على أصفار الدالة، نحتاج إلى معرفة متى تكون قيمة الدالة 0.
\(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Substitute }0\text{ for}f(x). &0=3x^2+10x−8 \\ \text{Factor the trinomial.} &(x+4)(3x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &3x−2=0 \\ x=−4 &\text{or} &x=\frac{2}{3} \end{array} \end{array}\)
ⓑ يحدث\(x\) الاعتراض عند حدوث ذلك\(y=0\). منذ ذلك الحين\(f(−4)=0\)\(f(\frac{2}{3})=0\)،\((\frac{2}{3},0)\) تكمن النقاط\((−4,0)\) والنقاط على الرسم البياني. هذه النقاط عبارة\(x\) عن نقاط تقاطع للدالة.
ⓒ يحدث\(y\) التقاطع عند حدوث ذلك\(x=0\). للعثور على\(y\) نقاط الاعتراض التي نحتاج إلى العثور عليها\(f(0)\).
\(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Find }f(0)\text{ by substituting }0\text{ for }x. &f(0)=3·0^2+10·0−8 \\ \text{Simplify.} &f(0)=−8 \end{array} \)
نظرًا لأن\(f(0)=−8\) النقطة\((0,−8)\) تكمن في الرسم البياني. هذه النقطة هي\(y\) التقاطع - للدالة.
للحصول على الوظيفة\(f(x)=2x^2−7x+5\)، ابحث
ⓐ أصفار الدالة
ⓑ أي\(x\) - تقاطعات من الرسم البياني للدالة
ⓒ أي\(y\) - تقاطعات من الرسم البياني للدالة.
- إجابة
-
ⓐ\(x=1\) أو\(x=\frac{5}{2}\)
ⓑ\((1,0),\space (\frac{5}{2},0)\) ⓒ\((0,5)\)
للحصول على الوظيفة\(f(x)=6x^2+13x−15\)، ابحث
ⓐ أصفار الدالة
ⓑ أي\(x\) - تقاطعات من الرسم البياني للدالة
ⓒ أي\(y\) - تقاطعات من الرسم البياني للدالة.
- إجابة
-
ⓐ\(x=−3\) أو\(x=\frac{5}{6}\)
ⓑ\((−3,0),\space (\frac{5}{6},0)\) ⓒ\((0,−15)\)
حل تطبيقات نموذجية باستخدام معادلات كثيرة الحدود
ستعمل إستراتيجية حل المشكلات التي استخدمناها سابقًا للتطبيقات التي تترجم إلى معادلات خطية تمامًا مع التطبيقات التي تترجم إلى معادلات كثيرة الحدود. سنقوم بنسخ استراتيجية حل المشكلات هنا حتى نتمكن من استخدامها كمرجع.
- اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
- حدد ما نبحث عنه.
- اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
- ترجم إلى معادلة. قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة الإنجليزية إلى معادلة جبرية.
- حل المعادلة باستخدام تقنيات الجبر المناسبة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
سنبدأ بمشكلة عددية للتدرب على ترجمة الكلمات إلى معادلة كثيرة الحدود.
حاصل ضرب عددين صحيحين فرديين متتاليين هو 323. ابحث عن الأعداد الصحيحة.
- إجابة
-
\(\begin{array} {ll} \textbf{Step 1. Read }\text{the problem.} & \\ \textbf{Step 2. Identify }\text{what we are looking for.} &\text{We are looking for two consecutive integers.} \\ \textbf{Step 3. Name}\text{ what we are looking for.} &\text{Let } n=\text{ the first integer.} \\ &n+2= \text{ next consecutive odd integer} \\ \begin{array} {l} \textbf{Step 4. Translate }\text{into an equation. Restate the}\hspace{20mm} \\ \text{problem in a sentence.} \end{array} &\begin{array} {l} \text{The product of the two consecutive odd} \\ \text{integers is }323. \end{array} \\ &\quad n(n+2)=323 \\ \textbf{Step 5. Solve }\text{the equation.} n^2+2n=323 \\ \text{Bring all the terms to one side.} &n^2+2n−323=0 \\ \text{Factor the trinomial.} &(n−17)(n+19)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve the equations.} \end{array} &\begin{array} {ll} n−17=0 \hspace{10mm}&n+19=0 \\ n=17 &n=−19 \end{array} \end{array} \)
هناك قيمتان\(n\) لذلك وهما حلول لهذه المشكلة. لذلك هناك مجموعتان من الأعداد الصحيحة الفردية المتتالية التي ستعمل.\(\begin{array} {ll} \text{If the first integer is } n=17 \hspace{60mm} &\text{If the first integer is } n=-19 \\ \text{then the next odd integer is} &\text{then the next odd integer is} \\ \hspace{53mm} n+2 &\hspace{53mm} n+2 \\ \hspace{51mm} 17+2 &\hspace{51mm} -19+2 \\ \hspace{55mm} 19 &\hspace{55mm} -17 \\ \hspace{51mm} 17,19 &\hspace{51mm} -17,-19 \\ \textbf{Step 6. Check }\text{the answer.} & \\ \text{The results are consecutive odd integers} & \\ \begin{array} {ll} 17,\space 19\text{ and }−19,\space −17. & \\ 17·19=323\checkmark &−19(−17)=323\checkmark \end{array} & \\ \text{Both pairs of consecutive integers are solutions.} & \\ \textbf{Step 7. Answer }\text{the question} &\text{The consecutive integers are }17, 19\text{ and }−19,−17. \end{array} \)
حاصل ضرب عددين صحيحين فرديين متتاليين هو 255. ابحث عن الأعداد الصحيحة.
- إجابة
-
\(−15,−17\)و\(15, 17\)
حاصل ضرب عددين صحيحين فرديين متتاليين هو 483 أوجد الأعداد الصحيحة.
- إجابة
-
\(−23,−21\)و\(21, 23\)
هل فوجئت بزوج الأعداد الصحيحة السالبة الذي يعد أحد الحلول للمثال السابق؟ يعطي كل من ناتج العددين الصحيحين الموجبين ومنتج العددين الصحيحين السالبين نتائج إيجابية.
في بعض التطبيقات، ستنتج الحلول السلبية عن الجبر، ولكنها لن تكون واقعية بالنسبة للحالة.
تبلغ مساحة غرفة النوم المستطيلة 117 قدمًا مربعًا. يبلغ طول غرفة النوم أربعة أقدام أكثر من العرض. ابحث عن طول وعرض غرفة النوم.
- إجابة
-
الخطوة 1. اقرأ المشكلة. في المشكلات التي تتضمن أشكالًا
هندسية، يمكن أن يساعدك الرسم
على تصور الموقف.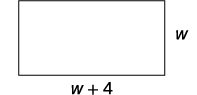
الخطوة 2. حدد ما تبحث عنه. نحن نبحث عن الطول والعرض. الخطوة 3. قم بتسمية ما تبحث عنه. دعونا\(w=\text{ the width of the bedroom}\). الطول يزيد بأربعة أقدام عن العرض. \(w+4=\text{ the length of the garden}\) الخطوة 4. ترجم إلى معادلة. أعد ذكر المعلومات المهمة في الجملة. تبلغ مساحة غرفة النوم 117 قدمًا مربعًا. استخدم الصيغة الخاصة بمساحة المستطيل. \(A=l·w\) استبدل في المتغيرات. \(117=(w+4)w\) الخطوة 5. حل معادلة التوزيع أولاً. \(117=w^2+4w\) احصل على صفر على جانب واحد. \(117=w^2+4w\) عامل ثلاثي الحدود. \(0=w^2+4w−117\) استخدم خاصية المنتج الصفري. \(0=(w^2+13)(w−9)\) حل كل معادلة. \(0=w+13\quad 0=w−9\) \(w\)نظرًا لعرض غرفة النوم، فليس من
المنطقي أن تكون سلبية. نحن نزيل هذه القيمة لـ\(w\).\(\cancel{w=−13}\)\(\quad w=9\) \(w=9\)العرض هو 9 أقدام. أوجد قيمة الطول. \(w+4\)
\(9+4\)
13 الطول هو 13 قدمًا.الخطوة 6. تحقق من الإجابة.
هل الإجابة منطقية؟
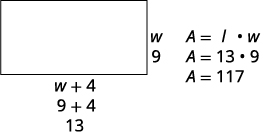
نعم، هذا أمر منطقي.الخطوة 7. أجب على السؤال. يبلغ عرض غرفة النوم 9 أقدام والطول
13 قدمًا.
اللافتة المستطيلة مساحتها 30 قدمًا مربعًا. طول العلامة يزيد بمقدار قدم واحدة عن العرض. ابحث عن طول وعرض العلامة.
- إجابة
-
العرض هو 5 أقدام والطول هو 6 أقدام.
فناء مستطيل بمساحة 180 قدم مربع. عرض الفناء أقل بثلاثة أقدام من الطول. ابحث عن طول وعرض الفناء.
- إجابة
-
يبلغ طول الفناء 12 قدمًا والعرض 15 قدمًا.
في المثال التالي، سنستخدم نظرية فيثاغورس\((a^2+b^2=c^2)\). توضح هذه الصيغة العلاقة بين الساقين والوتر في المثلث القائم.
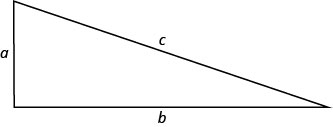
سنستخدم هذه الصيغة في المثال التالي.
شراع القارب على شكل مثلث قائم كما هو موضح. سيكون طول الوتر 17 قدمًا. سيكون طول أحد الجانبين أقل بـ 7 أقدام من طول الجانب الآخر. أوجد أطوال أضلاع الشراع.
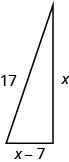
- إجابة
-
الخطوة 1. اقرأ المشكلة الخطوة 2. حدد ما تبحث عنه. نحن نبحث عن أطوال
جوانب الشراع.الخطوة 3. قم بتسمية ما تبحث عنه.
أحد الجانبين أقل بـ 7 من الآخر.دعونا\(x=\text{ length of a side of the sail}\).
\(x−7=\text{ length of other side}\)الخطوة 4. ترجم إلى معادلة. نظرًا لأن هذا مثلث
قائم، يمكننا استخدام نظرية فيثاغورس.\(a^2+b^2=c^2\) استبدل في المتغيرات. \(x^2+(x−7)^2=17^2\) الخطوة 5. حل المعادلة قم
بالتبسيط.\(x^2+x^2−14x+49=289\) \(2x^2−14x+49=289\) إنها معادلة تربيعية، لذا احصل على صفر على أحد الجانبين. \(2x^2−14x−240=0\) العامل هو العامل المشترك الأكبر. \(2(x^2−7x−120)=0\) عامل ثلاثي الحدود. \(2(x−15)(x+8)=0\) استخدم خاصية المنتج الصفري. \(2\neq 0\quad x−15=0\quad x+8=0\) حل. \(2\neq 0\quad x=15\quad x=−8\) نظرًا\(x\) لأنه جانب من المثلث،\(x=−8\) فلا
معنى له.\(2\neq 0\quad x=15\quad \cancel{x=−8}\) أوجد طول الضلع الآخر. إذا كان طول أحد
الضلعين يساوي طول الضلع الآخر


8 هو طول الجانب الآخر.الخطوة 6. تحقق من الإجابة في المشكلة
هل هذه الأرقام منطقية؟
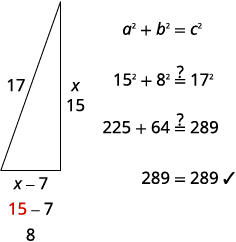
الخطوة 7. أجب على السؤال جوانب الشراع هي 8 و 15 و 17 قدمًا.
تريد جوستين وضع سطح السفينة في زاوية الفناء الخلفي لها على شكل مثلث قائم. يبلغ طول أحد جانبي سطح السفينة 7 أقدام أكثر من الجانب الآخر. الوتر هو 13. أوجد أطوال جانبي سطح السفينة.
- إجابة
-
5 أقدام و 12 قدمًا
تقع حديقة التأمل على شكل مثلث قائم، بساق واحدة يبلغ 7 أقدام. يزيد طول الوتر بمقدار واحد عن طول الساق الأخرى. أوجد طول الوتر والساق الأخرى.
- إجابة
-
24 قدمًا و 25 قدمًا
يستخدم المثال التالي الوظيفة التي تعطي ارتفاع الكائن كدالة للوقت عند رميه من 80 قدمًا فوق سطح الأرض.
سيقوم دينيس برمي كرة الشريط المطاطي لأعلى من أعلى مبنى بالحرم الجامعي. عندما يرمي الكرة\(h(t)=−16t^2+64t+80\) ذات الشريط المطاطي من ارتفاع 80 قدمًا فوق سطح الأرض\(h\)، فإن الدالة تمثل ارتفاع الكرة فوق الأرض كدالة للوقت\(t\). ابحث عن:
ⓐ أصفار هذه الدالة التي تخبرنا عندما تصطدم الكرة بالأرض
ⓑ متى ستكون الكرة فوق سطح الأرض بمقدار 80 قدمًا
ⓒ ارتفاع الكرة\(t=2\) بالثواني.
- إجابة
-
ⓐ تم العثور على أصفار هذه الدالة عن طريق الحل\(h(t)=0\). سيخبرنا هذا متى ستصل الكرة إلى الأرض.
\(\begin{array} {ll} &h(t)=0 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=0 \\ \text{Factor the GCF, }−16. &−16(t^2−4t−5)=0 \\ \text{Factor the trinomial.} &−16(t−5)(t+1)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.} \end{array} &\begin{array} {ll} t−5=0 &t+1=0 \\ t=5 &t=−1 \end{array} \end{array} \)\(t=5\)تخبرنا النتيجة أن الكرة ستصطدم بالأرض بعد 5 ثوانٍ من رميها. نظرًا لأن الوقت لا يمكن أن يكون سلبيًا،\(t=−1\) يتم تجاهل النتيجة.
ⓑ ستكون الكرة فوق سطح الأرض بمقدار 80 قدمًا عندما\(h(t)=80\).
\(\begin{array} {ll} &h(t)=80 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=80 \\ \text{Subtract 80 from both sides.} &−16t^2+64t=0 \\ \text{Factor the GCF, }−16t. &−16t(t−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.}\end{array} &\begin{array} {ll} −16t=0 &t−4=0 \\ t=0 &t=4 \end{array} \\ &\text{The ball will be at 80 feet the moment Dennis} \\ &\text{tosses the ball and then 4 seconds later, when} \\ &\text{the ball is falling.} \end{array} \)ⓒ للعثور على ارتفاع الكرة في\(t=2\) ثوانٍ نجدها\(h(2)\).
\(\begin{array} {ll} &h(t)=−16t^2+64t+80 \\ \text{To find }h(2)\text{ substitute }2\text{ for }t. &h(2)=−16(2)^2+64·2+80 \\ \text{Simplify.} &h(2)=144 \\ &\text{After 2 seconds, the ball will be at 144 feet.} \end{array}\)
ستقوم جينيفيف برمي صخرة من أعلى ممر يطل على المحيط. عندما تقوم برمي الصخرة صعودًا من ارتفاع 160 قدمًا فوق المحيط\(h\)، تمثل الدالة\(h(t)=−16t^2+48t+160\) ارتفاع الصخرة فوق المحيط كدالة للوقت\(t\). ابحث عن:
ⓐ أصفار هذه الدالة التي تخبرنا متى ستصطدم الصخرة بالمحيط
ⓑ عندما تكون الصخرة على ارتفاع 160 قدمًا فوق المحيط.
ⓒ ارتفاع الصخرة\(t=1.5\) بالثواني.
- إجابة
-
ⓐ 5 ⓑ 0؛ 3 ⓒ 196
سيلقي كاليب بنسه المحظوظ من شرفته على متن سفينة سياحية. عندما يرمي الفلس إلى أعلى من ارتفاع ١٢٨ قدمًا فوق سطح الأرض\(h\)، تُمثل الدالة\(h(t)=−16t^2+32t+128\) ارتفاع الفلس الواحد فوق المحيط كدالة للوقت\(t\). ابحث عن:
ⓐ أصفار هذه الدالة وهي عندما يصطدم الفلس بالمحيط
ⓑ عندما يكون القرش على ارتفاع 128 قدمًا فوق المحيط.
ⓒ سيكون ارتفاع البنس\(t=1\) بالثواني وهو الوقت الذي سيكون فيه البنس في أعلى نقطة له.
- إجابة
-
ⓐ 4 ⓑ 0؛ 2 ⓒ 144
قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة باستخدام المعادلات التربيعية.
المفاهيم الرئيسية
- معادلة كثيرة الحدود: معادلة كثيرة الحدود هي معادلة تحتوي على تعبير متعدد الحدود. درجة المعادلة كثيرة الحدود هي درجة كثيرة الحدود.
- المعادلة التربيعية: معادلة الشكل\(ax^2+bx+c=0\) تسمى المعادلة التربيعية.
\[a,b,c\text{ are real numbers and } a\neq 0\nonumber\]
- خاصية المنتج الصفري: إذا كان\(a·b=0\) الأمر\(a=0\) كذلك\(b=0\) أو كلاهما.
- كيفية استخدام خاصية Zero Product
- اضبط كل عامل مساويًا للصفر.
- حل المعادلات الخطية.
- تحقق.
- كيفية حل المعادلة التربيعية عن طريق التحليل.
- اكتب المعادلة التربيعية في الصورة القياسية،\(ax^2+bx+c=0\).
- عامِل التعبير التربيعي.
- استخدم خاصية المنتج الصفري.
- حل المعادلات الخطية.
- تحقق. استبدل كل حل على حدة في المعادلة الأصلية.
- صفر الدالة: بالنسبة لأي دالة\(f\)\(f(x)=0\)، إذا كانت\(x\) تساوي صفرًا للدالة.
- كيفية استخدام استراتيجية حل المشكلات لحل مشاكل الكلمات.
- اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
- حدد ما نبحث عنه.
- اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
- ترجم إلى معادلة. قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة الإنجليزية إلى معادلة جبرية.
- حل المعادلة باستخدام تقنيات الجبر المناسبة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.


