6.3: العوامل الثلاثية

Last updated
Save as PDF

Page ID: 201520

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

عامل الحدود الثلاثية للنموذج$x^2+bx+c$
العوامل الثلاثية للنموذج$ax^2+bx+c$ باستخدام التجربة والخطأ
معاملات ثلاثية الحدود للنموذج$ax^2+bx+c$ باستخدام الطريقة$ac$ ''
عامل باستخدام الاستبدال

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

ابحث عن جميع عوامل 72.
إذا فاتتك هذه المشكلة، راجع [link].
ابحث عن المنتج:$(3y+4)(2y+5)$.
إذا فاتتك هذه المشكلة، راجع [link].
قم بالتبسيط:$−9(6);\space −9(−6)$.
إذا فاتتك هذه المشكلة، راجع [link].

العوامل: القيم الثلاثية للنموذج$x^2+bx+c$

لقد تعلمت بالفعل كيفية ضرب المعادلات ذات الحدين باستخدام FOIL. ستحتاج الآن إلى «التراجع» عن عملية الضرب هذه. إن أخذ العوامل الثلاثية في الاعتبار يعني البدء بالمنتج والانتهاء بالعوامل.

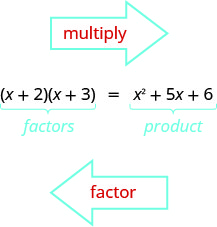
$يوضح الشكل معادلة الأقواس المفتوحة x زائد 2 أقواس مغلقة أقواس مفتوحة x زائد 3 أقواس قريبة تساوي x مربعة زائد 5 x زائد 6. يُطلق على الجانب الأيسر من المعادلة اسم العوامل بينما يُطلق على الجانب الأيمن اسم المنتج. يُطلق على السهم الذي يشير إلى اليمين اسم الضرب. يسمى السهم الذي يشير إلى اليسار بالعامل.$

لمعرفة كيفية احتساب ثلاثة حدود للشكل$x^2+bx+c$، مثل$x^2+5x+6$ وضعه في الاعتبار$(x+2)(x+3)$، دعنا نبدأ بعمليتين عامتين من الحدين للنموذج$(x+m)$ و$(x+n)$.

	$(x+m)(x+n)$
قم بالرقائق للعثور على المنتج.	$x^{2}+m x+n x+m n$
ضع في اعتبارك GCF من المصطلحات المتوسطة.	$x^{2}+(m+n) x+m n$
الحد الثلاثي الخاص بنا هو الشكل$x^2+bx+c$.	$\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}$

ويخبرنا هذا أنه لتحليل ثلاثية الحدود للنموذج$x^2+bx+c$، نحتاج إلى عاملين$(x+m)$$(x+n)$ حيث يتم$n$ ضرب$m$ الرقمين$c$ والإضافة إليهما$b$.

مثال$\PageIndex{1}$: How to Factor a Trinomial of the form $x^2+bx+c$

عامل:$x^2+11x+24$.

إجابة: $الخطوة الأولى هي كتابة معاملات x squared زائد 11x زائد 24 كحدين بالحدين الأولين x. اكتب مجموعتين من الأقواس ثم ضع x كحد أول.$ $الخطوة 2 هي إيجاد عددين m و n يضربان في c، m في n هو c ويضيفان إلى b، m زائد n هو b، لذا ابحث عن عددين يضربان في 24 ويضاعفان إلى 11. عوامل 24 هي 1 و 24 و 2 و 12 و 3 و 8 و 4 و 6. مجموع العوامل: 1 زائد 24 هو 25، 2 زائد 12 هو 14، 3 زائد 8 هو 11 و 4 زائد 6 هو 10.$ $الخطوة 3 هي استخدام m و n، في هذه الحالة، 3 و 8، كمصطلحات أخيرة للحدين. لذلك نحصل على أقواس مفتوحة x بالإضافة إلى 3 أقواس مغلقة أقواس مفتوحة x بالإضافة إلى 8 أقواس قريبة$ $الخطوة 4 هي التحقق بضرب العوامل للحصول على متعدد الحدود الأصلي.$

مثال$\PageIndex{2}$

عامل:$q^2+10q+24$.

إجابة: $(q+4)(q+6)$

مثال$\PageIndex{3}$

عامل:$t^2+14t+24$.

إجابة: $(t+2)(t+12)$

دعونا نلخص الخطوات التي استخدمناها للعثور على العوامل.

اكتب العوامل في صورة ذات حدين باستخدام الحدود الأولى x. $\quad \begin{array} {l} x^2+bx+c \\ (x\quad)(x\quad) \end{array} $
ابحث عن رقمين$m$$n$ وهذا
- اضرب إلى$c$،$m·n=c$
- أضف إلى$b$،$m+n=b$
استخدم$m$$n$ وكالمصطلحات الأخيرة للعوامل. $\quad (x+m)(x+n)$
تحقق من ذلك بضرب العوامل.

في المثال الأول، كانت جميع المصطلحات في الثلاثية إيجابية. ماذا يحدث عندما تكون هناك مصطلحات سلبية؟ حسنًا، يعتمد ذلك على المصطلح السلبي. دعونا ننظر أولاً إلى القيم الثلاثية ذات المدى المتوسط السلبية فقط.

كيف تحصل على منتج إيجابي ومبلغ سلبي؟ نحن نستخدم رقمين سالبين.

مثال$\PageIndex{4}$

عامل:$y^2−11y+28$.

إجابة

مرة أخرى، مع المدى الأخير الإيجابي$28$، والأجل المتوسط السلبي$−11y$، نحتاج إلى عاملين سلبيين. ابحث عن رقمين يتم ضربهما$28$ والإضافة إليهما$−11$.
$\begin{array} {ll} &y^2−11y+28 \\ \text{Write the factors as two binomials with first terms }y. &( y \quad )( y \quad ) \\ \text{Find two numbers that: multiply to }28\text{ and add to }−11.\end{array}$

عوامل$28$	مجموع العوامل
\ (28\)» data-valign= «top>»$−1,\space −28$ $−2,\space −14$ $−4,\space −7$	$−1+(−28)=−29$ $−2+(−14)=−16$ $−4+(−7)=−11^∗$

$\begin{array} {ll} \text{Use }−4,\space −7\text{ as the last terms of the binomials.} &(y−4)(y−7) \\ \text{Check:} & \\ \hspace{30mm} (y−4)(y−7) & \\ \hspace{25mm} y^2−7y−4y+28 & \\ \hspace{30mm} y^2−11y+28\checkmark & \end{array} $

مثال$\PageIndex{5}$

عامل:$u^2−9u+18$.

إجابة: $(u−3)(u−6)$

مثال$\PageIndex{6}$

عامل:$y^2−16y+63$.

إجابة: $(y−7)(y−9)$

الآن، ماذا لو كان الحد الأخير في الثلاثية سالبًا؟ فكر في FOIL. المصطلح الأخير هو نتاج المصطلحات الأخيرة في الحدين. ينتج المنتج السالب عن ضرب رقمين بإشارات معاكسة. يجب أن تكون حريصًا جدًا على اختيار العوامل للتأكد من حصولك على العلامة الصحيحة للمدى المتوسط أيضًا.

كيف تحصل على منتج سلبي ومبلغ إيجابي؟ نحن نستخدم رقمًا موجبًا واحدًا ورقمًا سالبًا.

عند حساب القيم الثلاثية، يجب أن تكون المصطلحات مكتوبة بترتيب تنازلي - بالترتيب من أعلى درجة إلى أدنى درجة.

مثال$\PageIndex{7}$

عامل:$2x+x^2−48$.

إجابة

$\begin{array} {ll} &2x+x^2−48 \\ \text{First we put the terms in decreasing degree order.} &x^2+2x−48 \\ \text{Factors will be two binomials with first terms }x. &(x\quad)(x\quad) \end{array} $

عوامل −48-48	مجموع العوامل
$−1,\space 48$ $−2,\space 24$ $−3,\space 16$ $−4,\space 12$ $−6,\space 8$	$−1+48=47$ $−2+24=22$ $−3+16=13$ $−4+12=8$ $−6+8=2^∗$

$\begin{array} {ll} \text{Use }−6,\space 8\text{ as the last terms of the binomials.} &(x−6)(x+8) \\ \text{Check:} & \\ \hspace{30mm} (x−6)(x+8) & \\ \hspace{25mm} x^2−6q+8q−48 & \\ \hspace{30mm} x^2+2x−48\checkmark & \end{array} $

مثال$\PageIndex{8}$

عامل:$9m+m^2+18$.

إجابة: $(m+3)(m+6)$

مثال$\PageIndex{9}$

عامل:$−7n+12+n^2$.

إجابة: $(n−3)(n−4)$

ستحتاج أحيانًا إلى تحليل القيم الثلاثية للنموذج$x^2+bxy+cy^2$ باستخدام متغيرين، مثل$x^2+12xy+36y^2$. المصطلح الأول$x^2$، هو نتاج المصطلحات الأولى للعوامل ذات الحدين،$x·x$. يعني المصطلح الأخير أن المصطلحات الثانية من العوامل ذات الحدين يجب أن تحتوي كل منها$y$.$y^2$ للحصول على المعاملات$b$$c$، يمكنك استخدام نفس العملية الملخصة في How To Factor trymals الثلاثية.

مثال$\PageIndex{10}$

عامل:$r^2−8rs−9s^2$.

إجابة

نحن بحاجة$r$ في الفصل الأول من كل معادلة ذات حدين$s$ وفي الفصل الثاني. المصطلح الأخير من الثلاثي سلبي، لذلك يجب أن تحتوي العوامل على علامات معاكسة.
$\begin{array} {ll} &r^2−8rs−9s^2 \\ \text{Note that the first terms are }r,\text{last terms contain }s. &(r\quad s)(r\quad s) \\ \text{Find the numbers that multiply to }−9\text{ and add to }−8. \end{array}$

عوامل$−9$	مجموع العوامل
\ (−9\)» data-valign= «top>»$1,\space −9$	$−1+9=8$
\ (−9\)» data-valign= «top>»$−1,\space 9$	$1+(−9)=−8^∗$
\ (−9\)» data-valign= «top>»$3,\space −3$	$3+(−3)=0$

$\begin{array} {ll} \text{Use }1,\space -9\text{ as coefficients of the last terms.} &(r+s)(r−9s) \\ \text{Check:} & \\ \hspace{30mm} (r−9s)(r+s) & \\ \hspace{25mm} r^2+rs−9rs−9s^2 & \\ \hspace{30mm} r^2−8rs−9s^2\checkmark & \end{array} $

مثال$\PageIndex{11}$

عامل:$a^2−11ab+10b^2$.

إجابة: $(a−b)(a−10b)$

مثال$\PageIndex{12}$

عامل:$m^2−13mn+12n^2$.

إجابة: $(m−n)(m−12n)$

بعض العبارات الثلاثية أساسية. الطريقة الوحيدة للتأكد من ثلاثية الحدود هي الأولية هي سرد جميع الاحتمالات وإظهار أن أيًا منها لا يعمل.

مثال$\PageIndex{13}$

عامل:$u^2−9uv−12v^2$.

إجابة

نحن بحاجة$u$ في الفصل الأول من كل معادلة ذات حدين$v$ وفي الفصل الثاني. المصطلح الأخير من الثلاثي سلبي، لذلك يجب أن تحتوي العوامل على علامات معاكسة.
$\begin{array} {ll} &u^2−9uv−12v^2 \\ \text{Note that the first terms are }u,\text{ last terms contain }v. &(u\quad v)(u\quad v) \\ \text{Find the numbers that multiply to }−12\text{ and add to }−9. & \end{array} $

عوامل$−12$	مجموع العوامل
\ (−12\)» data-valign= «top>»$1,−12$ $−1,12$ $2,−6$ $−2,6$ $3,−4$ $−3,4$	$1+(−12)=−11$ $−1+12=11$ $2+(−6)=−4$ $−2+6=4$ $3+(−4)=−1$ $−3+4=1$

لاحظ أنه لا توجد أزواج عوامل تعطينا$−9$ كمجموع. الثلاثي هو الأول.

مثال$\PageIndex{14}$

عامل:$x^2−7xy−10y^2$.

إجابة: أولي

مثال$\PageIndex{15}$

عامل:$p^2+15pq+20q^2$.

إجابة: أولي

دعونا نلخص الطريقة التي طورناها للتو لحساب القيم الثلاثية للنموذج$x^2+bx+c$.

استراتيجية لتخصيم القيم الثلاثية للنموذج$x^2+bx+c$

عندما نأخذ في الاعتبار الثلاثي، ننظر إلى علامات مصطلحاته أولاً لتحديد علامات العوامل ذات الحدين.

	$ x^{2}+b x+c $
	$ (x+m)(x+n) $
عندما$ c $ تكون إيجابية،$ m $$ n $ ولها نفس العلامة.
$ b $إيجابي		$ b $سلبي
$ m,n $إيجابي		$ m,n $سلبي
$ x^{2}+5 x+6 $		$ x^{2}-6 x+8 $
$ (x+2)(x+3) $		$ (x-4)(x-2) $
نفس العلامات		نفس العلامات
عندما$ c $ تكون سلبية،$ m $$ n $ ولها علامة عكسية.
$ x^{2}+x-12 $		$ x^{2}-2 x-15 $
$ (x+4)(x-3) $		$ (x-5)(x+3) $
علامات معاكسة		علامات معاكسة

لاحظ أنه في حالة$m$ وجود علامات$n$ معاكسة، فإن علامة العلامة ذات القيمة المطلقة الأكبر تتطابق مع علامة$b$.

العوامل الثلاثية للنموذج بحد أقصى ² + مربع+c باستخدام التجربة والخطأ

تتمثل خطوتنا التالية في حساب المثلثات الثلاثية التي لا يكون معاملها الرئيسي هو 1، وهي ثلاثية الحدود للنموذج$ax^2+bx+c$.

تذكر دائمًا التحقق من GCF أولاً! في بعض الأحيان، بعد حساب GCF، يصبح المعامل الرئيسي للثلاثية الحدود$1$ ويمكنك حسابه بالطرق التي استخدمناها حتى الآن. دعونا نفعل مثالاً لنرى كيف يعمل هذا.

مثال$\PageIndex{16}$

عامل بالكامل:$4x^3+16x^2−20x$.

إجابة

$\begin{array} {lll} \text{Is there a greatest common factor?} &\qquad &4x^3+16x^2−20x \\ \quad \text{Yes, }GCF=4x.\text{ Factor it.} & &4x(x^2+4x−5) \\ & & \\ & & \\ \text{Binomial, trinomial, or more than three terms?} & & \\ \quad \text{It is a trinomial. So “undo FOIL.”} & &4x(x\quad)(x\quad) \\ & & \\ & & \\ \text{Use a table like the one shown to find two numbers that} & &4x(x−1)(x+5) \\ \text{multiply to }−5\text{ and add to }4. & & \\ & & \\ & & \end{array} $

عوامل$−5$	مجموع العوامل
\ (−5\)» data-valign= «top>»$−1,5$ $1,−5$	$−1+5=4^∗$ $1+(−5)=−4$

$\begin{array} {l} \text{Check:}\\ \hspace{27mm}4x(x−1)(x+5) \\ \hspace{25mm} 4x(x^2+5x−x−5) \\ \hspace{30mm} 4x(x^2+4x−5) \\ \hspace{25mm} 4x^3+16x2−20x\checkmark \end{array} $

مثال$\PageIndex{17}$

عامل بالكامل:$5x^3+15x^2−20x$.

إجابة: $5x(x−1)(x+4)$

مثال$\PageIndex{18}$

عامل بالكامل:$6y^3+18y^2−60y$.

إجابة: $6y(y−2)(y+5)$

ماذا يحدث عندما لا يكون المعامل الرائد$1$ موجودًا ولا يوجد GCF؟ هناك العديد من الطرق التي يمكن استخدامها لتحليل هذه القيم الثلاثية. أولاً سنستخدم طريقة التجربة والخطأ.

دعونا نأخذ في الاعتبار الثلاثي$3x^2+5x+2$.

من عملنا السابق، نتوقع أن يتحول هذا إلى حدين.

\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]

نحن نعلم أن المصطلحات الأولى للعوامل ذات الحدين ستتضاعف لتعطينا$3x^2$. العوامل الوحيدة$3x^2$ هي$1x,\space 3x$. يمكننا وضعها في الحدود الثنائية.

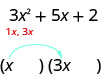
$كثير الحدود هو 3x مربع زائد 5x زائد 2. يوجد زوجان من الأقواس، حيث تكون المصطلحات الأولى فيهما x و 3x.$

تحقق من: هل$1x·3x=3x^2$؟

نحن نعلم أن المصطلحات الأخيرة من الحدين ستتضاعف إلى$2$. نظرًا لأن هذه العبارة الثلاثية تحتوي على جميع المصطلحات الإيجابية، فإننا نحتاج فقط إلى النظر في العوامل الإيجابية. العوامل الوحيدة$2$ هي$1$ و$2$. ولكن لدينا الآن حالتان يجب مراعاتهما حيث ستحدث فرقًا إذا$1$ كتبنا$2$$2$ أو$1$.

ما هي العوامل الصحيحة؟ لنقرر ذلك، نضرب المصطلحات الداخلية والخارجية.

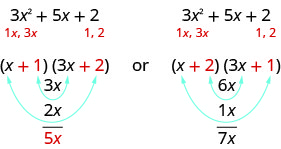
$يوضِّح الشكل رقم ٣ × مربع زائد ٥ × زائد ٢ وزوجين محتملين من العوامل. واحد هو الأقواس المفتوحة x بالإضافة إلى 1 أقواس مغلقة أقواس مفتوحة 3x بالإضافة إلى قوسين مغلقين. والآخر هو الأقواس المفتوحة x بالإضافة إلى 2 أقواس مغلقة أقواس مفتوحة 3x بالإضافة إلى 1 أقواس قريبة. في كل حالة، تظهر الأسهم وهي تقرن المصطلح الأول للعامل الأول مع الفصل الأخير من العامل الثاني والحد الأول من العامل الثاني مع الحد الأخير من العامل الأول.$

نظرًا لأن المدى المتوسط للثلاثية هو$5x$، فإن العوامل في الحالة الأولى ستنجح. دعونا نستخدم FOIL للتحقق.

\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]

نتيجة التخصيم لدينا هي:

\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]

مثال$\PageIndex{19}$: How to Factor a Trinomial Using Trial and Error

عامل يستخدم التجربة والخطأ بالكامل:$3y^2+22y+7$.

إجابة: $الخطوة 1 هي كتابة الثلاثية بترتيب تنازلي. تم ترتيب المربع الثلاثي 3 y زائد 22y زائد 7 بترتيب تنازلي بالفعل.$ $الخطوة 2 هي حساب GCF. هنا، لا يوجد أحد.$ $الخطوة 3 هي العثور على جميع أزواج عوامل الحد الأول. العوامل الوحيدة هنا هي 1y و 3y. نظرًا لوجود زوج واحد فقط، يمكننا وضع كل منهما كمصطلح أول بين قوسين.$ $الخطوة 4 هي إيجاد جميع أزواج العوامل للمصطلح الثالث. هنا، الزوج الوحيد هو 1 و 7.$ $الخطوة 5 هي اختبار جميع المجموعات الممكنة من العوامل حتى يتم العثور على المنتج الصحيح. بالنسبة للعوامل المحتملة، افتح الأقواس y زائد 1 أقواس مغلقة أقواس مفتوحة 37 زائد 7 أقواس قريبة، المنتج هو 3 y مربع زائد 10 سنوات زائد 7. بالنسبة للعوامل المحتملة، افتح الأقواس y بالإضافة إلى 7 أقواس مغلقة أقواس مفتوحة 3y بالإضافة إلى 1 أقواس قريبة، يكون المنتج هو 3 y squared بالإضافة إلى 22y زائد 7، وهو المنتج الصحيح. وبالتالي، فإن العوامل الصحيحة هي الأقواس المفتوحة y بالإضافة إلى 7 أقواس مغلقة أقواس مفتوحة 3y بالإضافة إلى 1 أقواس قريبة.$ $الخطوة 6 هي التحقق عن طريق الضرب.$

مثال$\PageIndex{20}$

عامل يستخدم التجربة والخطأ بالكامل:$2a^2+5a+3$.

إجابة: $(a+1)(2a+3)$

مثال$\PageIndex{21}$

عامل يستخدم التجربة والخطأ بالكامل:$4b^2+5b+1$.

إجابة: $(b+1)(4b+1)$

عامل الحدود الثلاثية للنموذج$ax^2+bx+c$ USING TRIAL AND ERROR.

اكتب الثلاثية بترتيب تنازلي للدرجات حسب الحاجة.
عامل أي GCF.
أوجد جميع أزواج عوامل الحد الأول.
أوجد جميع أزواج عوامل الحد الثالث.
اختبر جميع المجموعات الممكنة من العوامل حتى يتم العثور على المنتج الصحيح.
تحقق عن طريق الضرب.

تذكر أنه عندما يكون الحد المتوسط سالبًا ويكون المصطلح الأخير إيجابيًا، يجب أن تكون العلامات في الحدين سالبة.

مثال$\PageIndex{22}$

عامل يستخدم التجربة والخطأ بالكامل:$6b^2−13b+5$.

إجابة

تم ترتيب الثلاثي بالفعل ترتيبًا تنازليًا.	$.$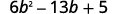
ابحث عن عوامل الفصل الدراسي الأول.	$.$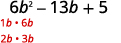
ابحث عن عوامل الفصل الأخير. ضع في اعتبارك العلامات. نظرًا لأن المصطلح الأخير إيجابي$5$، يجب أن تكون عوامله إيجابية أو كلاهما سلبية. معامل المدى المتوسط سلبي، لذلك نستخدم العوامل السلبية.	$.$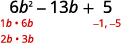

ضع في اعتبارك جميع مجموعات العوامل.

$6b^2−13b+5$
العوامل المحتملة	المنتج
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>$(b−1)(6b−5)$	\ (6b^2−13b+5\) المنتج» data-valign= top>$6b^2−11b+5$
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>$(b−5)(6b−1)$	\ (6b^2−13b+5\) المنتج» data-valign= top>$6b^2−31b+5$
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>$(2b−1)(3b−5)$	\ (6b^2−13b+5\) المنتج» data-valign= = middle>$6b^2−13b+5^∗$
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>$(2b−5)(3b−1)$	\ (6b^2−13b+5\) المنتج» data-valign= = middle>$6b^2−17b+5$

$\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} $

مثال$\PageIndex{23}$

عامل يستخدم التجربة والخطأ بالكامل:$8x^2−14x+3$.

إجابة: $(2x−3)(4x−1)$

مثال$\PageIndex{24}$

عامل يستخدم التجربة والخطأ بالكامل:$10y^2−37y+7$.

إجابة: $(2y−7)(5y−1)$

عندما نضع تعبيرًا في الاعتبار، فإننا نبحث دائمًا عن العامل المشترك الأكبر أولاً. إذا لم يكن للتعبير عامل مشترك أكبر، فلا يمكن أن يكون هناك عامل واحد في عوامله أيضًا. قد يساعدنا هذا في التخلص من بعض تركيبات العوامل المحتملة.

مثال$\PageIndex{25}$

عامل يستخدم التجربة والخطأ بالكامل:$18x^2−37xy+15y^2$.

إجابة

تم ترتيب الثلاثي بالفعل ترتيبًا تنازليًا.	$.$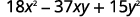
ابحث عن عوامل الفصل الدراسي الأول.	$.$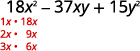
ابحث عن عوامل الفصل الأخير. ضع في اعتبارك العلامات. نظرًا لأن 15 إيجابي ومعامل المدى المتوسط سلبي، فإننا نستخدم العوامل السلبية.	$.$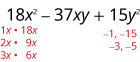

فكر في جميع مجموعات العوامل.

$يوضِّح هذا الجدول العوامل المحتملة والنواتج المناظرة للمربع الثلاثي 18 x ناقص 37xy زائد 15 y مربعًا. في بعض أزواج العوامل، عندما يحتوي أحد العوامل على مصطلحين مع عامل مشترك، يتم تمييز هذا العامل. في مثل هذه الحالات، لا يعد المنتج خيارًا لأنه إذا لم يكن للثلاثي أي عوامل مشتركة، فلا يمكن أن يحتوي أي عامل على عامل مشترك. العامل: الأقواس المفتوحة x ناقص 1y أقواس الإغلاق الأقواس المفتوحة 18x ناقص 15y أقواس الإغلاق، مظللة. العامل، الأقواس المفتوحة x ناقص 15y أقواس الإغلاق الأقواس المفتوحة 18x ناقص 1y أقواس الإغلاق؛ المنتج: 18 × مربع ناقص 271xy بالإضافة إلى 15 y مربعًا. عامل الأقواس المفتوحة x ناقص 3y أقواس الإغلاق الأقواس المفتوحة 18x ناقص 5 y أقواس الإغلاق؛ المنتج: 18 × مربع ناقص 59xy بالإضافة إلى 15 y مربعًا. العامل: الأقواس المفتوحة x ناقص 5y أقواس الإغلاق الأقواس المفتوحة 18x ناقص 3y تم تمييز أقواس الإغلاق. العامل: الأقواس المفتوحة 2x ناقص 1y أقواس الإغلاق الأقواس المفتوحة 9x ناقص 15y تم تمييز أقواس الإغلاق. العامل: الأقواس المفتوحة 2x ناقص 15y أقواس الإغلاق الأقواس المفتوحة 9x ناقص 1y أقواس الإغلاق؛ المنتج 18 × مربع ناقص 137 xy بالإضافة إلى 15 سنة مربعة. العامل: الأقواس المفتوحة 2x ناقص 3y أقواس الإغلاق الأقواس المفتوحة 9x ناقص 5y أقواس الإغلاق؛ المنتج: 18 × مربع ناقص 37xy زائد 15 y مربعًا، وهو الثلاثي الأصلي. العامل: الأقواس المفتوحة 2x ناقص 57 أقواس الإغلاق الأقواس المفتوحة 9x ناقص 3y تم تمييز أقواس الإغلاق. العامل: الأقواس المفتوحة 3x ناقص 1y أقواس الإغلاق الأقواس المفتوحة 6x ناقص 15y تم تمييز أقواس الإغلاق. العامل: الأقواس المفتوحة 3x ناقص 15y أقواس الإغلاق المميزة الأقواس المفتوحة 6x ناقص 1y أقواس الإغلاق. العامل: الأقواس المفتوحة 3x ناقص 3y أقواس الإغلاق المميزة الأقواس المفتوحة 6x ناقص 5y.$

$\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} $

مثال$\PageIndex{26}$

عامل يستخدم التجربة والخطأ بالكامل$18x^2−3xy−10y^2$.

إجابة: $(3x+2y)(6x−5y)$

مثال$\PageIndex{27}$

عامل يستخدم التجربة والخطأ بالكامل:$30x^2−53xy−21y^2$.

إجابة: $(3x+y)(10x−21y)$

لا تنس البحث عن GCF أولاً وتذكر ما إذا كان المعامل الرئيسي سالبًا، وكذلك GCF.

مثال$\PageIndex{28}$

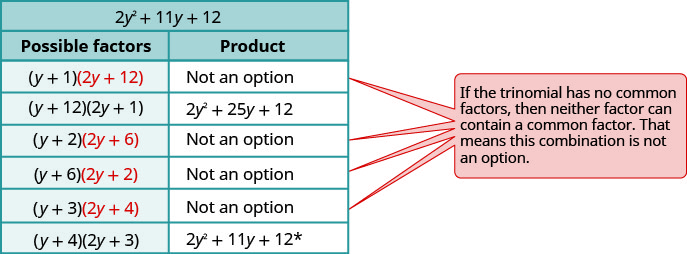
عامل يستخدم التجربة والخطأ بالكامل:$−10y^4−55y^3−60y^2$.

إجابة

	$.$
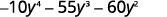
لاحظ العامل المشترك الأكبر، لذا ضعه في الاعتبار أولاً.	$.$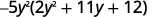
عامل ثلاثي الحدود.	$.$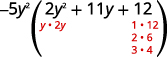

ضع في اعتبارك جميع المجموعات.

$يوضِّح هذا الجدول العوامل المحتملة ومنتج المربع الثلاثي الذي يساوي ٢ ص زائد ١١ سنة زائد ١٢. في بعض أزواج العوامل، عندما يحتوي أحد العوامل على مصطلحين مع عامل مشترك، يتم تمييز هذا العامل. في مثل هذه الحالات، لا يعد المنتج خيارًا لأنه إذا لم يكن للثلاثي أي عوامل مشتركة، فلا يمكن أن يحتوي أي عامل على عامل مشترك. العامل: تم تمييز y plus 1 و 2y plus 12. العامل: y plus 12، 2y plus 1؛ المنتج: 2 سنة مربعة زائد 25 سنة زائد 12. العامل: تم تمييز y plus 2 و 2y plus 6. العامل: تم تمييز y plus 6 و 2y plus 2. العامل: تم تمييز y plus 3 و 2y plus 4. العامل: y plus 4، 2y plus 3؛ المنتج: 2 ص مربع زائد 11 سنة زائد 12. هذه هي النسخة الثلاثية الأصلية.$

$\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} $

مثال$\PageIndex{29}$

عامل يستخدم التجربة والخطأ بالكامل:$15n^3−85n^2+100n$.

إجابة: $5n(n−4)(3n−5)$

مثال$\PageIndex{30}$

عامل يستخدم التجربة والخطأ بالكامل:$56q^3+320q^2−96q$.

إجابة: $8q(q+6)(7q−2)$

معاملات ثلاثية الحدود للنموذج$ax^2+bx+c$ باستخدام الطريقة «$ac$»

هناك طريقة أخرى لحساب القيم الثلاثية للنموذج$ax^2+bx+c$ وهي طريقة «$ac$». (تسمى الطريقة «$ac$» أحيانًا طريقة التجميع.) تعد الطريقة «$ac$» في الواقع امتدادًا للطرق التي استخدمتها في القسم الأخير لحساب التثليث بالمعامل الرائد الأول. هذه الطريقة منظمة للغاية (خطوة بخطوة)، وهي تعمل دائمًا!

مثال$\PageIndex{31}$: How to Factor Trinomials using the “ac” Method

عامل باستخدام طريقة «$ac$»:$6x^2+7x+2$.

إجابة: $الخطوة 1 هي حساب GCF. لا يوجد شيء في 6 × مربع زائد 7x plus 2.$ $الخطوة 2 هي العثور على منتج a و c. منتج 6 و 2 هو 12.$ $الخطوة 3 هي إيجاد عددين m و n بحيث يكون mn هو ac و m زائد n هو b، لذلك نحتاج إلى الأرقام التي تضرب إلى 12 وتضاف إلى 7. يجب أن يكون كلا العاملين إيجابيين. 3 مرات 4 هي 12 و 3 زائد 4 هي 7.$ $الخطوة 4 هي تقسيم الحد الأوسط باستخدام m و n. لذلك نعيد كتابة 7 x كـ 3x بالإضافة إلى 4x. ستعطي نفس النتيجة إذا استخدمنا 4x plus 3x. عند إعادة الكتابة، نحصل على 6 × مربع زائد 3x بالإضافة إلى 4x زائد 2. لاحظ أن هذا هو نفس متعدد الحدود الأصلي. قمنا فقط بتقسيم المدى المتوسط للحصول على نموذج أكثر فائدة$ $الخطوة 5 هي الأخذ في الاعتبار عن طريق التجميع. لذلك، نحصل على 3 × أقواس مفتوحة 2x بالإضافة إلى 1 أقواس مغلقة بالإضافة إلى قوسين مفتوحين 2x بالإضافة إلى 1 أقواس قريبة. هذا يساوي 2x زائد 1، 3x زائد 2.$ $الخطوة 6 هي التحقق بضرب العوامل.$

مثال$\PageIndex{32}$

عامل باستخدام طريقة «$ac$»:$6x^2+13x+2$.

إجابة: $(x+2)(6x+1)$

مثال$\PageIndex{33}$

عامل باستخدام طريقة «$ac$»:$4y^2+8y+3$.

إجابة: $(2y+1)(2y+3)$

يتم تلخيص الطريقة «$ac$» هنا.

عامل الحدود الثلاثية للنموذج$ax^2+bx+c$ USING THE “$ac$” METHOD.

عامل أي GCF.
ابحث عن المنتج$ac$.
ابحث عن رقمين$m$$n$ وهذا:
$\begin{array} {ll} \text{Multiply to }ac &m·n=a·c \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} $
قسّم المدى المتوسط باستخدام$m$ و$n$. $ax^2+mx+nx+c$
عامل حسب التجميع.
تحقق من ذلك بضرب العوامل.

لا تنس البحث عن عامل مشترك!

مثال$\PageIndex{34}$

عامل باستخدام طريقة «$ac$»:$10y^2−55y+70$.

إجابة

هل هناك عامل مشترك أكبر؟
نعم. GCF هو$5$.		$.$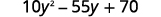
ضع في اعتبارك ذلك.		$.$
يحتوي الثلاثي الموجود داخل الأقواس على معامل رئيسي ليس كذلك$1$.		$.$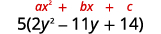
ابحث عن المنتج$ac$.	$ac=28$
ابحث عن رقمين يتم ضربهما في$ac$	$(−4)(−7)=28$
وأضف إلى$b$.	$−4(−7)=−11$
قسّم المدى المتوسط.		$.$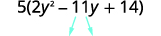
		$.$
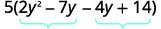
ضع في الاعتبار الثلاثي عن طريق التجميع.		$.$
		$.$
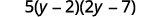
تحقق من ذلك بضرب جميع العوامل الثلاثة. $\hspace{50mm} 5(y−2)(2y−7)$ $\hspace{45mm} 5(2y^2−7y−4y+14)$ $\hspace{48mm} 5(2y^2−11y+14)$ $\hspace{49mm} 10y^2−55y+70\checkmark$

مثال$\PageIndex{35}$

عامل باستخدام طريقة «$ac$»:$16x^2−32x+12$.

إجابة: $4(2x−3)(2x−1)$

مثال$\PageIndex{36}$

عامل باستخدام طريقة «$ac$»:$18w^2−39w+18$.

إجابة: $3(3w−2)(2w−3)$

عامل باستخدام الاستبدال

في بعض الأحيان لا يبدو أن ثلاثية الحدود في$ax^2+bx+c$ الشكل. ومع ذلك، يمكننا في كثير من الأحيان إجراء استبدال مدروس يسمح لنا بجعله مناسبًا$ax^2+bx+c$ للنموذج. وهذا ما يسمى التخصيم عن طريق الاستبدال. إنه معيار$u$ للاستخدام في الاستبدال.

في$ax^2+bx+c$، يحتوي الحد الأوسط على متغير$x$، ومربعه$x^2$ هو الجزء المتغير من الحد الأول. ابحث عن هذه العلاقة أثناء محاولتك العثور على بديل.

مثال$\PageIndex{37}$

عامل عن طريق الاستبدال:$x^4−4x^2−5$.

إجابة

الجزء المتغير من الحد الأوسط هو$x^2$ ومربعه،$x^4$، هو الجزء المتغير من المصطلح الأول. (نحن نعلم$(x^2)^2=x^4)$. إذا سمحنا بذلك$u=x^2$، يمكننا وضع المعادلة الثلاثية$ax^2+bx+c$ بالشكل الذي نحتاجه لأخذها في الاعتبار.

	$x^4−4x^2−5$
أعد كتابة الثلاثية للتحضير للاستبدال.	$(x^2)^2−4(x^2)-5$
دع$u=x^2$ واستبدل.	$(u)^2−4(u)-5$
عامل ثلاثي الحدود.	$(u+1)(u-5)$
استبدل$u$ بـ$x^2$.	$(x^2+1)(x^2-5)$
تحقق من: $\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}$

مثال$\PageIndex{38}$

عامل عن طريق الاستبدال:$h^4+4h^2−12$.

إجابة: $(h^2−2)(h^2+6)$

مثال$\PageIndex{39}$

عامل عن طريق الاستبدال:$y^4−y^2−20$.

إجابة: $(y^2+4)(y^2−5)$

في بعض الأحيان لا يكون التعبير الذي سيتم استبداله أحادي الحد.

مثال$\PageIndex{40}$

عامل عن طريق الاستبدال:$(x−2)^2+7(x−2)+12$

إجابة

يتم تربيع المعادلة ذات الحدين في المدى المتوسط في الفصل الدراسي الأول.$(x−2)$ إذا سمحنا$u=x−2$ واستبدلنا، ستكون معادلتنا الثلاثية في$ax^2+bx+c$ الشكل.

	$.$
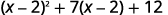
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$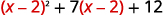
دع$u=x−2$ واستبدل.	$.$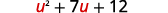
عامل ثلاثي الحدود.	$.$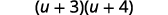
استبدل$u$ بـ$x−2$.	$.$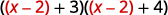
قم بالتبسيط داخل الأقواس.	$.$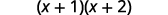

يمكن أيضًا أخذ ذلك في الاعتبار عن طريق ضرب المصطلحات المتشابهة$(x−2)^2$ أولاً$7(x−2)$ ثم الجمع بين المصطلحات المتشابهة ثم العوملة. يفضل معظم الطلاب طريقة الاستبدال.

مثال$\PageIndex{41}$

عامل عن طريق الاستبدال:$(x−5)^2+6(x−5)+8$.

إجابة: $(x−3)(x−1)$

مثال$\PageIndex{42}$

عامل عن طريق الاستبدال:$(y−4)^2+8(y−4)+15$.

إجابة: $(y−1)(y+1)$

شاهد هذا الفيديو للحصول على تعليمات إضافية وممارسة مع التخصيم.

المفاهيم الرئيسية

كيفية حساب القيم الثلاثية للنموذج$x^2+bx+c$.
1. اكتب العوامل في صورة ذات حدين باستخدام الحدود الأولى x. $\quad \begin{array} (l) x^2+bx+c \\ (x\quad)(x\quad)\end{array}$
2. ابحث عن رقمين$m$$n$ وهذا
  $\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}$
3. استخدم$m$$n$ وكالمصطلحات الأخيرة للعوامل. $\qquad (x+m)(x+n)$
4. تحقق من ذلك بضرب العوامل.
إستراتيجية احتساب القيم الثلاثية للنموذج$x^2+bx+c$: عندما نضع المعادلة الثلاثية في الاعتبار، ننظر إلى علامات شروطها أولاً لتحديد علامات العوامل ذات الحدين.

بالنسبة للأشكال الثلاثية للنموذج:$x^2+bx+c = (x+m)(x+n)$

عندما$c$ تكون إيجابية،$m$$n$ ويجب أن تحمل نفس العلامة (وستكون هذه علامة$b$ ).

أمثلة:$x^2+5x+6=(x+2)(x+3)$،$x^2−6x+8 = (x−4)(x−2)$

عندما$c$ تكون سلبية،$m$$n$ ولها علامات معاكسة. الأكبر من$m$ $n$وسيحمل علامة$b$.

أمثلة:$x^2+x−12=(x+4)(x−3)$$x^2−2x−15=(x−5)(x+3)$

لاحظ أنه في حالة$m$ وجود علامات$n$ معاكسة، فإن علامة العلامة ذات القيمة المطلقة الأكبر تتطابق مع علامة$b$.
كيفية حساب القيم الثلاثية للنموذج$ax^2+bx+c$ باستخدام التجربة والخطأ.
1. اكتب الثلاثية بترتيب تنازلي للدرجات حسب الحاجة.
2. عامل أي GCF.
3. أوجد جميع أزواج عوامل الحد الأول.
4. أوجد جميع أزواج عوامل الحد الثالث.
5. اختبر جميع المجموعات الممكنة من العوامل حتى يتم العثور على المنتج الصحيح.
6. تحقق عن طريق الضرب.
كيفية حساب القيم الثلاثية للنموذج$ax^2+bx+c$ باستخدام الطريقة «$ac$».
1. عامل أي GCF.
2. ابحث عن المنتج$ac$.
3. ابحث عن رقمين$m$$n$ وهذا:
  $\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}$
4. قسّم المدى المتوسط باستخدام$m$ و$n$. $\quad ax^2+mx+nx+c$
5. عامل حسب التجميع.
6. تحقق من ذلك بضرب العوامل.

	\((x+m)(x+n)\)
قم بالرقائق للعثور على المنتج.	\(x^{2}+m x+n x+m n\)
ضع في اعتبارك GCF من المصطلحات المتوسطة.	\(x^{2}+(m+n) x+m n\)
الحد الثلاثي الخاص بنا هو الشكل\(x^2+bx+c\).	\(\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}\)

عوامل\(−9\)	مجموع العوامل
\ (−9\)» data-valign= «top>»\(1,\space −9\)	\(−1+9=8\)
\ (−9\)» data-valign= «top>»\(−1,\space 9\)	\(1+(−9)=−8^∗\)
\ (−9\)» data-valign= «top>»\(3,\space −3\)	\(3+(−3)=0\)

	\( x^{2}+b x+c \)
	\( (x+m)(x+n) \)
عندما\( c \) تكون إيجابية،\( m \)\( n \) ولها نفس العلامة.
\( b \)إيجابي		\( b \)سلبي
\( m,n \)إيجابي		\( m,n \)سلبي
\( x^{2}+5 x+6 \)		\( x^{2}-6 x+8 \)
\( (x+2)(x+3) \)		\( (x-4)(x-2) \)
نفس العلامات		نفس العلامات
عندما\( c \) تكون سلبية،\( m \)\( n \) ولها علامة عكسية.
\( x^{2}+x-12 \)		\( x^{2}-2 x-15 \)
\( (x+4)(x-3) \)		\( (x-5)(x+3) \)
علامات معاكسة		علامات معاكسة

\(6b^2−13b+5\)
العوامل المحتملة	المنتج
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>\((b−1)(6b−5)\)	\ (6b^2−13b+5\) المنتج» data-valign= top>\(6b^2−11b+5\)
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>\((b−5)(6b−1)\)	\ (6b^2−13b+5\) المنتج» data-valign= top>\(6b^2−31b+5\)
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>\((2b−1)(3b−5)\)	\ (6b^2−13b+5\) المنتج» data-valign= = middle>\(6b^2−13b+5^∗\)
\ (6b^2−13b+5\) العوامل المحتملة» data-valign= top>\((2b−5)(3b−1)\)	\ (6b^2−13b+5\) المنتج» data-valign= = middle>\(6b^2−17b+5\)

	\(x^4−4x^2−5\)
أعد كتابة الثلاثية للتحضير للاستبدال.	\((x^2)^2−4(x^2)-5\)
دع\(u=x^2\) واستبدل.	\((u)^2−4(u)-5\)
عامل ثلاثي الحدود.	\((u+1)(u-5)\)
استبدل\(u\) بـ\(x^2\).	\((x^2+1)(x^2-5)\)
تحقق من: \(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\)

هل هناك عامل مشترك أكبر؟
نعم. GCF هو\(5\).		$.$
ضع في اعتبارك ذلك.		$.$
يحتوي الثلاثي الموجود داخل الأقواس على معامل رئيسي ليس كذلك\(1\).		$.$
ابحث عن المنتج\(ac\).	\(ac=28\)
ابحث عن رقمين يتم ضربهما في\(ac\)	\((−4)(−7)=28\)
وأضف إلى\(b\).	\(−4(−7)=−11\)
قسّم المدى المتوسط.		$.$
		$.$
ضع في الاعتبار الثلاثي عن طريق التجميع.		$.$
		$.$
تحقق من ذلك بضرب جميع العوامل الثلاثة. \(\hspace{50mm} 5(y−2)(2y−7)\) \(\hspace{45mm} 5(2y^2−7y−4y+14)\) \(\hspace{48mm} 5(2y^2−11y+14)\) \(\hspace{49mm} 10y^2−55y+70\checkmark\)

	$.$
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$
دع\(u=x−2\) واستبدل.	$.$
عامل ثلاثي الحدود.	$.$
استبدل\(u\) بـ\(x−2\).	$.$
قم بالتبسيط داخل الأقواس.	$.$

أهداف التعلم

العوامل: القيم الثلاثية للنموذج\(x^2+bx+c\)

مثال\(\PageIndex{1}\): How to Factor a Trinomial of the form \(x^2+bx+c\)

مثال\(\PageIndex{2}\)

مثال\(\PageIndex{3}\)

مثال\(\PageIndex{4}\)

مثال\(\PageIndex{5}\)

مثال\(\PageIndex{6}\)

مثال\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)

مثال\(\PageIndex{10}\)

مثال\(\PageIndex{11}\)

مثال\(\PageIndex{12}\)

مثال\(\PageIndex{13}\)

مثال\(\PageIndex{14}\)

مثال\(\PageIndex{15}\)

استراتيجية لتخصيم القيم الثلاثية للنموذج\(x^2+bx+c\)

العوامل الثلاثية للنموذج بحد أقصى 2 + مربع+c باستخدام التجربة والخطأ

مثال\(\PageIndex{16}\)

مثال\(\PageIndex{17}\)

مثال\(\PageIndex{18}\)

مثال\(\PageIndex{19}\): How to Factor a Trinomial Using Trial and Error

مثال\(\PageIndex{20}\)

مثال\(\PageIndex{21}\)

عامل الحدود الثلاثية للنموذج\(ax^2+bx+c\) USING TRIAL AND ERROR.

مثال\(\PageIndex{22}\)

مثال\(\PageIndex{23}\)

مثال\(\PageIndex{24}\)

مثال\(\PageIndex{25}\)

مثال\(\PageIndex{26}\)

مثال\(\PageIndex{27}\)

مثال\(\PageIndex{28}\)

مثال\(\PageIndex{29}\)

مثال\(\PageIndex{30}\)

معاملات ثلاثية الحدود للنموذج\(ax^2+bx+c\) باستخدام الطريقة «\(ac\)»

مثال\(\PageIndex{31}\): How to Factor Trinomials using the “ac” Method

مثال\(\PageIndex{32}\)

مثال\(\PageIndex{33}\)

عامل الحدود الثلاثية للنموذج\(ax^2+bx+c\) USING THE “\(ac\)” METHOD.

مثال\(\PageIndex{34}\)

مثال\(\PageIndex{35}\)

مثال\(\PageIndex{36}\)

عامل باستخدام الاستبدال

مثال\(\PageIndex{37}\)

مثال\(\PageIndex{38}\)

مثال\(\PageIndex{39}\)

مثال\(\PageIndex{40}\)

مثال\(\PageIndex{41}\)

مثال\(\PageIndex{42}\)

المفاهيم الرئيسية

العوامل الثلاثية للنموذج بحد أقصى ² + مربع+c باستخدام التجربة والخطأ