4.5: حل أنظمة المعادلات ذات المتغيرات الثلاثة

Last updated
Save as PDF

Page ID: 201467

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

حدِّد ما إذا كان الثلاثي المُرتَّب حلًا لنظام مكوَّن من ثلاث معادلات خطية ذات ثلاثة متغيرات.
حل نظام المعادلات الخطية بثلاثة متغيرات
حل التطبيقات باستخدام أنظمة المعادلات الخطية ذات ثلاثة متغيرات

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

قم بتقييم$5x−2y+3z$ متى$x=−2, y=−4,$$z=3.$
وإذا فاتتك هذه المشكلة، راجع [رابط].
صنّف المعادلات كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل. $ \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. $
إذا فاتتك هذه المشكلة، راجع [link].
صنّف المعادلات كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل. $\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right. $
إذا فاتتك هذه المشكلة، راجع [link].

حدِّد هل الثلاثية المرتبة حلًا لنظام مكوَّن من ثلاث معادلات خطية ذات ثلاثة متغيرات

في هذا القسم، سنقوم بتوسيع عملنا لحل نظام المعادلات الخطية. لقد عملنا حتى الآن مع أنظمة المعادلات بمعادلتين ومتغيرين. الآن سنعمل مع أنظمة من ثلاث معادلات مع ثلاثة متغيرات. ولكن دعونا أولاً نراجع ما نعرفه بالفعل عن حل المعادلات والأنظمة التي تتضمن ما يصل إلى متغيرين.

لقد تعلمنا سابقًا أن الرسم البياني للمعادلة الخطية$ax+by=c$،، هو خط. كل نقطة على الخط، زوج مرتب$(x,y)$، هي حل للمعادلة. بالنسبة لنظام مكون من معادلتين بمتغيرين، نرسم خطين. ثم يمكننا أن نرى أن جميع النقاط التي تمثل حلولًا لكل معادلة تشكل خطًا. ومن خلال إيجاد القواسم المشتركة بين السطور، سنجد الحل للنظام.

تحتوي معظم المعادلات الخطية في متغير واحد على حل واحد، لكننا رأينا أن بعض المعادلات، التي تسمى التناقضات، ليس لها حلول، وبالنسبة للمعادلات الأخرى، التي تسمى الهويات، فإن جميع الأرقام هي حلول

نعلم أنه عندما نحل نظامًا من معادلتين خطيتين ممثلتين برسم بياني لخطين في نفس المستوى، هناك ثلاث حالات محتملة، كما هو موضح.

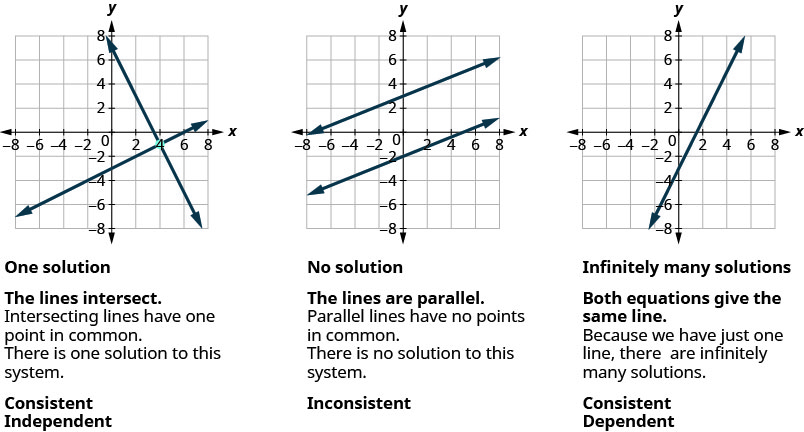
$يوضِّح الشكل ثلاثة رسوم بيانية. في السطر الأول، يتقاطع خطان. تشترك الخطوط المتقاطعة في نقطة واحدة. هناك حل واحد لهذا النظام. تم تسمية الرسم البياني بالاستقلالية المتسقة. في الرسم البياني الثاني، يوجد خطان متوازيان. لا تحتوي الخطوط المتوازية على نقاط مشتركة. لا يوجد حل لهذا النظام. تم تصنيف الرسم البياني بأنه غير متناسق. في الرسم البياني الثالث، يوجد سطر واحد فقط. تعطي كلتا المعادلتين نفس السطر. نظرًا لأن لدينا سطرًا واحدًا فقط، فهناك العديد من الحلول بلا حدود. تم تصنيفها على أنها تعتمد بشكل ثابت.$

وبالمثل، بالنسبة للمعادلة الخطية ذات ثلاثة متغيرات ax+by+cz=d، ax+by+cz=d، فإن كل حل للمعادلة هو ثلاثي مرتب (x، y، z) (x، y، z) يجعل المعادلة صحيحة.

معادلة خطية في ثلاثة متغيرات

معادلة خطية ذات ثلاثة متغيرات، حيث a و b و c و d هي أرقام حقيقية و a و b و c ليست كلها 0، هي من الشكل

\[ ax+by+cz=d\nonumber \]

كل حل للمعادلة هو ثلاثي مرتب، مما$(x,y,z)$ يجعل المعادلة صحيحة.

جميع النقاط التي تمثل حلولًا لمعادلة واحدة تشكل مستوى في الفضاء ثلاثي الأبعاد. ومن خلال إيجاد القواسم المشتركة بين الطائرات، سنجد الحل للنظام.

عندما نحل نظامًا من ثلاث معادلات خطية ممثلة برسم بياني لثلاث مستويات في الفضاء، هناك ثلاث حالات محتملة.

$يتم عرض ثمانية أرقام. تُظهر الصورة الأولى ثلاث مستويات متقاطعة تشترك في نقطة واحدة. يطلق عليه النظام المتسق والمعادلات المستقلة. يحتوي الشكل الثاني على ثلاث مستويات متوازية بدون نقاط مشتركة. يطلق عليه اسم نظام غير متناسق. في الشكل الثالث، هناك طائرتان متزامنتان ومتوازتان مع الطائرة الثالثة. لا توجد نقاط مشتركة بين الطائرات. في الشكل الرابع، هناك طائرتان متوازتان وتتقاطع كل منهما مع المستوى الثالث. لا توجد نقاط مشتركة بين الطائرات. في الشكل الخامس، تتقاطع كل طائرة مع الاثنين الآخرين، لكن الثلاثة لا يتشاركون أي نقاط. لا توجد نقاط مشتركة بين الطائرات. في الشكل السادس، تتقاطع ثلاث طائرات في سطر واحد. هناك سطر واحد فقط، لذلك هناك العديد من الحلول بلا حدود. في الشكل السابع، تتزامن طائرتان وتتقاطعان الطائرة الثالثة في خط. هناك سطر واحد فقط، لذلك هناك العديد من الحلول بلا حدود. في الشكل الأخير، هناك ثلاث طائرات متزامنة. هناك طائرة واحدة فقط، لذلك هناك العديد من الحلول بلا حدود.$ $.$ $.$ $.$ $.$ $.$ $.$ $.$

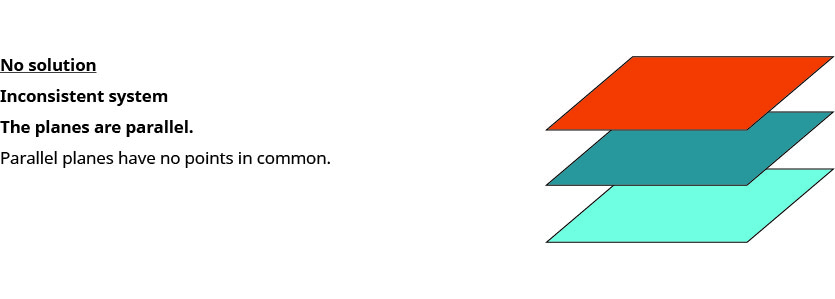
لحل نظام من ثلاث معادلات خطية، نريد إيجاد قيم المتغيرات التي تمثل حلولًا لجميع المعادلات الثلاث. بعبارة أخرى، نحن نبحث عن الثلاثي المرتبة$(x,y,z)$ الذي يجعل المعادلات الثلاث صحيحة. تسمى هذه حلول نظام المعادلات الخطية الثلاث بثلاثة متغيرات.

حلول نظام المعادلات الخطية بثلاثة متغيرات

حلول نظام المعادلات هي قيم المتغيرات التي تجعل جميع المعادلات صحيحة. يتم تمثيل الحل بثلاثية مرتبة$(x,y,z)$.

لتحديد ما إذا كان الثلاثي المرتبة حلاً لنظام مكون من ثلاث معادلات، فإننا نستبدل قيم المتغيرات في كل معادلة. إذا كان الثلاثي المرتبة يجعل المعادلات الثلاث صحيحة، فهذا حل للنظام.

مثال$\PageIndex{1}$

حدد ما إذا كان الثلاثي المطلوب حلاً للنظام:$ \left\{ \begin{array} {l} x−y+z=2 \\ 2x−y−z=−6 \\ 2x+2y+z=−3 \end{array} \right. $

ⓐ$(−2,−1,3)$ ⓑ$(−4,−3,4)$

إجابة

ⓐ

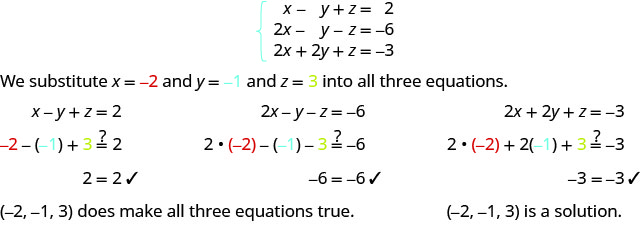
$المعادلات هي x ناقص y زائد z يساوي 2، 2x ناقص y ناقص z يساوي ناقص 6 و 2x زائد 2y زائد z يساوي ناقص 3. باستبدال ناقص 2 بـ x، وناقص 1 لـ y، و3 لـ z في جميع المعادلات الثلاث، نجد أن جميع المعادلات الثلاث صحيحة. وبالتالي، فإن ناقص 2، ناقص 1، 3 هو الحل.$

ⓑ

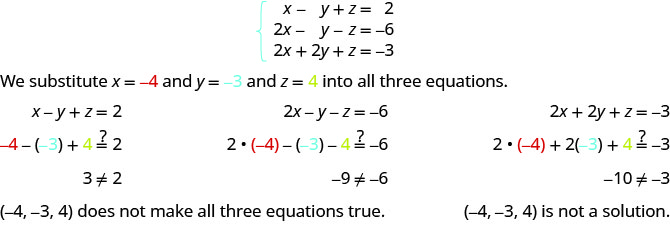
$المعادلات هي x ناقص y زائد z يساوي 2، 2x ناقص y ناقص z يساوي ناقص 6 و 2x زائد 2y زائد z يساوي ناقص 3. باستبدال ناقص 4 لـ x، ناقص 3 لـ y و 4 لـ z في جميع المعادلات الثلاث، نجد أن جميع المعادلات الثلاث صحيحة. وبالتالي، فإن ناقص 4، ناقص 3، 4 ليس حلاً.$

مثال$\PageIndex{2}$

حدد ما إذا كان الثلاثي المطلوب حلاً للنظام:$ \left\{ \begin{array} {l} 3x+y+z=2 \\ x+2y+z=−3 \\ 3x+y+2z=4 \end{array} \right. $

ⓐ$(1,−3,2)$ ⓑ$(4,−1,−5)$

إجابة: ⓐ نعم ⓑ لا

مثال$\PageIndex{3}$

حدد ما إذا كان الثلاثي المطلوب حلاً للنظام:$ \left\{ \begin{array} {l} x−3y+z=−5 \\ −3x−y−z=1 \\ 2x−2y+3z=1 \end{array} \right. $

ⓐ$(2,−2,3)$ ⓑ$(−2,2,3)$

إجابة: ⓐ لا ⓑ نعم

حل نظام المعادلات الخطية بثلاثة متغيرات

لحل نظام المعادلات الخطية بثلاثة متغيرات، نستخدم بشكل أساسي نفس الأساليب التي استخدمناها مع الأنظمة التي تحتوي على متغيرين. نبدأ بزوجين من المعادلات وفي كل زوج نزيل نفس المتغير. سيعطينا هذا بعد ذلك نظامًا من المعادلات بمتغيرين فقط ثم نعرف كيفية حل هذا النظام!

بعد ذلك، نستخدم قيم المتغيرين اللذين وجدناهما للتو للعودة إلى المعادلة الأصلية والعثور على المتغير الثالث. نكتب إجابتنا كثلاثية مرتبة ثم نتحقق من نتائجنا.

مثال$\PageIndex{4}$: How to Solve a System of Equations With Three Variables by Elimination

حل النظام عن طريق الإزالة:$ \left\{ \begin{array} {l} x−2y+z=3 \\ 2x+y+z=4 \\ 3x+4y+3z=−1 \end{array} \right. $

إجابة: $المعادلات هي x ناقص 2y زائد z يساوي 3، 2x زائد y زائد z يساوي 4 و 3x زائد 4y زائد 3z يساوي ناقص 1. الخطوة 1 هي كتابة المعادلات في النموذج القياسي. هم هم. إذا كانت أي معاملات عبارة عن كسور، فقم بإزالتها. لا يوجد أحد.$ $الخطوة 2 هي إزالة نفس المتغير من معادلتين. حدد المتغير الذي ستقوم بإزالته. يمكننا حذف y من المعادلات 1 و 2 بضرب المعادلة 2 في 2. اعمل باستخدام زوج من المعادلات لإزالة المتغير المختار. اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد. أضف المعادلات الناتجة من الخطوة 2 لإزالة متغير واحد. المعادلة الجديدة التي نحصل عليها هي 5x زائد 3z تساوي 11.$ $الخطوة 3 هي تكرار الخطوة 2 باستخدام معادلتين أخريين وإزالة نفس المتغير كما في الخطوة 2. يمكننا مرة أخرى إزالة y باستخدام المعادلات 1، 3 بضرب المعادلة 1 في 2. أضف المعادلات الجديدة وستكون النتيجة 5x زائد 5z تساوي 5.$ $الخطوة 4. تشكل المعادلتين الجديدتين نظامًا من معادلتين بمتغيرين. حل هذا النظام. بعد إزالة x، نحصل على z يساوي ناقص 3. باستبدال هذا في إحدى المعادلات الجديدة، نحصل على x يساوي 4.$ $الخطوة 5 هي استخدام قيم المتغيرين الموجودين في الخطوة 4 للعثور على المتغير الثالث. 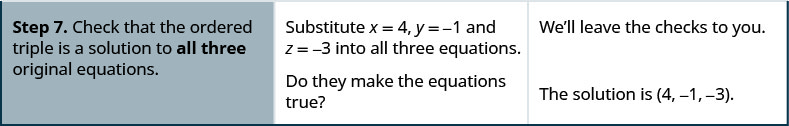باستبدال قيم x و z في إحدى المعادلات الأصلية، نحصل على y يساوي ناقص 1.$ $الخطوة 6 هي كتابة الحل كثلاثي مرتب 4، ناقص 1، ناقص 3.$ $الخطوة 7 هي التحقق من أن الثلاثية المرتبة هي الحل لجميع المعادلات الأصلية الثلاث. يجعل جميع المعادلات الثلاث صحيحة.$

مثال$\PageIndex{5}$

حل النظام عن طريق الإزالة:$ \left\{ \begin{array} {l} 3x+y−z=2 \\ 2x−3y−2z=1 \\ 4x−y−3z=0 \end{array} \right.$

إجابة: $(2,−1,3)$

مثال$\PageIndex{6}$

حل النظام عن طريق الإزالة:$ \left\{ \begin{array} {l} 4x+y+z=−1 \\ −2x−2y+z=2 \\ 2x+3y−z=1 \end{array} \right. $

إجابة: $(−2,3,4)$

يتم تلخيص الخطوات هنا.

حل نظام المعادلات الخطية بثلاثة متغيرات.

اكتب المعادلات في الصورة القياسية
- إذا كانت أي معاملات عبارة عن كسور، فقم بإزالتها.
احذف نفس المتغير من معادلتين.
- حدد المتغير الذي ستقوم بإزالته.
- اعمل باستخدام زوج من المعادلات لإزالة المتغير المختار.
- اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد.
- أضف المعادلات الناتجة من الخطوة 2 لإزالة متغير واحد
كرر الخطوة 2 باستخدام معادلتين أخريين وقم بإزالة نفس المتغير كما في الخطوة 2.
تشكل المعادلتين الجديدتين نظامًا من معادلتين بمتغيرين. حل هذا النظام.
استخدم قيم المتغيرين الموجودين في الخطوة 4 للعثور على المتغير الثالث.
اكتب الحل في صورة ثلاثية مرتبة.
تأكد من أن الثلاثية المرتبة هي الحل لجميع المعادلات الأصلية الثلاث.

مثال$\PageIndex{7}$

حل:$ \left\{ \begin{array} {l} 3x−4z=0 \\ 3y+2z=−3 \\ 2x+3y=−5 \end{array} \right. $

إجابة

\[ \left\{ \begin{array} {ll} 3x−4z=0 &(1) \\ 3y+2z=−3 &(2) \\ 2x+3y=−5 &(3) \end{array} \right. \nonumber \]

يمكننا الحذف$z$ من المعادلات (1) و (2) بضرب المعادلة (2) في 2 ثم إضافة المعادلات الناتجة.

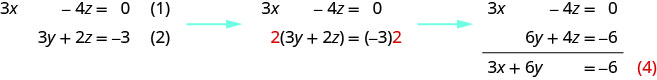
$المعادلات هي 3 × ناقص 4 يساوي 0، 3y زائد 2 z يساوي ناقص 3 و 2 x زائد 3 y يساوي ناقص 5. اضرب المعادلة 2 في 2 وأضف إلى المعادلة 1. نحصل على 3 × زائد 6 ص يساوي ناقص 6.$

لاحظ أن المعادلتين (3) و (4) تحتويان على المتغيرات$x$ و$y$. سنحل هذا النظام الجديد لـ$x$ و$y$.

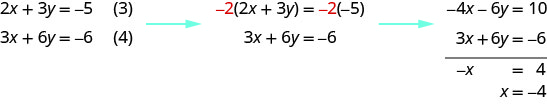
$اضرب المعادلة 3 في ناقص 2 وأضف ذلك إلى المعادلة 4. نحصل على x يساوي ناقص 4.$

لحل y، نستبدل$x=−4$ المعادلة (3).

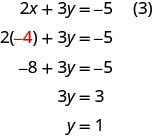
$استبدل ناقص 4 في المعادلة 3 وحل لـ y. نحصل على y يساوي 1.$

لدينا الآن$x=−4$ و$y=1$. نحن بحاجة إلى حل مشكلة z. يمكننا استبدال$x=−4$ المعادلة (1) للعثور على z.

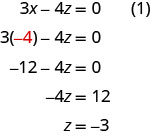
$باستبدال ناقص 4 في المعادلة 1 لـ x، نحصل على z يساوي ناقص 3.$

نكتب الحل كثلاثية مرتبة. $(−4,1,−3)$

نتحقق من أن الحل يجعل جميع المعادلات الثلاث صحيحة.

$\begin{array} {lll} {3x-4z=0 \space (1)} &{3y+2z=−3 \space (2)} &{2x+3y=−5 \space (3)} \\ {3(−4)−4(−3)\overset{?}{=} 0} &{3(1)+2(−3)\overset{?}{=} −3} &{2(−4)+3(1)\overset{?}{=} −5} \\ {0=0 \checkmark} &{−3=−3 \checkmark} &{−5=−5 \checkmark} \\ {} &{} &{\text{The solution is }(−4,1,−3)} \end{array}$

مثال$\PageIndex{8}$

حل:$ \left\{ \begin{array} {l} 3x−4z=−1 \\ 2y+3z=2 \\ 2x+3y=6 \end{array} \right. $

إجابة: $(−3,4,−2)$

مثال$\PageIndex{9}$

حل:$ \left\{ \begin{array} {l} 4x−3z=−5 \\ 3y+2z=7 \\ 3x+4y=6 \end{array} \right. $

إجابة: $(−2,3,−1)$

عندما نحل نظامًا وينتهي بنا الأمر بدون متغيرات وبيان خاطئ، فإننا نعلم أنه لا توجد حلول وأن النظام غير متسق. يوضح المثال التالي نظام المعادلات غير المتسق.

مثال$\PageIndex{10}$

حل نظام المعادلات:$ \left\{ \begin{array} {l} x+2y−3z=−1 \\ x−3y+z=1 \\ 2x−y−2z=2 \end{array} \right. $

إجابة

\[\left\{ \begin{array} {ll} x+2y−3z=−1 &(1) \\ x−3y+z=1 &(2) \\ 2x−y−2z=2 &(3) \end{array} \right.\nonumber \]

استخدم المعادلة (1) و (2) لإزالة z.

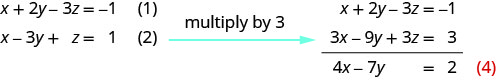
$المعادلات هي x زائد 2y ناقص 3z يساوي ناقص 1، x ناقص 3y زائد z يساوي 1 و 2x ناقص y ناقص 2z يساوي 2.$

استخدم (2) و (3) للتخلص$z$ مرة أخرى.

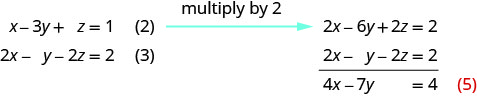
$بضرب المعادلة 2 في 3 وإضافتها إلى المعادلة 1، نحصل على المعادلة 4، 4x ناقص 7y يساوي 2. بضرب المعادلة 2 في 2 وإضافتها إلى المعادلة 3، نحصل على المعادلة 5، 4x ناقص 7y يساوي 4.$

استخدم (4) و (5) لإزالة متغير.

$تحتوي كل من المعادلتين 4 و5 على متغيرين. اضرب المعادلة 5 في ناقص 1 وأضفها إلى المعادلة 4. نحصل على 0 يساوي ناقص 2، وهو خطأ.$

لا يوجد حل.

لقد تركنا بيانًا خاطئًا وهذا يخبرنا أن النظام غير متسق وليس له حل.

مثال$\PageIndex{11}$

حل نظام المعادلات:$ \left\{ \begin{array} {l} x+2y+6z=5 \\ −x+y−2z=3 \\ x−4y−2z=1 \end{array} \right. $

إجابة: لا يوجد حل

مثال$\PageIndex{12}$

حل نظام المعادلات:$ \left\{ \begin{array} {l} 2x−2y+3z=6 \\ 4x−3y+2z=0 \\ −2x+3y−7z=1 \end{array} \right. $

إجابة: لا يوجد حل

عندما نحل نظامًا وننتهي بدون متغيرات سوى بيان حقيقي، فإننا نعلم أن هناك العديد من الحلول بلا حدود. يتوافق النظام مع المعادلات التابعة. سيوضح حلنا كيف يعتمد اثنان من المتغيرات على الثالث.

مثال$\PageIndex{13}$

حل نظام المعادلات:$ \left\{ \begin{array} {l} x+2y−z=1 \\ 2x+7y+4z=11 \\ x+3y+z=4 \end{array} \right. $

إجابة

\[\left\{ \begin{array} {ll} x+2y−z=1 &(1) \\ 2x+7y+4z=11 &(2) \\ x+3y+z=4 &(3) \end{array} \right.\nonumber \]

استخدم المعادلة (1) و (3) لإزالة x.

$المعادلات هي x زائد 2y ناقص z يساوي 1، 2x زائد 7y زائد 4z يساوي 11 و x زائد 3y زائد z يساوي 4. اضرب المعادلة 1 مع ناقص 1 وأضفها إلى المعادلة 3. نحصل على المعادلة 4، y زائد 2z يساوي 3.$

استخدم المعادلة (1) و (2) لإزالة x مرة أخرى.

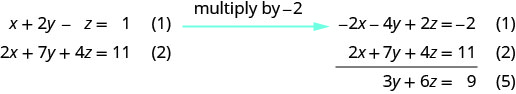
$اضرب المعادلة 1 مع ناقص 2 وأضفها إلى المعادلة 2. نحصل على المعادلة 5، 3y زائد 6z يساوي 9.$

استخدم المعادلة (4) و (5) للقضاء$y$.

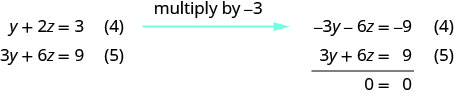
$اضرب المعادلة 4 مع ناقص 3 وأضفها إلى المعادلة 5. نحصل على 0 يساوي 0. هناك العديد من الحلول التي لا حصر لها. بحل المعادلة 4 لـ y، نحصل على y يساوي ناقص 2z زائد 3. باستبدال هذا بالمعادلة 1، نحصل على x يساوي 5z ناقص 5. تخبرنا العبارة الحقيقية 0 التي تساوي 0 أن هذا نظام تابع يحتوي على العديد من الحلول بلا حدود. الحلول هي من النموذج x و y و z حيث x هو 5z ناقص 5 و y هو ناقص 2z زائد 3 و z هو أي رقم حقيقي.$

	هناك العديد من الحلول بلا حدود.
حل المعادلة (4) لـ y.	قم بتمثيل الحل الذي يوضح كيف تعتمد x و y على z. $ \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} $
استخدم المعادلة (1) لحل x.	$ x+2y−z=1$
بديل$y=−2z+3$.	$ \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} $

$0=0$يخبرنا البيان الحقيقي أن هذا نظام تابع يحتوي على العديد من الحلول بلا حدود. الحلول هي من النموذج (x، y، z) (x، y، z) حيث$x=5z−5;\space y=−2z+3$ و z هو أي رقم حقيقي.

مثال$\PageIndex{14}$

حل النظام عن طريق المعادلات:$ \left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. $

إجابة: العديد من الحلول بلا حدود$(x,3,z)$ أين$x=z−3;\space y=3;\space z$ يوجد أي رقم حقيقي

مثال$\PageIndex{15}$

حل النظام عن طريق المعادلات:$ \left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. $

إجابة: العديد من الحلول بلا حدود$(x,y,z)$ أين$x=5z−2;\space y=4z−3;\space z$ يوجد أي رقم حقيقي

حل التطبيقات باستخدام أنظمة المعادلات الخطية ذات المتغيرات الثلاثة

يمكن حل التطبيقات التي تم تصميمها بواسطة أنظمة المعادلات باستخدام نفس التقنيات التي استخدمناها لحل الأنظمة. العديد من التطبيقات هي مجرد ملحقات لثلاثة متغيرات من الأنواع التي قمنا بحلها سابقًا.

مثال$\PageIndex{16}$

باع قسم المسرح بالكلية المجتمعية ثلاثة أنواع من التذاكر لأحدث إنتاج مسرحي. تم بيع تذاكر البالغين مقابل 15 دولارًا، وتذاكر الطلاب مقابل 10 دولارات، وتذاكر الأطفال مقابل 8 دولارات. كان قسم المسرح سعيدًا ببيع 250 تذكرة وجلب 2,825 دولارًا في ليلة واحدة. عدد تذاكر الطلاب المباعة هو ضعف عدد تذاكر البالغين المباعة. كم من كل نوع قام القسم ببيعه؟

إجابة

سنستخدم مخططًا لتنظيم المعلومات.	$.$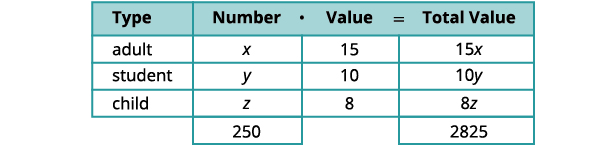
عدد الطلاب هو ضعف عدد البالغين.
أعد كتابة المعادلة في النموذج القياسي.	$\begin{aligned} y &= 2x \\ 2x−y &= 0 \end{aligned} $
$.$
استخدم المعادلات (1) و (2) لإزالة z.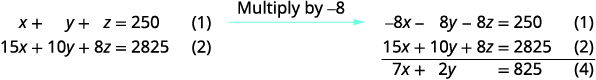
$.$
استخدم (3) و (4) للقضاء$y$.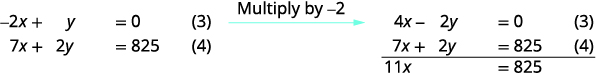
$.$
حل لـ x.	$x=75 $تذاكر للبالغين
استخدم المعادلة (3) للعثور على y.	$−2x+y=0$
بديل$x=75$.	$\begin{aligned} −2(75)+y &= 0 \\ −150+y &= 0 \\ y &= 150\text{ student tickets}\end{aligned} $
استخدم المعادلة (1) للعثور على z.	$x+y+z=250$
استبدل القيم $x=75, \space y=150.$	$\begin{aligned} 75+150+z &= 250 \\ 225+z &= 250 \\ z &= 25\text{ child tickets} \end{aligned} $
اكتب الحل.	باع قسم المسرح 75 تذكرة للبالغين و 150 تذكرة طالب و 25 تذكرة للأطفال.

مثال$\PageIndex{17}$

باع قسم الفنون الجميلة بكلية المجتمع ثلاثة أنواع من التذاكر لأحدث عرض رقص. تم بيع تذاكر البالغين مقابل 20 دولارًا، وتذاكر الطلاب مقابل 12 دولارًا، وتذاكر الأطفال مقابل 10 دولارات. كان قسم الفنون الجميلة سعيدًا ببيع 350 تذكرة وجلب 4,650 دولارًا في ليلة واحدة. عدد تذاكر الأطفال المباعة هو نفس عدد تذاكر البالغين المباعة. كم من كل نوع قام القسم ببيعه؟

إجابة: باع قسم الفنون الجميلة 75 تذكرة للبالغين و 200 تذكرة للطلاب و 75 تذكرة للأطفال.

مثال$\PageIndex{18}$

باع فريق كرة القدم بالكلية المجتمعية ثلاثة أنواع من التذاكر لأحدث لعبة. تم بيع تذاكر البالغين مقابل 10 دولارات وتذاكر الطلاب مقابل 8 دولارات وتذاكر الأطفال مقابل 5 دولارات. شعر فريق كرة القدم بسعادة غامرة لأنه باع 600 تذكرة وجلب 4,900 دولار لمباراة واحدة. عدد تذاكر البالغين هو ضعف عدد تذاكر الأطفال. كم من كل نوع قام فريق كرة القدم ببيعه؟

إجابة: باع فريق كرة القدم 200 تذكرة للبالغين و 300 تذكرة للطلاب و 100 تذكرة للأطفال.

يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل نظام خطي في ثلاثة متغيرات بدون حلول أو حلول غير محدودة.

حل نظام خطي في ثلاثة متغيرات باستخدام حلول بلا حلول أو حلول غير محدودة
3 تطبيق متغير

المفاهيم الرئيسية

المعادلة الخطية في ثلاثة متغيرات: معادلة خطية ذات ثلاثة متغيرات، حيث a و b و c و d هي أرقام حقيقية و a و b و c ليست كلها 0، هي من الشكل
\[ax+by+cz=d\nonumber \]

كل حل للمعادلة هو ثلاثي مرتب، مما$(x,y,z)$ يجعل المعادلة صحيحة.
كيفية حل نظام المعادلات الخطية بثلاثة متغيرات.
1. اكتب المعادلات في الصورة القياسية
  إذا كانت أي معاملات عبارة عن كسور، فقم بإزالتها.
2. احذف نفس المتغير من معادلتين.
  حدد المتغير الذي ستقوم بإزالته.
  اعمل باستخدام زوج من المعادلات لإزالة المتغير المختار.
  اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد.
  أضف المعادلات الناتجة من الخطوة 2 لإزالة متغير واحد
3. كرر الخطوة 2 باستخدام معادلتين أخريين وقم بإزالة نفس المتغير كما في الخطوة 2.
4. تشكل المعادلتين الجديدتين نظامًا من معادلتين بمتغيرين. حل هذا النظام.
5. استخدم قيم المتغيرين الموجودين في الخطوة 4 للعثور على المتغير الثالث.
6. اكتب الحل في صورة ثلاثية مرتبة.
7. تأكد من أن الثلاثية المرتبة هي الحل لجميع المعادلات الأصلية الثلاث.

مسرد المصطلحات

حلول نظام المعادلات الخطية مع ثلاثة متغيرات: حلول نظام المعادلات هي قيم المتغيرات التي تجعل جميع المعادلات صحيحة؛ يتم تمثيل الحل بثلاثية مرتبة (x، y، z).

	هناك العديد من الحلول بلا حدود.
حل المعادلة (4) لـ y.	قم بتمثيل الحل الذي يوضح كيف تعتمد x و y على z. \( \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} \)
استخدم المعادلة (1) لحل x.	\( x+2y−z=1\)
بديل\(y=−2z+3\).	\( \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} \)

معادلة خطية في ثلاثة متغيرات

حلول نظام المعادلات الخطية بثلاثة متغيرات

مثال\(\PageIndex{1}\)

مثال\(\PageIndex{2}\)

مثال\(\PageIndex{3}\)

مثال\(\PageIndex{4}\): How to Solve a System of Equations With Three Variables by Elimination

مثال\(\PageIndex{5}\)

مثال\(\PageIndex{6}\)

حل نظام المعادلات الخطية بثلاثة متغيرات.

مثال\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)

مثال\(\PageIndex{10}\)

مثال\(\PageIndex{11}\)

مثال\(\PageIndex{12}\)

مثال\(\PageIndex{13}\)

مثال\(\PageIndex{14}\)

مثال\(\PageIndex{15}\)

مثال\(\PageIndex{16}\)

مثال\(\PageIndex{17}\)

مثال\(\PageIndex{18}\)