الفصل 3 تمارين المراجعة

تمارين مراجعة الفصل

رسم بياني للمعادلات الخطية في متغيرين

رسم النقاط في نظام الإحداثيات المستطيلة

في التمارين التالية، ارسم كل نقطة في نظام إحداثيات مستطيل.

1. ⓐ$(−1,−5)$
ⓑ$(−3,4)$
ⓒ$(2,−3)$
ⓓ$(1,\frac{5}{2})$

إجابة

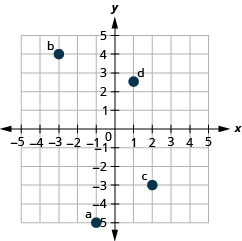
2. ⓐ$(−2,0)$
ⓑ$(0,−4)$
ⓒ$(0,5)$
ⓓ$(3,0)$

في التمارين التالية، حدد الأزواج المرتبة التي تمثل حلولًا للمعادلات المعطاة.

3. $5x+y=10$؛

ⓐ$(5,1)$
ⓑ$(2,0)$
ⓒ$(4,−10)$

إجابة

ⓑ، ⓒ

4. $y=6x−2$؛

ⓐ$(1,4)$
ⓑ$(13,0)$
ⓒ$(6,−2)$

رسم معادلة خطية بيانيًا عن طريق رسم النقاط

في التمارين التالية، قم بالرسم البياني عن طريق رسم النقاط.

5. $y=4x−3$

إجابة

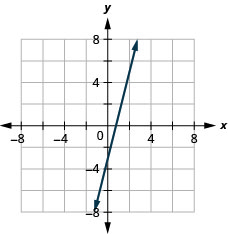
6. $y=−3x$

7. $y=\frac{1}{2}x+3$

إجابة

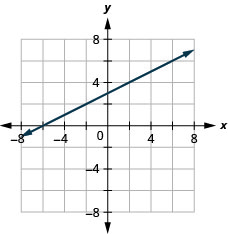
8. $y=−\frac{4}{5}|x−1$

9. $x−y=6$

إجابة

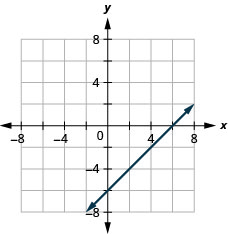
10. $2x+y=7$

11. $3x−2y=6$

إجابة

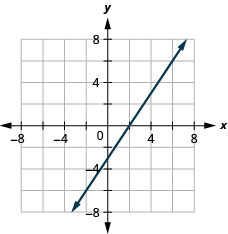
رسم بياني: خطوط عمودية وأفقية

في التمارين التالية، قم برسم بياني لكل معادلة.

12. $y=−2$

13. $x=3$

إجابة

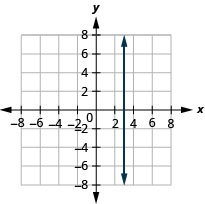
في التمارين التالية، قم برسم بياني لكل زوج من المعادلات في نفس نظام الإحداثيات المستطيلة.

14. $y=−2x$و$y=−2$

15. $y=\frac{4}{3}x$و$y=\frac{4}{3}$

إجابة

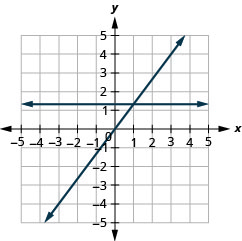
ابحث عن عمليات الاعتراض x و y

في التمارين التالية، ابحث عن نقاط التقاطع x - و y.

16.

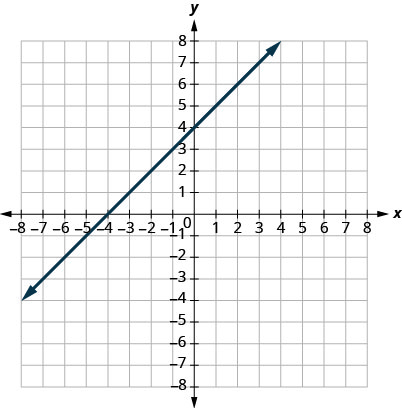
17.

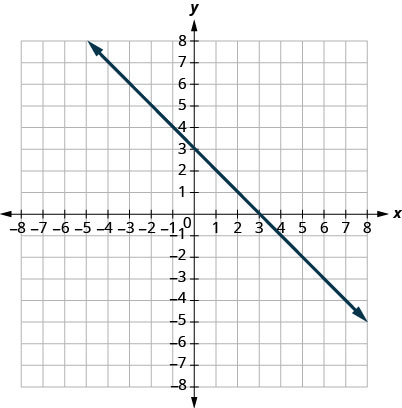
إجابة

$(0,3)(3,0)$

في التمارين التالية، ابحث عن الأجزاء المقطوعة لكل معادلة.

18. $x−y=−1$

19. $x+2y=6$

إجابة

$(6,0),\space (0,3)$

20. $2x+3y=12$

21. $y=\frac{3}{4}x−12$

إجابة

$(16,0),\space (0,−12)$

22. $y=3x$

ارسم خطًا بيانيًا باستخدام القطع المقطوعة

في التمارين التالية، قم بالرسم البياني باستخدام عمليات الاعتراض.

23. $−x+3y=3$

إجابة

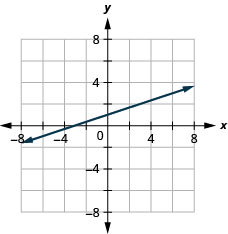
24. $x−y=4$

25. $2x−y=5$

إجابة

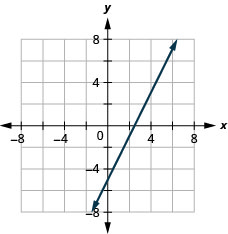
26. $2x−4y=8$

27. $y=4x$

إجابة

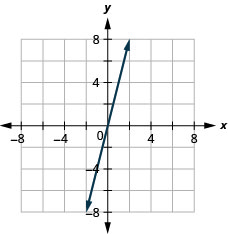
ميل الخط

أوجد ميل الخط المستقيم

في التمارين التالية، أوجد ميل كل خط موضَّح.

28.

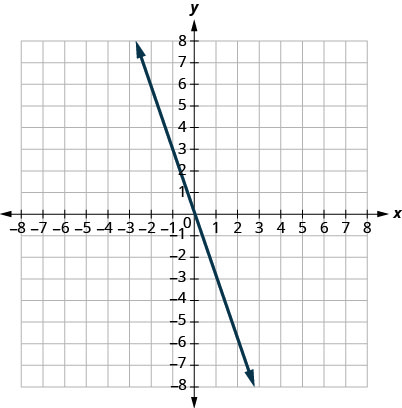
29.

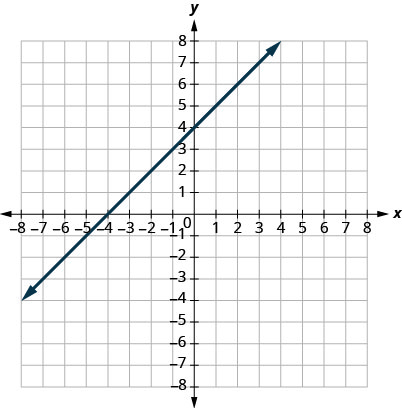
إجابة

1

30.

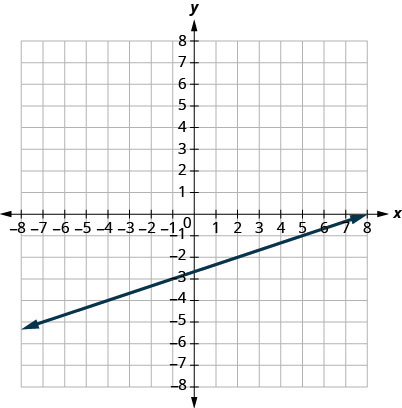
31.

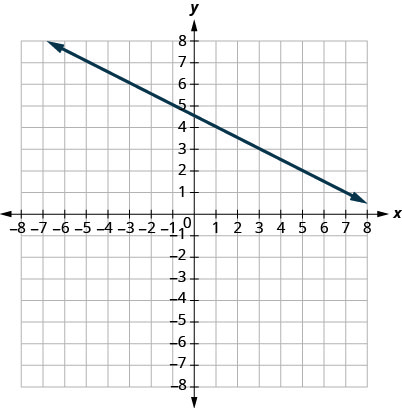
إجابة

$−12$

في التمارين التالية، ابحث عن ميل كل خط.

32. $y=2$

33. $x=5$

إجابة

غير محدد

34. $x=−3$

35. $y=−1$

إجابة

0

استخدم صيغة المنحدر للعثور على ميل الخط الفاصل بين نقطتين

في التمارين التالية، استخدم صيغة المنحدر للعثور على ميل الخط الفاصل بين كل زوج من النقاط.

36. $(−1,−1),(0,5)$

37. $(3.5),(4,−1)$

إجابة

$−6$

38. $(−5,−2),(3,2)$

39. $(2,1),(4,6)$

إجابة

$52$

رسم بياني للخط المستقيم بمعلومية النقطة والمنحدر

في التمارين التالية، قم برسم بياني لكل خط بالنقطة والمنحدر الموضحين.

40. $(2,−2);\space m=52$

41. $(−3,4);\space m=−13$

إجابة

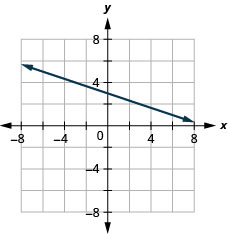
42. $x$-اعتراض$−4; m=3$

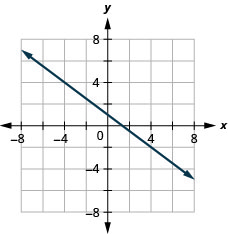
43. $y$-اعتراض$1; m=−34$

إجابة

رسم خط مستقيم باستخدام ميله والجزء المقطوع منه

في التمارين التالية، حدد المنحدر$y$ والجزء المقطوع لكل خط.

44. $y=−4x+9$

45. $y=53x−6$

إجابة

$m=53;\space (0,−6)$

46. $5x+y=10$

47. $4x−5y=8$

إجابة

$m=\frac{4}{5};\space (0,−\frac{8}{5})$

في التمارين التالية، قم برسم خط كل معادلة بيانيًا باستخدام المنحدر والجزء المقطوع من y.

48. $y=2x+3$

49. $y=−x−1$

إجابة

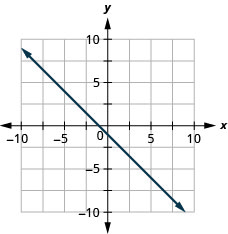
50. $y=−25x+3$

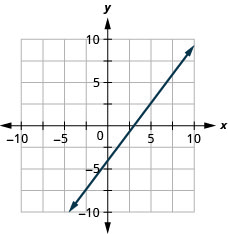
51. $4x−3y=12$

إجابة

في التمارين التالية، حدد الطريقة الأكثر ملاءمة لرسم كل سطر.

52. $x=5$

53. $y=−3$

إجابة

خط أفقي

54. $2x+y=5$

55. $x−y=2$

إجابة

عمليات الاعتراض

56. $y=22x+2$

57. $y=34x−1$

إجابة

نقاط التخطيط

رسم بياني وتفسير تطبيقات التقاطع المنحدر

58. كاثرين هي طاهية خاصة. $C=6.5m+42$تُمثِّل المعادلة العلاقة بين تكلفتها الأسبوعية، C، بالدولار وعدد الوجبات، m، التي تقدمها.

ⓐ ابحث عن تكلفة كاثرين لمدة أسبوع عندما لا تقدم أي وجبات.
ⓑ ابحث عن التكلفة لمدة أسبوع عندما تقدم 14 وجبة.
ⓒ قم بتفسير المنحدر والجزء C من المعادلة.
ⓓ رسم المعادلة بيانيًا.

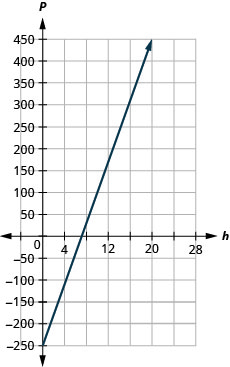
59. مارجوري تدرس العزف على البيانو. $P=35h−250$تُمثل المعادلة العلاقة بين ربحها الأسبوعي، P، بالدولار وعدد دروس الطلاب التي تدرسها.

ⓐ ابحث عن ربح مارجوري لمدة أسبوع عندما لا تدرس دروسًا للطلاب.
ⓑ احصل على الربح لمدة أسبوع عندما تقوم بتدريس 20 درسًا للطلاب.
ⓒ قم بتفسير المنحدر والجزء المقطوع من النقطة P للمعادلة.
ⓓ رسم المعادلة بيانيًا.

إجابة

ⓐ$−$250$
ⓑ$$450$
ⓒ المنحدر، 35، يعني أن ربح مارجوري الأسبوعي، P، يزيد بمقدار 35 دولارًا لكل درس إضافي تقوم بتدريسه للطالب.
يعني P -Intercept أنه عندما يكون عدد الدروس 0، تخسر مارجوري 250 دولارًا.
ⓓ

استخدم المنحدرات لتحديد الخطوط المستقيمة المتوازية والمتعامدة

في التمارين التالية، استخدم المنحدرات$y$ ونقاط التقاطع لتحديد ما إذا كانت الخطوط متوازية أو عمودية أم لا.

60. $4x−3y=−1;\quad y=43x−3$

61. $y=5x−1;\quad 10x+2y=0$

إجابة

ولا

62. $3x−2y=5;\quad 2x+3y=6$

63. $2x−y=8;\quad x−2y=4$

إجابة

غير متوازي

أوجد معادلة الخط المستقيم

أوجد معادلة الخط المستقيم بمعلومية المنحدر والجزء المقطوع من محور الصادات

في التمارين التالية، أوجد معادلة الخط المستقيم الذي يحتوي على ميل معطى والجزء المقطوع من محور الصادات. اكتب المعادلة في صورة منحدر-مقطع.

64. المنحدر$\frac{1}{3}$$y$ والاعتراض$(0,−6)$

65. المنحدر$−5$$y$ والاعتراض$(0,−3)$

إجابة

$y=−5x−3$

66. المنحدر$0$$y$ والاعتراض$(0,4)$

67. المنحدر$−2$$y$ والاعتراض$(0,0)$

إجابة

$y=−2x$

في التمارين التالية، ابحث عن معادلة الخط المستقيم الموضح في كل رسم بياني. اكتب المعادلة في صورة منحدر-مقطع.

68.

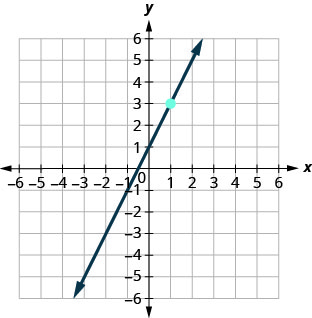
69.

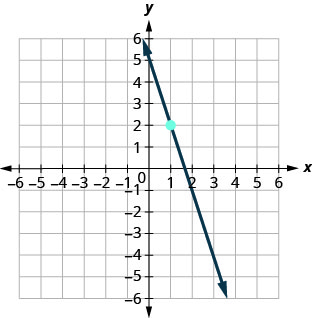
إجابة

$y=−3x+5$

70.

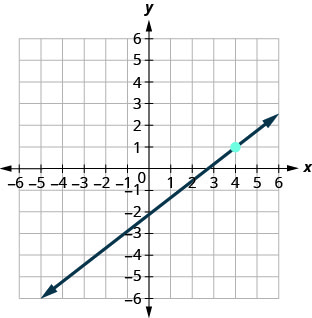
71.

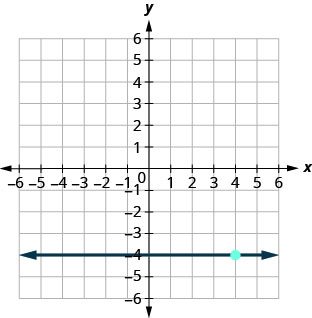
إجابة

$y=−4$

أوجد معادلة الخط المستقيم بمعلومية الميل والنقطة

في التمارين التالية، أوجد معادلة الخط المستقيم الذي يحتوي على ميل معطى ويحتوي على النقطة المُعطاة. اكتب المعادلة في صورة منحدر-مقطع.

72. $m=−\frac{1}{4}$، نقطة$(−8,3)$

73. $m=\frac{3}{5}$، نقطة$(10,6)$

إجابة

$y=\frac{3}{5}x$

74. خط أفقي يحتوي على$(−2,7)$

75. $m=−2$، نقطة$(−1,−3)$

إجابة

$y=−2x−5$

أوجد معادلة الخط المستقيم بمعلومية نقطتين

في التمارين التالية، أوجد معادلة الخط الذي يحتوي على النقاط المُعطاة. اكتب المعادلة في صورة منحدر-مقطع.

76. $(2,10)$و$(−2,−2)$

77. $(7,1)$و$(5,0)$

إجابة

$y=\frac{1}{2}x−\frac{5}{2}$

78. $(3,8)$و$(3,−4)$

79. $(5,2)$و$(−1,2)$

إجابة

$y=2$

ابحث عن معادلة الخط المستقيم الموازي لخط مُعطًى

في التمارين التالية، أوجد معادلة الخط المستقيم الموازي للخط المُعطى، ويحتوي على النقطة المُعطاة. اكتب المعادلة في صورة منحدر-مقطع.

80. خط$y=−3x+6$، نقطة$(1,−5)$

81. خط$2x+5y=−10$، نقطة$(10,4)$

إجابة

$y=−\frac{2}{5}x+8$

82. خط$x=4$، نقطة$(−2,−1)$

83. خط$y=−5$، نقطة$(−4,3)$

إجابة

$y=3$

ابحث عن معادلة خط مستقيم عمودي على خط مُعطًى

في التمارين التالية، ابحث عن معادلة الخط المستقيم المتعامد على الخط المعطى وتحتوي على النقطة المُعطاة. اكتب المعادلة في صورة منحدر-مقطع.

84. خط$y=−\frac{4}{5}x+2$، نقطة$(8,9)$

85. خط$2x−3y=9$، نقطة$(−4,0)$

إجابة

$y=−\frac{3}{2}x−6$

86. سطر$y=3$، نقطة$(−1,−3)$

87.$x=−5$ نقطة خط$(2,1)$

إجابة

$y=1$

رسم بياني متباينات خطية في متغيرين

تحقق من حلول عدم المساواة في متغيرين

في التمارين التالية، حدد ما إذا كان كل زوج مرتب يمثل حلاً لعدم المساواة المعطاة.

88. حدد ما إذا كان كل زوج مرتب حلاً لعدم المساواة$y<x−3$:

ⓐ$(0,1)$ ⓑ$(−2,−4)$ ⓒ$(5,2)$ ⓓ$(3,−1)$
ⓔ$(−1,−5)$

89. حدد ما إذا كان كل زوج مرتب حلاً لعدم المساواة$x+y>4$:

ⓐ$(6,1)$ ⓑ$(−3,6)$ ⓒ$(3,2)$ ⓓ$(−5,10)$ ⓔ$(0,0)$

إجابة

ⓐ نعم ⓑ لا ⓒ نعم ⓓ نعم؛ ⓔ نوم

تعرف على العلاقة بين حلول عدم المساواة ورسمها البياني

في التمارين التالية، اكتب عدم المساواة التي تظهرها المنطقة المظللة.

90. اكتب عدم المساواة التي يوضحها الرسم البياني مع خط الحدود$y=−x+2.$

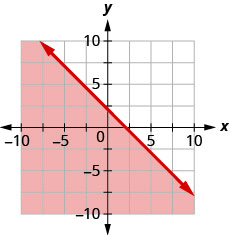
91. اكتب عدم المساواة التي يوضحها الرسم البياني مع خط الحدود$y=\frac{2}{3}x−3$.

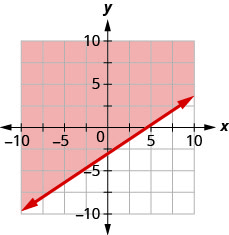
إجابة

$y>\frac{2}{3}x−3$

92. اكتب عدم المساواة التي تظهرها المنطقة المظللة في الرسم البياني مع خط الحدود$x+y=−4$.

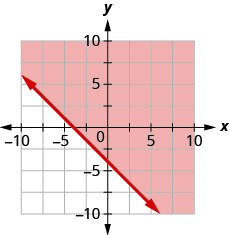
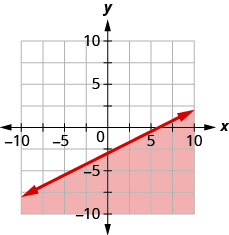
93. اكتب عدم المساواة التي تظهرها المنطقة المظللة في الرسم البياني مع خط الحدود$x−2y=6$.

إجابة

$x−2y\geq 6$

رسم بياني متباينات خطية في متغيرين

في التمارين التالية، قم برسم بياني لكل تفاوت خطي.

94. رسم بياني للتفاوت الخطي$y>\frac{2}{5}x−4$.

95. رسم بياني للتفاوت الخطي$y\leq −\frac{1}{4}x+3$.

إجابة

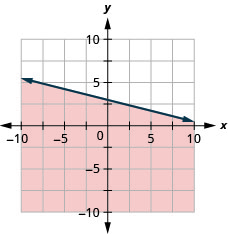
96. رسم بياني للتفاوت الخطي$x−y\leq 5$.

97. رسم بياني للتفاوت الخطي$3x+2y>10.$

إجابة

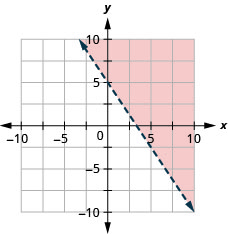
98. رسم بياني للتفاوت الخطي$y\leq −3x$.

99. رسم بياني للتفاوت الخطي$y<6.$

إجابة

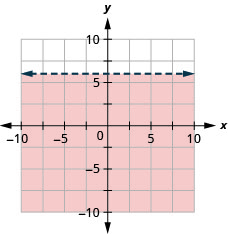
حل التطبيقات باستخدام المتباينات الخطية في متغيرين

100. تحتاج Shanthie إلى كسب 500 دولار على الأقل أسبوعيًا خلال إجازتها الصيفية لدفع تكاليف الكلية. إنها تعمل بوظيفتين. أحدهما كمدرب سباحة يدفع 10 دولارات في الساعة والآخر كمتدرب في مكتب محاماة مقابل 25 دولارًا في الساعة. كم عدد الساعات التي تحتاجها Shanthie للعمل في كل وظيفة لكسب 500 دولار على الأقل في الأسبوع؟

ⓐ اجعل x هو عدد الساعات التي تعمل فيها في تعليم السباحة وليكن عدد الساعات التي تعمل فيها كمتدربة. اكتب عدم المساواة التي من شأنها أن تمثل هذا الموقف.
ⓑ رسم بياني لعدم المساواة.
ⓒ ابحث عن ثلاثة أزواج مرتبة من$(x,y)$ شأنها أن تكون حلولًا لعدم المساواة. ثم اشرح ماذا يعني ذلك لشانثي.

101. أتسوشي يحتاج إلى ممارسة ما يكفي لحرق$600$ السعرات الحرارية كل يوم. إنه يفضل الركض أو ركوب الدراجة وحرق$20$ السعرات الحرارية في الدقيقة أثناء الجري$15$ والسعرات الحرارية في الدقيقة أثناء ركوب الدراجات.

ⓐ إذا كان x هو عدد الدقائق التي يركضها أتسوشي و y هو عدد الدقائق التي يدرجها، فأوجد عدم المساواة التي تمثل الموقف.
ⓑ رسم بياني لعدم المساواة.
ⓒ ضع قائمة بثلاثة حلول لعدم المساواة. ما الخيارات التي توفرها الحلول لـ Atsushi؟

إجابة

ⓐ$20x+15y\geq 60020x+15y\geq 600$
ⓑ

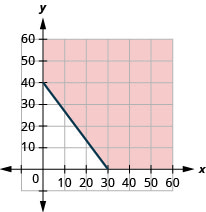
ⓒ ستختلف الإجابات.

العلاقات والوظائف

ابحث عن مجال ونطاق العلاقة

في التمارين التالية، لكل علاقة، ⓐ ابحث عن مجال العلاقة ⓑ ابحث عن نطاق العلاقة.

102. ${\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}$

103. ${\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}$

إجابة

ⓐ$D: {−3, −2, −1, 0}$
ⓑ$R: {7, 3, 9, −3, 8}$

في التمرين التالي، استخدم تخطيط العلاقة بـ ⓐ ضع قائمة بالأزواج المرتبة للعلاقة ⓑ ابحث عن مجال العلاقة ⓒ ابحث عن نطاق العلاقة.

104. يوضح الرسم البياني أدناه متوسط وزن الطفل وفقًا للعمر.

في التمرين التالي، استخدم الرسم البياني للعلاقة بـ ⓐ ضع قائمة بالأزواج المرتبة للعلاقة ⓑ ابحث عن مجال العلاقة ⓒ ابحث عن نطاق العلاقة.

105.

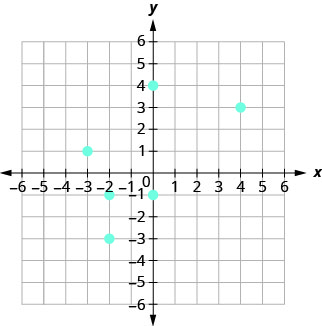
إجابة

ⓐ$(4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)$
ⓑ$D: {−3, −2, 0, 4}$
ⓒ$R: {−3, −1, 1, 3, 4}$

حدد ما إذا كانت العلاقة دالة

في التمارين التالية، استخدم مجموعة الأزواج المرتبة ⓐ لتحديد ما إذا كانت العلاقة دالة ⓑ ابحث عن مجال العلاقة ⓒ ابحث عن نطاق العلاقة.

106. ${\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}$

107. ${\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}$

إجابة

ⓐ نعم ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${0, 1, 8, 27}$

في التمارين التالية، استخدم التخطيط ⓐ لتحديد ما إذا كانت العلاقة دالة ⓑ ابحث عن مجال الدالة ⓒ ابحث عن نطاق الدالة.

108.

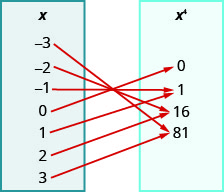
109.

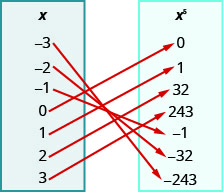
إجابة

ⓐ${−3, −2, −1, 0, 1, 2, 3}$
ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${−243, −32, −1, 0, 1, 32, 243}$

في التمارين التالية، حدد ما إذا كانت كل معادلة دالة.

110. $2x+y=−3$

111. $y=x^2$

إجابة

نعم

112. $y=3x−5$

113. $y=x^3$

إجابة

نعم

114. $2x+y2=4$

أوجد قيمة الدالة

في التمارين التالية، قم بتقييم الوظيفة:

ⓐ$f(−2)$ ⓑ$f(3)$ ⓒ$f(a)$.

115. $f(x)=3x−4$

إجابة

ⓐ$f(−2)=−10$ ⓑ$f(3)=5$ ⓒ$f(a)=3a−4$

116. $f(x)=−2x+5$

117. $f(x)=x^2−5x+6$

إجابة

ⓐ$f(−2)=20$ ⓑ$f(3)=0$ ⓒ$f(a)=a^2−5a+6$

118. $f(x)=3x^2−2x+1$

في التمارين التالية، قم بتقييم الوظيفة.

119. $g(x)=3x2−5x;\space g(2)$

إجابة

$2$

120. $F(x)=2x2−3x+1;\space F(−1)$

121. $h(t)=4|t−1|+2;\space h(t)=4$

إجابة

$18$

122. $f(x)=x+2x−1;\space f(3)$

رسوم بيانية للدوال

استخدم اختبار الخط العمودي

في التمارين التالية، حدد ما إذا كان كل رسم بياني يمثل رسمًا بيانيًا لدالة.

123.

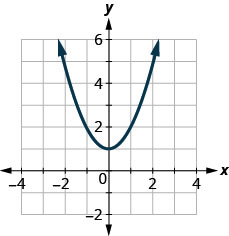
إجابة

نعم

124.

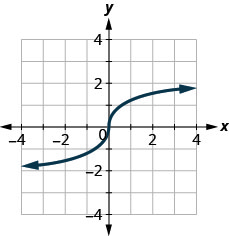
125.

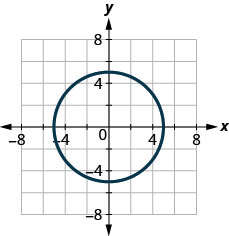
إجابة

كلا

126.

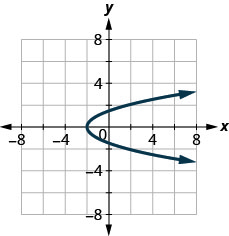
127.

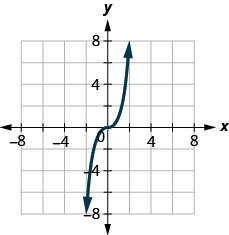
إجابة

نعم

128.

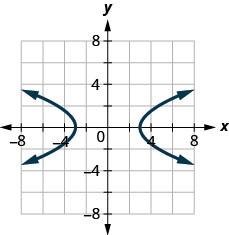
129.

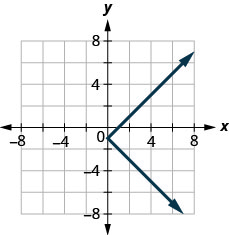
إجابة

كلا

تحديد الرسوم البيانية للوظائف الأساسية

في التمارين التالية، ⓐ رسم بياني لكل دالة ⓑ حدد نطاقها ونطاقها. اكتب المجال والنطاق في الترميز الفاصل الزمني.

130. $f(x)=5x+1$

131. $f(x)=−4x−2$

إجابة

ⓐ

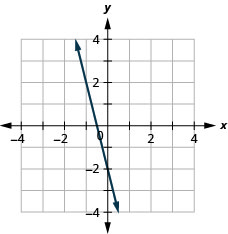
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

132. $f(x)=\frac{2}{3}x−1$

133. $f(x)=−6$

إجابة

ⓐ

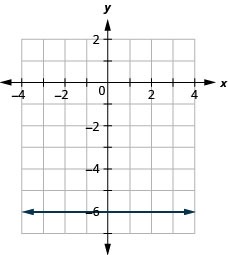
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

134. $f(x)=2x$

135. $f(x)=3x^2$

إجابة

ⓐ

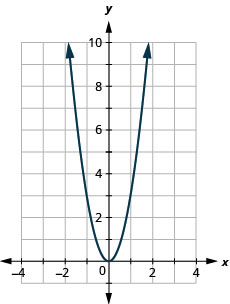
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,0]$

136. $f(x)=−12x^2$

137. $f(x)=x^2+2$

إجابة

ⓐ

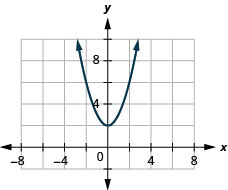
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

138. $f(x)=x^3−2$

139. $f(x)=\sqrt{x+2}$

إجابة

ⓐ

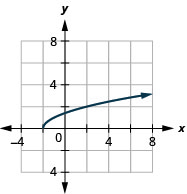
ⓑ$D: [−2,−2, \inf ), \space R: [0,\inf )$

140. $f(x)=−|x|$

141. $f(x)=|x|+1$

إجابة

ⓐ

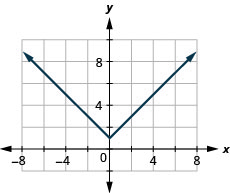
ⓑ$D: (-\inf ,\inf ), \space R: [1,\inf )$

اقرأ المعلومات من الرسم البياني للدالة

في التمارين التالية، استخدم الرسم البياني للدالة للعثور على مجالها ونطاقها. اكتب المجال والنطاق في الترميز الفاصل الزمني

142.

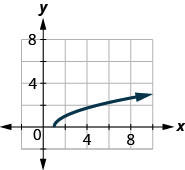
143.

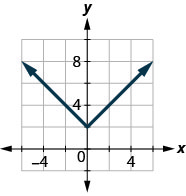
إجابة

$D: (-\inf ,\inf ), R: [2,\inf )$

144.

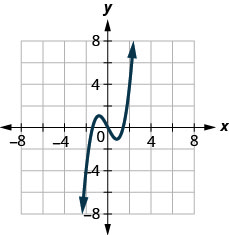
في التمارين التالية، استخدم الرسم البياني للدالة للعثور على القيم المشار إليها.

145.

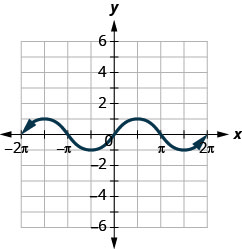
ⓐ ابحث$f(0)$.
ⓑ ابحث$f(12\pi )$.
ⓒ ابحث$f(−32\pi )$.
ⓓ ابحث عن القيم الخاصة$x$ بالوقت$f(x)=0$.
ⓔ ابحث عن$x$ -Intercepts.
ⓕ ابحث عن$y$ التقاطع (التقاطعات).
ⓖ ابحث عن المجال. اكتبها في تدوين الفاصل الزمني.
ⓗ ابحث عن النطاق. اكتبها في تدوين الفاصل الزمني.

إجابة

ⓐ$f(x)=0$ ⓑ$f(\pi /2)=1$
ⓒ$f(−3\pi /2)=1$ ⓓ$f(x)=0$ لـ$x=−2\pi ,−\pi ,0,\pi ,2\pi$
ⓔ$(−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)$ ⓕ$(0,0)$
ⓖ$[−2\pi ,2\pi ]$ ⓗ$[−1,1]$

146.

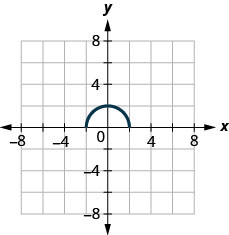
ⓐ ابحث$f(0)$.
ⓑ ابحث عن القيم الخاصة$x$ بالوقت$f(x)=0$.
ⓒ ابحث عن$x$ -Intercepts.
ⓓ ابحث عن$y$ التقاطع (التقاطعات).
ⓔ ابحث عن المجال. اكتبها في تدوين الفاصل الزمني.
ⓕ ابحث عن النطاق. اكتبها في تدوين الفاصل الزمني.

اختبار الممارسة

1. ارسم كل نقطة في نظام إحداثيات مستطيل.

ⓐ$(2,5)$
ⓑ$(−1,−3)$
ⓒ$(0,2)$
ⓓ$(−4,32)$
ⓔ$(5,0)$

إجابة

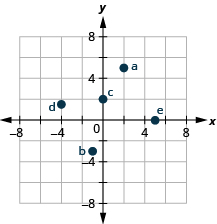
2. أي من الأزواج المرتبة المعطاة تمثل حلولًا للمعادلة$3x−y=6$؟

ⓐ$(3,3)$ ⓑ$(2,0)$ ⓒ$(4,−6)$

3. أوجد ميل كل خط موضَّح.

ⓐ

ⓑ

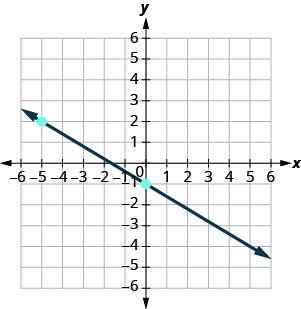
إجابة

ⓐ$−\frac{3}{5}$ ⓑ غير محدد

4. أوجد ميل الخط الفاصل بين النقطتين$(5,2)$ و$(−1,−4)$.

5. ارسم بيانيًا الخط الذي$\frac{1}{2}$ يحتوي على المنحدر الذي يحتوي على النقطة$(−3,−4)$.

إجابة

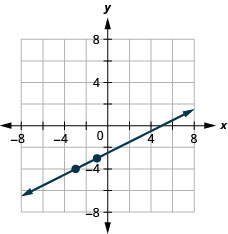
6. ابحث عن الأجزاء المقطوعة$4x+2y=−8$ والرسم البياني.

ارسم خطًا لكل من المعادلات التالية.

7. $y=\frac{5}{3}x−1$

إجابة

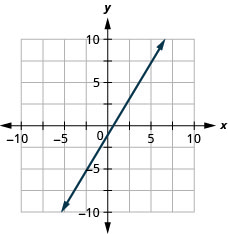
8. $y=−x$

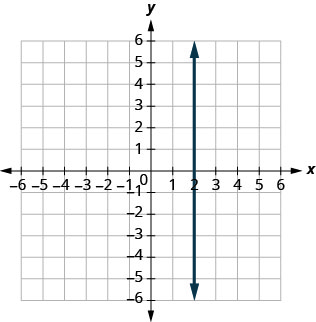
9. $y=2$

إجابة

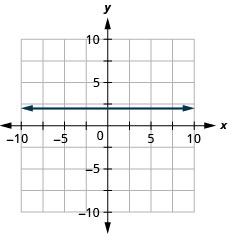
أوجد معادلة كل سطر. اكتب المعادلة في صورة تقاطع منحدر.

10. المنحدر$−\frac{3}{4}$$y$ والاعتراض$(0,−2)$

11. $m=2$، نقطة$(−3,−1)$

إجابة

$y=2x+5$

12. تحتوي على$(10,1)$ و$(6,−1)$

13. عمودي على الخط$y=\frac{5}{4}x+2$، يحتوي على النقطة$(−10,3)$

إجابة

$y=−\frac{4}{5}x−5$

14. اكتب عدم المساواة التي يوضحها الرسم البياني مع خط الحدود$y=−x−3$.

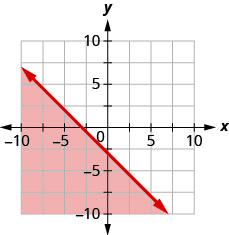
ارسم بيانيًا لكل عدم مساواة خطية.

15. $y>\frac{3}{2}x+5$

إجابة

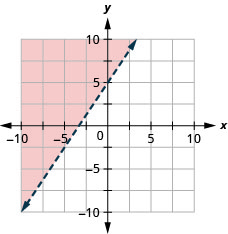
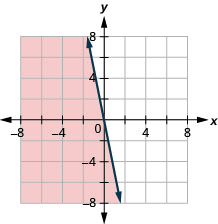
16. $x−y\geq −4$

17. $y\leq −5x$

إجابة

18. تعمل هيرو في وظيفتين بدوام جزئي من أجل كسب ما يكفي من المال للوفاء بالتزاماتها بما لا يقل عن 450 دولارًا في الأسبوع. تدفع وظيفتها في المركز التجاري 10 دولارات في الساعة وتدفع وظيفتها المساعدة الإدارية في الحرم الجامعي 15 دولارًا في الساعة. كم عدد الساعات التي يحتاجها هيرو للعمل في كل وظيفة لكسب 450 دولارًا على الأقل؟

ⓐ ليكن x عدد ساعات عملها في المركز التجاري وليكن y هو عدد الساعات التي تعمل فيها كمساعد إداري. اكتب عدم المساواة التي من شأنها أن تمثل هذا الموقف.
ⓑ رسم بياني لعدم المساواة.
ⓒ ابحث عن ثلاثة أزواج مرتبة من$(x,y)$ شأنها أن تكون حلولًا لعدم المساواة. ثم اشرح ما يعنيه ذلك لهيرو.

19. استخدم مجموعة الأزواج المرتبة ⓐ لتحديد ما إذا كانت العلاقة دالة أم لا، ⓑ ابحث عن مجال العلاقة، و ⓒ للعثور على نطاق العلاقة.

\ ({\ {(−3,27)، (−2,8)، (−1,1)، (0,0)،
(1,1)، (2,8)، (3,27)}\}\)

إجابة

ⓐ نعم ⓑ${\{−3,−2,−1,0,1,2,3}\}$ ⓒ${\{0, 1, 8, 27}\}$

20. قم بتقييم الوظيفة: ⓐ$f(−1)$ ⓑ$f(2)$ ⓒ$f(c)$.

$f(x)=4x^2−2x−3$

21. من$h(y)=3|y−1|−3$ أجل التقييم$h(−4)$.

إجابة

$12$

22. حدِّد ما إذا كان الرسم البياني هو الرسم البياني للدالة. اشرح إجابتك.

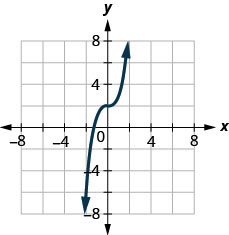
في التمارين التالية، ⓐ رسم بياني لكل دالة ⓑ حدد نطاقها ونطاقها.
اكتب المجال والنطاق في الترميز الفاصل الزمني.

23. $f(x)=x^2+1$

إجابة

ⓐ

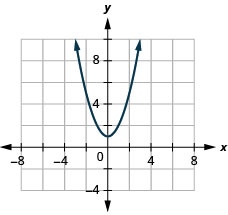
ⓑ$D: (-\inf ,\inf ), R: [1,\inf )$

24. $f(x)=\sqrt{x+1}$

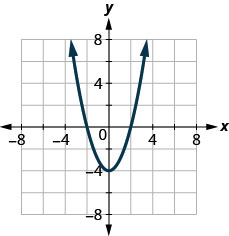
ⓑ ابحث عن$y$ -Intercepts.
ⓒ ابحث$f(−1)$.
ⓓ ابحث$f(1)$.
ⓔ ابحث عن المجال. اكتبها في تدوين الفاصل الزمني.
ⓕ ابحث عن النطاق. اكتبها في تدوين الفاصل الزمني.

إجابة

ⓐ$x=−2,2$ ⓑ$y=−4$
ⓒ$f(−1)=−3$ ⓓ$f(1)=−3$
ⓔ$D: (-\inf ,\inf )$ ⓕ$R: [−4, \inf)$