3.6: العلاقات والوظائف

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• ابحث عن مجال ونطاق العلاقة
• حدد ما إذا كانت العلاقة دالة
• ابحث عن قيمة الدالة

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. قم بتقييم$3x−5$ متى$x=−2$.
   إذا فاتتك هذه المشكلة، راجع [link].
2. قم بتقييم$2x^2−x−3$ متى$x=a$.
   إذا فاتتك هذه المشكلة، راجع [link].
3. قم بالتبسيط:$7x−1−4x+5$.
   إذا فاتتك هذه المشكلة، راجع [link].

ابحث عن مجال ونطاق العلاقة

بينما نمضي في حياتنا اليومية، لدينا العديد من عناصر البيانات أو الكميات المقترنة بأسمائنا. يتم مطابقة رقم الضمان الاجتماعي ورقم هوية الطالب وعنوان البريد الإلكتروني ورقم الهاتف وعيد ميلادنا مع اسمنا. هناك علاقة بين اسمنا وكل عنصر من هذه العناصر.

عندما تحصل أستاذتك على قائمة الفصل الخاصة بها، يتم سرد أسماء جميع الطلاب في الفصل في عمود واحد ومن ثم من المحتمل أن يكون رقم معرف الطالب في العمود التالي. إذا فكرنا في المراسلات كمجموعة من الأزواج المرتبة، حيث يكون العنصر الأول هو اسم الطالب والعنصر الثاني هو رقم هوية الطالب، فإننا نسمي هذه العلاقة.

$$(\text{Student name}, \text{ Student ID #})\nonumber$$

يُطلق على مجموعة جميع أسماء الطلاب في الفصل اسم مجال العلاقة ومجموعة جميع أرقام معرف الطالب المقترنة بهؤلاء الطلاب هي نطاق العلاقة.

هناك العديد من الحالات المشابهة التي يتم فيها اقتران متغير واحد أو مطابقته مع متغير آخر. مجموعة الأزواج المرتبة التي تسجل هذه المطابقة هي علاقة.

التعريف: العلاقة

العلاقة هي أي مجموعة من الأزواج المرتبة$(x,y)$. تشكل جميع قيم x في الأزواج المرتبة معًا المجال. تشكل جميع قيم y في الأزواج المرتبة معًا النطاق.

مثال$\PageIndex{1}$

بالنسبة للعلاقة${(1,1),(2,4),(3,9),(4,16),(5,25)}$:

1. ابحث عن مجال العلاقة.
2. ابحث عن نطاق العلاقة.

إجابة

$$\begin{array} {ll} {} &{ {\{(1,1), (2,4), (3,9), (4,16), (5,25) }\} } \\ {ⓐ\text{ The domain is the set of all x-values of the relation.}} &{ {\{1,2,3,4,5}\} } \\ {ⓑ\text{ The range is the set of all y-values of the relation.}} &{ {\{1,4,9,16,25}\} } \\ \nonumber \end{array}$$

مثال$\PageIndex{2}$

بالنسبة للعلاقة${\{(1,1),(2,8),(3,27),(4,64),(5,125)}\}$:

1. ابحث عن مجال العلاقة.
2. ابحث عن نطاق العلاقة.

الإجابة أ

${\{1,2,3,4,5}\}$

الإجابة ب

${\{1,8,27,64,125}\}$

مثال$\PageIndex{3}$

بالنسبة للعلاقة${\{(1,3),(2,6),(3,9),(4,12),(5,15)}\}$:

1. ابحث عن مجال العلاقة.
2. ابحث عن نطاق العلاقة.

الإجابة أ

${\{1,2,3,4,5}\}$

الإجابة ب

${\{3,6,9,12,15}\}$

رسم الخرائط

يُستخدم التخطيط أحيانًا لإظهار العلاقة. تعرض الأسهم الاقتران بين عناصر المجال وعناصر النطاق.

مثال$\PageIndex{4}$

استخدم تخطيط العلاقة الموضحة لـ

1. ضع قائمة بالأزواج المرتبة للعلاقة،
2. ابحث عن مجال العلاقة، و
3. ابحث عن نطاق العلاقة.

إجابة

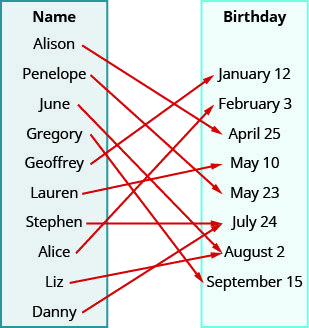
ⓐ يُظهر السهم مطابقة الشخص لعيد ميلاده. نقوم بإنشاء أزواج مرتبة باستخدام اسم الشخص كقيمة x وتاريخ ميلاده كقيمة y.

{(أليسون، 25 أبريل)، (بينيلوب، 23 مايو)، (يونيو، 2 أغسطس)، (غريغوري، 15 سبتمبر)، (جيفري، 12 يناير)، (لورين، 10 مايو)، (ستيفن، 24 يوليو)، (أليس، 3 فبراير)، (ليز، 2 أغسطس)، (داني، 24 يوليو)}

ⓑ المجال هو مجموعة جميع قيم x للعلاقة.

{أليسون، بينيلوب، جون، غريغوري، جيفري، لورين، ستيفن، أليس، ليز، داني}

ⓒ النطاق هو مجموعة جميع قيم y للعلاقة.

{12 يناير، 3 فبراير، 25 أبريل، 10 مايو، 23 مايو، 24 يوليو، 2 أغسطس، 15 سبتمبر}

مثال$\PageIndex{5}$

استخدم تخطيط العلاقة الموضحة لـ

1. ضع قائمة بالأزواج المرتبة للعلاقة
2. ابحث عن مجال العلاقة
3. ابحث عن نطاق العلاقة.

إجابة

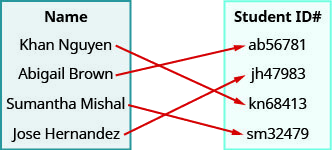
ⓐ (خان نغوين، kn68413)، (أبيجيل براون، ab56781)، (سومانثا ميشال، sm32479)، (خوسيه هيرن وإيز، jh47983)

ⓑ {خان نغوين، أبيجيل براون، سومانثا ميشال، خوسيه هيرن وإيز}

ⓒ {kn68413، ab56781، sm32479، jh47983}

مثال$\PageIndex{6}$

استخدم تخطيط العلاقة الموضحة لـ

1. ضع قائمة بالأزواج المرتبة للعلاقة
2. ابحث عن مجال العلاقة
3. ابحث عن نطاق العلاقة.

إجابة

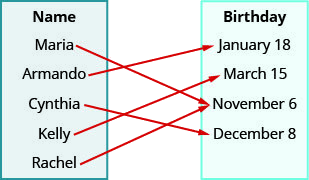
ⓐ (ماريا، 6 نوفمبر)، (أرم أند كو، 18 يناير)، (سينثيا، 8 ديسمبر)، (كيلي، 15 مارس)، (راشيل، 6 نوفمبر)

ⓑ {ماريا، أرمي أند أو، سينثيا، كيلي، راشيل}

ⓒ {6 نوفمبر، 18 يناير، 8 ديسمبر، 15 مارس}

الرسم البياني هو طريقة أخرى يمكن من خلالها تمثيل العلاقة. مجموعة الأزواج المرتبة لجميع النقاط المرسومة هي العلاقة. مجموعة جميع إحداثيات x هي مجال العلاقة ومجموعة جميع إحداثيات y هي النطاق. بشكل عام نكتب الأرقام بترتيب تصاعدي لكل من المجال والنطاق.

مثال$\PageIndex{7}$

استخدم الرسم البياني للعلاقة بـ

1. ضع قائمة بالأزواج المرتبة للعلاقة
2. ابحث عن مجال العلاقة
3. ابحث عن نطاق العلاقة.

إجابة

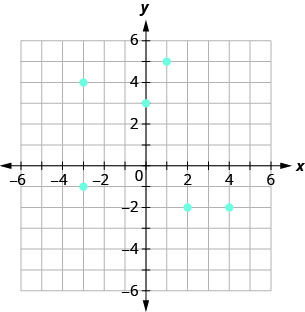
ⓐ الأزواج المرتبة للعلاقة هي: $${\{(1,5),(−3,−1),(4,−2),(0,3),(2,−2),(−3,4)}\}.\nonumber$$

ⓑ المجال هو مجموعة جميع قيم x للعلاقة:$\quad {\{−3,0,1,2,4}\}$.

لاحظ أنه أثناء$−3$ التكرار، يتم إدراجه مرة واحدة فقط.

ⓒ النطاق هو مجموعة جميع قيم y للعلاقة:$\quad {\{−2,−1,3,4,5}\}$.

لاحظ أنه أثناء$−2$ التكرار، يتم إدراجه مرة واحدة فقط.

مثال$\PageIndex{8}$

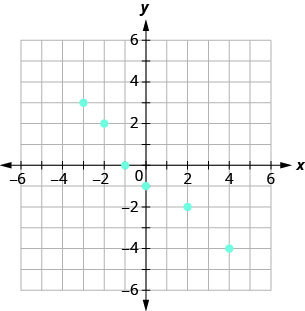
استخدم الرسم البياني للعلاقة بـ

1. ضع قائمة بالأزواج المرتبة للعلاقة
2. ابحث عن مجال العلاقة
3. ابحث عن نطاق العلاقة.
4. 

إجابة

ⓐ$(−3,3),(−2,2),(−1,0),$
$(0,−1),(2,−2),(4,−4)$
ⓑ${\{−3,−2,−1,0,2,4}\}$
ⓒ${\{3,2,0,−1,−2,−4}\}$

مثال$\PageIndex{9}$

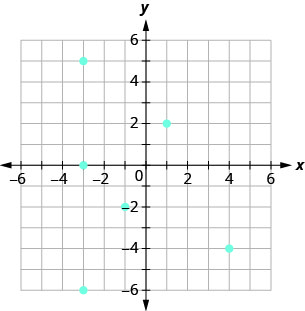
استخدم الرسم البياني للعلاقة بـ

1. ضع قائمة بالأزواج المرتبة للعلاقة
2. ابحث عن مجال العلاقة
3. ابحث عن نطاق العلاقة.

إجابة

ⓐ$(−3,0),(−3,5),(−3,−6),$
$(−1,−2),(1,2),(4,−4)$
ⓑ${\{−3,−1,1,4}\}$
ⓒ${\{−6,0,5,−2,2,−4}\}$

حدد ما إذا كانت العلاقة دالة

يحدث نوع خاص من العلاقات، يسمى الدالة، على نطاق واسع في الرياضيات. الدالة هي علاقة تخصص لكل عنصر في مجاله عنصرًا واحدًا بالضبط في النطاق. بالنسبة لكل زوج مرتب في العلاقة، تتم مطابقة كل قيمة x بقيمة y واحدة فقط.

التعريف: الوظيفة

الدالة هي علاقة تخصص لكل عنصر في مجاله عنصرًا واحدًا بالضبط في النطاق.

يساعدنا مثال عيد الميلاد من Example على فهم هذا التعريف. كل شخص لديه عيد ميلاد ولكن لا أحد لديه عيد ميلاد. لا بأس أن يشارك شخصان عيد ميلاد. لا بأس أن يشارك داني وستيفن يوم 24 ^يوليو عيد ميلادهما وأن يشارك يونيو وليز يوم 2 ^أغسطس. نظرًا لأن كل شخص لديه تاريخ ميلاد واحد بالضبط، فإن العلاقة في المثال هي وظيفة.

تتضمن العلاقة التي يظهرها الرسم البياني في المثال الأزواج المرتبة$(−3,−1)$ و$(−3,4)$. هل هذا مقبول في الوظيفة؟ لا، لأن هذا مثل شخص واحد لديه عيد ميلاد مختلفين.

مثال$\PageIndex{10}$

استخدم مجموعة الأزواج المرتبة لـ (i) تحديد ما إذا كانت العلاقة دالة (ii) للعثور على مجال العلاقة (iii) للعثور على نطاق العلاقة.

1. ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$
2. ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

إجابة

ⓐ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$

(i) تتم مطابقة كل قيمة x بقيمة y واحدة فقط. لذا فإن هذه العلاقة هي دالة.

(ii) المجال هو مجموعة جميع قيم x في العلاقة.
المجال هو:${\{−3,−2,−1,0,1,2,3}\}$.

(iiii) النطاق هو مجموعة جميع قيم y في العلاقة. لاحظ أننا لا ندرج قيم النطاق مرتين.
النطاق هو:${\{27,8,1,0}\}$.

ⓑ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

(i) تتم مطابقة القيمة x -value 9 بقيمتين y، كل من 3 و$−3$. لذا فإن هذه العلاقة ليست دالة.

(ii) المجال هو مجموعة جميع قيم x في العلاقة. لاحظ أننا لا ندرج قيم النطاق مرتين.
المجال هو:${\{0,1,2,4,9}\}$.

(iiii) النطاق هو مجموعة جميع قيم y في العلاقة.
النطاق هو:${\{−3,−2,−1,0,1,2,3}\}$.

مثال$\PageIndex{11}$

استخدم مجموعة الأزواج المرتبة لـ (i) تحديد ما إذا كانت العلاقة دالة (ii) للعثور على مجال العلاقة (iii) للعثور على نطاق الدالة.

1. ${\{(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}\}$
2. ${\{(8,−4),(4,−2),(2,−1),(0,0),(2,1),(4,2),(8,4)}\}$

إجابة

ⓐ نعم؛${\{−3,−2,−1,0,1,2,3}\}$؛
${\{−6,−4,−2,0,2,4,6}\}$
ⓑ لا${\{0,2,4,8}\}$؛
${\{−4,−2,−1,0,1,2,4}\}$

مثال$\PageIndex{12}$

استخدم مجموعة الأزواج المرتبة لـ (i) تحديد ما إذا كانت العلاقة دالة (ii) للعثور على مجال العلاقة (iii) للعثور على نطاق العلاقة.

1. ${\{(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}\}$
2. ${\{(7,−3),(−5,−4),(8,−0),(0,0),(−6,4),(−2,2),(−1,3)}\}$

إجابة

ⓐ لا؛${\{0,1,8,27}\}$؛
${\{−3,−2,−1,0,2,2,3}\}$
ⓑ نعم${\{7,−5,8,0,−6,−2,−1}\}$؛
${\{−3,−4,0,4,2,3}\}$

مثال$\PageIndex{13}$

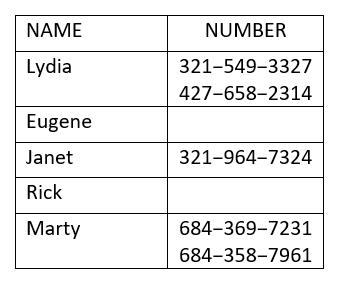
استخدم التخطيط لـ

1. تحديد ما إذا كانت العلاقة دالة
2. ابحث عن مجال العلاقة
3. ابحث عن نطاق العلاقة.

إجابة

ⓐ لدى كل من ليديا ومارتي رقمي هاتف. لذلك لا تتم مطابقة كل قيمة x مع قيمة y -value واحدة فقط. لذا فإن هذه العلاقة ليست دالة.

ⓑ المجال هو مجموعة جميع قيم x في العلاقة. النطاق هو: {ليديا، يوجين، جانيت، ريك، مارتي}

ⓒ النطاق هو مجموعة جميع قيم y في العلاقة. النطاق هو:

${\{321-549-3327, 427-658-2314, 321-964-7324, 684-358-7961, 684-369-7231, 798-367-8541}\}$

مثال$\PageIndex{14}$

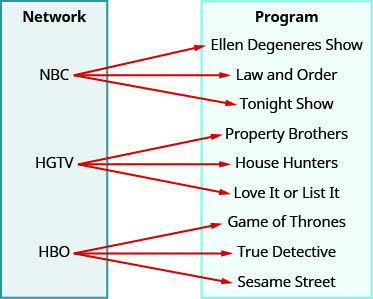
استخدم التعيين ⓐ لتحديد ما إذا كانت العلاقة دالة ⓑ ابحث عن مجال العلاقة ⓒ ابحث عن نطاق العلاقة.

إجابة

ⓐ لا ⓑ {إن بي سي، إتش جي تي في، إتش بي أو} ⓒ {إلين ديجينيرز شو، لو آند أوردر، تونايت شو، بروبيرتي براذرز، هاوس هانترز، أحبوها أو أطلقوها على القائمة، غيم أوف ثرونز، المحقق الحقيقي، شارع سمسم

مثال$\PageIndex{15}$

استخدم التخطيط لـ

1. تحديد ما إذا كانت العلاقة دالة
2. ابحث عن مجال العلاقة
3. ابحث عن نطاق العلاقة.

 

إجابة

ⓐ لا ⓑ {نيل، كريستال، كيلفن، جورج، كريستا، مايك} ⓒ {123-567-4839 عمل، 231-378-5941 خلية، 743-469-9731 خلية، 567-534-2970 عمل، 684-369-7231 خلية، 798-367-8541 خلية، 639-847-6971 خلية}

في الجبر، في أغلب الأحيان، سيتم تمثيل الوظائف بمعادلة. من الأسهل معرفة ما إذا كانت المعادلة دالة عندما يتم حلها لـ y. إذا كانت كل قيمة من قيم x تؤدي إلى قيمة واحدة فقط لـ y، فإن المعادلة تحدد الدالة.

مثال$\PageIndex{16}$

حدد ما إذا كانت كل معادلة دالة.

1. $2x+y=7$
2. $y=x^2+1$
3. $x+y^2=3$

إجابة

ⓐ$2x+y=7$

لكل قيمة x، نضربها$−2$ ثم نضيف 7 للحصول على القيمة y

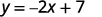
على سبيل المثال، إذا$x=3$: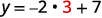

لدينا ذلك عندما$x=3$، إذن$y=1$. ستعمل بشكل مشابه لأي قيمة x. نظرًا لأن كل قيمة من قيم x، تتوافق مع قيمة واحدة فقط من y، فإن المعادلة تحدد الدالة.

ⓑ$y=x^2+1$

لكل قيمة x، نقوم بترتيبها ثم نضيف 1 للحصول على القيمة y.

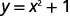
على سبيل المثال، إذا$x=2$:

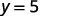
لدينا ذلك عندما$x=2$، إذن$y=5$. ستعمل بشكل مشابه لأي قيمة x. نظرًا لأن كل قيمة من قيم x، تتوافق مع قيمة واحدة فقط من y، فإن المعادلة تحدد الدالة.

ⓒ

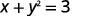
اعزل مصطلح y.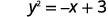
دعونا نستبدل$x=2$.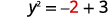
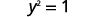
هذا يعطينا قيمتين لـ y.	$y=1\space y=−1$

لقد أظهرنا$x=2$ ذلك متى ثم$y=1$ و$y=−1$. ستعمل بشكل مشابه لأي قيمة x. نظرًا لأن كل قيمة لـ x لا تتوافق مع قيمة واحدة فقط لـ y، فإن المعادلة لا تحدد دالة.

مثال$\PageIndex{17}$

حدد ما إذا كانت كل معادلة دالة.

1. $4x+y=−3$
2. $x+y^2=1$
3. $y−x^2=2$

إجابة

ⓐ نعم ⓑ لا ⓒ نعم

مثال$\PageIndex{18}$

حدد ما إذا كانت كل معادلة دالة.

1. $x+y^2=4$
2. $y=x^2−7$
3. $y=5x−4$

إجابة

ⓐ لا ⓑ نعم ⓒ نعم

أوجد قيمة الدالة

من الملائم جدًا تسمية دالة وغالبًا ما نسميها f أو g أو h أو F أو G أو H. في أي وظيفة، لكل قيمة x من المجال نحصل على قيمة y المقابلة في النطاق. بالنسبة للدالة$f$، نكتب قيمة النطاق هذه$y$ كـ$f(x)$. وهذا ما يسمى بتدوين الدالة ويتم قراءته$f$$x$ أو قيمة$f$ at$x$. في هذه الحالة، لا تشير الأقواس إلى الضرب.

التعريف: تدوين الدالة

للحصول على الوظيفة$y=f(x)$

$$\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}$$

نقرأ$f(x)$ اعتبارًا$f$ من$x$ أو قيمة$f$ at$x$.

نسمي x المتغير المستقل لأنه يمكن أن يكون أي قيمة في المجال. نسمي y المتغير التابع حيث تعتمد قيمته على x.

المتغيرات المستقلة والتابعة

بالنسبة للوظيفة$y=f(x)$،

$$\begin{array} {l} {x \text{ is the independent variable as it can be any value in the domain}} \\ {y \text{ the dependent variable as its value depends on } x} \\ \nonumber \end{array}$$

كما هو الحال عندما واجهت المتغير x لأول مرة، قد يكون تدوين الدالة مزعجًا إلى حد ما. يبدو غريبًا لأنه جديد. ستشعر براحة أكبر مع الترميز أثناء استخدامه.

دعونا ننظر إلى المعادلة$y=4x−5$. لإيجاد قيمة y عندما$x=2$، نعلم أنه يجب استبدال$x=2$ المعادلة ثم تبسيطها.

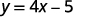دع x=2.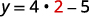

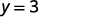قيمة الدالة at$x=2$ هي 3.

نحن نفعل نفس الشيء باستخدام الترميز الوظيفي،$y=4x−5$ يمكن كتابة المعادلة كـ$f(x)=4x−5$. للعثور على القيمة عندما$x=2$ نكتب:

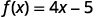دع x=2.

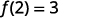قيمة الدالة at$x=2$ هي 3.

تسمى عملية العثور على قيمة قيمة معينة$f(x)$ لـ x بتقييم الدالة.

مثال$\PageIndex{19}$

بالنسبة للوظيفة$f(x)=2x^2+3x−1$، قم بتقييم الدالة.

1. $f(3)$
2. $f(−2)$
3. $f(a)$

إجابة

ⓐ

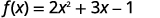
للتقييم$f(3)$، استبدل 3 بـ x.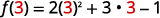
قم بالتبسيط.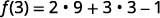

ⓑ

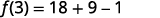
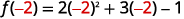
قم بالتبسيط.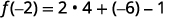

ⓒ

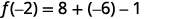
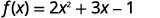
لتقييم f (أ) و (و) (أ)، يستعاض عن x بـ x.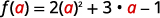
قم بالتبسيط.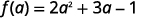

مثال$\PageIndex{20}$

بالنسبة للوظيفة$f(x)=3x^2−2x+1$، قم بتقييم الدالة.

1. $f(3)$
2. $f(−1)$
3. $f(t)$

إجابة

ⓐ$f(3)=22$ ⓑ$f(−1)=6$ ⓒ$f(t)=3t^2−2t−1$

مثال$\PageIndex{21}$

بالنسبة للوظيفة$f(x)=2x^2+4x−3$، قم بتقييم الدالة.

1. $f(2)$
2. $f(−3)$
3. $f(h)$

إجابة

ⓐ$(2)=13$ ⓑ$f(−3)=3$
ⓒ$f(h)=2h2+4h−3$

في المثال الأخير، وجدنا قيمة ثابتة$f(x)$ لـ x. في المثال التالي، يُطلب منا العثور$g(x)$ على قيم x التي تمثل متغيرات. ما زلنا نتبع نفس الإجراء ونستبدل المتغيرات بـ x.

مثال$\PageIndex{22}$

بالنسبة للوظيفة$g(x)=3x−5$، قم بتقييم الدالة.

1. $g(h^2)$
2. $g(x+2)$
3. $g(x)+g(2)$

إجابة

ⓐ

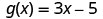
للتقييم$g(h^2)$، استبدل$h^2$ x.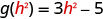

ⓑ

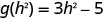
للتقييم$g(x+2)$، استبدل$x+2$ x.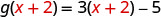
قم بالتبسيط.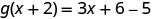

ⓒ

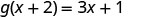
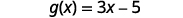
للتقييم$g(x)+g(2)$، ابحث أولاً$g(2)$.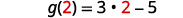
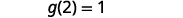
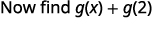
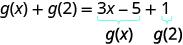
قم بالتبسيط.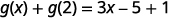

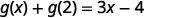
لاحظ الفرق بين الجزء ⓑ و ⓒ. نحصل على$g(x+2)=3x+1$ و$g(x)+g(2)=3x−4$. لذلك نرى ذلك$g(x+2)\neq g(x)+g(2)$.

مثال$\PageIndex{23}$

بالنسبة للوظيفة$g(x)=4x−7$، قم بتقييم الدالة.

1. $g(m^2)$
2. $g(x−3)$
3. $g(x)−g(3)$

إجابة

ⓐ$4m^2−7$ ⓑ$4x−19$
ⓒ$x−12$

مثال$\PageIndex{24}$

بالنسبة للوظيفة$h(x)=2x+1$، قم بتقييم الدالة.

1. $h(k^2)$
2. $h(x+1)$
3. $h(x)+h(1)$

إجابة

ⓐ$2k^2+1$ ⓑ$2x+3$
ⓒ$2x+4$

يمكن تصميم العديد من المواقف اليومية باستخدام الوظائف.

مثال$\PageIndex{25}$

عدد رسائل البريد الإلكتروني غير المقروءة في حساب سيلفيا هو 75. يزداد هذا الرقم بمقدار 10 رسائل بريد إلكتروني غير مقروءة يوميًا. $N(t)=75+10t$تمثل الدالة العلاقة بين عدد رسائل البريد الإلكتروني، N، والوقت، t، المقاسة بالأيام.

1. حدد المتغير المستقل والمعتمد.
2. ابحث$N(5)$. اشرح ما تعنيه هذه النتيجة.

إجابة

ⓐ عدد رسائل البريد الإلكتروني غير المقروءة هو دالة لعدد الأيام. يعتمد عدد رسائل البريد الإلكتروني غير المقروءة، N، على عدد الأيام، t. لذلك، المتغير N، هو المتغير التابع والمتغير tt هو المتغير المستقل.

ⓑ ابحث$N(5)$. اشرح ما تعنيه هذه النتيجة.

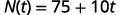
استبدل في t=5.t=5.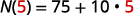
قم بالتبسيط.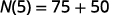

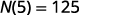
نظرًا لأن 5 هو عدد الأيام$N(5)$، فهو عدد رسائل البريد الإلكتروني غير المقروءة بعد 5 أيام. بعد 5 أيام، هناك 125 رسالة بريد إلكتروني غير مقروءة في الحساب.

مثال$\PageIndex{26}$

عدد رسائل البريد الإلكتروني غير المقروءة في حساب Bryan هو 100. يزداد هذا الرقم بمقدار 15 رسالة بريد إلكتروني غير مقروءة يوميًا. $N(t)=100+15t$تمثل الدالة العلاقة بين عدد رسائل البريد الإلكتروني، N، والوقت، t، المقاسة بالأيام.

1. حدد المتغير المستقل والمعتمد.
2. ابحث$N(7)]$. اشرح ما تعنيه هذه النتيجة.

إجابة

ⓐ T IND; N DEP ⓑ 2015; عدد رسائل البريد الإلكتروني غير المقروءة في حساب بريان في اليوم السابع.

مثال$\PageIndex{27}$

عدد رسائل البريد الإلكتروني غير المقروءة في حساب أنتوني هو 110. يزداد هذا الرقم بمقدار 25 رسالة بريد إلكتروني غير مقروءة يوميًا. $N(t)=110+25t$تمثل الدالة العلاقة بين عدد رسائل البريد الإلكتروني، N، والوقت، t، المقاسة بالأيام.

1. حدد المتغير المستقل والمعتمد.
2. ابحث$N(14)$. اشرح ما تعنيه هذه النتيجة.

إجابة

ⓐ t IND؛ N DEP ⓑ 460؛ عدد رسائل البريد الإلكتروني غير المقروءة في حساب أنتوني في اليوم الرابع عشر

قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة العلاقات والوظائف.

• مقدمة إلى الوظائف

المفاهيم الرئيسية

• تدوين الوظيفة: بالنسبة للوظيفة$y=f(x)$
  • f هو اسم الوظيفة
  • x هي قيمة المجال
  • $f(x)$هي قيمة النطاق y المقابلة للقيمة x التي
    نقرأها$f(x)$ كـ f of x أو قيمة f at x.
• المتغيرات المستقلة والمعتمدة: للوظيفة$y=f(x)$،
  • x هو المتغير المستقل حيث يمكن أن يكون أي قيمة في المجال
  • y هو المتغير التابع حيث تعتمد قيمته على x

مسرد المصطلحات

مجال العلاقة

مجال العلاقة هو جميع قيم x في الأزواج المرتبة من العلاقة.

وظيفة

الدالة هي علاقة تخصص لكل عنصر في مجاله عنصرًا واحدًا بالضبط في النطاق.

رسم الخرائط

يُستخدم التخطيط أحيانًا لإظهار العلاقة. تعرض الأسهم الاقتران بين عناصر المجال وعناصر النطاق.

نطاق العلاقة

نطاق العلاقة هو كل قيم y- في الأزواج المرتبة من العلاقة.

علاقة

العلاقة هي أي مجموعة من الأزواج المرتبة، (x، y). (س، ص). تشكل جميع قيم x في الأزواج المرتبة معًا المجال. تشكل جميع قيم y في الأزواج المرتبة معًا النطاق.