3.5: رسم بياني للمتباينات الخطية في متغيرين

Last updated
Save as PDF

Page ID: 201388

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

ملخص

في نهاية هذا القسم، ستكون قادرًا على:

تحقق من حلول عدم المساواة في متغيرين.
تعرف على العلاقة بين حلول عدم المساواة ورسمها البياني.
رسم بياني لعدم المساواة الخطية في متغيرين
حل التطبيقات باستخدام المتباينات الخطية في متغيرين

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

رسم بياني$x>2$ على خط الأعداد.
إذا فاتتك هذه المشكلة، راجع [link].
حل:$4x+3>23$.
إذا فاتتك هذه المشكلة، راجع [link].
ترجمة:$8<x>3$.
إذا فاتتك هذه المشكلة، راجع [link].

تحقق من حلول عدم المساواة في متغيرين

لقد تعلمنا سابقًا حل عدم المساواة بمتغير واحد فقط. سنتعرف الآن على عدم المساواة التي تحتوي على متغيرين. على وجه الخصوص، سننظر إلى عدم المساواة الخطية في متغيرين يشبهان إلى حد كبير المعادلات الخطية في متغيرين.

تحتوي عدم المساواة الخطية في متغيرين على العديد من التطبيقات. إذا كنت تدير نشاطًا تجاريًا، على سبيل المثال، فقد ترغب في أن تكون إيراداتك أكبر من تكاليفك - حتى يحقق نشاطك التجاري ربحًا.

عدم المساواة الخطية

عدم المساواة الخطية هي عدم مساواة يمكن كتابتها بأحد الأشكال التالية:

$ \begin{array} {l} { }& {Ax+By>C} &{Ax+By\geq C} &{Ax+By<C} &{Ax+By\leq C} \\ \end{array} $

حيث لا يكون كل من A و B صفرًا.

تذكر أن عدم المساواة مع متغير واحد له العديد من الحلول. على سبيل المثال، حل عدم المساواة x>3x>3 هو أي رقم أكبر من 3. أظهرنا ذلك على خط الأعداد من خلال التظليل في خط الأرقام على يمين 3، ووضع قوس مفتوح عند 3. انظر الشكل.

صورة خط الأعداد مع الأعداد الصحيحة من سالب 5 إلى 5. يتم تمييز جزء خط الأرقام الموجود على يمين 3 بخط أزرق. يتم وضع علامة على الرقم 3 بقوس أزرق مفتوح. — الشكل$\PageIndex{1}$

وبالمثل، فإن عدم المساواة الخطية في متغيرين لها العديد من الحلول. أي زوج مرتب (x، y) (x، y) يجعل عدم المساواة صحيحًا عندما نستبدل القيم هو حل لعدم المساواة الخطية.

حل عدم المساواة الخطية

$(x,y)$يعتبر الزوج المرتب حلاً لعدم المساواة الخطية إذا كان عدم المساواة صحيحًا عندما نستبدل قيم x و y.

فهرس الصفحات {1}\)

حدد ما إذا كان كل زوج مرتب يمثل حلاً لعدم المساواة y>x+4:y>x+4:

ⓐ (0,0) (0,0) ⓑ (1,6) (1,6) ⓒ (2,6) (2,6) ⓓ (−5, −15) (−5, −15) ⓔ (−8,12) (−8,12)

إجابة

ⓐ

$(0,0)$	$.$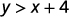
$.$	$.$
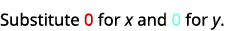
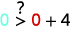
قم بالتبسيط.	$.$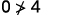
	لذلك،$(0,0)$ ليس حلاً لـ$y>x+4$.

ⓑ

$(1,6)$	$.$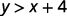
$.$	$.$
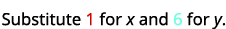
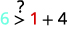
قم بالتبسيط.	$.$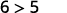
	لذلك،$(1,6)$ هو الحل لـ$y>x+4$.

ⓒ

$(2,6)$	$.$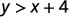
$.$	$.$
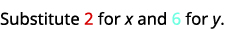
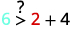
قم بالتبسيط.	$.$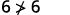
	لذلك،$(2,6)$ ليس حلاً لـ$y>x+4$.

ⓓ

$(−5,−15)$	$.$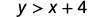
$.$	$.$
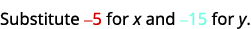
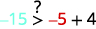
قم بالتبسيط.	$.$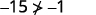
	لذلك،$(−5,−15)$ ليس حلاً لـ$y>x+4$.

ⓔ

$(−8,12)$	$.$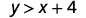
$.$	$.$
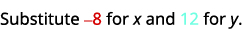
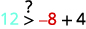
قم بالتبسيط.	$.$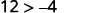
	لذلك،$(−8,12)$ هو الحل لـ$y>x+4$.

حدد ما إذا كان كل زوج مرتب حلاً لعدم المساواة$y>x−3$:

ⓐ$(0,0)$ ⓑ$(4,9)$ ⓒ$(−2,1)$ ⓓ$(−5,−3)$ ⓔ$(5,1)$

إجابة: ⓐ نعم ⓑ نعم ⓒ نعم ⓓ نعم ⓔ لا

مثال$\PageIndex{3}$

حدد ما إذا كان كل زوج مرتب حلاً لعدم المساواة$y<x+1$:

ⓐ$(0,0)$ ⓑ$(8,6)$ ⓒ$(−2,−1)$ ⓓ$(3,4)$ ⓔ$(−1,−4)$

إجابة: ⓐ نعم ⓑ نعم ⓒ لا ⓓ لا ⓔ نعم

تعرف على العلاقة بين حلول عدم المساواة ورسمها البياني

الآن، سننظر في كيفية ارتباط حلول عدم المساواة بالرسم البياني الخاص بها.

لنفكر في خط الأعداد الموضح سابقًا مرة أخرى. قامت النقطة$x=3$ بفصل خط الأرقام هذا إلى جزأين. على جانب واحد من 3 توجد جميع الأرقام الأقل من 3. على الجانب الآخر من 3، تكون جميع الأرقام أكبر من 3. انظر الشكل.

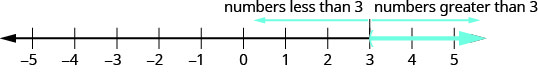
صورة خط الأعداد مع الأعداد الصحيحة من سالب 5 إلى 5. يتم تمييز جزء خط الأرقام الموجود على يمين 3 بخط أزرق. يتم وضع علامة على الرقم 3 بقوس أزرق مفتوح. يُطلق على جزء خط الأعداد الموجود على يمين الرقم 3 اسم «الأرقام الأكبر من 3". يُطلق على جزء خط الأعداد الموجود على يسار الرقم 3 اسم «الأرقام الأقل من 3". — الشكل$\PageIndex{2}$: الحل لـ$x>3$ هو الجزء المظلل من خط الأعداد على يمين$x=3$.

وبالمثل،$y=x+4$ يفصل الخط الطائرة إلى منطقتين. على جانب واحد من الخط توجد نقاط بـ$y<x+4$. على الجانب الآخر من الخط توجد النقاط ذات$y>x+4$. نسمي الخط$y=x+4$ خط الحدود.

خط الحدود

الخط مع المعادلة$Ax+By=C$ هو خط الحدود الذي يفصل المنطقة حيث$Ax+By>C$ من المنطقة$Ax+By<C$.

بالنسبة لعدم المساواة في متغير واحد، تظهر نقطة النهاية بقوس أو قوس اعتمادًا على ما إذا كان a مضمنًا في الحل أم لا:

$يتم عرض سطرين رقميين مع تسمية الوسط بالرقم «a». في كلا خطي الأرقام، يتم تمييز الجزء الموجود على يسار الرقم a باللون الأحمر. يُطلق على سطر الأرقام الأول اسم «x أقل من a» ويتم تمييز الرقم a بأقواس مفتوحة. يُطلق على سطر الأرقام الثاني اسم «x أقل من أو يساوي a» والرقم a مميز بقوس مفتوح.$

وبالمثل، بالنسبة لعدم المساواة في متغيرين، يظهر خط الحدود بخط صلب أو متقطع لإظهار ما إذا كان الخط مدرجًا في الحل أم لا.

\[ \begin{array} {ll} {Ax+By<C} &{Ax+By\leq C} \\ {Ax+By>C} &{Ax+By\geq C} \\ {\text{Boundary line is }Ax+By=C.} &{\text{Boundary line is }Ax+By=C.} \\ {\text{Boundary line is not included in solution.}} &{\text{Boundary line is not included in solution.}} \\ {\textbf{Boundary line is dashed.}} &{\textbf{Boundary line is solid.}} \\ \nonumber \end{array} \]

الآن، دعونا نلقي نظرة على ما وجدناه في المثال. سنبدأ برسم الخط$y=x+4$، ثم سنرسم النقاط الخمس التي اختبرناها، كما هو موضح في الرسم البياني. انظر الشكل.

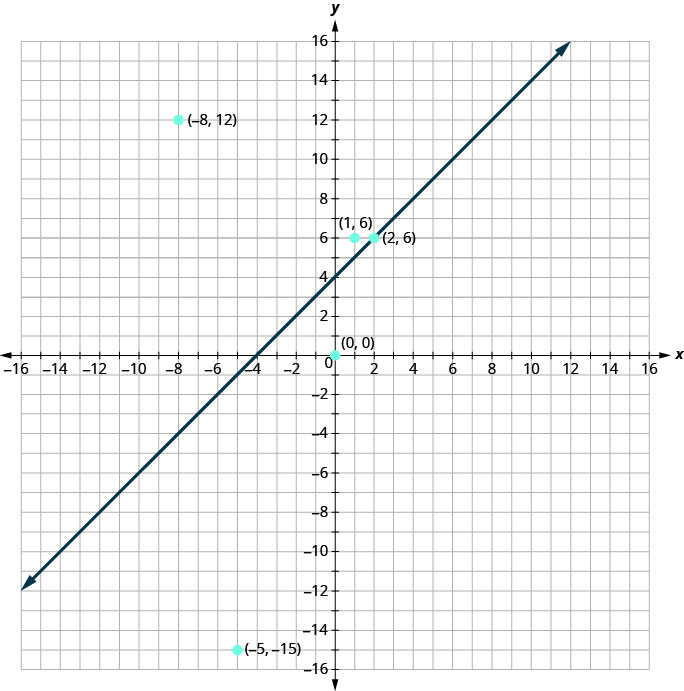
يحتوي هذا الشكل على رسم بياني لبعض النقاط وخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 16 إلى 16. يتم رسم النقاط (سالب 8، 12)، (سالب 5، سالب 15)، (0، 0)، (1، 6)، و (2، 6) وتسميتها بإحداثياتها. يتم رسم خط مستقيم من خلال النقاط (سالب 4، 0)، (0، 4)، (2، 6). — الشكل$\PageIndex{3}$

على سبيل المثال وجدنا أن بعض النقاط كانت حلولًا لعدم المساواة$y>x+4$ والبعض الآخر لم يكن كذلك.

أي من النقاط التي رسمناها هي حلول لعدم المساواة$y>x+4$؟

$(−8,12)$النقاط$(1,6)$ والحلول لعدم المساواة$y>x+4$. لاحظ أن كلاهما على نفس الجانب من خط الحدود$y=x+4$.

تقع$(0,0)$$(−5,−15)$ النقطتان على الجانب الآخر من خط الحدود$y=x+4$، وهما ليستا حلولاً لعدم المساواة$y>x+4$. بالنسبة لهاتين النقطتين،$y<x+4$.

ماذا عن النقطة$(2,6)$؟ لأن$6=2+4$ النقطة هي حل للمعادلة$y=x+4$، ولكنها ليست حلاً لعدم المساواة$y>x+4$. لذا فإن النقطة$(2,6)$ تقع على خط الحدود.

لنأخذ نقطة أخرى فوق خط الحدود ونختبر ما إذا كانت حلاً لعدم المساواة أم لا$y>x+4$. تبدو النقطة$(0,10)$ بوضوح فوق خط الحدود، أليس كذلك؟ هل هو حل لعدم المساواة؟

\[\begin{array} {lll} {y} &{>} &{x+4} \\ {10} &{\overset{?}{>}} &{0+4} \\ {10} &{>} &{4} \\ \nonumber \end{array}\]

لذلك،$(0,10)$ هو الحل لـ$y>x+4$.

أي نقطة تختارها فوق خط الحدود هي حل لعدم المساواة$y>x+4$. جميع النقاط فوق خط الحدود هي حلول.

وبالمثل، فإن جميع النقاط الموجودة أسفل خط الحدود، والجانب مع$(0,0)$ و$(−5,−15)$، ليست حلولًا لها$y>x+4$، كما هو موضح في الشكل.

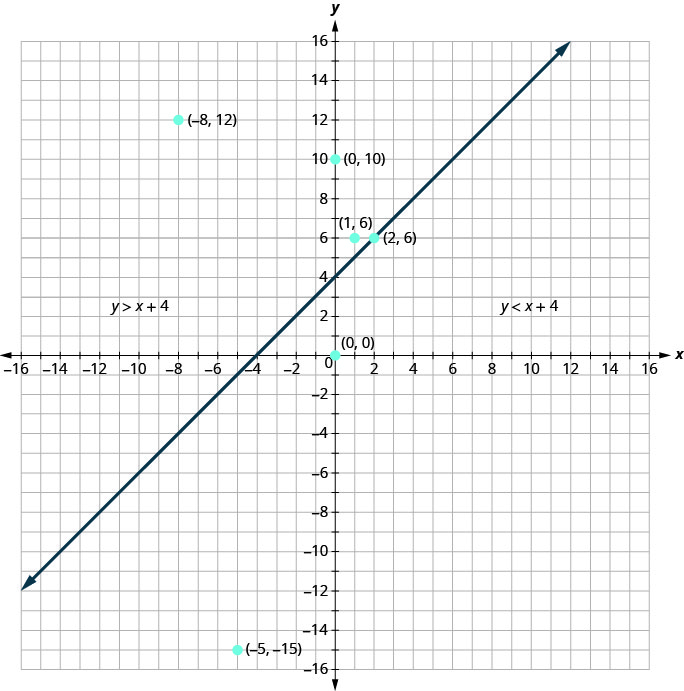
يظهر الرسم البياني$y>x+4$ لعدم المساواة أدناه.

$y=x+4$يقسم الخط الطائرة إلى منطقتين. يُظهر الجانب المظلل حلول لعدم المساواة$y>x+4$.

النقاط الموجودة على خط الحدود، تلك التي توجد فيها$y=x+4$، ليست حلولًا لعدم المساواة$y>x+4$، وبالتالي فإن الخط نفسه ليس جزءًا من الحل. نظهر ذلك من خلال جعل الخط متقطعًا وليس صلبًا.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم متقطع من خلال النقاط (سالب 4، 0)، (0، 4)، (2، 6). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيسر ملون باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

مثال$\PageIndex{4}$

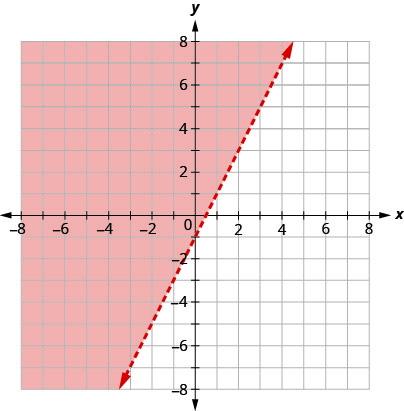
خط الحدود الموضح في هذا الرسم البياني هو$y=2x−1$. اكتب عدم المساواة التي يوضحها الرسم البياني.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم متقطع من خلال النقاط (0، سالب 1)، (1، 1)، (2، 3). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيسر ملون باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

إجابة

الخط$y=2x−1$ هو خط الحدود. على أحد جانبي الخط توجد النقاط$y>2x−1$ ذات النقاط الموجودة على الجانب الآخر من الخط$y<2x−1$.

دعونا نختبر النقطة$(0,0)$ ونرى عدم المساواة التي تصف موضعها بالنسبة لخط الحدود.

في$(0,0)$ أي من حالات عدم المساواة صحيحة:$y>2x−1$ أم$y<2x−1$؟

\[\begin{array} {ll} {y>2x−1} &{y<2x−1} \\ {0\overset{?}{>}2·0−1} &{0\overset{?}{<}2·0−1} \\ {0>−1\text{ True}} &{0<−1\text{ False}} \\ \nonumber \end{array}\]

بما$y>2x−1$ أن جانب الخط مع، صحيح$(0,0)$، هو الحل. تُظهر المنطقة المظللة حل عدم المساواة$y>2x−1$.

بما أن خط الحدود مرسوم بخط صلب، فإن عدم المساواة يتضمن علامة التساوي.

يوضِّح الرسم البياني عدم المساواة$y\geq 2x−1$.

يمكننا استخدام أي نقطة كنقطة اختبار، بشرط ألا تكون على الخط. لماذا اخترنا$(0,0)$؟ لأنه الأسهل في التقييم. قد ترغب في اختيار نقطة على الجانب الآخر من خط الحدود والتحقق من ذلك$y<2x−1$.

مثال$\PageIndex{5}$

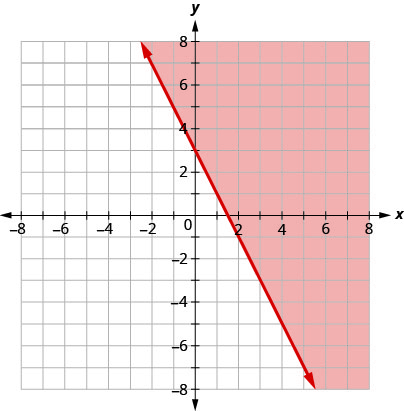
اكتب عدم المساواة التي يوضحها الرسم البياني مع خط الحدود$y=−2x+3$.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم من خلال النقاط (0، 3)، (1، 1)، (3، سالب 3). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تلوين الخط نفسه والنصف العلوي الأيمن باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

إجابة: $y\geq −2x+3$

مثال$\PageIndex{6}$

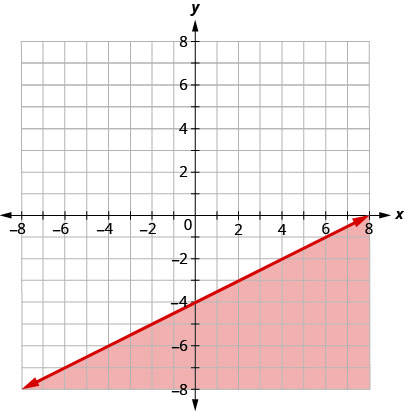
اكتب عدم المساواة التي يوضحها الرسم البياني مع خط الحدود$y=\frac{1}{2}x−4$.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم من خلال النقاط (0، سالب 4)، (2، سالب 3)، (4، سالب 2). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تلوين الخط نفسه والنصف السفلي الأيمن باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

إجابة: $y\leq \frac{1}{2}x−4$

مثال$\PageIndex{7}$

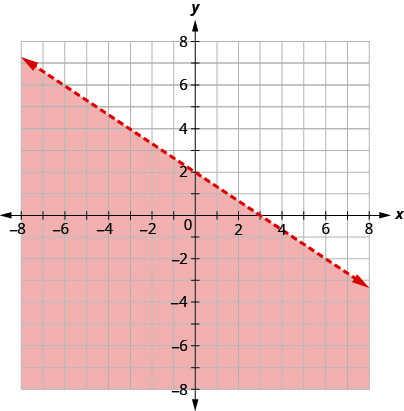
خط الحدود الموضح في هذا الرسم البياني هو$2x+3y=6$. اكتب عدم المساواة التي يوضحها الرسم البياني.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم متقطع من خلال النقاط (0، 2)، (3، 0)، (6، سالب 2). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف السفلي الأيسر ملون باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

إجابة

الخط$2x+3y=6$ هو خط الحدود. على أحد جانبي الخط توجد النقاط$2x+3y>6$ ذات النقاط الموجودة على الجانب الآخر من الخط$2x+3y<6$.

دعونا نختبر النقطة$(0,0)$ ونرى عدم المساواة التي تصف جانبها من خط الحدود.

في$(0,0)$ أي من حالات عدم المساواة صحيحة:$2x+3y>6$ أم$2x+3y<6$؟

\[\begin{array} {ll} {2x+3y>6} &{2x+3y<6} \\ {2(0)+3(0)\overset{?}{>}6} &{2(0)+3(0)\overset{?}{<}6} \\ {0>6\text{ False}} &{0<6\text{ True}} \\ \nonumber \end{array}\]

لذا فإن الجانب الأول$(0,0)$ هو الجانب الذي فيه$2x+3y<6$.

(قد ترغب في اختيار نقطة على الجانب الآخر من خط الحدود والتحقق من ذلك$2x+3y>6$.)

بما أن خط الحدود مرسوم بيانيًا كخط متقطع، فإن عدم المساواة لا يتضمن علامة المساواة.

تُظهر المنطقة المظللة الحل لعدم المساواة$2x+3y<6$.

مثال$\PageIndex{8}$

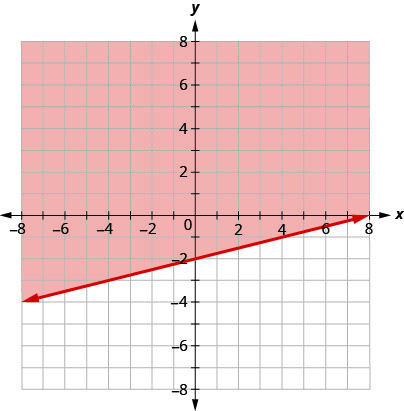
اكتب عدم المساواة التي تظهرها المنطقة المظللة في الرسم البياني مع خط الحدود$x−4y=8$.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم من خلال النقاط (0، سالب 2)، (4، سالب 1)، (8، 0). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تلوين الخط نفسه والنصف العلوي الأيسر باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

إجابة: $x−4y\leq 8$

مثال$\PageIndex{9}$

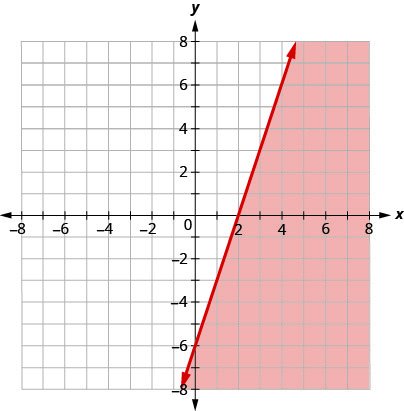
اكتب عدم المساواة التي تظهرها المنطقة المظللة في الرسم البياني مع خط الحدود$3x−y=6$.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم من خلال النقاط (0، سالب 6)، (1، سالب 3)، (2، 0). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تلوين الخط نفسه والنصف السفلي الأيمن باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

إجابة: $3x−y\geq 6$

رسم بياني متباينات خطية في متغيرين

الآن بعد أن عرفنا كيف يبدو الرسم البياني للتفاوت الخطي وكيفية ارتباطه بالمعادلة الحدودية، يمكننا استخدام هذه المعرفة لرسم عدم مساواة خطية معينة.

مثال$\PageIndex{10}$: How to Graph a Linear Equation in Two Variables

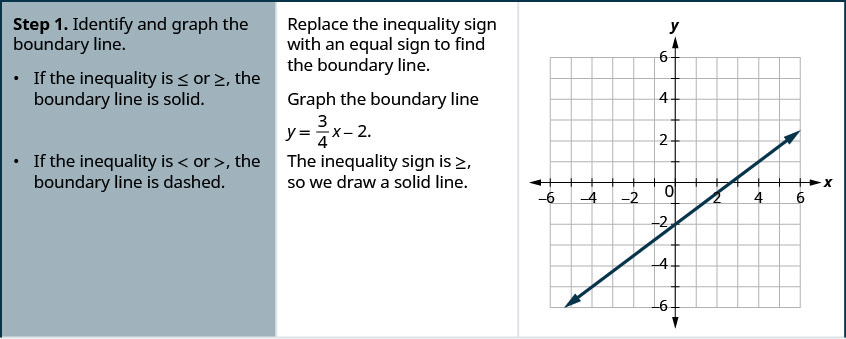
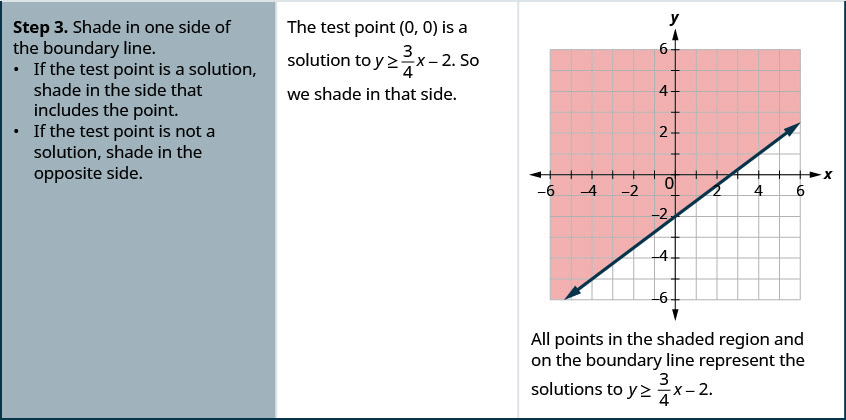
رسم بياني للتفاوت الخطي$y\geq \frac{3}{4}x−2$.

إجابة: $الخطوة 1 هي تحديد خط الحدود ورسمه. إذا كان عدم المساواة أقل من أو يساوي أو أكبر من أو يساوي، يكون خط الحدود صلبًا. إذا كان عدم المساواة أقل من أو أكبر من، يكون خط الحدود متقطعًا. في هذا المثال، تكون علامة عدم المساواة أكبر من أو تساوي، لذلك نرسم خطًا صلبًا. استبدل علامة عدم المساواة بعلامة المساواة للعثور على خط الحدود. رسم بياني لخط الحدود y = 3 مقسومًا على 4 مرات x ناقص 2. ثم يوضِّح الشكل الرسم البياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 12 إلى 12. يمر الخط بالنقاط (0، سالب 2)، (4، 1)، و (8، 4).$ $الخطوة 2 هي اختبار نقطة ليست على خط الحدود. هل هو حل لعدم المساواة؟ سنختبر (0، 0). عند (0، 0) يكون y أكبر من أو يساوي 3 مقسومًا على 4 في x ناقص 2؟ هل 0 أكبر من أو يساوي 3 مقسومًا على 4 في 0 ناقص 2؟ 0 أكبر من أو يساوي سالب 2 لذا (0، 0) هو الحل.$ $الخطوة 3 هي التظليل في جانب واحد من خط الحدود. إذا كانت نقطة الاختبار عبارة عن حل، فقم بالتظليل في الجانب الذي يتضمن النقطة. إذا لم تكن نقطة الاختبار حلاً، فقم بالتظليل في الجانب الآخر. نقطة الاختبار (0، 0) هي حل لـ y أكبر من أو يساوي 3 مقسومًا على 4 مرات x ناقص 2. لذلك نقوم بالتظليل في الجانب الذي يحتوي على (0، 0). ثم يوضِّح الشكل الرسم البياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 12 إلى 12. يمر الخط بالنقاط (0، سالب 2)، (4، 1)، و (8، 4). يتم تظليل النصف العلوي الأيسر من المستوى الإحداثي للإشارة إلى أن هذا هو المكان الذي توجد فيه مجموعة الحلول.$

مثال$\PageIndex{11}$

رسم بياني للتفاوت الخطي$y>\frac{5}{2}x−4$.

إجابة

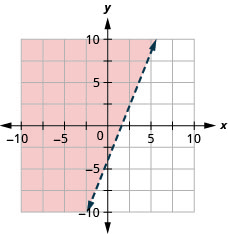
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط مستقيم متقطع من خلال النقاط (0، سالب 4)، (2، 1)، (4، 6). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيسر مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة وعلى خط الحدود الحلول لـ$y>\frac{5}{2}x−4$.

مثال$\PageIndex{12}$

رسم بياني للتفاوت الخطي$y<\frac{2}{3}x−5$.

إجابة

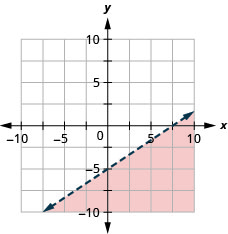
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط مستقيم متقطع من خلال النقاط (0، سالب 5)، (3، سالب 3)، (5، سالب 1). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيسر مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة، ولكن ليس تلك الموجودة على خط الحدود، الحلول لـ$y<\frac{2}{3}x−5$.

يتم تلخيص الخطوات التي نتخذها لرسم عدم المساواة الخطية هنا.

رسم بياني لتفاوت خطي في متغيرين.

حدد خط الحدود ورسمًا بيانيًا.
- إذا كان عدم المساواة هو\ leq أو\ geq أو\ geq، يكون خط الحدود صلبًا.
- إذا كانت عدم المساواة هي <or><or>، فإن خط الحدود متقطع.
اختبر نقطة ليست على خط الحدود. هل هو حل لعدم المساواة؟
ظل في جانب واحد من خط الحدود.
- إذا كانت نقطة الاختبار عبارة عن حل، فقم بالتظليل في الجانب الذي يتضمن النقطة.
- إذا لم تكن نقطة الاختبار حلاً، فقم بالتظليل في الجانب الآخر.

مثال$\PageIndex{13}$

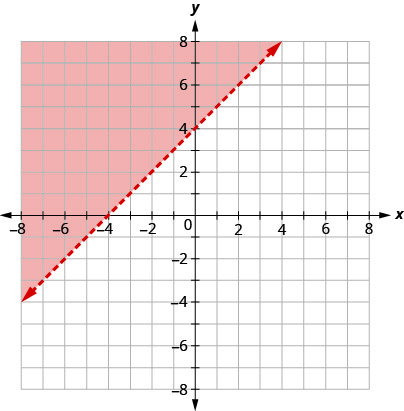
رسم بياني للتفاوت الخطي$x−2y<5$.

إجابة

أولاً، نرسم خط الحدود$x−2y=5$. عدم المساواة هو$<$ أننا نرسم خطًا متقطعًا.

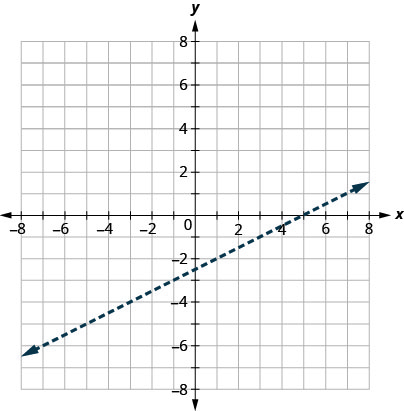
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم متقطع من خلال النقاط (سالب 3، سالب 4)، (1، سالب 2)، (5، 0).$

ثم نختبر نقطة ما. سنستخدمها$(0,0)$ مرة أخرى لأنها سهلة التقييم وليست على خط الحدود.

هو$(0,0)$ حل لـ$x−2y<5$؟

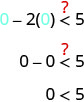
$هل 0 ناقص مرتين في 0 أقل من 5؟ هل 0 ناقص 0 أقل من 5؟ 0 أقل من 5.$

النقطة$(0,0)$ هي الحل$x−2y<5$، لذلك نحن نغلق في هذا الجانب من خط الحدود.

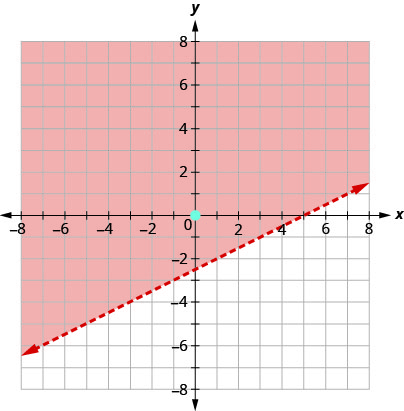
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط مستقيم متقطع من خلال النقاط (سالب 3، سالب 4)، (1، سالب 2)، (5، 0). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيسر مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة، ولكن ليس تلك الموجودة على خط الحدود، الحلول لـ$x−2y<5$.

مثال$\PageIndex{14}$

رسم بياني لعدم المساواة الخطية:$2x−3y<6$.

إجابة

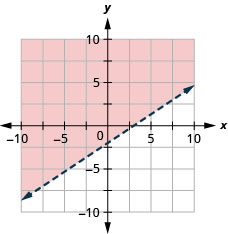
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط مستقيم متقطع من خلال النقاط (0، سالب 2)، (3، 0)، (6، 2). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيسر مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة، ولكن ليس تلك الموجودة على خط الحدود، الحلول لـ$2x−3y<6$.

مثال$\PageIndex{15}$

رسم بياني لعدم المساواة الخطية:$2x−y>3$.

إجابة

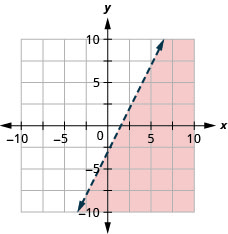
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط مستقيم متقطع من خلال النقاط (0، سالب 3)، (1، سالب 1)، و (2، 1). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف السفلي الأيمن مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة، ولكن ليس تلك الموجودة على خط الحدود، الحلول لـ$2x−y>3$.

ماذا لو كان خط الحدود يمر عبر نقطة الأصل؟ بعد ذلك، لن نتمكن من استخدامها$(0,0)$ كنقطة اختبار. لا توجد مشكلة - سنختار فقط نقطة أخرى ليست على خط الحدود.

مثال$\PageIndex{16}$

رسم بياني لعدم المساواة الخطية:$y\leq −4x$.

إجابة

أولاً، نرسم خط الحدود$y=−4x$. وهو في شكل منحدر ومعترض، مع$m=−4$ و$b=0$. عدم المساواة هو$\leq$ أننا نرسم خطًا صلبًا.

$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم مستقيم من خلال النقاط (0، 0)، (1، سالب 4)، و (سالب 1، 4).$

الآن نحن بحاجة إلى نقطة اختبار. يمكننا أن نرى أن النقطة (1,0) (1,0) ليست على خط الحدود.

هو$(1,0)$ حل لـ$y\leq −4x$؟

$.$

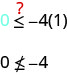
هذه النقطة$(1,0)$ ليست حلاً لها$y\leq −4x$، لذلك نتظليل في الجانب الآخر من خط الحدود.

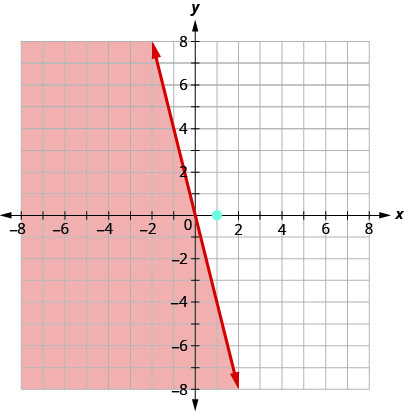
$هل 0 أقل من أو يساوي سالب 4 في 1؟ 0 لا يقل عن أو يساوي سالب 4.$

تمثل جميع النقاط في المنطقة المظللة وعلى خط الحدود الحلول لـ$y\leq −4x$.

مثال$\PageIndex{17}$

رسم بياني لعدم المساواة الخطية:$y>−3x$.

إجابة

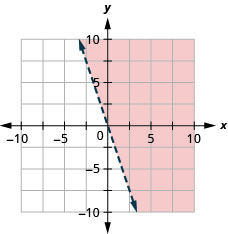
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط مستقيم متقطع من خلال النقاط (سالب 1، 3)، (0، 0)، (1، سالب 3). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيمن مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة، ولكن ليس تلك الموجودة على خط الحدود، الحلول لـ$y>−3x$.

مثال$\PageIndex{18}$

رسم بياني لعدم المساواة الخطية:$y\geq −2x$.

إجابة

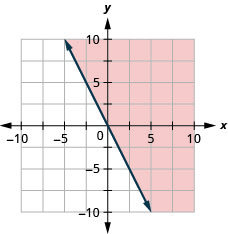
$يحتوي هذا الشكل على رسم بياني لخط مستقيم متقطع على مستوى الإحداثيات x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط مستقيم متقطع من خلال النقاط (سالب 1، 2)، (0، 0)، (1، سالب 2). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي الأيمن مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة وعلى خط الحدود الحلول لـ$y\geq −2x$.

تحتوي بعض المتباينات الخطية على متغير واحد فقط. قد يكون لديهم x ولكن ليس y، أو y ولكن لا x. في هذه الحالات، سيكون خط الحدود إما خطًا رأسيًا أو أفقيًا.

تذكر أن:

\[\begin{array} {ll} {x=a} &{\text{vertical line}} \\ {y=b} &{\text{horizontal line}} \\ \nonumber \end{array}\]

مثال$\PageIndex{19}$

رسم بياني لعدم المساواة الخطية:$y>3$.

إجابة

أولاً، نرسم خط الحدود$y=3$. إنه خط أفقي. عدم المساواة هو$>$ أننا نرسم خطًا متقطعًا.

نحن نختبر هذه النقطة$(0,0)$.

\[y>3\nonumber\]\[0\slashed{>}3\nonumber\]

لذلك،$(0,0)$ ليس حلاً لـ$y>3$.

لذلك نقوم بتظليل الجانب الذي لا يتضمن$(0,0)$ كما هو موضح في هذا الرسم البياني.

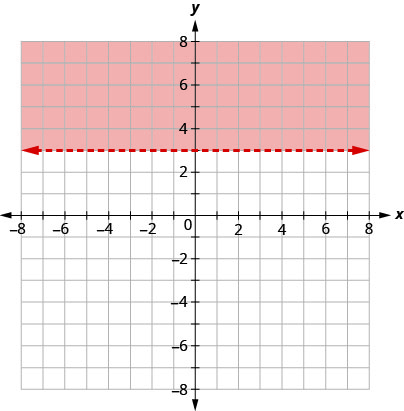
$يحتوي هذا الشكل على رسم بياني لخط أفقي متقطع مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 8 إلى 8. يتم رسم خط أفقي متقطع من خلال النقاط (سالب 1، 3)، (0، 3)، و (1، 3). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف العلوي مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة، ولكن ليس تلك الموجودة على خط الحدود، الحلول لـ$y>3$.

مثال$\PageIndex{20}$

رسم بياني لعدم المساواة الخطية:$y<5$.

إجابة

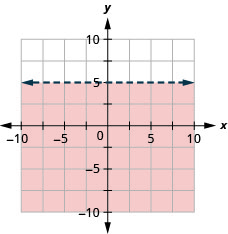
$يحتوي هذا الشكل على رسم بياني لخط أفقي متقطع مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط أفقي متقطع من خلال النقاط (سالب 1، 5)، (0، 5)، و (1، 5). يقسم الخط المستوى الإحداثي x y إلى نصفين. النصف السفلي مظلل باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة، ولكن ليس تلك الموجودة على خط الحدود، الحلول لـ$y<5$.

مثال$\PageIndex{21}$

رسم بياني لعدم المساواة الخطية:$y\leq −1$.

إجابة

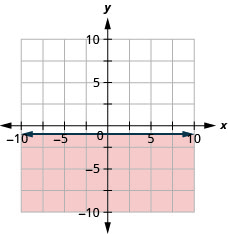
$يحتوي هذا الشكل على رسم بياني لخط أفقي مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من سالب 10 إلى 10. يتم رسم خط أفقي من خلال النقاط (سالب 1، سالب 1)، (0، سالب 1)، (1، سالب 1). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تظليل الخط والنصف السفلي باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

تمثل جميع النقاط في المنطقة المظللة وعلى خط الحدود الحلول لـ$y\leq −1$.

حل التطبيقات باستخدام المتباينات الخطية في متغيرين

تستخدم العديد من الحقول عدم المساواة الخطية لنمذجة المشكلة. في حين أن أمثلتنا قد تكون حول مواقف بسيطة، إلا أنها تمنحنا فرصة لبناء مهاراتنا والتعرف على كيفية استخدام ذلك.

مثال$\PageIndex{22}$

تعمل هيلاريا في وظيفتين بدوام جزئي من أجل كسب ما يكفي من المال للوفاء بالتزاماتها التي لا تقل عن 240 دولارًا في الأسبوع. تدفع وظيفتها في خدمة الطعام 10 دولارات في الساعة وتدفع وظيفتها التعليمية في الحرم الجامعي 15 دولارًا في الساعة. كم عدد الساعات التي تحتاجها هيلاريا للعمل في كل وظيفة لكسب 240 دولارًا على الأقل؟

ⓐ اجعل xx هو عدد الساعات التي تعمل فيها في الوظيفة في خدمة الطعام ودع y يكون عدد الساعات التي تعمل فيها في التدريس. اكتب عدم المساواة التي من شأنها أن تمثل هذا الموقف.

ⓑ رسم بياني لعدم المساواة.

إجابة

ⓐ نسمح لـ x أن يكون عدد الساعات التي تعمل فيها في الوظيفة في خدمة الطعام ودعنا يكون عدد الساعات التي تعمل فيها في التدريس.

تكسب 10 دولارات في الساعة في العمل في خدمة الطعام و 15 دولارًا في الساعة من التدريس. في كل وظيفة، سيعطي عدد الساعات مضروبًا في الأجر بالساعة المبلغ المكتسب في تلك الوظيفة.

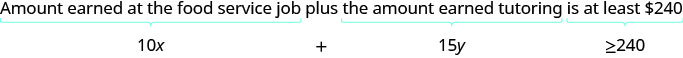
$10 x زائد 15 y أكبر من 240. يُطلق على «10x» اسم «المبلغ المكتسب في وظيفة خدمة الطعام». يُطلق على «15 y» اسم «المبلغ المكتسب من الدروس الخصوصية». يُطلق على «أكبر من 240" اسم «لا يقل عن 240".$

ⓑ لرسم عدم المساواة بيانيًا، نضعها في شكل منحدر - تقاطع.

\[\begin{align} {10x+15y} &\geq 240 \\ 15y &\geq -10x+240 \\ y &\geq {−\frac{2}{3}x+16} \\ \nonumber \end{align}\]

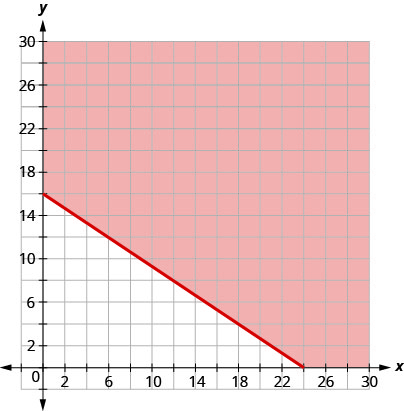
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من 0 إلى 25. يتم رسم خط من خلال النقاط (0، 16)، (15، 6)، (24، 0). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تظليل الخط والنصف العلوي الأيمن باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

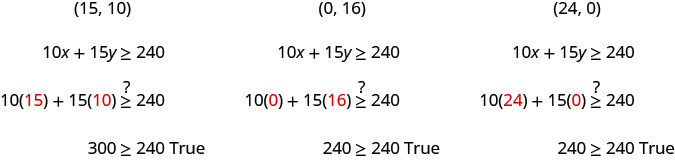
$نختبر أولاً النقطة (15، 10) في عدم المساواة التي تبلغ 10 x زائد 15 y أكبر من أو تساوي 240. هل العدد ١٠ في ١٥ زائد ١٥ في ١٠ أكبر من أو يساوي ٢٤٠؟ نظرًا لأن 300 أكبر من أو يساوي 240 (15، 10) يعد الحل. بعد ذلك نختبر النقطة (0، 16) في عدم المساواة 10 x زائد 15 y أكبر من أو يساوي 240. هل العدد ١٠ في ٠ زائد ١٥ في ١٦ أكبر من أو يساوي ٢٤٠؟ نظرًا لأن 240 أكبر من أو يساوي 240 (0، 16) يعد الحل. ثم نختبر النقطة (24، 0) في عدم المساواة 10 x زائد 15 y أكبر من أو يساوي 240. هل العدد ١٠ في ٢٤ زائد ١٥ في ٠ أكبر من أو يساوي ٢٤٠؟ نظرًا لأن 240 أكبر من أو يساوي 240 (24، 0) يعد الحل.$

بالنسبة لهيلاريا، يعني ذلك أنه لكسب 240 دولارًا على الأقل، يمكنها العمل لمدة 15 ساعة في التدريس و 10 ساعات في وظيفتها للوجبات السريعة، أو كسب كل أموالها من الدروس الخصوصية لمدة 16 ساعة، أو كسب كل أموالها أثناء العمل لمدة 24 ساعة في العمل في خدمة الطعام.

مثال$\PageIndex{23}$

يعمل هيو في وظيفتين بدوام جزئي. أحدهما في محل بقالة يدفع 10 دولارات في الساعة والآخر في مجالسة الأطفال لمدة 13 دولارًا في الساعة. بين الوظيفتين، يريد هيو كسب 260 دولارًا على الأقل في الأسبوع. كم عدد الساعات التي يحتاجها هيو للعمل في كل وظيفة لكسب 260 دولارًا على الأقل؟

ⓐ اجعل x هو عدد الساعات التي يعمل فيها في محل البقالة وليكن عدد الساعات التي يعمل فيها في مجالسة الأطفال. اكتب عدم المساواة التي من شأنها أن تمثل هذا الموقف.

ⓑ رسم بياني لعدم المساواة.

إجابة

ⓐ$10x+13y\geq 260$
ⓑ

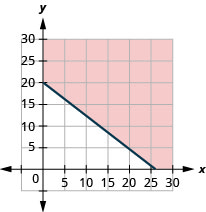
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من 0 إلى 30. يتم رسم خط من خلال النقاط (0، 20)، (13، 10)، (26، 0). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تظليل الخط والنصف العلوي الأيمن باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

مثال$\PageIndex{24}$

تعمل فيرونيكا في وظيفتين بدوام جزئي من أجل كسب ما يكفي من المال للوفاء بالتزاماتها التي لا تقل عن 280 دولارًا في الأسبوع. تدفع وظيفتها في السبا النهاري 10 دولارات في الساعة وتدفع وظيفتها المساعدة الإدارية في الحرم الجامعي 17.50 دولارًا في الساعة. كم عدد الساعات التي تحتاجها فيرونيكا للعمل في كل وظيفة لكسب 280 دولارًا على الأقل؟

ⓐ اجعل x هو عدد ساعات عملها في المنتجع الصحي النهاري ودع y يكون عدد الساعات التي تعمل فيها كمساعد إداري. اكتب عدم المساواة التي من شأنها أن تمثل هذا الموقف.

ⓑ رسم بياني لعدم المساواة.

إجابة

ⓐ$10x+17.5y\geq 280$
ⓑ

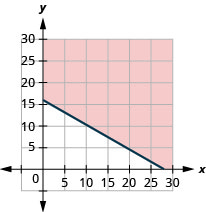
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على المستوى الإحداثي x y. يتم تشغيل محاور x و y من 0 إلى 25. يتم رسم خط من خلال النقاط (0، 16) و (28، 0). يقسم الخط المستوى الإحداثي x y إلى نصفين. تم تظليل الخط والنصف العلوي الأيمن باللون الأحمر للإشارة إلى أن هذا هو المكان الذي توجد فيه حلول عدم المساواة.$

يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع رسم التفاوتات الخطية بيانيًا في متغيرين.

التمثيل البياني للمتباينات الخطية في متغيرين

المفاهيم الرئيسية

كيفية رسم بياني لعدم المساواة الخطية في متغيرين.
1. حدد خط الحدود ورسمًا بيانيًا.
  إذا كان عدم المساواة هو$\leq$ أو$\geq$، يكون خط الحدود صلبًا.
  إذا كان عدم المساواة هو$<$ أو$>$، يكون خط الحدود متقطعًا.
2. اختبر نقطة ليست على خط الحدود. هل هو حل لعدم المساواة؟
3. ظل في جانب واحد من خط الحدود.
  إذا كانت نقطة الاختبار عبارة عن حل، فقم بالتظليل في الجانب الذي يتضمن النقطة.
  إذا لم تكن نقطة الاختبار حلاً، فقم بالتظليل في الجانب الآخر.

مسرد المصطلحات

خط الحدود: الخط مع المعادلة$Ax+By=C$ هو خط الحدود الذي يفصل المنطقة حيث$Ax+By>C$ من المنطقة$Ax+By<C$.

عدم المساواة الخطية: عدم المساواة الخطية هي عدم مساواة يمكن كتابتها بأحد الأشكال التالية: أو أو، أو$Ax+By>C$$Ax+By\geq C$$Ax+By<C$$Ax+By\leq C$، حيث لا يكون كل من A و B صفرًا.

حل لعدم المساواة الخطية: $(x,y)$يعتبر الزوج المرتب حلاً لعدم المساواة الخطية إذا كان عدم المساواة صحيحًا عندما نستبدل قيم x و y.

عدم المساواة الخطية

حل عدم المساواة الخطية

فهرس الصفحات {1}\)

مثال\(\PageIndex{3}\)

خط الحدود

مثال\(\PageIndex{4}\)

مثال\(\PageIndex{5}\)

مثال\(\PageIndex{6}\)

مثال\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)

مثال\(\PageIndex{10}\): How to Graph a Linear Equation in Two Variables

مثال\(\PageIndex{11}\)

مثال\(\PageIndex{12}\)

رسم بياني لتفاوت خطي في متغيرين.

مثال\(\PageIndex{13}\)

مثال\(\PageIndex{14}\)

مثال\(\PageIndex{15}\)

مثال\(\PageIndex{16}\)

مثال\(\PageIndex{17}\)

مثال\(\PageIndex{18}\)

مثال\(\PageIndex{19}\)

مثال\(\PageIndex{20}\)

مثال\(\PageIndex{21}\)

مثال\(\PageIndex{22}\)

مثال\(\PageIndex{23}\)

مثال\(\PageIndex{24}\)

\((0,0)\)	$.$
$.$	$.$
قم بالتبسيط.	$.$
	لذلك،\((0,0)\) ليس حلاً لـ\(y>x+4\).

\((1,6)\)	$.$
$.$	$.$
قم بالتبسيط.	$.$
	لذلك،\((1,6)\) هو الحل لـ\(y>x+4\).

\((2,6)\)	$.$
$.$	$.$
قم بالتبسيط.	$.$
	لذلك،\((2,6)\) ليس حلاً لـ\(y>x+4\).

\((−5,−15)\)	$.$
$.$	$.$
قم بالتبسيط.	$.$
	لذلك،\((−5,−15)\) ليس حلاً لـ\(y>x+4\).

\((−8,12)\)	$.$
$.$	$.$
قم بالتبسيط.	$.$
	لذلك،\((−8,12)\) هو الحل لـ\(y>x+4\).