3.4E: تمارين

Last updated
Save as PDF

Page ID: 201404

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

الممارسة تجعل من الكمال

أوجد معادلة الخط المستقيم بمعلومية المنحدر والجزء المقطوع من محور الصادات

في التمارين التالية، أوجد معادلة الخط المستقيم الذي يحتوي على ميل معطى والجزء المقطوع من محور y. اكتب المعادلة في صورة تقاطع منحدر.

1. المنحدر$3$$y$ والاعتراض$(0,5)$

إجابة: $y=3x+5$

2. المنحدر$8$$y$ والاعتراض$(0,−6)$

3. المنحدر$−3$$y$ والاعتراض$(0,−1)$

إجابة: $y=−3x−1$

4. المنحدر$−1$$y$ والاعتراض$(0,3)$

5. المنحدر$\frac{1}{5}$$y$ والاعتراض$(0,−5)$

إجابة: $y=\frac{1}{5}x−5$

6. المنحدر$−\frac{3}{4}$$y$ والاعتراض$(0,−2)$

7. المنحدر$0$$y$ والاعتراض$(0,−1)$

إجابة: $y=−1$

8. المنحدر$−4$$y$ والاعتراض$(0,0)$

في التمارين التالية، ابحث عن معادلة الخط المستقيم الموضح في كل رسم بياني. اكتب المعادلة في صورة تقاطع منحدر.

9.
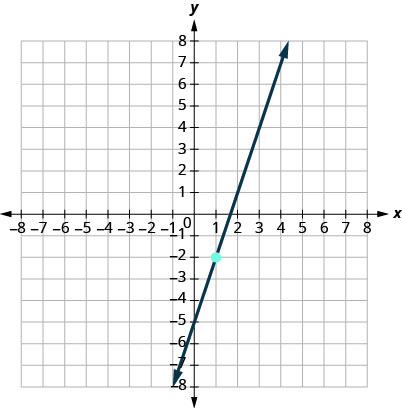
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، سالب 5)، (1، سالب 2)، و (2، 1).$

إجابة: $y=3x−5$

10.
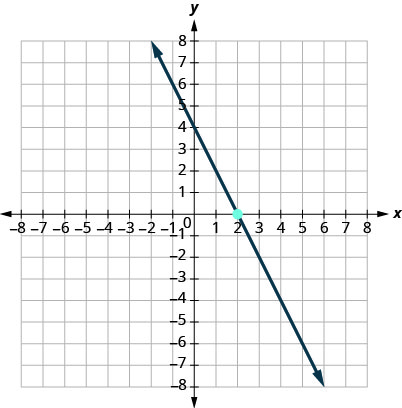
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، 4)، (1، 2)، و (2، 0).$

11.
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، سالب 3)، (2، سالب 2)، و (6، 0).$

إجابة: $y=\frac{1}{2}x−3$

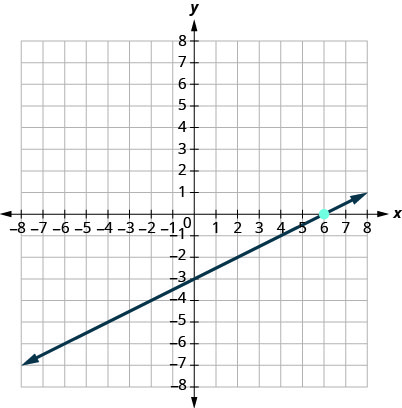
12.
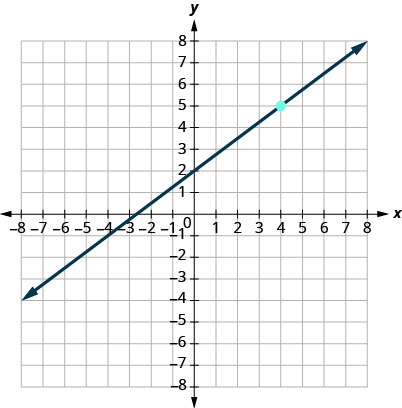
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، 2)، (4، 5)، و (8، 8).$

13.
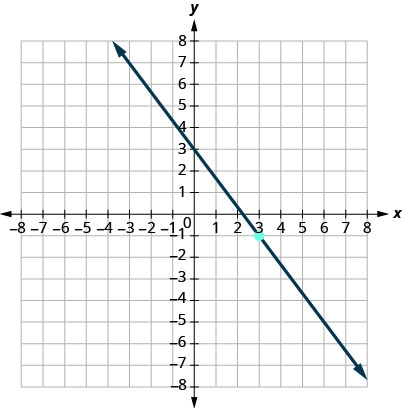
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، 3)، (3، سالب 1)، و (6، سالب 5).$

إجابة: $y=−\frac{4}{3}x+3$

14.
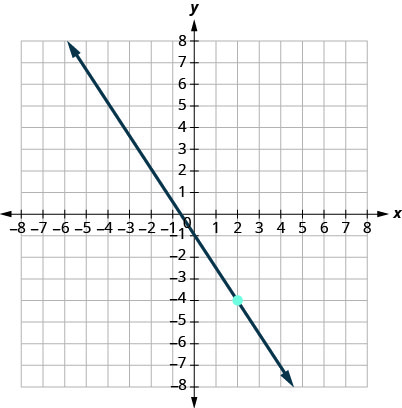
$يحتوي هذا الشكل على رسم بياني لخط مستقيم على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، سالب 1)، (2، سالب 4)، و (4، سالب 7).$

15.
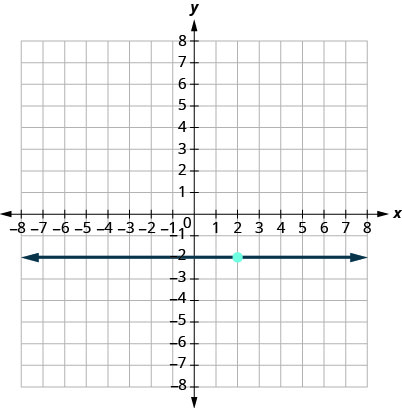
$يحتوي هذا الشكل على رسم بياني لخط مستقيم أفقي على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، سالب 2)، (1، سالب 2)، و (2، سالب 2).$

إجابة: $y=−2$

16.
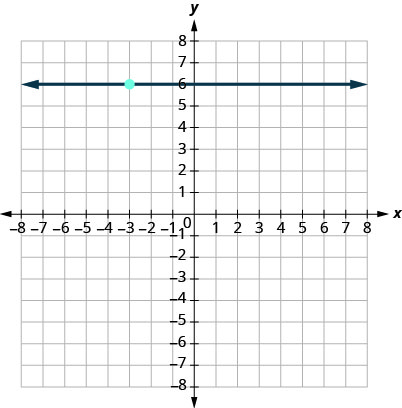
$يحتوي هذا الشكل على رسم بياني لخط مستقيم أفقي على مستوى الإحداثيات x y. يمتد المحوران x و y من سالب 10 إلى 10. يمر الخط بالنقاط (0، 6)، (1، 6)، و (2، 6).$

أوجد معادلة الخط المستقيم بمعلومية الميل والنقطة

في التمارين التالية، أوجد معادلة الخط المستقيم الذي يحتوي على ميل معطى ويحتوي على النقطة المُعطاة. اكتب المعادلة في صورة تقاطع منحدر.

17. $m=\frac{5}{8}$، نقطة$(8,3)$

إجابة: $y=\frac{5}{8}x−2$

18. $m=\frac{5}{6}$، نقطة$(6,7)$

19. $m=−\frac{3}{5}$، نقطة$(10,−5)$

إجابة: $y=−\frac{3}{5}x+1$

20. $m=−\frac{3}{4}$، نقطة$(8,−5)$

21. $m=−\frac{3}{2}$، نقطة$(−4,−3)$

إجابة: $y=−\frac{3}{2}x+9$

22. $m=−\frac{5}{2}$، نقطة$(−8,−2)$

23. $m=−7$، نقطة$(−1,−3)$

إجابة: $y=−7x−10$

24. $m=−4$، نقطة$(−2,−3)$

25. خط أفقي يحتوي على$(−2,5)$

إجابة: $y=5$

26. خط أفقي يحتوي على$(−2,−3)$

27. خط أفقي يحتوي على$(−1,−7)$

إجابة: $y=−7$

28. خط أفقي يحتوي على$(4,−8)$

أوجد معادلة الخط المستقيم بمعلومية نقطتين

في التمارين التالية، أوجد معادلة الخط الذي يحتوي على النقاط المُعطاة. اكتب المعادلة في صورة تقاطع منحدر.

29. $(2,6)$و$(5,3)$

إجابة: $y=−x+8$

30. $(4,3)$و$(8,1)$

31. $(−3,−4)$و$(5−2)$.

إجابة: $y=\frac{1}{4}x−\frac{13}{4}$

32. $(−5,−3)$و$(4,−6)$.

33. $(−1,3)$و$(−6,−7)$.

إجابة: $y=2x+5$

34. $(−2,8)$و$(−4,−6)$.

35. $(0,4)$و$(2,−3)$.

إجابة: $y=−\frac{7}{2}x+4$

36. $(0,−2)$و$(−5,−3)$.

37. $(7,2)$و$(7,−2)$.

إجابة: $x=7$

38. $(−2,1)$و$(−2,−4)$.

39. $(3,−4)$و$(5,−4)$.

إجابة: $y=−4$

40. $(−6,−3)$و$(−1,−3)$

ابحث عن معادلة الخط المستقيم الموازي لخط مُعطًى

في التمارين التالية، أوجد معادلة الخط المستقيم الموازي للخط المُعطى، ويحتوي على النقطة المُعطاة. اكتب المعادلة في صورة تقاطع منحدر.

41. خط$y=4x+2$، نقطة$(1,2)$

إجابة: $y=4x−2$

42. خط$y=−3x−1$، نقطة$2,−3)$.

43. السطر$2x−y=6$، النقطة$(3,0)$.

إجابة: $y=2x−6$

4. خط$2x+3y=6$، نقطة$(0,5)$.

45. خط$x=−4$، نقطة$(−3,−5)$.

إجابة: $x=−3$

46. خط$x−2=0$، نقطة$(1,−2)$

47. خط$y=5$، نقطة$(2,−2)$

إجابة: $y=−2$

48. خط$y+2=0$، نقطة$(3,−3)$

ابحث عن معادلة خط مستقيم عمودي على خط مُعطًى

في التمارين التالية، ابحث عن معادلة الخط المستقيم المتعامد على الخط المعطى وتحتوي على النقطة المُعطاة. اكتب المعادلة في صورة تقاطع منحدر.

49. خط$y=−2x+3$، نقطة$(2,2)$

إجابة: $y=\frac{1}{2}x+1$

50. خط$y=−x+5$، نقطة$(3,3)$

51. خط$y=\frac{3}{4}x−2$، نقطة$(−3,4)$

إجابة: $y=−\frac{4}{3}x$

52. خط$y=\frac{2}{3}x−4$، نقطة$(2,−4)$

5.3 خط$2x−3y=8$، نقطة$(4,−1)$

إجابة: $y=−\frac{3}{2}x+5$

54. خط$4x−3y=5$، نقطة$(−3,2)$

5. خط$2x+5y=6$، نقطة$(0,0)$

إجابة: $y=\frac{5}{2}x$

56. خط$4x+5y=−3$، نقطة$(0,0)$

57. خط$x=3$، نقطة$(3,4)$

إجابة: $y=4$

58. خط$x=−5$، نقطة$(1,−2)$

59. خط$x=7$، نقطة$(−3,−4)$

إجابة: $y=−4$

60. خط$x=−1$، نقطة$(−4,0)$

61. خط$y−3=0$، نقطة$(−2,−4)$

إجابة: $x=−2$

62. خط$y−6=0$، نقطة$(−5,−3)$

63. الخط$y$ - المحور، النقطة$(3,4)$

إجابة: $y=4$

64. الخط$y$ - المحور، النقطة$(2,1)$

ممارسة مختلطة

في التمارين التالية، ابحث عن معادلة كل سطر. اكتب المعادلة في صورة تقاطع منحدر.

65. تحتوي على النقاط$(4,3)$ و$(8,1)$

إجابة: $y=−\frac{1}{2}x+5$

66. تحتوي على النقاط$(−2,0)$ و$(−3,−2)$

67. $m=\frac{1}{6}$، تحتوي على نقطة$(6,1)$

إجابة: $y=\frac{1}{6}x$

68. $m=\frac{5}{6}$، تحتوي على نقطة$(6,7)$

69. بالتوازي مع الخط$4x+3y=6$، يحتوي على نقطة$(0,−3)$

إجابة: $y=−\frac{4}{3}x−3$

70. بالتوازي مع الخط$2x+3y=6$، يحتوي على نقطة$(0,5)$

71. $m=−\frac{3}{4}$، تحتوي على نقطة$(8,−5)$

إجابة: $y=−\frac{3}{4}x+1$

72. $m=−\frac{3}{5}$، تحتوي على نقطة$(10,−5)$

73. عمودي على الخط$y−1=0$، النقطة$(−2,6)$

إجابة: $x=−2$

74. عموديًا على الخط y - المحور، النقطة$(−6,2)$

75. بالتوازي مع الخط$x=−3$، يحتوي على نقطة$(−2,−1)$

إجابة: $x=−2$

76. بالتوازي مع الخط$x=−4$، يحتوي على نقطة$(−3,−5)$

77. تحتوي على النقاط$(−3,−4)$ و$(2,−5)$

إجابة: $y=−\frac{1}{5}x−\frac{23}{5}$

78. تحتوي على النقاط$(−5,−3)$ و$(4,−6)$

79. عمودي على الخط$x−2y=5$، النقطة$(−2,2)$

إجابة: $y=−2x−2$

80. عمودي على الخط$4x+3y=1$، النقطة$(0,0)$

تمارين الكتابة

81. لماذا تكون جميع الخطوط الأفقية متوازية؟

إجابة: سوف تتنوع الإجابات.

82. اشرح بكلماتك الخاصة لماذا يجب أن تحتوي منحدرات الخطين المتعامدين على علامات معاكسة.

فحص ذاتي

أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

$يوضِّح الشكل جدولاً يحتوي على ستة صفوف وأربعة أعمدة. الصف الأول عبارة عن صف العنوان ويقوم بتسمية كل عمود. عنوان العمود الأول هو «يمكنني...»، والثاني هو «بثقة»، والثالث هو «مع بعض المساعدة»، «لا ناقص لا أفهم ذلك!». تحت العمود الأول توجد عبارات «ابحث عن معادلة الخط بمعلومية المنحدر والجزء الصادي»، «ابحث عن معادلة الخط بمعلومية المنحدر والنقطة»، «ابحث عن معادلة الخط المعطى نقطتين»، «ابحث عن معادلة الخط الموازي لخط معين»، و «ابحث عن معادلة خط عمودي» إلى سطر معين». تحت الأعمدة الثانية والثالثة والرابعة توجد مساحات فارغة حيث يمكن للمتعلم التحقق من مستوى الإتقان الذي حققه.$

ب- ماذا تخبرك قائمة التحقق هذه عن إتقانك لهذا القسم؟ ما الخطوات التي ستتخذها للتحسين؟