3.4: ابحث عن معادلة الخط المستقيم
- Page ID
- 201396
في نهاية هذا القسم، ستكون قادرًا على:
- أوجد معادلة الخط المستقيم بمعلومية المنحدر والجزء المقطوع من محور الصادات
- أوجد معادلة الخط المستقيم بمعلومية المنحدر والنقطة
- أوجد معادلة الخط المستقيم بمعلومية نقطتين
- ابحث عن معادلة الخط المستقيم الموازي لخط مُعطًى
- ابحث عن معادلة خط مستقيم عمودي على خط مُعطًى
كيف تعرف الشركات عبر الإنترنت أنه «قد يعجبك أيضًا» عنصر معين بناءً على شيء طلبته للتو؟ كيف يمكن للاقتصاديين معرفة كيف سيؤثر ارتفاع الحد الأدنى للأجور على معدل البطالة؟ كيف يصنع الباحثون الطبيون أدوية لاستهداف الخلايا السرطانية؟ كيف يمكن لمهندسي المرور التنبؤ بتأثير زيادة أو نقصان أسعار الغاز على وقت التنقل؟ إنها كلها رياضيات.
تمتلئ العلوم الفيزيائية والعلوم الاجتماعية وعالم الأعمال بالحالات التي يمكن نمذجتها بمعادلات خطية تتعلق بمتغيرين. لإنشاء نموذج رياضي لعلاقة خطية بين متغيرين، يجب أن نكون قادرين على إيجاد معادلة الخط المستقيم. في هذا القسم، سننظر إلى عدة طرق لكتابة معادلة الخط. سيتم تحديد الطريقة المحددة التي نستخدمها من خلال المعلومات التي نقدمها.
أوجد معادلة الخط المستقيم بمعلومية المنحدر والجزء المقطوع من محور الصادات
يمكننا بسهولة تحديد ميل الخط وقطعه إذا كانت المعادلة مكتوبة في شكل منحدر\(y=mx+b\). الآن سنقوم بالعكس - سنبدأ بالمنحدر والتقاطع y ونستخدمهما لإيجاد معادلة الخط المستقيم.
أوجد معادلة الخط المستقيم الذي يحتوي على ميل\(−9\) ونقطة تقاطع y\((0,−4)\).
- إجابة
-
نظرًا لأننا نحصل على المنحدر والجزء الصادي للخط، يمكننا استبدال القيم المطلوبة في شكل تقاطع المنحدر،\(y=mx+b\).
قم بتسمية المنحدر. 
قم بتسمية y -Intercept. 
استبدل القيم بـ\(y=mx+b\). 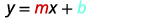
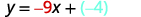
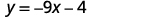
أوجد معادلة الخط المستقيم الذي يحتوي على ميل\(25\) ونقطة تقاطع y\((0,4)\).
- إجابة
-
\(y=\frac{2}{5}x+4\)
أوجد معادلة الخط المستقيم الذي يحتوي على ميل\(−1\) ونقطة تقاطع y\((0,−3)\).
- إجابة
-
\(y=−x−3\)
في بعض الأحيان، يجب تحديد المنحدر والاعتراض من الرسم البياني.
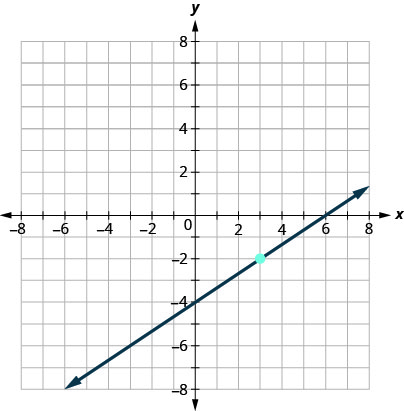
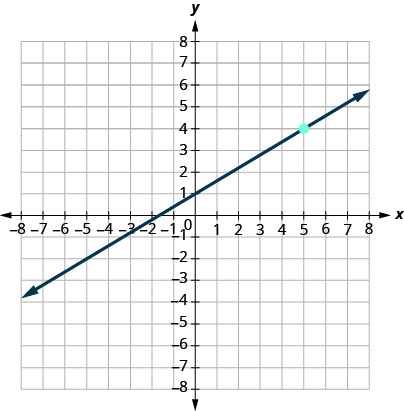
أوجد معادلة الخط الموضَّح في الرسم البياني.
- إجابة
-
نحتاج إلى إيجاد المنحدر والجزء المقطوع y للخط من الرسم البياني حتى نتمكن من استبدال القيم المطلوبة في نموذج التقاطع المنحدر\(y=mx+b\).
للعثور على المنحدر، نختار نقطتين على الرسم البياني.
التقاطع y هو\((0,−4)\) ويمر الرسم البياني من خلاله\((3,−2)\).
أوجد المنحدر، عن طريق حساب الارتفاع والجري. 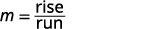

ابحث عن التقاطع y. 
استبدل القيم إلى y=mx+b.y=mx+b. 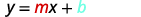
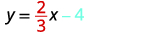
أوجد معادلة الخط الموضَّح في الرسم البياني.
- إجابة
-
\(y=\frac{3}{5}x+1\)
أوجد معادلة الخط الموضَّح في الرسم البياني.
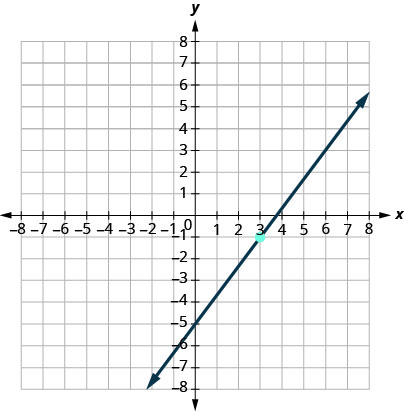
- إجابة
-
\(y=\frac{4}{3}x−5\)
أوجد معادلة الخط المستقيم بمعلومية الميل والنقطة
يعمل العثور على معادلة الخط باستخدام نموذج التقاطع المنحدر للمعادلة جيدًا عندما يتم إعطاؤك المنحدر والجزء المقطوع y أو عند قراءتهما من الرسم البياني. ولكن ماذا يحدث عندما يكون لديك نقطة أخرى بدلاً من التقاطع y؟
سنستخدم صيغة المنحدر لاشتقاق شكل آخر من معادلة الخط المستقيم.
لنفترض أن لدينا خطًا يحتوي على منحدر m ويحتوي على بعض النقاط المحددة\((x_1,y_1)\) وبعض النقاط الأخرى، والتي سنطلق عليها فقط\((x,y)\). يمكننا كتابة ميل هذا الخط ثم تغييره إلى شكل مختلف.
\( \begin{array} {llll} {} &{m} &= &{\frac{y-y_1}{x-x_1}} \\ {\text{Multiply both sides of the equation by }x−x_1.} &{m(x-x_1)} &= &{\left( \frac{y−y_1}{x−x_1} \right)(x−x_1)} \\ {\text{Simplify.}} &{m(x-x_1)} &= &{y-y_1} \\ {\text{Rewrite the equation with theyterms on the left.}} &{y-y_1} &= &{m(x-x_1)} \\ \end{array} \)
يُطلق على هذا التنسيق اسم نموذج نقطة المنحدر لمعادلة الخط.
شكل النقطة المنحدرة لمعادلة خط منحدر m ويحتوي على النقطة\((x_1,y_1)\) هو:
\[y−y_1=m(x−x_1) \nonumber\]
يمكننا استخدام صيغة النقطة المنحدرة للمعادلة لإيجاد معادلة الخط المستقيم عندما نعرف المنحدر ونقطة واحدة على الأقل. بعد ذلك، سنعيد كتابة المعادلة في صورة التقاطع المنحدر. تستخدم معظم تطبيقات المعادلات الخطية نموذج التقاطع المنحدر.
كيفية إيجاد معادلة خط مستقيم بمعلومية نقطة ومنحدر
ابحث عن معادلة الخط ذي المنحدر\(m=−\frac{1}{3}\) الذي يحتوي على النقطة\((6,−4)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-




أوجد معادلة الخط المستقيم الذي له ميل\(m=−\frac{2}{5}\) ويحتوي على النقطة\((10,−5)\).
- إجابة
-
\(y=−\frac{2}{5}x−1\)
أوجد معادلة الخط المستقيم الذي يحتوي على ميل\(m=−\frac{3}{4}\) ويحتوي على النقطة\((4,−7)\).
- إجابة
-
\(y=−\frac{3}{4}x−4\)
نسرد الخطوات للرجوع إليها بسهولة.
- حدد المنحدر.
- حدد النقطة.
- استبدل القيم في نموذج نقطة المنحدر،\(y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر.
ابحث عن معادلة الخط الأفقي الذي يحتوي على النقطة\((−2,−6)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
كل خط أفقي له ميل 0. يمكننا استبدال المنحدر والنقاط في شكل نقطة المنحدر،\(y−y_1=m(x−x1)\).
حدد المنحدر. 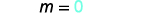
حدد النقطة. 
استبدل القيم بـ y−y1=m (x−x1) .y−y1=m (x−x1). 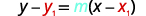
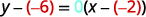
قم بالتبسيط. 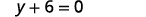
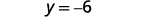
اكتب في شكل تقاطع منحدر. إنه في شكل y، ولكن يمكن كتابته\(y=0x−6\). هل وصلنا إلى شكل خط أفقي،\(y=a\)؟
أوجد معادلة الخط الأفقي الذي يحتوي على النقطة\((−3,8)\).
- إجابة
-
\(y=8\)
أوجد معادلة الخط الأفقي الذي يحتوي على النقطة\((−1,4)\).
- إجابة
-
\(y=4\)
أوجد معادلة الخط المستقيم بمعلومية نقطتين
عندما يتم جمع بيانات العالم الحقيقي، يمكن إنشاء نموذج خطي من نقطتي بيانات. في المثال التالي، سنرى كيفية العثور على معادلة الخط عند إعطاء نقطتين فقط.
حتى الآن، لدينا خياران لإيجاد معادلة الخط: تقاطع المنحدر أو النقطة المنحدرة. عندما نبدأ بنقطتين، يكون من المنطقي استخدام نموذج نقطة المنحدر.
ولكن بعد ذلك نحتاج إلى المنحدر. هل يمكننا إيجاد المنحدر بنقطتين فقط؟ نعم. بعد ذلك، عندما نحصل على المنحدر، يمكننا استخدامه وإحدى النقاط المعطاة لإيجاد المعادلة.
كيفية إيجاد معادلة الخط المستقيم بمعلومية نقطتين
ابحث عن معادلة الخط الذي يحتوي على النقاط\((−3,−1)\)\((2,−2)\) واكتب المعادلة في صورة مقطع منحدر.
- إجابة
-




ابحث عن معادلة الخط الذي يحتوي على النقاط\((−2,−4)\) و\((1,−3)\).
- إجابة
-
\(y=\frac{1}{3}x−\frac{10{3}\)
ابحث عن معادلة الخط الذي يحتوي على النقاط\((−4,−3)\) و\((1,−5)\).
- إجابة
-
\(y=−\frac{2}{5}x−\frac{23}{5}\)
يتم تلخيص الخطوات هنا.
- أوجد المنحدر باستخدام النقاط المُعطاة. \(m=\frac{y_2−y_1}{x_2−x_1}\)
- اختر نقطة واحدة.
- استبدل القيم في نموذج نقطة المنحدر:\(y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر.
ابحث عن معادلة الخط الذي يحتوي على النقاط\((−3,5)\) و\((−3,4)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
مرة أخرى، ستكون الخطوة الأولى هي العثور على المنحدر.
أوجد ميل الخط الذي يمر عبر\((−3,5)\) و\((−3,4)\).
\[m=\frac{y_2−y_1}{x_2−x_1} \nonumber\]
\[m=\frac{4−5}{−3−(−3)} \nonumber\]
\[m=\frac{−1}{0} \nonumber\]
المنحدر غير محدد.
هذا يخبرنا أنه خط عمودي. تحتوي كلتا النقطتين على إحداثيات x لـ\(−2\). إذن معادلتنا للخط هي\(x=−2\). نظرًا لعدم وجود y، لا يمكننا كتابته في شكل تقاطع منحدر.
قد ترغب في رسم رسم بياني باستخدام النقطتين المعنيتين. هل يتفق الرسم البياني الخاص بك مع استنتاجنا بأن هذا خط عمودي؟
ابحث عن معادلة الخط الذي يحتوي على النقاط\((5,1)\) و\((5,−4)\).
- إجابة
-
\(x=5\)
ابحث عن معادلة الخط الذي يحتوي على النقاط\((−4,4)\) و\((−4,3)\).
- إجابة
-
\(x=−4\)
لقد رأينا أنه يمكننا استخدام نموذج التقاطع المنحدر أو نموذج النقطة المنحدرة لإيجاد معادلة الخط المستقيم. يعتمد النموذج الذي نستخدمه على المعلومات التي نقدمها.
| لكتابة معادلة الخط المستقيم | ||
|---|---|---|
| إذا أعطيت: | استخدم: | النموذج: |
| المنحدر والجزء الصادي | اعتراض المنحدر | \(y=mx+b\) |
| منحدر ونقطة | نقطة المنحدر | \(y−y_1=m(x−x_1)\) |
| نقطتان | نقطة المنحدر | \(y−y_1=m(x−x_1)\) |
ابحث عن معادلة الخط المستقيم الموازي لخط مُعطًى
لنفترض أننا بحاجة إلى إيجاد معادلة لخط يمر بنقطة معينة ويوازي خطًا معينًا. يمكننا استخدام حقيقة أن الخطوط المتوازية لها نفس المنحدر. لذلك سيكون لدينا نقطة ومنحدر - فقط ما نحتاجه لاستخدام معادلة النقطة والمنحدر.
أولاً، دعونا ننظر إلى هذا بيانياً.
يوضح هذا الرسم البياني\(y=2x−3.\) أننا نريد رسم خط موازٍ لهذا الخط ويمر عبر النقطة\((−2,1)\).
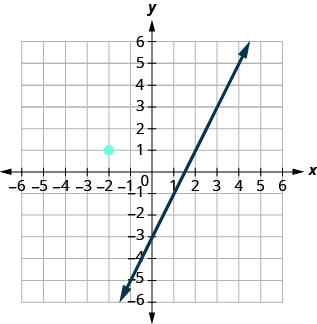
نحن نعلم أن الخطوط المتوازية لها نفس المنحدر. لذلك سيكون للخط الثاني نفس المنحدر\(y=2x−3\). هذا المنحدر هو\(m_∥=2\). سنستخدم الترميز mmلتمثيل ميل الخط الموازي للخط ذي المنحدر m. (لاحظ أن النص البرمجي || يشبه سطرين متوازيين.)
سوف يمر الخط الثاني\((−2,1)\) ويكون\(m=2\).
لرسم الخط، نبدأ عند\((−2,1)\) الارتفاع والجري ونحسب.
مع\(m=2\) (أو\(m=\frac{2}{1}\))، نحسب الارتفاع 2 والركض 1. نرسم الخط، كما هو موضح في الرسم البياني.
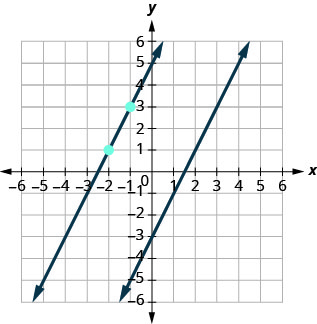
هل تظهر الخطوط متوازية؟ هل يمر الخط الثاني\((−2,1)\)؟
لقد طُلب منا رسم الخط، والآن دعونا نرى كيفية القيام بذلك جبريًا.
يمكننا استخدام نموذج التقاطع المنحدر أو نموذج النقطة المنحدرة لإيجاد معادلة الخط المستقيم. هنا نعرف نقطة واحدة ويمكننا العثور على المنحدر. لذلك سوف نستخدم نموذج نقطة المنحدر.
كيفية إيجاد معادلة الخط المستقيم الموازي لخط معين ونقطة
ابحث عن معادلة الخط الموازي للخط\(y=2x−3\) الذي يحتوي على النقطة\((−2,1)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
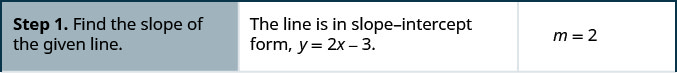




انظر إلى الرسم البياني مع الخطوط المتوازية الموضحة سابقًا. هل هذه المعادلة منطقية؟ ما التقاطع y للخط؟ ما هو المنحدر؟
ابحث عن معادلة الخط الموازي للخط\(y=3x+1\) الذي يحتوي على النقطة\((4,2)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(y=3x−10\)
ابحث عن معادلة الخط الموازي للخط\(y=12x−3\) الذي يحتوي على النقطة\((6,4)\).
اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(y=\frac{1}{2}x+1\)
- أوجد ميل الخط المُعطى.
- أوجد ميل الخط الموازي.
- حدد النقطة.
- استبدل القيم في نموذج نقطة المنحدر:\(y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر.
ابحث عن معادلة خط مستقيم عمودي على خط مُعطًى
الآن، دعونا ننظر في الخطوط العمودية. لنفترض أننا بحاجة إلى إيجاد خط يمر بنقطة معينة ويكون عموديًا على خط معين. يمكننا استخدام حقيقة أن الخطوط العمودية لها منحدرات تمثل تبادلات سالبة. سنستخدم مرة أخرى معادلة نقطة المنحدر، كما فعلنا مع الخطوط المتوازية.
يوضح هذا الرسم البياني\(y=2x−3\). الآن، نريد رسم خط عمودي على هذا الخط ويمر عبره\((−2,1)\).
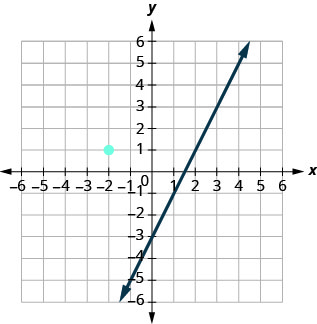
نحن نعلم أن الخطوط العمودية لها منحدرات تمثل تبادلات سالبة.
سنستخدم الترميز\(m_⊥\) لتمثيل ميل الخط العمودي على الخط ذي المنحدر m. (لاحظ أن الحرف السفلي\(⊥\) يشبه الزوايا اليمنى المكونة من خطين عموديين.)
\[y=2x−3 perpendicular line \nonumber\]
\[m=2 m⊥=−12\nonumber\]
نحن نعلم الآن أن الخط العمودي سيمر\((−2,1)\) بـ\(m⊥=−12\).
لرسم الخط، سنبدأ عند\((−2,1)\) الارتفاع والارتفاع\(−1\) ونحسب\(2\). ثم نرسم الخط.
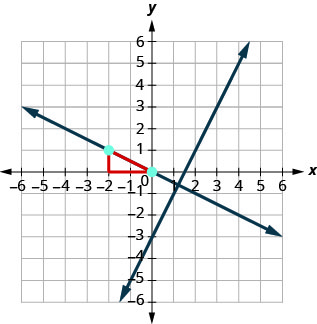
هل تظهر الخطوط بشكل عمودي؟ هل يمر الخط الثاني\((−2,1)\)؟
طُلب منا رسم الخط، الآن، دعونا نرى كيفية القيام بذلك جبريًا.
يمكننا استخدام نموذج التقاطع المنحدر أو نموذج النقطة المنحدرة لإيجاد معادلة الخط المستقيم. في هذا المثال، نعرف نقطة واحدة، ويمكننا العثور على المنحدر، لذلك سنستخدم نموذج نقطة المنحدر.
كيفية إيجاد معادلة الخط المستقيم العمودي على خط معين ونقطة
ابحث عن معادلة الخط المستقيم العمودي\(y=2x−3\) الذي يحتوي على النقطة\((−2,1)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-





ابحث عن معادلة الخط المستقيم العمودي على الخط\(y=3x+1\) الذي يحتوي على النقطة\((4,2)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(y=−\frac{1}{3}x+\frac{10}{3}\)
ابحث عن معادلة الخط المستقيم العمودي على الخط\(y=12x−3\) الذي يحتوي على النقطة\((6,4)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(y=−2x+16\)
- أوجد ميل الخط المُعطى.
- أوجد ميل الخط العمودي.
- حدد النقطة.
- استبدل القيم في نموذج نقطة المنحدر،\(y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر.
ابحث عن معادلة الخط المستقيم العمودي\(x=5\) الذي يحتوي على النقطة\((3,−2)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
مرة أخرى، نظرًا لأننا نعرف نقطة واحدة، يبدو خيار النقطة والمنحدر واعدًا أكثر من خيار اعتراض المنحدر. نحتاج إلى المنحدر لاستخدام هذا النموذج، ونعلم أن الخط الجديد سيكون عموديًا على x=5.x=5. هذا الخط عمودي، لذا سيكون عموده أفقيًا. هذا يخبرنا m=0.m=0.
حدد النقطة. حدد ميل الخط العمودي. استبدل القيم بـ −y1=m (x−x1) .قم بالتبسيط. (3، −2) my−y1y− (−2) y+2y====0m (x−x1) 0 (x−3) 0−2حدد النقطة. (3, −2) حدد ميل الخط العمودي. استبدل القيم بـ y−y1=m (x−x1) .التبسيط.m= 0Y−Y1=م (x−x1) − (−2) = 0 (x−3) y+2=0y=−2
ارسم الرسم البياني لكلا الخطين. في الرسم البياني الخاص بك، هل تبدو الخطوط متعامدة؟
ابحث عن معادلة الخط المستقيم المتعامد مع الخط\(x=4\) الذي يحتوي على النقطة\((4,−5)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(y=−5\)
ابحث عن معادلة الخط المستقيم المتعامد مع الخط\(x=2\) الذي يحتوي على النقطة\((2,−1)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(y=−1\)
على سبيل المثال، استخدمنا نموذج النقطة المنحدرة لإيجاد المعادلة. كان بإمكاننا النظر إلى هذا بطريقة مختلفة.
نريد أن نجد خطًا متعامدًا مع الخط\(x=5\) الذي يحتوي على النقطة\((3,−2)\). يوضح لنا هذا الرسم البياني الخط\(x=5\) والنقطة\((3,−2)\).
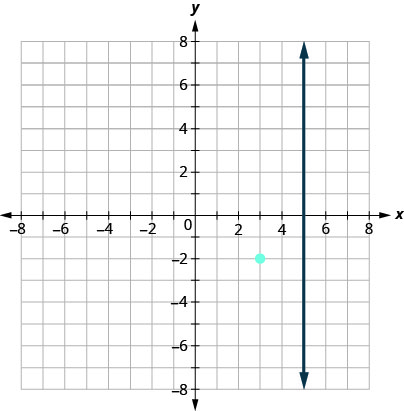
نحن نعلم أن كل خط عمودي على خط عمودي أفقي، لذلك سنقوم برسم الخط الأفقي من خلاله\((3,−2)\).
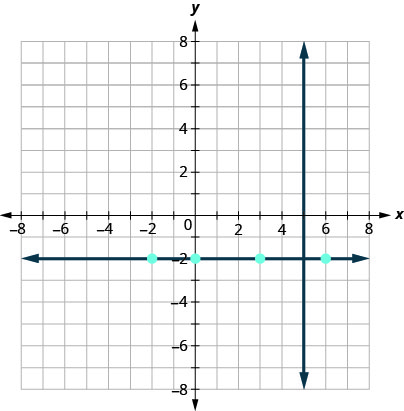
هل تظهر الخطوط بشكل عمودي؟
إذا نظرنا إلى بضع نقاط على هذا الخط الأفقي، نلاحظ أن جميعها تحتوي على إحداثيات y لـ\(−2\). إذن، معادلة الخط العمودي على الخط العمودي\(x=5\) هي\(y=−2\).
ابحث عن معادلة الخط المستقيم العمودي\(y=−3\) الذي يحتوي على النقطة\((−3,5)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
الخط\(y=−3\) هو خط أفقي. يجب أن يكون أي خط عمودي عليه عموديًا في النموذج\(x=a\). نظرًا لأن الخط العمودي عمودي ويمر عبره\((−3,5)\)، فإن كل نقطة عليه لها إحداثيات x x\(−3\). معادلة الخط العمودي هي\(x=−3\).
قد ترغب في رسم الخطوط. هل تظهر بشكل عمودي؟
ابحث عن معادلة الخط المستقيم المتعامد مع الخط\(y=1\) الذي يحتوي على النقطة\((−5,1)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(x=−5\)
ابحث عن معادلة الخط المستقيم المتعامد مع الخط\(y=−5\) الذي يحتوي على النقطة\((−4,−5)\). اكتب المعادلة في صورة تقاطع منحدر.
- إجابة
-
\(x=−4\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة للعثور على معادلة الخط.
المفاهيم الرئيسية
- كيفية إيجاد معادلة خط مستقيم بمعلومية المنحدر والنقطة.
- حدد المنحدر.
- حدد النقطة.
- استبدل القيم في نموذج نقطة المنحدر،\( y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر.
- كيفية إيجاد معادلة خط مستقيم بمعلومية نقطتين.
- أوجد المنحدر باستخدام النقاط المُعطاة. \(m=\frac{y_2−y_1}{x_2−x_1}\)
- اختر نقطة واحدة.
- استبدل القيم في نموذج نقطة المنحدر:\(y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر.
لكتابة معادلة الخط المستقيم إذا أعطيت: استخدم: النموذج: المنحدر والجزء الصادي اعتراض المنحدر \(y=mx+b\) منحدر ونقطة نقطة المنحدر \(y−y_1=m(x−x_1)\) نقطتان نقطة المنحدر \(y−y_1=m(x−x_1)\)
- كيفية إيجاد معادلة خط موازي لخط معين.
- أوجد ميل الخط المُعطى.
- أوجد ميل الخط الموازي.
- حدد النقطة.
- استبدل القيم في نموذج نقطة المنحدر:\(y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر
- كيفية إيجاد معادلة خط عمودي على خط معين.
- أوجد ميل الخط المُعطى.
- أوجد ميل الخط العمودي.
- حدد النقطة.
- استبدل القيم في نموذج نقطة المنحدر،\(y−y_1=m(x−x_1)\).
- اكتب المعادلة في صورة تقاطع منحدر.
مسرد المصطلحات
شكل نقطة المنحدر
شكل النقطة المنحدرة لمعادلة خط منحدر m ويحتوي على النقطة\((x_1,y_1)\) هو\(y−y_1=m(x−x_1)\).


