3.3E: تمارين

Last updated
Save as PDF

Page ID: 201409

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

الممارسة تجعل من الكمال

أوجد ميل الخط المستقيم

في التمارين التالية، أوجد ميل كل خط موضَّح.

1.
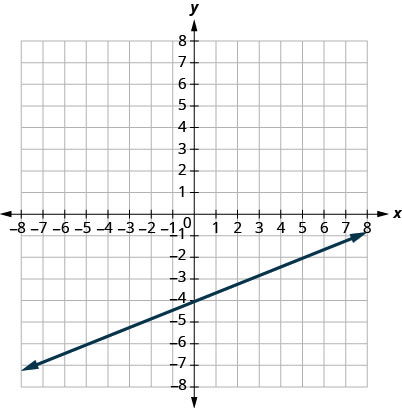
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، سالب 4) و (5، سالب 2).$

إجابة: $m=\frac{2}{5}$

2.
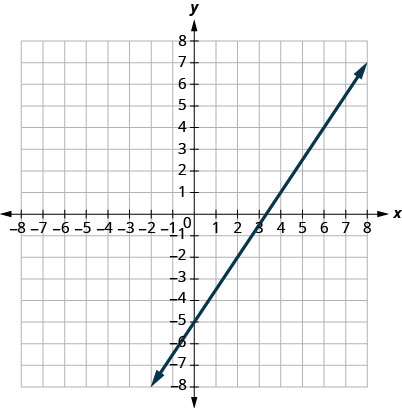
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، سالب 5) و (2، سالب 2).$

3.
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، سالب 1) و (4، 4).$

إجابة: $m=\frac{5}{4}$

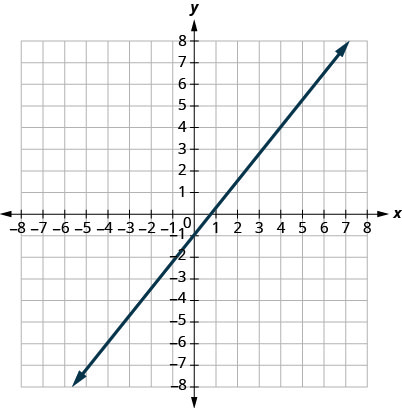
4.
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، سالب 2) و (3، 3).$

5.
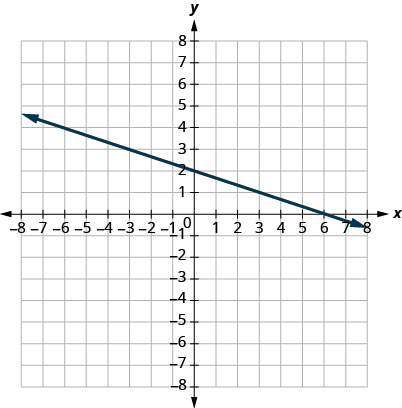
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، 2) و (3، 1).$

إجابة: $m = -\frac{1}{3}$

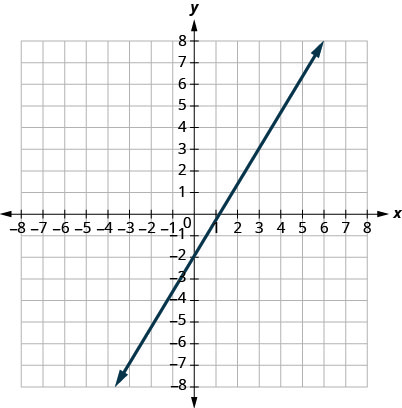
6.
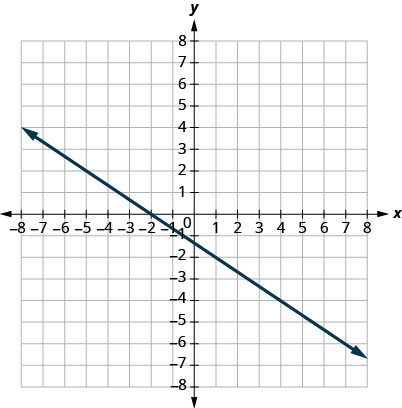
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، سالب 1) و (3، سالب 3).$

7.
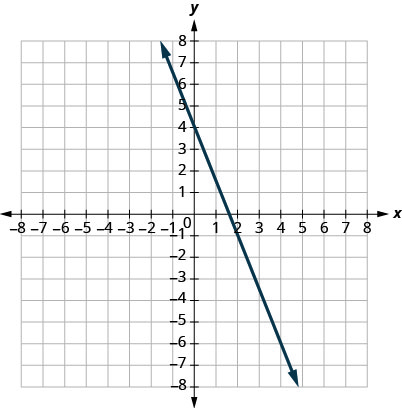
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، 4) و (2، سالب 1).$

إجابة: $m = -\frac{5}{2}$

8.
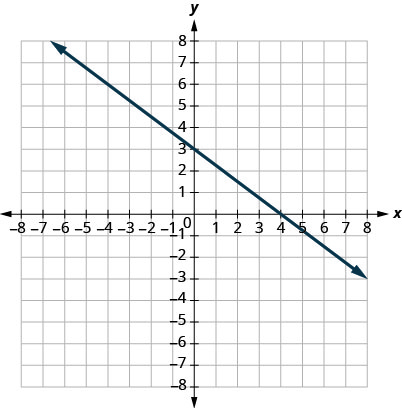
$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 8 إلى 8. يمتد المحور y من سالب 8 إلى 8. يمر الخط بالنقاط (0، 2) و (4، سالب 1).$

في التمارين التالية، ابحث عن ميل كل خط.

9. $y=3$

إجابة: $m = 0$

10. $y=−2$

11. $x=−5$

إجابة: غير محدد

12. $x=4$

في التمارين التالية، استخدم صيغة المنحدر للعثور على ميل الخط الفاصل بين كل زوج من النقاط.

13. $(2,5),\;(4,0)$

إجابة: $m = -\frac{5}{2}$

14. $(3,6),\;(8,0)$

15. $(−3,3),\;(4,−5)$

إجابة: $m = -\frac{8}{7}$

16. $(−2,4),\;(3,−1)$

17. $(−1,−2),\;(2,5)$

إجابة: $m = \frac{7}{3}$

18. $(−2,−1),\;(6,5)$

19. $(4,−5),\;(1,−2)$

إجابة: $m = -1$

20. $(3,−6),\;(2,−2)$

رسم بياني للخط المستقيم بمعلومية النقطة والمنحدر

في التمارين التالية، قم برسم بياني لكل خط بالنقطة والمنحدر الموضحين.

21. $(2,5)$؛$m=−\frac{1}{3}$

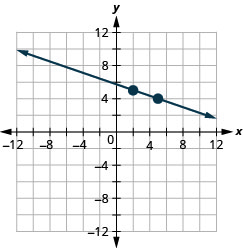
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 12 إلى 12. يمتد المحور y من سالب 12 إلى 12. يمر الخط بالنقاط (2، 5) و (5، 4).$

22. $(1,4)$؛$m=−\frac{1}{2}$

23. $(−1,−4)$؛$m=\frac{4}{3}$

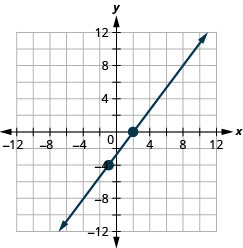
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 12 إلى 12. يمتد المحور y من سالب 12 إلى 12. يمر الخط بالنقاط (سالب 1، سالب 4) و (2، 0).$

24. $(−3,−5)$؛$m=\frac{3}{2}$

25. $y$- الاعتراض:$(0, 3)$؛$m=−\frac{2}{5}$

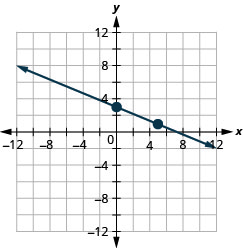
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 12 إلى 12. يمتد المحور y من سالب 12 إلى 12. يمر الخط بالنقاط (0، 3) و (5، 1).$

26. $x$- الاعتراض:$(−2,0)$؛$m=\frac{3}{4}$

27. $(−4,2)$؛$m=4$

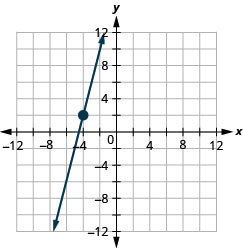
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 12 إلى 12. يمتد المحور y من سالب 12 إلى 12. يمر الخط بالنقاط (سالب 4، 2) و (سالب 3، 6).$

28. $(1,5)$؛$m=−3$

رسم خط مستقيم باستخدام ميله والجزء المقطوع منه

في التمارين التالية، حدد المنحدر والجزء المقطوع y لكل خط.

29. $y=−7x+3$

إجابة: $m=−7$؛$(0,3)$

30. $y=4x−10$

31. $3x+y=5$

إجابة: $m=−3$؛$(0,5)$

32. $4x+y=8$

33. $6x+4y=12$

إجابة: $m=−\frac{3}{2}$؛$(0,3)$

34. $8x+3y=12$

35. $5x−2y=6$

إجابة: $m=\frac{5}{2}$؛$(0,−3)$

36. $7x−3y=9$

في التمارين التالية، قم برسم خط كل معادلة بيانيًا باستخدام المنحدر والجزء المقطوع من y.

37. $y=3x−1$

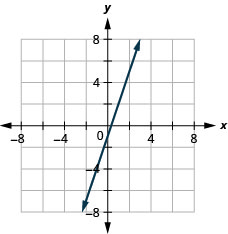
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 10 إلى 10. يمتد المحور y من سالب 10 إلى 10. يمر الخط بالنقاط (0، سالب 1) و (1، 2).$

38. $y=2x−3$

39. $y=−x+3$

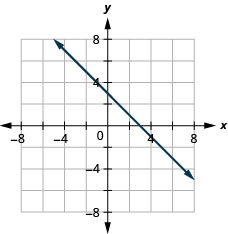
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 10 إلى 10. يمتد المحور y من سالب 10 إلى 10. يمر الخط بالنقاط (0، 3) و (1، 2).$

40. $y=−x−4$

41. $y=−\frac{2}{5}x−3$

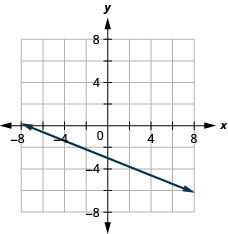
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 10 إلى 10. يمتد المحور y من سالب 10 إلى 10. يمر الخط بالنقاط (0، سالب 3) و (5، سالب 5).$

42. $y=−\frac{3}{5}x+2$

43. $3x−2y=4$

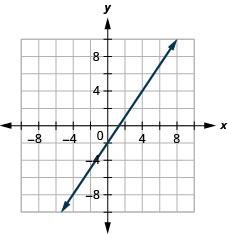
إجابة: $يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 10 إلى 10. يمتد المحور y من سالب 10 إلى 10. يمر الخط بالنقاط (0، سالب 2) و (2، 1).$

44. $3x−4y=8$

اختر الطريقة الأكثر ملاءمة لرسم خط

في التمارين التالية، حدد الطريقة الأكثر ملاءمة لرسم كل سطر.

45. $x=2$

إجابة: خط عمودي

46. $y=5$

47. $y=−3x+4$

إجابة: اعتراض المنحدر

48. $x−y=5$

49. $x−y=1$

إجابة: عمليات الاعتراض

50. $y=\frac{2}{3}x−1$

51. $3x−2y=−12$

إجابة: عمليات الاعتراض

52. $2x−5y=−10$

رسم بياني وتفسير تطبيقات المنحدر — التقاطع

53. $P=31+1.75w$تُمثِّل المعادلة العلاقة بين مبلغ فاتورة المياه الشهرية لشركة Tuyet بالدولار وعدد وحدات المياه المستخدمة.$P$$w$

أ- ابحث عن مدفوعات Tuyet لمدة شهر عند استخدام$0$ وحدات المياه.

ب- ابحث عن مدفوعات Tuyet لمدة شهر عند استخدام$12$ وحدات المياه.

ج. قم بتفسير ميل المعادلة$P$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

إجابة

أ.$$31$
ب.$$52$
ج. المنحدر$1.75$، يعني أن الدفعة$$1.75$ تزداد بمقدار زيادة عدد وحدات المياه المستخدمة بمقدار$1$.$P$$w$ يعني التقاطع$P$ -Intercept أنه عندما يكون عدد وحدات المياه المستخدمة هو$0$ Tuyet، يتم الدفع$$31$.
د.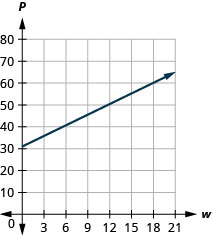

$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 1 إلى 21. يمتد المحور y من سالب 1 إلى 80. يمر الخط بالنقاط (0، 31) و (12، 52).$

54. $P=28+2.54w$تُمثِّل المعادلة العلاقة بين مبلغ فاتورة المياه الشهرية لراندي بالدولار وعدد وحدات المياه المستخدمة.$P$$w$

أ- ابحث عن الدفعة لمدة شهر عندما استخدم راندي$0$ وحدات المياه.

ب- ابحث عن الدفعة لمدة شهر عندما استخدم راندي$15$ وحدات المياه.

ج. قم بتفسير ميل المعادلة$P$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

55. يقود بروس سيارته من أجل وظيفته. $R=0.575m+42$تُمثل المعادلة العلاقة بين المبلغ بالدولار$R$، الذي يتم تعويضه وعدد الأميال التي يقودها في يوم واحد.$m$

أ- ابحث عن المبلغ الذي يتم تعويضه عن بروس في اليوم الذي يقود فيه$0$ الأميال.

ب- ابحث عن المبلغ الذي يتم تعويضه عن بروس في اليوم الذي يقود فيه$220$ الأميال.

ج. قم بتفسير ميل المعادلة$R$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

إجابة

أ.$$42$
ب.$$168.50$
ج. المنحدر،$0.575$ يعني أن المبلغ الذي يتم تعويضه$R$، يزداد$$0.575$ عندما يزداد عدد الأميال المقطوعة$m$، بمقدار$1$. يعني$R$ التقاطع -incept أنه عندما يكون عدد الأميال المقطوعة$0$، يكون المبلغ الذي يتم تعويضه$$42$.
د.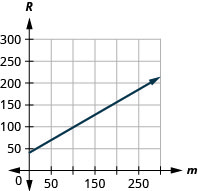

$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 50 إلى 250. يمتد المحور y من سالب 50 إلى 300. يمر الخط بالنقاط (0، 42) و (220، 168.5).$

56. تخطط جانيل لاستئجار سيارة أثناء إجازتها. تمثل$C=0.32m+15$ المعادلة العلاقة بين التكلفة بالدولار$C$، في اليوم وعدد الأميال$m$، وتقودها في يوم واحد.

أ- ابحث عن التكلفة في حالة قيادة جانيل$0$ لأميال السيارة في يوم واحد.

ب- ابحث عن التكلفة في اليوم الذي تقود فيه جانيل السيارة$400$ لأميال.

ج. قم بتفسير ميل المعادلة$C$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

57. تعمل شيري في البيع بالتجزئة ويشمل راتبها الأسبوعي عمولة على المبلغ الذي تبيعه. $S=400+0.15c$تُمثل المعادلة العلاقة بين راتبها الأسبوعي بالدولار ومقدار مبيعاتها بالدولار.$S$$c$

أ- ابحث عن راتب شيري لمدة أسبوع عندما كانت مبيعاتها$$0$.

ب- ابحث عن راتب شيري لمدة أسبوع عندما كانت مبيعاتها$$3,600$.

ج. قم بتفسير ميل المعادلة$S$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

إجابة

أ.$$400$
ب.$$940$
ج. المنحدر$0.15$، يعني أن راتب شيري، S، يزيد$$0.15$ بنسبة لكل$$1$ زيادة في مبيعاتها. $S$الاعتراض يعني أنه عندما تكون مبيعاتها$$0$، يكون راتبها$$400$.
د.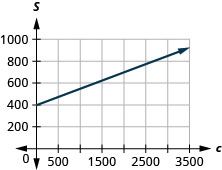

$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 500 إلى 3500. يمتد المحور y من سالب 200 إلى 1000. يمر الخط بالنقاط (0، 400) و (3600، 940).$

58. يشمل الراتب الأسبوعي لباتيل الأجر الأساسي بالإضافة إلى العمولة على مبيعاته. $S=750+0.09c$تُمثل المعادلة العلاقة بين راتبه الأسبوعي بالدولار ومقدار مبيعاته بالدولار.$S$$c$

أ- ابحث عن راتب باتيل لمدة أسبوع عندما كانت مبيعاته$0$.

ب- ابحث عن راتب باتيل لمدة أسبوع عندما كانت مبيعاته$18,540$.

ج. قم بتفسير ميل المعادلة$S$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

59. تخطط كوستا لمأدبة غداء. $C=450+28g$تُمثل المعادلة العلاقة بين تكلفة$C$ المأدبة بالدولار وعدد الضيوف$g$.

أ- ابحث عن التكلفة إذا كان عدد الضيوف هو$40$.

ب- ابحث عن التكلفة إذا كان عدد الضيوف هو$80$.

ج. قم بتفسير ميل المعادلة$C$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

إجابة

أ.$$1570$
ب.$$5690$
ج. يعطي المنحدر التكلفة لكل ضيف. المنحدر$28$، يعني أن التكلفة$C$، تزداد$$28$ عندما يزداد عدد الضيوف بمقدار$1$. يعني$C$ الاعتراض -Intercept أنه إذا كان عدد الضيوف$0$، فستكون التكلفة$$450$.
د.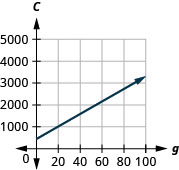

$يوضِّح هذا الشكل التمثيل البياني لخط مستقيم على المستوى الإحداثي x y. يمتد المحور السيني من سالب 20 إلى 100. يمتد المحور y من سالب 1000 إلى 7000. يمر الخط بالنقاط (0، 450) و (40، 1570).$

60. تخطط مارجي لمأدبة عشاء. $C=750+42g$تُمثل المعادلة العلاقة بين تكلفة$C$ المأدبة بالدولار وعدد الضيوف$g$.

أ- ابحث عن التكلفة إذا كان عدد الضيوف هو$50$.

ب- ابحث عن التكلفة إذا كان عدد الضيوف هو$100$.

ج. قم بتفسير ميل المعادلة$C$ والجزء المقطوع منها.

د. رسم المعادلة بيانيًا.

استخدم المنحدرات لتحديد الخطوط المستقيمة المتوازية والمتعامدة

في التمارين التالية، استخدم المنحدرات$y$ ونقاط التقاطع لتحديد ما إذا كانت الخطوط متوازية أو عمودية أم لا.

61. $y=\frac{3}{4}x−3$؛$3x−4y=−2$

إجابة: موازى

62. $3x−4y=−2$؛$y=\frac{3}{4}x−3$

63. $2x−4y=6$؛$x−2y=3$

إجابة: ولا

64. $8x+6y=6$؛$12x+9y=12$

65. $x=5$؛$x=−6$

إجابة: موازى

66. $x=−3$؛$x=−2$

67. $4x−2y=5$؛$3x+6y=8$

إجابة: عمودي

68. $8x−2y=7$؛$3x+12y=9$

69. $3x−6y=12$؛$6x−3y=3$

إجابة: ولا

70. $9x−5y=4$؛$5x+9y=−1$

71. $7x−4y=8$؛$4x+7y=14$

إجابة: عمودي

72. $5x−2y=11$؛$5x−y=7$

73. $3x−2y=8$؛$2x+3y=6$

إجابة: عمودي

74. $2x+3y=5$؛$3x−2y=7$

75. $3x−2y=1$؛$2x−3y=2$

إجابة: ولا

76. $2x+4y=3$؛$6x+3y=2$

77. $y=2$؛$y=6$

إجابة: موازى

78. $y=−1$؛$y=2$

تمارين الكتابة

79. كيف$m=12$ يختلف الرسم البياني للخط ذي المنحدر عن الرسم البياني للخط ذي المنحدر$m=2$؟

إجابة: سوف تتنوع الإجابات.

80. لماذا يكون منحدر الخط العمودي «غير محدد»؟

81. اشرح كيف يمكنك رسم خط بمعلومية نقطة ومنحدره.

إجابة: سوف تتنوع الإجابات.

82. اشرح بكلماتك الخاصة كيفية تحديد الطريقة التي يجب استخدامها لرسم خط.

فحص ذاتي

أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

$يحتوي هذا الجدول على 7 صفوف و 4 أعمدة. الصف الأول عبارة عن صف العنوان ويقوم بتسمية كل عمود. عنوان العمود الأول هو «يمكنني...»، والثاني هو «بثقة»، والثالث هو «مع بعض المساعدة»، والرابع هو «لا، لا أفهم ذلك». تحت العمود الأول توجد عبارات «العثور على منحدر الخط»، و «رسم خط بياني بنقطة ومنحدر»، و «رسم خطًا باستخدام ميله واعتراضه»، و «اختر الطريقة الأكثر ملاءمة لرسم خط»، و «رسم بياني وتفسير تطبيقات التقاطع المنحدر»، و «استخدام المنحدرات لتحديد الموازي و خطوط عمودية». يتم ترك الأعمدة الأخرى فارغة حتى يتمكن المتعلم من تحديد مستوى إتقانه لكل موضوع.$

ب- بعد مراجعة قائمة التحقق هذه، ماذا ستفعل لتصبح واثقًا من جميع الأهداف؟