3.3: ميل الخط

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• أوجد ميل الخط
• رسم بياني لخط بمعلومية النقطة والمنحدر
• ارسم خطًا بيانيًا باستخدام المنحدر والفاصل
• اختر الطريقة الأكثر ملاءمة لرسم خط
• رسم تطبيقات المنحدر-التقاطع وتفسيرها
• استخدم المنحدرات لتحديد الخطوط المتوازية والعمودية

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. قم بالتبسيط:$\frac{(1–4)}{(8−2)}$.
   إذا فاتتك هذه المشكلة، راجع [link].
2. قسّم:$\frac{0}{4}$,$\frac{4}{0}$.
   إذا فاتتك هذه المشكلة، راجع [link].
3. تبسيط:$\frac{15}{-3}$،$\frac{-15}{3}$،$\frac{-15}{-3}$.
   إذا فاتتك هذه المشكلة، راجع [link].

أوجد ميل الخط المستقيم

عندما تقوم برسم المعادلات الخطية بيانيًا، قد تلاحظ أن بعض الخطوط تميل لأعلى أثناء انتقالها من اليسار إلى اليمين وبعض الخطوط تميل لأسفل. بعض الخطوط شديدة الانحدار وبعض الخطوط مسطحة.

في الرياضيات، يُطلق على قياس انحدار الخط اسم منحدر الخط.

لمفهوم المنحدر العديد من التطبيقات في العالم الحقيقي. في البناء، تعتبر أرضية السقف، وميل أنابيب السباكة، وانحدار السلالم كلها تطبيقات للانحدار. وأثناء التزلج أو الركض أسفل التل، ستشعر بالتأكيد بالانحدار.

يمكننا تعيين قيمة عددية لمنحدر الخط من خلال إيجاد نسبة الارتفاع والجري. الارتفاع هو المقدار الذي تتغير فيه المسافة الرأسية بينما يقيس الجري التغيير الأفقي، كما هو موضح في هذا الرسم التوضيحي. المنحدر هو معدل التغيير. انظر الشكل.

الشكل$\PageIndex{1}$.

ميل الخط

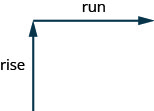
منحدر الخط هو$m=\frac{\text{rise}}{\text{run}}$.

يقيس الارتفاع التغيير الرأسي ويقيس الجري التغيير الأفقي.

للعثور على ميل الخط، نحدد نقطتين على الخط الذي تكون إحداثياته عبارة عن أعداد صحيحة. ثم نرسم مثلثًا قائمًا حيث تكون النقطتان عبارة عن رءوس وجانب واحد أفقي وجانب واحد عمودي.

للعثور على منحدر الخط، نقيس المسافة على طول الجوانب الرأسية والأفقية للمثلث. تسمى المسافة الرأسية بالارتفاع والمسافة الأفقية تسمى الجري،

أوجد ميل الخط المستقيم من رسمه البياني باستخدام$m=\frac{\text{rise}}{\text{run}}$

1. حدد موقع نقطتين على الخط الذي تكون إحداثياته عبارة عن أعداد صحيحة.
2. بدءًا من نقطة واحدة، ارسم مثلثًا قائمًا، بدءًا من النقطة الأولى إلى النقطة الثانية.
3. احسب الارتفاع والجري على أرجل المثلث.
4. خذ نسبة الارتفاع للركض للعثور على المنحدر:$m=\frac{\text{rise}}{\text{run}}$.

مثال$\PageIndex{1}$

أوجد ميل الخط المستقيم الموضح.

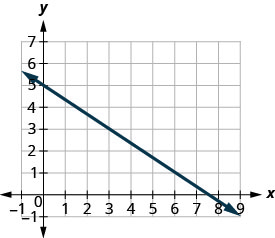
إجابة

حدد نقطتين على الرسم البياني التي تكون إحداثياتها عبارة عن أعداد صحيحة.	$(0,5)$و$(3,3)$
بدءًا من$(0,5)$، ارسم مثلثًا قائمًا $(3,3)$ كما هو موضح في هذا الرسم البياني.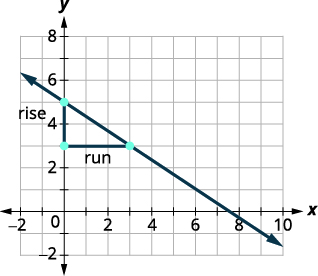
أحسب الارتفاع — بما أنه ينخفض، فهو سلبي.	الارتفاع هو$−2$.
عد الجري.	الجري هو 3.
استخدم صيغة المنحدر.	$m=\frac{\text{rise}}{\text{run}}$
استبدل قيم الصعود والجري.	$m=−23$
قم بالتبسيط.	$m=−23$
	منحدر الخط هو$−23$.
	لذلك تنخفض y بمقدار وحدتين مع زيادة x بمقدار 3 وحدات.

مثال$\PageIndex{2}$

أوجد ميل الخط المستقيم الموضح.

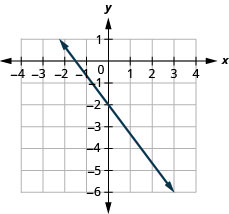
إجابة

$-\frac{4}{3}$

مثال$\PageIndex{3}$

أوجد ميل الخط المستقيم الموضح.

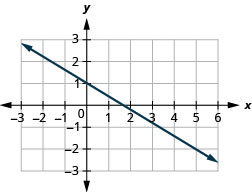
إجابة

$-\frac{3}{5}$

كيف نجد منحدر الخطوط الأفقية والعمودية؟ لإيجاد ميل الخط الأفقي$y=4$، يمكننا رسم الخط بيانيًا، وإيجاد نقطتين عليه، وحساب الارتفاع والجري. دعونا نرى ما يحدث عندما نفعل ذلك، كما هو موضح في الرسم البياني أدناه.

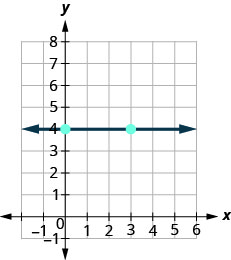
$\begin{array} {ll} {\text{What is the rise?}} &{\text{The rise is }0.} \\ {\text{What is the run?}} &{\text{The run is }3.} \\ {\text{What is the slope?}} &{m=\frac{\text{rise}}{\text{run}}} \\ {} &{m=\frac{0}{3}} \\ {} &{m=0} \\{}&{\text{The slope of the horizontal line } y=4 \text{ is }0.} \\ \end{array} \nonumber$

لننظر أيضًا في الخط العمودي، الخط$x=3$، كما هو موضح في الرسم البياني.

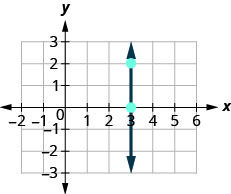
$\begin{array} {ll} {\text{What is the rise?}} &{\text{The rise is }0.} \\ {\text{What is the run?}} &{\text{The run is }3.} \\ {\text{What is the slope?}} &{m=\frac{\text{rise}}{\text{run}}} \\ {} &{m=\frac{2}{0}} \\ \end{array} \nonumber$

المنحدر غير محدد لأن القسمة على الصفر غير محددة. لذلك نقول أن منحدر الخط العمودي$x=3$ غير محدد.

تحتوي جميع الخطوط الأفقية على منحدر 0. عندما تكون إحداثيات y هي نفسها، يكون الارتفاع 0.

منحدر أي خط عمودي غير محدد. عندما تكون إحداثيات x للخط متشابهة، يكون التشغيل هو 0.

ميل الخط الأفقي والعمودي

ميل الخط الأفقي،$y=b$، يساوي 0.

منحدر الخط العمودي،$x=a$، غير محدد.

مثال$\PageIndex{4}$

ابحث عن ميل كل سطر: ⓐ$x=8$ ⓑ $y=−5$.

إجابة

ⓐ$x=8$
هذا خط عمودي. المنحدر الخاص به غير محدد.
ⓑ$y=−5$
هذا خط أفقي. لديها منحدر 0.

مثال$\PageIndex{5}$

ابحث عن منحدر الخط:$x=−4$.

إجابة

غير محدد

مثال$\PageIndex{6}$

ابحث عن منحدر الخط:$y=7$.

إجابة

0

دليل سريع لمنحدرات الخطوط

سنحتاج أحيانًا إلى إيجاد ميل الخط الفاصل بين نقطتين عندما لا يكون لدينا رسم بياني لحساب الارتفاع والجري. يمكننا رسم النقاط على ورق شبكي، ثم حساب الارتفاع والجري، ولكن كما سنرى، هناك طريقة للعثور على المنحدر بدون رسم بياني. قبل أن نصل إليها، نحتاج إلى إدخال بعض الرموز الجبرية.

لقد رأينا أن الزوج المرتب (x، y) (x، y) يعطي إحداثيات النقطة. ولكن عندما نعمل مع المنحدرات، نستخدم نقطتين. كيف يمكن استخدام نفس الرمز (x، y) (x، y) لتمثيل نقطتين مختلفتين؟ يستخدم علماء الرياضيات مخطوطات لتمييز النقاط.

$\begin{array} {ll} {(x_1, y_1)} &{\text{read “} x \text{ sub } 1, \space y \text{ sub } 1 \text{”}} \\ {(x_2, y_2)} &{\text{read “} x \text{ sub } 2, \space y \text{ sub } 2 \text{”}} \\ \end{array} \nonumber$

سوف نستخدمها$(x_1,y_1)$ لتحديد النقطة الأولى وتحديد النقطة الثانية.$(x_2,y_2)$

إذا كان لدينا أكثر من نقطتين، فيمكننا استخدامها$(x_3,y_3)$$(x_4,y_4)$، وما إلى ذلك.

دعونا نرى كيف يرتبط الارتفاع والجري بإحداثيات النقطتين من خلال إلقاء نظرة أخرى على ميل الخط الفاصل بين النقطتين$(7,6)$،$(2,3)$ وكما هو موضح في هذا الرسم البياني.

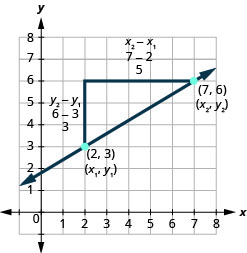
$\begin{array} {ll} {\text{Since we have two points, we will use subscript notation.}} &{ \begin{pmatrix} x_1, & y_1 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ 6 & 6 \end{pmatrix}} \\ {} &{m=\frac{\text{rise}}{\text{run}}} \\ {\text{On the graph, we counted the rise of 3 and the run of 5.}} &{m=\frac{3}{5}} \\ {\text{Notice that the rise of 3 can be found by subtracting the}} &{} \\ {y\text{-coordinates, 6 and 3, and the run of 5 can be found by}} &{} \\ {\text{subtracting the x-coordinates 7 and 2.}} &{} \\ {\text{We rewrite the rise and run by putting in the coordinates.}} &{m=\frac{6-3}{7-2}} \\ {} &{} \\ {\text{But 6 is } y_2 \text{, the y-coordinate of the second point and 3 is }y_1 \text{, the y-coordinate}} &{} \\ {\text{of the first point. So we can rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{7-2}} \\ {\text{Also 7 is the x-coordinate of the second point and 2 is the x-coordinate}} &{} \\ {\text{of the first point. So again we rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ \end{array} \nonumber$

لقد أظهرنا أن$m=\frac{y_2−y_1}{x_2−x_1}$ هذا حقًا إصدار آخر من$m=\frac{\text{rise}}{\text{run}}$. يمكننا استخدام هذه الصيغة لإيجاد ميل الخط المستقيم عندما تكون لدينا نقطتان على الخط.

ميل الخط الفاصل بين نقطتين

ميل الخط الفاصل بين نقطتين$(x_1,y_1)$$(x_2,y_2)$ وهو:

$m=\frac{y_2−y_1}{x_2−x_1}$.

المنحدر هو:

$$y\text{ of the second point minus }y\text{ of the first point} \nonumber$$ $$\text{over} \nonumber$$ $$x\text{ of the second point minus }x\text{ of the first point} \nonumber$$

مثال$\PageIndex{7}$

استخدم صيغة المنحدر للعثور على ميل الخط عبر النقاط$(−2,−3)$ and $(-7,4)$.

إجابة

$\begin{array} {ll} {\text{We’ll call (−2,−3) point #1and (−7,4) point #2.}} &{ \begin{pmatrix} x_1, & y_1 \\ -2 & -3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ -7 & 4 \end{pmatrix}} \\ {\text{Use the slope formula.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{} \\ {\text{x of the second point minus x of the first point}} &{m=\frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify}}&{m=\frac{7}{-5}} \\ {} &{m=\frac{-7}{5}} \\ \end{array} \nonumber$

دعونا نتحقق من هذا المنحدر على الرسم البياني الموضح.

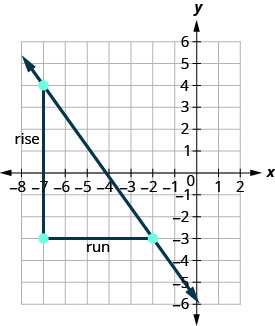
$$m=\frac{\text{rise}}{\text{run}} \nonumber$$ $$m=\frac{7}{−5} \nonumber$$ $$m=\frac{−7}{5} \nonumber$$

استخدم صيغة المنحدر للعثور على ميل الخط عبر زوج النقاط:$(−3,4)$ و$(2,−1)$.

إجابة

$-1$

مثال$\PageIndex{9}$

استخدم صيغة المنحدر للعثور على ميل الخط عبر زوج النقاط:$(−2,6)$ و$(−3,−4)$.

إجابة

10

رسم بياني للخط المستقيم بمعلومية النقطة والمنحدر

حتى الآن، في هذا الفصل، قمنا برسم الخطوط البيانية من خلال رسم النقاط، واستخدام القطع المقطوعة، والتعرف على الخطوط الأفقية والعمودية.

يمكننا أيضًا رسم خط عندما نعرف نقطة واحدة ومنحدر الخط. سنبدأ برسم النقطة ثم نستخدم تعريف المنحدر لرسم الرسم البياني للخط.

مثال$\PageIndex{10}$: How to graph a Line Given a Point and the Slope

ارسم خطًا بيانيًا للخط الذي يمر عبر النقطة$(1,−1)$ التي يكون المنحدر فيها$m=\frac{3}{4}$.

إجابة

يمكنك التحقق من عملك من خلال إيجاد نقطة ثالثة. نظرًا لوجود المنحدر$m=34$، يمكن أيضًا كتابته كـ$m=\frac{−3}{−4}$ (السالب مقسومًا على السالب إيجابي!). ارجع إلى$(1,−1)$ عد الارتفاع$−3$ والركض،$−4$.

مثال$\PageIndex{11}$

ارسم خطًا بيانيًا للخط الذي يمر عبر النقطة$(2,−2$ مع المنحدر$m=\frac{4}{3}$.

إجابة

مثال$\PageIndex{12}$

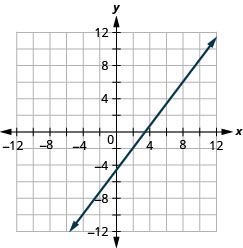
رسم بياني للخط الذي يمر عبر النقطة$(−2,3)$ with the slope $m=\frac{1}{4}$.

إجابة

رسم بياني لخط بمعلومية النقطة والمنحدر.

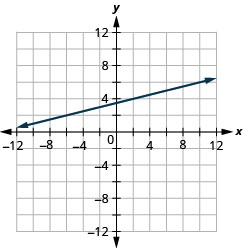
1. ارسم النقطة المعطاة.
2. استخدم صيغة المنحدر$m=\frac{\text{rise}}{\text{run}}$ لتحديد الارتفاع والجري.
3. بدءًا من النقطة المحددة، قم بحساب الارتفاع والجري لتحديد النقطة الثانية.
4. قم بتوصيل النقاط بخط.

رسم خط مستقيم باستخدام ميله والجزء المقطوع منه

لقد قمنا برسم المعادلات الخطية برسم النقاط، واستخدام القطع المقطوعة، والتعرف على الخطوط الأفقية والعمودية، واستخدام نقطة واحدة ومنحدر الخط. بمجرد أن نرى كيفية ارتباط المعادلة في شكل المنحدر - التقاطع والرسم البياني الخاص بها، سيكون لدينا طريقة أخرى يمكننا استخدامها لرسم الخطوط.

انظر الشكل. لنلقِ نظرة على الرسم البياني للمعادلة$y=12x+3$ ونجد ميلها والجزء المقطوع من y.

الشكل$\PageIndex{2}$

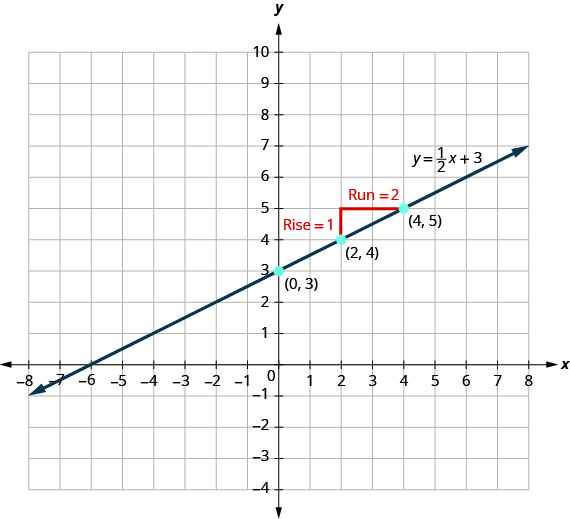
توضح لنا الخطوط الحمراء في الرسم البياني أن الارتفاع هو 1 والركض هو 2. الاستبدال في صيغة المنحدر:

$$m=\frac{\text{rise}}{\text{run}} \nonumber$$ $$m=\frac{1}{2} \nonumber$$

اعتراض y هو$(0,3)$.

انظر إلى معادلة هذا الخط.

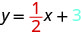
انظر إلى المنحدر ونقطة التقاطع y.

عندما يتم حل معادلة خطية لـ y، يكون معامل الحد x هو المنحدر والحد الثابت هو الإحداثي y للجزء المقطوع y. نقول أن المعادلة$y=12x+3$ في شكل منحدر - مقطع. في بعض الأحيان يُطلق على نموذج المنحدر - التقاطع اسم «y -form».

شكل تقاطع المنحدر لمعادلة الخط المستقيم

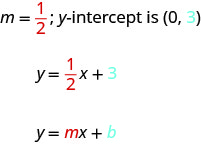
شكل المنحدر والجزء المقطوع لمعادلة الخط المستقيم ذي المنحدر m والجزء المقطوع y$(0,b)$ هو$y=mx+b$.

دعونا نتدرب على إيجاد قيم المنحدر والجزء المقطوع y من معادلة الخط المستقيم.

مثال$\PageIndex{13}$

حدد ميل الخط وقطعه y من المعادلة:

ⓐ$y=−\frac{4}{7}x−2$ ⓑ$x+3y=9$

إجابة

ⓐ نحن نقارن معادلتنا بصيغة المنحدر والمقطع للمعادلة.

اكتب شكل المنحدر والجزء المقطوع لمعادلة الخط المستقيم.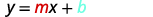
اكتب معادلة الخط المستقيم.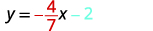
حدد المنحدر.
حدد التقاطع y.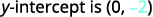

ⓑ عندما لا يتم إعطاء معادلة الخط المستقيم في شكل منحدر، ستكون خطوتنا الأولى هي حل معادلة y.

حل من أجلك.	x+3y=9x+3Y=9
اطرح x من كل جانب.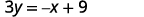
قسّم كلا الجانبين على 3.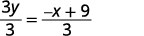
قم بالتبسيط.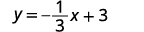
اكتب شكل المنحدر والجزء المقطوع لمعادلة الخط المستقيم.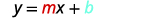
اكتب معادلة الخط المستقيم.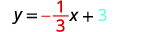
حدد المنحدر.
حدد التقاطع y.

مثال$\PageIndex{14}$

حدد المنحدر والجزء المقطوع y من معادلة الخط المستقيم.

ⓐ$y=\frac{2}{5}x−1$ ⓑ$x+4y=8$

إجابة

ⓐ$m=\frac{2}{5}$؛$(0,−1)$
ⓑ$m=−\frac{1}{4}$؛$(0,2)$

مثال$\PageIndex{15}$

حدد المنحدر والجزء المقطوع y من معادلة الخط المستقيم.

ⓐ$y=−\frac{4}{3} x+1$ ⓑ$3x+2y=12$

إجابة

ⓐ$m=−\frac{4}{3}$؛$(0,1)$
ⓑ$m=−\frac{3}{2}$؛$(0,6)$

لقد رسمنا خطًا بيانيًا باستخدام المنحدر والنقطة. الآن بعد أن عرفنا كيفية إيجاد المنحدر والجزء المقطوع من y لخط من معادلته، يمكننا استخدام التقاطع y كنقطة، ثم عد المنحدر من هناك.

مثال$\PageIndex{16}$

ارسم خط المعادلة$y=−x+4$ using its slope and y Intercept.

إجابة

	$y=mx+b$
توجد المعادلة في صورة منحدر-مقطع.	$y=−x+4$
حدد المنحدر ونقطة التقاطع y.	$m=−1$ اعتراضي الإلكتروني هو$(0,4)$
ارسم نقطة التفتيش الخاصة بي.	انظر الرسم البياني.
حدد الارتفاع أثناء الجري.	$m=−11$
احسب الارتفاع وركض لتحديد النقطة الثانية.	انهض$-1$، اركض$1$

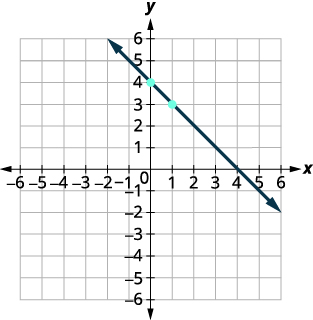
ارسم الخط كما هو موضح في الرسم البياني.

مثال$\PageIndex{17}$

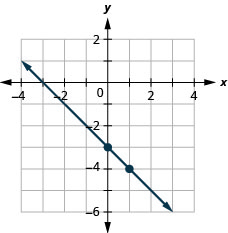
ارسم خط المعادلة بيانيًا$y=−x−3$ باستخدام ميله والجزء المقطوع من y.

إجابة

مثال$\PageIndex{18}$

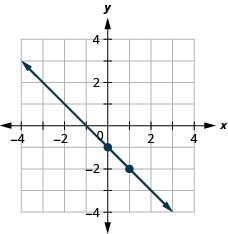
ارسم خط المعادلة بيانيًا$y=−x−1$ باستخدام ميله والجزء المقطوع من y.

إجابة

الآن بعد أن قمنا برسم الخطوط باستخدام المنحدر والجزء المقطوع y، دعونا نلخص جميع الطرق التي استخدمناها لرسم الخطوط.

اختر الطريقة الأكثر ملاءمة لرسم خط

الآن بعد أن رأينا عدة طرق يمكننا استخدامها لرسم الخطوط، كيف نعرف الطريقة التي يجب استخدامها لمعادلة معينة؟

بينما يمكننا رسم النقاط، أو استخدام نموذج التقاطع المنحدر، أو العثور على الأجزاء المقطوعة لأي معادلة، إذا تعرفنا على الطريقة الأكثر ملاءمة لرسم نوع معين من المعادلات، فإن عملنا سيكون أسهل.

بشكل عام، لا يعد رسم النقاط الطريقة الأكثر فعالية لرسم خط. لنبحث عن بعض الأنماط للمساعدة في تحديد الطريقة الأكثر ملاءمة لرسم خط.

فيما يلي خمس معادلات رسمناها بيانيًا في هذا الفصل، والطريقة التي استخدمناها لرسم كل منها بيانيًا.

$$\begin{array} {lll} {} &{\textbf{Equation}} &{\textbf{Method}} \\ {\text{#1}} &{x=2} &{\text{Vertical line}} \\ {\text{#2}} &{y=−1} &{\text{Horizontal line}} \\ {\text{#3}} &{−x+2y=6} &{\text{Intercepts}} \\ {\text{#4}} &{4x−3y=12} &{\text{Intercepts}} \\ {\text{#5}} &{y=−x+4} &{\text{Slope–intercept}} \\ \end{array} \nonumber$$

تحتوي كل من المعادلات #1 و #2 على متغير واحد فقط. تذكر أن قيمة المتغير الواحد ثابتة في معادلات بهذا الشكل؛ ولا تعتمد على قيمة المتغير الآخر. تحتوي معادلات هذا النموذج على رسوم بيانية عبارة عن خطوط رأسية أو أفقية.

في المعادلتين #3 و #4، يوجد كل من x و y على نفس الجانب من المعادلة. هاتان المعادلتان من الشكل Ax+By=C.Ax+By=C. استبدلنا y=0y=0 لإيجاد x - intercept و x=0x=0 للعثور على التقاطع y، ثم عثرنا على نقطة ثالثة باختيار قيمة أخرى لـ x أو y.

تتم كتابة المعادلة #5 في شكل منحدر-مقطع. بعد تحديد المنحدر والجزء المقطوع من المعادلة، استخدمناهما لرسم الخط.

هذا يؤدي إلى الاستراتيجية التالية.

إستراتيجية لاختيار الطريقة الأكثر ملاءمة لرسم خط

ضع في اعتبارك شكل المعادلة.

• إذا كان يحتوي على متغير واحد فقط، فهو خط عمودي أو أفقي.
  • $x=a$هو خط عمودي يمر عبر المحور x عند a.
  • $y=b$هو خط أفقي يمر عبر المحور y عند b.
• إذا تم عزل y على أحد طرفي المعادلة، في النموذج$y=mx+b$، قم بالرسم البياني باستخدام المنحدر والجزء المقطوع y.
  • حدد المنحدر ونقطة التقاطع y ثم قم بالرسم البياني.
• إذا كانت المعادلة من النموذج$Ax+By=C$، فأوجد القطع المقطوعة.
  • ابحث عن نقاط التقاطع x - و y - والنقطة الثالثة، ثم الرسم البياني.

مثال$\PageIndex{19}$

حدد الطريقة الأكثر ملاءمة لرسم كل سطر:

ⓐ$y=5$ ⓑ$4x−5y=20$ ⓒ$x=−3$ ⓓ$y=−\frac{5}{9}x+8$

إجابة

ⓐ تحتوي$y=5$
هذه المعادلة على متغير واحد فقط، y. الرسم البياني الخاص به هو خط أفقي يعبر المحور y عند$5$.
ⓑ$4x−5y=20$
هذه المعادلة هي من النموذج$Ax+By=C$. أسهل طريقة للرسم البياني هي العثور على نقاط الاعتراض ونقطة أخرى.
ⓒ$x=−3$
هناك متغير واحد فقط، x. الرسم البياني عبارة عن خط عمودي يعبر المحور x عند$−3$.
ⓓ$y=−\frac{5}{9}x+8$
نظرًا لأن هذه المعادلة في$y=mx+b$ الشكل، سيكون من الأسهل رسم هذا الخط بيانيًا باستخدام المنحدر وقطرات التقاطع y.

مثال$\PageIndex{20}$

حدد الطريقة الأكثر ملاءمة لرسم كل سطر:

ⓐ$3x+2y=12$ ⓑ$y=4$ ⓒ$y=\frac{1}{5}x−4$ ⓓ$x=−7$.

إجابة

ⓐ عمليات الاعتراض ⓑ الخط الأفقي ⓒ اعتراض المنحدر ⓓ الخط العمودي

مثال$\PageIndex{21}$

حدد الطريقة الأكثر ملاءمة لرسم كل سطر:

ⓐ$x=6$ ⓑ$y=−\frac{3}{4}x+1$ ⓒ$y=−8$ ⓓ$4x−3y=−1$.

إجابة

ⓐ خط عمودي ⓑ اعتراض المنحدر ⓒ خط أفقي
ⓓ عمليات الاعتراض

رسم بياني وتفسير تطبيقات التقاطع المنحدر

تم تصميم العديد من تطبيقات العالم الحقيقي من خلال المعادلات الخطية. سنلقي نظرة على بعض التطبيقات هنا حتى تتمكن من رؤية كيفية ارتباط المعادلات المكتوبة بصيغة التقاطع المنحدر بمواقف العالم الحقيقي.

عادةً، عندما تستخدم نماذج المعادلة الخطية بيانات العالم الحقيقي، يتم استخدام أحرف مختلفة للمتغيرات، بدلاً من استخدام x و y فقط. تذكرنا أسماء المتغيرات بالكميات التي يتم قياسها.

أيضًا، سنحتاج غالبًا إلى توسيع المحاور في نظام الإحداثيات المستطيل الخاص بنا إلى أرقام موجبة وسالبة أكبر لاستيعاب البيانات في التطبيق.

مثال$\PageIndex{22}$

$F=\frac{9}{5}C+32$تُستخدم المعادلة لتحويل درجات الحرارة، C، على مقياس السيلزيوس إلى درجات حرارة، F، على مقياس فهرنهايت.

ⓐ ابحث عن درجة حرارة فهرنهايت لدرجة حرارة مئوية قدرها 0.

ⓑ ابحث عن درجة حرارة فهرنهايت لدرجة حرارة مئوية تبلغ 20 درجة مئوية.

ⓒ قم بتفسير المنحدر والجزء المقطوع من F للمعادلة.

ⓓ رسم المعادلة بيانيًا.

إجابة

ⓐ

$\begin{array} {ll} {\text{Find the Fahrenheit temperature for a Celsius temperature of 0.}} &{F=\frac{9}{5}C+32} \\ {\text{Find F when C=0.}} &{F=\frac{9}{5}(0)+32} \\ {\text{Simplify.}} &{F=32} \\ \end{array} \nonumber$

ⓑ

$\begin{array} {ll} {\text{Find the Fahrenheit temperature for a Celsius temperature of 20.}} &{F=\frac{9}{5}C+32} \\ {\text{Find F when C=20.}} &{F=\frac{9}{5}(20)+32} \\ {\text{Simplify.}} &{F=36+32} \\ {\text{Simplify.}} &{F=68} \\ \end{array} \nonumber$

ⓒ
قم بتفسير المنحدر والجزء المقطوع من F للمعادلة.
على الرغم من أن هذه المعادلة تستخدم F و C، إلا أنها لا تزال في شكل تقاطع منحدر.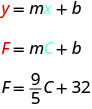

المنحدر$\frac{9}{5}$، يعني أن درجة الحرارة فهرنهايت (F) تزيد 9 درجات عندما تزيد درجة الحرارة المئوية (C) 5 درجات.
يعني التقاطع F أنه عندما تكون درجة الحرارة$0°$ على مقياس سيليسيوس، فإنها تكون$32°$ على مقياس فهرنهايت.
ⓓ رسم المعادلة بيانيًا.
سنحتاج إلى استخدام مقياس أكبر من المعتاد. ابدأ عند التقاطع F$(0,32)$، ثم احسب ارتفاع 9 وجري 5 للحصول على نقطة ثانية كما هو موضح في الرسم البياني.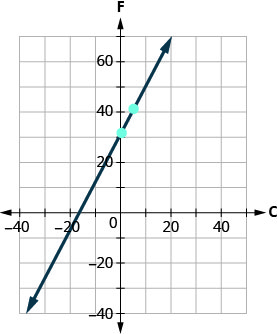

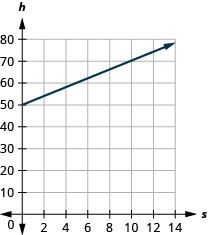
مثال$\PageIndex{23}$

المعادلة\(h=2s+50\) is used to estimate a woman’s height in inches, h، بناءً على حجم حذائها، s.

ⓐ تقدير ارتفاع الطفل الذي يرتدي حذاء نسائي مقاس 0.

ⓑ تقدير ارتفاع المرأة بحجم الحذاء 8.

ⓒ قم بتفسير المنحدر والجزء المقطوع من المعادلة.

ⓓ رسم المعادلة بيانيًا.

إجابة

ⓐ 50 بوصة
ⓑ 66 بوصة
ⓒ المنحدر، 2، يعني أن الارتفاع، ح، يزيد بمقدار 2 بوصة عندما يزداد مقاس الحذاء بمقدار 1. يعني التقاطع h أنه عندما يكون مقاس الحذاء 0، يكون الارتفاع 50 بوصة.
ⓓ

مثال$\PageIndex{24}$

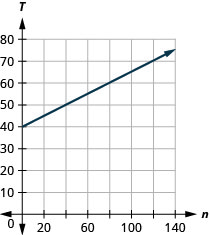
المعادلة\(T=\frac{1}{4}n+40\) is used to estimate the temperature in degrees Fahrenheit, T، بناءً على عدد غردات لعبة الكريكيت، n، في دقيقة واحدة.

ⓐ قم بتقدير درجة الحرارة عند عدم وجود غردات.

ⓑ قم بتقدير درجة الحرارة عندما يكون عدد التغريدات في دقيقة واحدة هو 100.

ⓒ قم بتفسير المنحدر والجزء المتقاطع T للمعادلة.

ⓓ رسم المعادلة بيانيًا.

إجابة

ⓐ 40 درجة
ⓑ 65 درجة
ⓒ المنحدر$\frac{1}{4}$، يعني أن درجة الحرارة فهرنهايت (F) تزداد بمقدار 1 درجة عندما يزداد عدد النرد، n، بمقدار 4. يعني التقاطع T أنه عندما يكون عدد التغريدات 0، تكون درجة الحرارة 40 درجة.
ⓓ

تتكون تكلفة إدارة بعض أنواع الأعمال من عنصرين - تكلفة ثابتة وتكلفة متغيرة. التكلفة الثابتة هي نفسها دائمًا بغض النظر عن عدد الوحدات المنتجة. هذه هي تكلفة الإيجار والتأمين والمعدات والإعلانات وغيرها من العناصر التي يجب دفعها بانتظام. تعتمد التكلفة المتغيرة على عدد الوحدات المنتجة. إنه مخصص للمواد والعمالة اللازمة لإنتاج كل عنصر.

مثال$\PageIndex{25}$

سام يقود شاحنة توصيل. $C=0.5m+60$تُمثِّل المعادلة العلاقة بين تكلفته الأسبوعية، C، بالدولار وعدد الأميال، m، التي يقودها.

ⓐ ابحث عن تكلفة سام لمدة أسبوع عندما يقود 0 أميال.

ⓑ ابحث عن التكلفة لمدة أسبوع عندما يقود 250 ميلاً.

ⓒ قم بتفسير المنحدر والجزء C من المعادلة.

ⓓ رسم المعادلة بيانيًا.

إجابة

ⓐ
$\begin{array} {ll} {\text{Find Sam’s cost for a week when he drives 0 miles.}} &{C=0.5m+60} \\ {\text{Find C when m=0.}} &{C=0.5(0)+60} \\ {\text{Simplify.}} &{C=60} \\ {} &{\text{Sam’s costs are }$\text{60 when he drives 0 miles.}} \\ \end{array} \nonumber$
ⓑ
$\begin{array} {ll} {\text{Find Sam’s cost for a week when he drives 250 miles.}} &{C=0.5m+60} \\ {\text{Find C when m=250.}} &{C=0.5(250)+60} \\ {\text{Simplify.}} &{C=185} \\ {} &{\text{Sam’s costs are }$\text{185 when he drives 250 miles.}} \\ \end{array} \nonumber$
ⓒ قم بتفسير المنحدر والجزء C من المعادلة.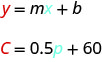

يعني المنحدر، 0.5، أن التكلفة الأسبوعية، C، تزداد بمقدار 0.50 دولارًا عندما يزداد عدد الأميال المقطوعة، n، بمقدار 1.
يعني C -Intercept أنه عندما يكون عدد الأميال المقطوعة هو 0، فإن التكلفة الأسبوعية هي 60 دولارًا.
ⓓ رسم المعادلة بيانيًا.
سنحتاج إلى استخدام مقياس أكبر من المعتاد. ابدأ عند التقاطع C$(0,60)$.

لحساب المنحدر$m= 0.5$، نعيد كتابته ككسر مكافئ يجعل الرسم البياني أسهل.

$\begin{array} {ll} {} &{m=0.5} \\ {\text{Rewrite as a fraction.}} &{m=\frac{0.5}{1}} \\ {\text{Multiply numerator and}} &{} \\ {\text{denominator by 100}} &{m=\frac{0.5(100)}{1(100)}} \\ {\text{Simplify.}} &{m=\frac{50}{100}} \\ \end{array} \nonumber$

لذلك، لرسم بياني، ترتفع النقطة التالية بمقدار 50 من نقطة التقاطع 60 ثم إلى النقطة 100 اليمنى. ستكون النقطة الثانية$(100, 110)$.

مثال$\PageIndex{26}$

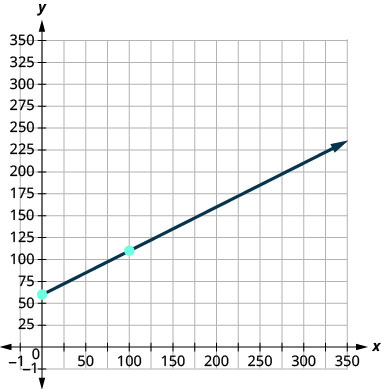
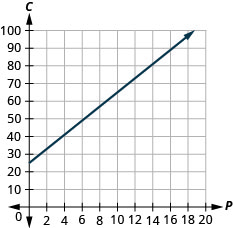
لدى Stella شركة منزلية تبيع البيتزا الذواقة. $C=4p+25$تُمثِّل المعادلة العلاقة بين تكلفتها الأسبوعية، C، بالدولار وعدد البيتزا، p، التي تبيعها.

ⓐ ابحث عن تكلفة ستيلا لمدة أسبوع عندما لا تبيع البيتزا.

ⓑ ابحث عن التكلفة لمدة أسبوع عندما تبيع 15 بيتزا.

ⓒ قم بتفسير المنحدر والجزء C من المعادلة.

ⓓ رسم المعادلة بيانيًا.

إجابة

ⓐ 25 دولارًا
ⓑ 85 دولارًا
ⓒ يعني المنحدر، 4، أن التكلفة الأسبوعية، C، تزداد بمقدار 4 دولارات عندما يزداد عدد البيتزا المباعة، ص، بمقدار 1. يعني C -Intercept أنه عندما يكون عدد البيتزا المباعة 0، فإن التكلفة الأسبوعية هي 25 دولارًا.
ⓓ

مثال$\PageIndex{27}$

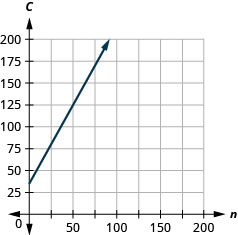
تعمل لورين في مجال الخط. $C=1.8n+35$تُمثل المعادلة العلاقة بين تكلفتها الأسبوعية، C، بالدولار وعدد دعوات الزفاف، n، التي تكتبها.

ⓐ ابحث عن تكلفة لورين لمدة أسبوع عندما لا تكتب أي دعوات.

ⓑ ابحث عن التكلفة لمدة أسبوع عندما تكتب 75 دعوة.

ⓒ قم بتفسير المنحدر والجزء C من المعادلة.

ⓓ رسم المعادلة بيانيًا.

إجابة

ⓐ 35 دولارًا
ⓑ 170 دولارًا
ⓒ المنحدر$1.8$، يعني أن التكلفة الأسبوعية، C، تزداد$$1.80$ عندما يزداد عدد الدعوات، n، بمقدار 1.
تعني C -incept أنه عندما يكون عدد الدعوات 0، تكون التكلفة الأسبوعية 35 دولارًا.
ⓓ

استخدم المنحدرات لتحديد الخطوط المستقيمة المتوازية والمتعامدة

يُطلق على الخطين اللذين لهما نفس المنحدر الخطوط المتوازية. الخطوط المتوازية لها نفس الانحدار ولا تتقاطع أبدًا.

نقول هذا بشكل رسمي أكثر من حيث نظام الإحداثيات المستطيلة. يُطلق على الخطين اللذين لهما نفس المنحدر وخطوط التقاطع المختلفة y -الخطوط المتوازية. انظر الشكل.

الشكل$\PageIndex{3}$

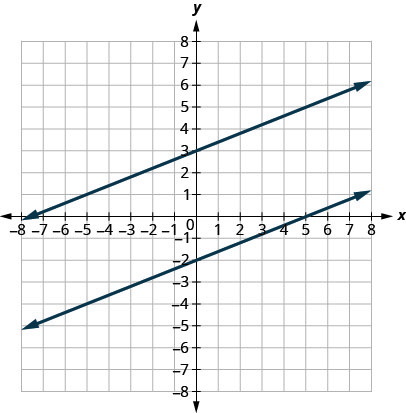
تحقق من أن كلا الخطين لهما نفس المنحدر$m=\frac{2}{5}$، وأن نقاط التقاطع y مختلفة.

ماذا عن الخطوط العمودية؟ ميل الخط العمودي غير محدد، لذلك لا تتناسب الخطوط الرأسية مع التعريف أعلاه. نقول أن الخطوط الرأسية التي تحتوي على تقاطعات x مختلفة متوازية، مثل الخطوط الموضحة في هذا الرسم البياني.

الشكل$\PageIndex{4}$

خطوط متوازية

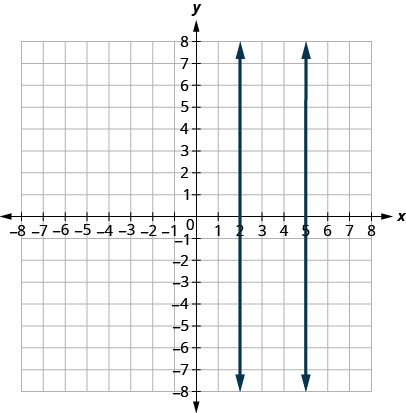
الخطوط المتوازية هي خطوط في نفس المستوى لا تتقاطع.

• تحتوي الخطوط المتوازية على نفس المنحدر ومختلف التقاطعات y.
• إذا كانت m1m1 و m2m2 هي منحدرات خطين متوازيين، فإن m1=m2.m1 = m2.
• تحتوي الخطوط العمودية المتوازية على تقاطعات x مختلفة

نظرًا لأن الخطوط المتوازية لها نفس المنحدر وأجزاء التقاطع y المختلفة، يمكننا الآن النظر فقط إلى شكل المنحدر - التقاطع لمعادلات الخطوط وتحديد ما إذا كانت الخطوط متوازية.

مثال$\PageIndex{28}$

استخدم المنحدرات ونقاط التقاطع y لتحديد ما إذا كانت الخطوط متوازية:

ⓐ$3x−2y=6$ و$y=\frac{3}{2}x+1$ ⓑ$y=2x−3$ و$−6x+3y=−9$.

إجابة

ⓐ تحتوي الخطوط
$\begin{array} {llll} {} &{3x−2y=6} &{\text{and}} &{y=\frac{3}{2}x+1} \\ {} &{−2y=−3x+6} &{} &{} \\ {\text{Solve the first equation for y.}} &{\frac{-2y}{-2}=\frac{-3x+6}{-2}} &{} &{} \\ {\text{The equation is now in slope–intercept form.}} &{y=\frac{3}{2}x−3} &{} &{} \\ {\text{The equation of the second line is already}} &{} &{} &{} \\ {\text{in slope–intercept form.}} &{} &{} &{y=\frac{3}{2}x+1} \\ {} &{} &{} &{} \\ {} &{y=\frac{3}{2}x−3} &{} &{y=\frac{3}{2}x+1} \\ {Identify the slope andy-intercept of both lines.} &{y=mx+b} &{} &{y=mx+b} \\ {} &{m=\frac{3}{2}} &{} &{y=\frac{3}{2}} \\ {} &{\text{y-intercept is }(0,−3)} &{} &{\text{y-intercept is }(0,1)} \\ \end{array} \nonumber$
على نفس المنحدر ومختلف التقاطعات y وبالتالي فهي متوازية.
قد ترغب في رسم الخطوط البيانية لتأكيد ما إذا كانت متوازية.

ⓑ تحتوي الخطوط
$\begin{array} {llll} {} &{y=2x−3} &{\text{and}} &{−6x+3y=−9} \\ {\text{The first equation is already in slope–intercept form.}} &{y=2x−3} &{} &{} \\ {} &{} &{} &{−6x+3y=−9} \\ {} &{} &{} &{3y=6x−9} \\ {\text{Solve the second equation for y.}} &{} &{} &{\frac{3y}{3}=\frac{6x−9}{3}} \\ {} &{} &{} &{y=2x−3} \\ {\text{The second equation is now in slope–intercept form.}} &{} &{} &{y=2x−3} \\ {} &{} &{} &{} \\ {} &{y=2x−3} &{} &{y=2x−3} \\ {\text{Identify the slope andy-intercept of both lines.}} &{y=mx+b} &{} &{y=mx+b} \\ {} &{m=2} &{} &{m=2} \\ {} &{\text{y-intercept is }(0,−3)} &{} &{\text{y-intercept is }(0,-3)} \\ \end{array} \nonumber$
على نفس المنحدر، ولكن لها أيضًا نفس نقاط التقاطع y. تمثل معادلاتهما نفس الخط ونقول أن الخطوط متزامنة. إنها ليست متوازية؛ إنها نفس الخط.

مثال$\PageIndex{29}$

استخدم المنحدرات ونقاط التقاطع y لتحديد ما إذا كانت الخطوط متوازية:

ⓐ$2x+5y=5$ و$y=−\frac{2}{5}x−4$ ⓑ$y=−\frac{1}{2}x−1$ و$x+2y=−2$.

إجابة

ⓐ متوازي ⓑ غير متوازي؛ نفس الخط

مثال$\PageIndex{30}$

استخدم المنحدرات ونقاط التقاطع y لتحديد ما إذا كانت الخطوط متوازية:

ⓐ$4x−3y=6$ و$y=\frac{4}{3}x−1$ ⓑ$y=\frac{3}{4}x−3$ و$3x−4y=12$.

إجابة

ⓐ متوازي ⓑ غير متوازي؛ نفس الخط

مثال$\PageIndex{31}$

استخدم المنحدرات ونقاط التقاطع y لتحديد ما إذا كانت الخطوط متوازية:

ⓐ$y=−4$ و$y=3$ ⓑ$x=−2$ و$x=−5$.

إجابة

ⓐ$y=−4$ و$y=3$

ندرك على الفور من المعادلات أن هذه خطوط أفقية، وبالتالي نعرف أن منحدرهما كلاهما 0.
بما أن الخطوط الأفقية تعبر المحور y عند y=−4y=−4 وعند y=3، y=3، فإننا نعرف أن التقاطعات y هي (0، −4) (0، −4) و (0,3). (0,3).
تحتوي الخطوط على نفس المنحدر ومختلف التقاطعات y وبالتالي فهي متوازية.

ⓑ$x=−2$ و$x=−5$

ندرك على الفور من المعادلات أن هذه خطوط عمودية، ولذا فإننا نعرف أن منحدراتها غير محددة.
نظرًا لأن الخطوط الرأسية تعبر المحور x عند$x=−2$ و$x=−5$، فإننا نعلم أن نقاط التقاطع y هي$(−2,0)$ و$(−5,0)$.
الخطوط عمودية ولها تقاطعات x مختلفة وبالتالي فهي متوازية.

مثال$\PageIndex{32}$

استخدم المنحدرات ونقاط التقاطع y لتحديد ما إذا كانت الخطوط متوازية:

ⓐ$y=8$ و$y=−6$ ⓑ$x=1$ و$x=−5$.

إجابة

ⓐ متوازي ⓑ متوازي

مثال$\PageIndex{33}$

استخدم المنحدرات ونقاط التقاطع y لتحديد ما إذا كانت الخطوط متوازية:

ⓐ$y=1$ و$y=−5$ ⓑ$x=8$ و$x=−6$.

إجابة

ⓐ متوازي ⓑ متوازي

دعونا ننظر إلى الخطوط التي معادلاتها هي$y=\frac{1}{4}x−1$ و$y=−4x+2$، كما هو موضح في الشكل.

الشكل$\PageIndex{5}$

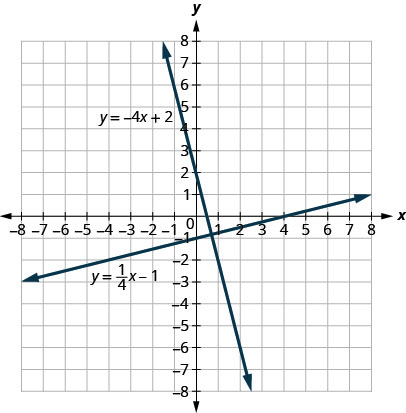
تقع هذه الخطوط في نفس المستوى وتتقاطع في الزوايا الصحيحة. نسمي هذه الخطوط العمودية.

إذا نظرنا إلى ميل الخط الأول$m_1=\frac{1}{4}$، ومنحدر الخط الثاني$m_2=−4$، يمكننا أن نرى أنهما تبادلات سالبة لبعضهما البعض. إذا قمنا بمضاعفتها، فإن منتجها هو$−1$.

$$\begin{array} {l} {m_1·m_2} \\ {14(−4)} \\ {−1} \\ \end{array} \nonumber$$

هذا صحيح دائمًا بالنسبة للخطوط العمودية ويقودنا إلى هذا التعريف.

الخطوط المتعامدة

الخطوط العمودية هي خطوط في نفس المستوى تشكل زاوية قائمة.

• إذا كانت$m_1$ منحدرات خطين عموديين كذلك، فعندئذٍ:$m_2$
  • منحدراتها هي ردود فعل سلبية لبعضها البعض،$m_1=−\frac{1}{m_2}$.
  • نتاج منحدراتها هو$−1$،$m_1·m_2=−1$.
• دائمًا ما يكون الخط العمودي والخط الأفقي متعامدين مع بعضهما البعض

تمكنا من النظر إلى شكل المنحدر - التقاطع للمعادلات الخطية وتحديد ما إذا كانت الخطوط متوازية أم لا. يمكننا أن نفعل نفس الشيء للخطوط العمودية.

نجد صيغة المنحدر-التقاطع للمعادلة، ثم نرى ما إذا كانت المنحدرات عبارة عن تبادلات متقابلة. إذا كان ناتج المنحدرات هو$−1$، تكون الخطوط متعامدة.

مثال$\PageIndex{34}$

استخدم المنحدرات لتحديد ما إذا كانت الخطوط متعامدة:

ⓐ$y=−5x−4$ و$x−5y=5$ ⓑ$7x+2y=3$ و$2x+7y=5$

إجابة

ⓐ
المعادلة الأولى في شكل منحدر-قطع. حل المعادلة الثانية لـ. حدِّد ميل كل خط.Y=−5x−4YM1=−5X−4=MX+B=−5X−5Y−5Y−5Y=5Y=5=5=−x+5=15x−5=15x−1YM2=15x−1YM2=15x−MxB=المعادلة الأولى بصيغة المنحدر-الجزء المقطوع. Y=−5x−4حل المعادلة الثانية لـ.x−5y=5−5y=−x+5−5y−5=−x+5 −5Y=15x−1حدد ميل كل سطر.y=−5x−4y=mx+bm1=−5y=15x−1y=mx+bm2=15
المنحدرات عبارة عن تبادلات سالبة لبعضها البعض، وبالتالي تكون الخطوط متعامدة. نتحقق من ذلك بضرب المنحدرات، حيث إن −5 (15) =−1، −5 (15) =−1، فإنه يتحقق.

ⓑ
حل المعادلات لـ. حدد ميل كل سطر.7X+2Y2Y2Y2Y=3=−7X+3=−7X+32=−72X+32YM=MX+B=−7Y7Y7Y=5=−2x+2x+57Y1=MX+B=−27X+57YM1=MX+B=−27حل المعادلات Y.7x+2Y=32Y=32Y=−7X+32Y2=−7X+32Y=−72X+7Y = 57Y=−2X+57Y7=−2x+57Y=−27X+57Y=−27X+57D منحدر كل خط.y=mx+bm1=−72y=mx+bm1=−27
المنحدرات عبارة عن تبادلات لبعضها البعض، ولكن لها نفس العلامة. نظرًا لأنها ليست تبادلات سالبة، فإن الخطوط ليست متعامدة.

مثال$\PageIndex{3}$

استخدم المنحدرات لتحديد ما إذا كانت الخطوط متعامدة:

ⓐ$y=−3x+2$ و$x−3y=4$ ⓑ$5x+4y=1$ و$4x+5y=3$.

إجابة

ⓐ عمودي ⓑ غير عمودي

مثال$\PageIndex{3}$

استخدم المنحدرات لتحديد ما إذا كانت الخطوط متعامدة:

ⓐ$y=2x−5$ و$x+2y=−6$ ⓑ$2x−9y=3$ و$9x−2y=1$.

إجابة

ⓐ عمودي ⓑ غير عمودي

المفاهيم الرئيسية

• ميل الخط
  • منحدر الخط هو$m=\frac{\text{rise}}{\text{run}}$.
  • يقيس الارتفاع التغيير الرأسي ويقيس الجري التغيير الأفقي.
    
    
    
• كيفية إيجاد ميل الخط من الرسم البياني الخاص به باستخدام$m=\frac{\text{rise}}{\text{run}}$.
  1. حدد موقع نقطتين على الخط الذي تكون إحداثياته عبارة عن أعداد صحيحة.
  2. بدءًا من نقطة واحدة، ارسم مثلثًا قائمًا، بدءًا من النقطة الأولى إلى النقطة الثانية.
  3. احسب الارتفاع والجري على أرجل المثلث.
  4. خذ نسبة الارتفاع للركض للعثور على المنحدر:$m=\frac{\text{rise}}{\text{run}}$.

• ميل الخط الفاصل بين نقطتين.
  • ميل الخط الفاصل بين نقطتين$(x_1,y_1)$$(x_2,y_2)$ وهو:

    $$m=\frac{y_2−y_1}{x_2−x_1} \nonumber$$ .

• كيفية رسم خط بمعلومية النقطة والمنحدر.
  1. ارسم النقطة المعطاة.
  2. استخدم صيغة المنحدر$m=\frac{\text{rise}}{\text{run}}$ لتحديد الارتفاع والجري.
  3. بدءًا من النقطة المحددة، قم بحساب الارتفاع والجري لتحديد النقطة الثانية.
  4. قم بتوصيل النقاط بخط.
• صورة تقاطع المنحدر لمعادلة الخط المستقيم
  • شكل المنحدر والجزء المقطوع لمعادلة الخط المستقيم ذي المنحدر m والجزء المقطوع y$(0,b)$ هو$y=mx+b$
  • 
• الخطوط المتوازية
  • الخطوط المتوازية هي خطوط في نفس المستوى لا تتقاطع.
    تحتوي الخطوط المتوازية على نفس المنحدر ومختلف التقاطعات y.
    إذا كانت منحدرات خطين متوازيين$m_1$ وما$m_2$ زالت كذلك$m_1=m_2$.
    تحتوي الخطوط العمودية المتوازية على تقاطعات x مختلفة.
• الخطوط المتعامدة
  • الخطوط العمودية هي خطوط في نفس المستوى تشكل زاوية قائمة.
  • إذا كانت$m_1$ منحدرات خطين عموديين كما$m_2$ هي، فإن:
    منحدرهما عبارة عن تبادلات سلبية لبعضهما البعض$m_1=−\frac{1}{m_2}$.
    نتاج منحدراتها هو$−1$،$m_1·m_2=−1$.
  • دائمًا ما يكون الخط العمودي والخط الأفقي متعامدين مع بعضهما البعض.

مسرد المصطلحات

خطوط متوازية

الخطوط المتوازية هي خطوط في نفس المستوى لا تتقاطع.

خطوط عمودية

الخطوط العمودية هي خطوط في نفس المستوى تشكل زاوية قائمة.