3.2: رسم بياني للمعادلات الخطية في متغيرين
- Page ID
- 201410
في نهاية هذا القسم، ستكون قادرًا على:
- نقاط الرسم في نظام الإحداثيات المستطيل
- رسم معادلة خطية برسم النقاط
- رسم بياني للخطوط الرأسية والأفقية
- ابحث عن\(x\) - و\(y\) - المعترضين
- رسم خط بياني باستخدام عمليات الاعتراض
رسم النقاط على نظام الإحداثيات المستطيلة
تمامًا مثل الخرائط التي تستخدم نظام الشبكة لتحديد المواقع، يتم استخدام نظام الشبكة في الجبر لإظهار العلاقة بين متغيرين في نظام الإحداثيات المستطيل. يُطلق على نظام الإحداثيات المستطيلة أيضًا اسم\(xy\) -plane أو «المستوى الإحداثي».
يتكون نظام الإحداثيات المستطيلة من خطي أرقام متقاطعين، أحدهما أفقي والآخر عمودي. يُطلق على خط الأعداد الأفقي اسم\(x\) المحور -. يُطلق على خط الأعداد العمودي اسم\(y\) المحور -. تقسم هذه المحاور المستوى إلى أربع مناطق تسمى الأرباع. يتم تحديد الأرباع بالأرقام الرومانية، التي تبدأ من أعلى اليمين وتستمر بعكس اتجاه عقارب الساعة. انظر الشكل\(\PageIndex{1}\).
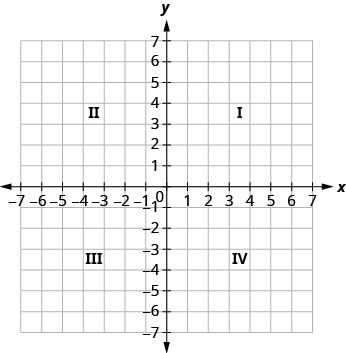
في نظام الإحداثيات المستطيلة، يتم تمثيل كل نقطة بزوج مرتب. الرقم الأول في الزوج المُرتب هو\(x\) الإحداثي -للنقطة، والرقم الثاني هو\(y\) الإحداثي -للنقطة. تعني عبارة «الزوج المطلوب» أن الطلب مهم.
زوج مرتب،\((x,y)\) يعطي إحداثيات نقطة في نظام إحداثيات مستطيل. الرقم الأول هو\(x\) الإحداثيات -. الرقم الثاني هو\(y\) الإحداثيات -.
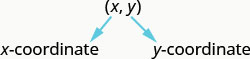
ما الزوج المُرتب للنقطة التي تتقاطع فيها المحاور؟ عند هذه النقطة يكون كلا الإحداثيين صفرًا، لذا فإن الزوج\((0,0)\) المطلوب هو .النقطة\((0,0)\) لها اسم خاص. يطلق عليه الأصل.
هذه النقطة\((0,0)\) تسمى الأصل. إنها النقطة التي يتقاطع فيها\(x\) المحور\(y\) -المحور والمحور.
نحن نستخدم الإحداثيات لتحديد نقطة على\(xy\) الطائرة. دعونا نرسم النقطة\((1,3)\) كمثال. أولاً، حدد موقع 1 على\(x\) المحور -وارسم خطًا رأسيًا برفق من خلاله\(x=1\). ثم حدد الموقع\(3\) على\(y\) المحور -وارسم خطًا أفقيًا\(y=3.\) حتى الآن، ابحث عن النقطة التي يلتقي فيها هذان الخطان - وهي النقطة ذات الإحداثيات\((1,3)\). انظر الشكل\(\PageIndex{2}\).
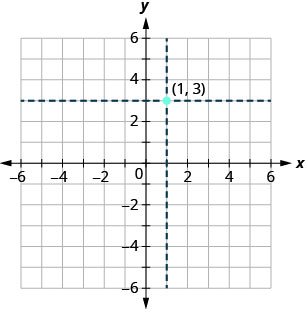
لاحظ أن الخط العمودي الذي يمر\(x=1\) والخط الأفقي من خلاله\(y=3\) ليسا جزءًا من الرسم البياني. لقد استخدمناها فقط لمساعدتنا في تحديد النقطة\((1,3)\).
عندما يكون أحد الإحداثيات صفرًا، تقع النقطة على أحد المحاور. في\(\PageIndex{3},\) الشكل،\((0,4)\) تكون النقطة على\(y\) المحور -والنقطة\((−2,0)\) على\(x\) المحور -.
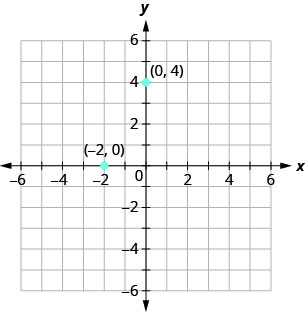
- النقاط ذات\(y\) الإحداثيات -تساوي\(0\) موجودة على\(x\) المحور -ولها إحداثيات\((a,0)\).
- النقاط ذات\(x\) الإحداثي -يساوي\(0\) وجودها على\(y\) المحور -ولها إحداثيات\((0,b)\).
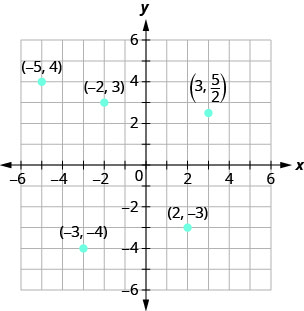
ارسم كل نقطة في نظام الإحداثيات المستطيلة وحدد الربع الذي توجد فيه النقطة:
أ.\((−5,4\)) ب.\((−3,−4)\) ج.\((2,−3)\) د.\((0,−1)\) ه\((3,\dfrac{5}{2})\).
الحل
الرقم الأول من زوج الإحداثيات هو\(x\) -conditate، والرقم الثاني هو\(y\) -conditate. لرسم كل نقطة، ارسم خطًا رأسيًا من خلال\(x\) الإحداثيات -وخط أفقي من خلال\(y\) الإحداثيات -. تقاطعهم هو النقطة.
- نظرًا لأن\(x=−5\) النقطة تقع على يسار\(y\) المحور -. أيضًا\(y=4\)، نظرًا لأن النقطة أعلى من\(x\) المحور -. النقطة\((−5,4)\) في الربع الثاني.
- نظرًا لأن\(x=−3\) النقطة تقع على يسار\(y\) المحور -. أيضًا\(y=−4\)، نظرًا لأن النقطة تقع أسفل\(x\) المحور -. النقطة\((−3,−4)\) في الربع الثالث.
- نظرًا لأن\(x=2\) النقطة تقع على يمين\(y\) المحور -. نظرًا لأن\(y=−3\) النقطة تقع أسفل\(x\) المحور -. النقطة\((2,−3)\) في الربع الرابع.
- نظرًا لأن\(x=0\) النقطة التي تكون إحداثياتها\((0,−1)\) موجودة على\(y\) المحور -.
- نظرًا لأن\(x=3\) النقطة تقع على يمين\(y\) المحور -. نظرًا لأن\(y=\dfrac{5}{2})\) النقطة أعلى من\(x\) المحور -. (قد يكون من المفيد الكتابة\(\dfrac{5}{2})\) كرقم مختلط أو عشري.) النقطة\((3,\dfrac{5}{2})\) في الربع الأول.
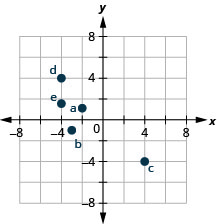
ارسم كل نقطة في نظام إحداثيات مستطيل وحدد الربع الذي توجد فيه النقطة:
أ.\((−2,1)\) ب.\((−3,−1)\) ج.\((4,−4)\) د.\((−4,4)\) ه.\((−4,\dfrac{3}{2})\)
- إجابة
-
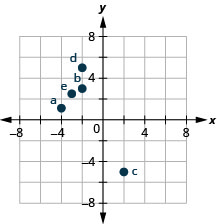
ارسم كل نقطة في نظام إحداثيات مستطيل وحدد الربع الذي توجد فيه النقطة:
أ.\((−4,1)\) ب.\((−2,3)\) ج.\((2,−5)\) د.\((−2,5)\) ه.\((−3,\dfrac{5}{2})\)
- إجابة
-
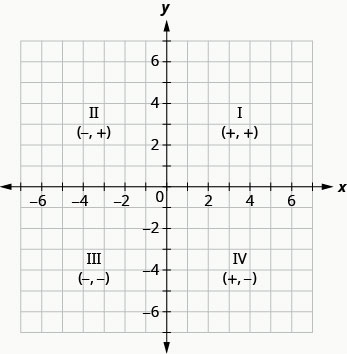
تؤثر علامات\(x\) -conditate و\(y\) -conditate على موقع النقاط. ربما لاحظت بعض الأنماط أثناء رسم النقاط في المثال السابق. يمكننا تلخيص أنماط علامات الأرباع بهذه الطريقة:
| الربع الأول | الربع الثاني | الربع الثالث | الربع الرابع |
| \((x,y)\) | \((x,y)\) | \((x,y)\) | \((x,y)\) |
| \((+,+)\) | \((−,+)\) | \((−,−)\) | \((+,−)\) |
حتى الآن، كانت جميع المعادلات التي قمت بحلها عبارة عن معادلات ذات متغير واحد فقط. في كل حالة تقريبًا، عندما قمت بحل المعادلة، حصلت على حل واحد بالضبط. ولكن يمكن أن تحتوي المعادلات على أكثر من متغير واحد. قد تكون المعادلات ذات المتغيرين من الشكل\(Ax+By=C\). تُسمى معادلة بهذا الشكل معادلة خطية في متغيرين.
\(B\)تُسمى معادلة النموذج\(Ax+By=C\)، حيث\(A\) لا يكون كلاهما صفرًا، بالمعادلة الخطية في متغيرين.
فيما يلي مثال لمعادلة خطية في متغيرين،\(x\) و\(y\).
\ (\ ابدأ {محاذاة\} {\ اللون {\ اللون {أحمر القرميد} A} x + {\ اللون {\ أزرق ملكي} B} y &= {\ اللون {\ اللون {\ اللون {\\ اللون {\ أخضر الغابة} C}\\\ [5pt]
x+ {\ اللون {أزرق ملكي} 4} y &= {\ لون {\ لون {\ لون {\ لون {\ لون {\ لون {\ لون {\ لون {\ لون {
\({\color{BrickRed}A = 1}\)،\({\color{RoyalBlue}B = 4}\)،\({\color{forestgreen}C=8}\)
المعادلة\(y=−3x+5\) هي أيضًا معادلة خطية. ولكن لا يبدو أنها في الشكل\(Ax+By=C\). يمكننا استخدام خاصية إضافة المساواة وإعادة كتابتها في\(Ax+By=C\) الشكل.
\[ \begin{array} {lrll} {} &{y} &= &{-3x+5} \\ {\text{Add to both sides.} } &{y+3x} &= &{3x+5+3x} \\ {\text{Simplify.} } &{y+3x} &= &{5} \\ {\text{Use the Commutative Property to put it in} } &{} &{} &{} \\ {Ax+By=C\text{ form.} } &{3x+y} &= &{5} \end{array} \nonumber\]
من خلال إعادة الكتابة\(y=−3x+5\) كـ\(3x+y=5\)، يمكننا أن نرى بسهولة أنها معادلة خطية في متغيرين لأنها من الشكل\(Ax+By=C\). عندما تكون المعادلة في الشكل\(Ax+By=C\)، نقول إنها في الشكل القياسي لمعادلة خطية.
تكون المعادلة الخطية في شكل قياسي عند كتابتها\(Ax+By=C\).
يفضل معظم الناس أن\(C\) يكون لديهم\(A,\)\(B,\) أعداد صحيحة وأن يكونوا كذلك\(A \geq 0\) وعند كتابة معادلة خطية في شكل قياسي، على الرغم من أنها ليست ضرورية تمامًا.
تحتوي المعادلات الخطية على العديد من الحلول بلا حدود. لكل رقم يتم استبداله\(x\) هناك\(y\) قيمة -مقابلة. هذا الزوج من القيم هو حل للمعادلة الخطية ويتم تمثيله بالزوج المرتب\((x,y)\). عندما نستبدل هذه القيم\(x\)\(y\) بالمعادلة، تكون النتيجة عبارة حقيقية، لأن القيمة الموجودة على الجانب الأيسر تساوي القيمة الموجودة على الجانب الأيمن.
\((x,y)\)يعتبر الزوج المُرتب حلاً للمعادلة الخطية\(Ax+By=C\)، إذا كانت المعادلة عبارة حقيقية عندما يتم استبدال\(y\) القيمتين\(x\) - و - للزوج المُرتب في المعادلة.
تحتوي المعادلات الخطية على العديد من الحلول بلا حدود. يمكننا رسم هذه الحلول في نظام الإحداثيات المستطيلة. ستصطف النقاط بشكل مثالي في خط مستقيم. نربط النقاط بخط مستقيم للحصول على الرسم البياني للمعادلة. نضع الأسهم على طرفي كل جانب من الخط للإشارة إلى أن الخط يستمر في كلا الاتجاهين.
الرسم البياني هو تمثيل مرئي لجميع حلول المعادلة. إنه مثال على قول «الصورة تساوي ألف كلمة». يعرض لك الخط جميع الحلول لهذه المعادلة. كل نقطة على الخط هي حل المعادلة. وكل حل لهذه المعادلة موجود على هذا الخط. هذا الخط يسمى الرسم البياني للمعادلة. النقاط غير الموجودة على الخط ليست حلولًا!
الرسم البياني للمعادلة الخطية\(Ax+By=C\) هو خط مستقيم.
- كل نقطة على الخط هي حل المعادلة.
- كل حل لهذه المعادلة هو نقطة على هذا الخط.
\(y=2x−3\)يتم عرض الرسم البياني لـ.
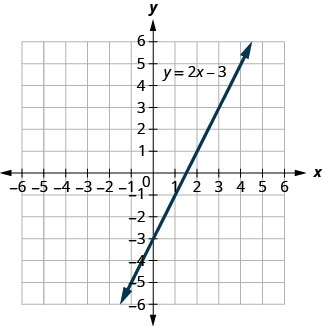
بالنسبة لكل زوج تم طلبه، قرر:
- هل يمثل الزوج المرتب حلاً للمعادلة؟
- هل النقطة على الخط؟
أ:\((0,−3)\) ب:\((3,3)\) ج:\((2,−3)\) د:\((−1,−5)\)
الحل:
استبدل\(x\) القيمتين - و\(y\) -في المعادلة للتحقق مما إذا كان الزوج المرتب حلاً للمعادلة.
أ.
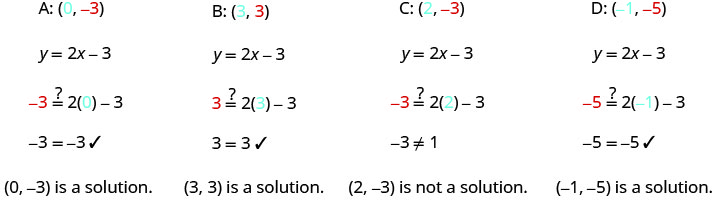
ب. رسم النقاط\((0,−3)\) و\((3,3)\)\((2,−3)\) و و\((−1,−5)\).
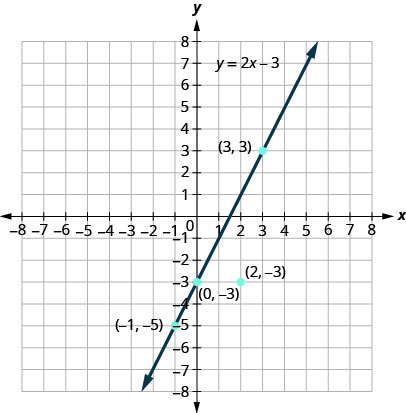
النقاط\((0,3)\)\((3,−3)\)، و،\((−1,−5)\) موجودة على الخط\(y=2x−3\)، والنقطة\((2,−3)\) ليست على الخط.
أما النقاط التي تمثل حلولاً\(y=2x−3\) فهي على المحك، ولكن النقطة التي لا تمثل حلاً ليست على المحك.
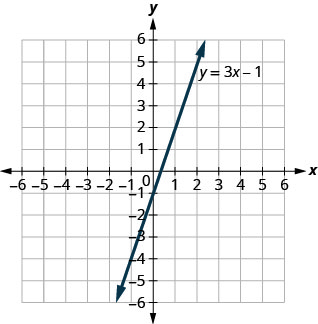
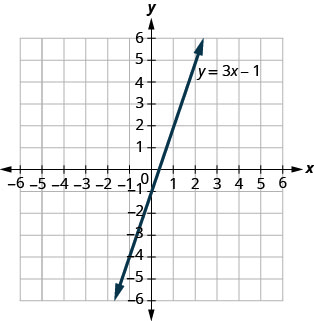
استخدم الرسم البياني لـ\(y=3x−1\). بالنسبة لكل زوج تم طلبه، قرر:
أ. هل يعتبر الزوج المرتب حلاً للمعادلة؟
ب. هل النقطة على الخط؟
أ\((0,−1)\) ب\((2,5)\)
- إجابة
-
أ. نعم ب. نعم
استخدم الرسم البياني لـ\(y=3x−1\). بالنسبة لكل زوج تم طلبه، قرر:
أ. هل يعتبر الزوج المرتب حلاً للمعادلة؟
ب. هل النقطة على الخط؟
أ\((3,−1)\) ب\((−1,−4)\)
- إجابة
-
أ. لا ب. نعم
رسم معادلة خطية بيانيًا عن طريق رسم النقاط
هناك العديد من الطرق التي يمكن استخدامها لرسم معادلة خطية. الطريقة الأولى التي سنستخدمها تسمى نقاط التخطيط، أو طريقة التخطيط بالنقاط. نجد ثلاث نقاط تمثل إحداثياتها حلولًا للمعادلة ثم نرسمها في نظام إحداثيات مستطيل. من خلال ربط هذه النقاط في خط مستقيم، نحصل على الرسم البياني للمعادلة الخطية.
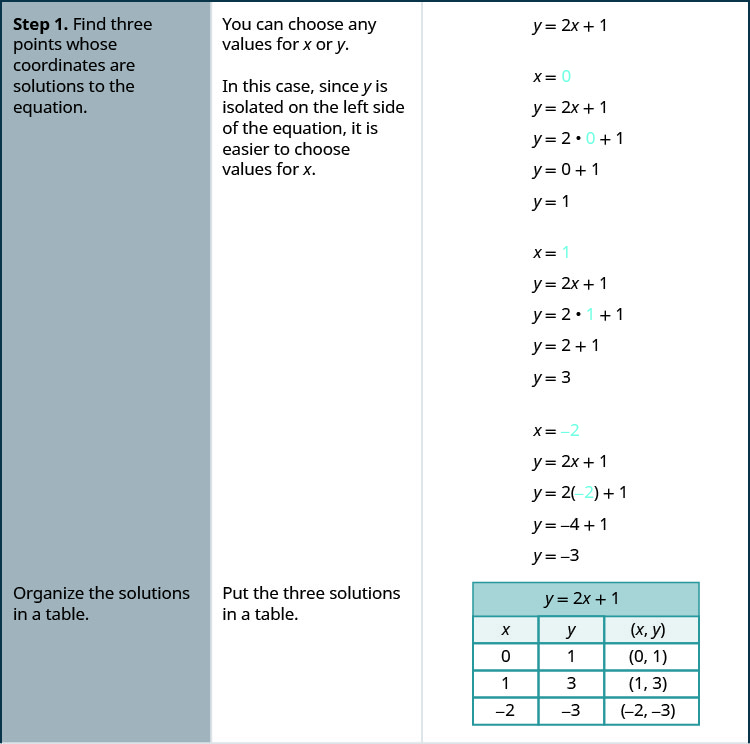
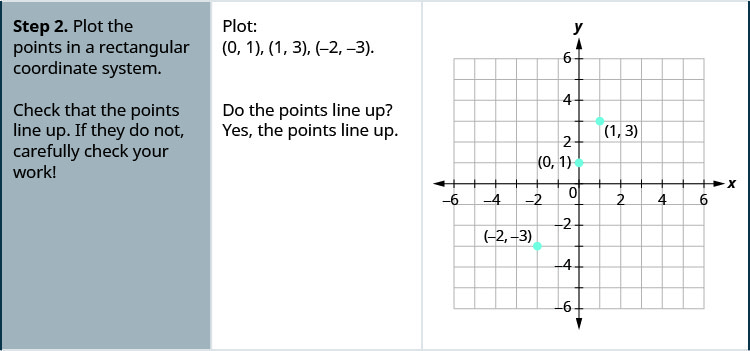
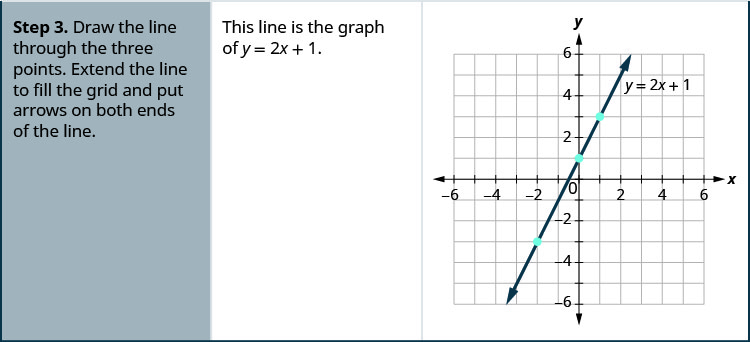
ارسم المعادلة بيانيًا\(y=2x+1\) عن طريق رسم النقاط.
الحل:
قم برسم المعادلة برسم النقاط:\(y=2x−3\).
- إجابة
-
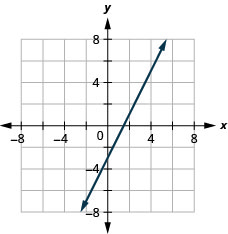
قم برسم المعادلة برسم النقاط:\(y=−2x+4\).
- إجابة
-
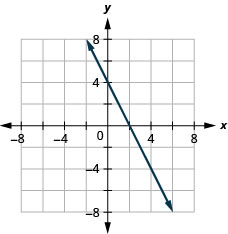
يتم تلخيص الخطوات التي يجب اتخاذها عند رسم معادلة خطية برسم النقاط هنا.
- ابحث عن ثلاث نقاط تمثل إحداثياتها حلولًا للمعادلة. قم بتنظيمها في جدول.
- ارسم النقاط في نظام إحداثيات مستطيل. تحقق من أن النقاط تصطف. إذا لم يفعلوا ذلك، تحقق بعناية من عملك.
- ارسم الخط من خلال النقاط الثلاث. قم بتوسيع الخط لملء الشبكة ووضع الأسهم على طرفي الخط.
صحيح أن تحديد الخط يتطلب نقطتين فقط، ولكن من الجيد استخدام ثلاث نقاط. إذا قمت برسم نقطتين فقط وكانت إحداهما غير صحيحة، فلا يزال بإمكانك رسم خط ولكنه لن يمثل حلول المعادلة. سيكون الخط الخطأ.
إذا استخدمت ثلاث نقاط، وكانت واحدة غير صحيحة، فلن تصطف النقاط. هذا يخبرك بوجود خطأ ما وتحتاج إلى التحقق من عملك. انظر إلى الفرق بين هذه الرسوم التوضيحية.

عندما تتضمن المعادلة كسرًا كمعامل، لا يزال\(x,\) بإمكاننا استبدال أي أرقام بـ\(x.\) لكن الحساب يكون أسهل إذا اتخذنا خيارات «جيدة» لقيم\(x.\) هذه الطريقة سنتجنب الإجابات الكسرية، والتي يصعب رسمها بيانيًا بدقة.
رسم المعادلة بيانيًا:\(y=\frac{1}{2}x+3\).
الحل:
ابحث عن ثلاث نقاط تمثل حلولًا للمعادلة. نظرًا لأن هذه المعادلة تحتوي على الكسر\(\dfrac{1}{2}\) كمعامل،\(x,\) فسنختار القيم\(x\) بعناية. سنستخدم الصفر كخيار واحد ومضاعفات\(2\) الخيارات الأخرى. لماذا تعتبر مضاعفات اثنين اختيارًا جيدًا لقيم\(x\)؟ عن طريق اختيار مضاعفات الضرب\(2\) عن طريق\(\dfrac{1}{2}\) التبسيط إلى رقم صحيح
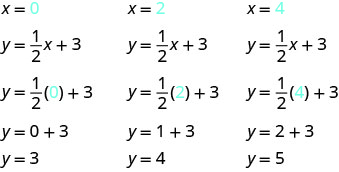
يتم عرض النقاط في الجدول.
| \(y=\frac{1}{2}x+3\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 3 | \((0,3)\) |
| 2 | 4 | \((2,4)\) |
| 4 | 5 | \((4,5)\) |
ارسم النقاط وتحقق من أنها تصطف وارسم الخط.
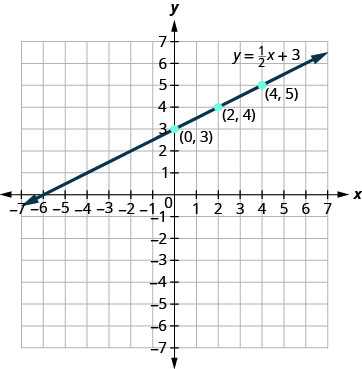
رسم المعادلة بيانيًا:\(y=\frac{1}{3}x−1\).
- إجابة
-
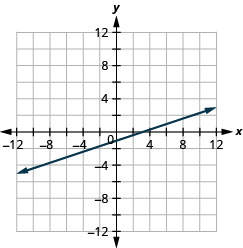
رسم المعادلة بيانيًا:\(y=\frac{1}{4}x+2\).
- إجابة
-
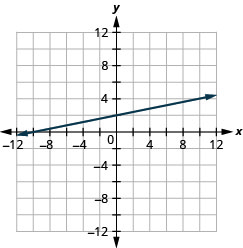
رسم بياني للخطوط الرأسية والأفقية
تحتوي بعض المعادلات الخطية على متغير واحد فقط. قد يكون لديهم فقط\(x\) ولا\(y,\) شيء أو\(y\) بدونه.\(x.\) هذا يغير كيفية عمل جدول القيم للحصول على النقاط لرسمها.
دعونا ننظر في المعادلة\(x=−3\). تحتوي هذه المعادلة\(x.\) على متغير واحد فقط، تقول المعادلة أنه دائمًا\(x\) يساوي\(−3\)، لذلك لا تعتمد قيمته على\(y.\) بغض النظر\(y,\) عن قيمة القيمة\(x\) دائمًا\(−3\).
لذلك لإنشاء جدول للقيم، اكتب\(−3\) جميع\(x\) القيم -values. ثم اختر أي قيم لـ\(y.\)\(x\) Since لا تعتمد على\(y,\) يمكنك اختيار أي أرقام تريدها. ولكن لملاءمة النقاط على الرسم البياني الإحداثي الخاص بنا، سنستخدم 1 و 2 و 3\(y\) للإحداثيات -. انظر الجدول.
| \(x=−3\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| \(−3\) | 1 | \((−3,1)\) |
| \(−3\) | 2 | \((−3,2)\) |
| \((−3,)\) | 3 | \((−3,3)\) |
ارسم النقاط من الجدول وقم بتوصيلها بخط مستقيم. لاحظ أننا رسمنا خطًا رأسيًا.
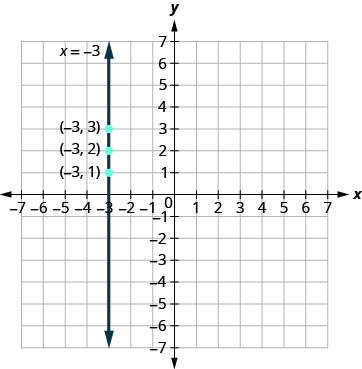
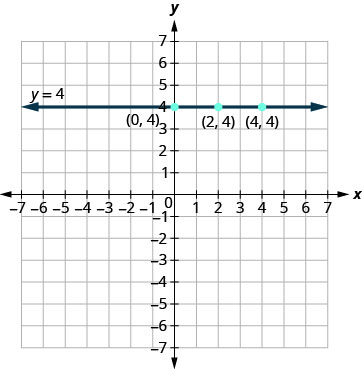
ماذا لو كانت المعادلة تحتوي\(y\) على لا\(x\)؟ دعونا نرسم المعادلة بيانيًا\(y=4\). هذه المرة تكون القيمة y- ثابتة، لذا في هذه المعادلة،\(y\) لا تعتمد على\(x.\)\(4\) Fill in لجميع القيم الموجودة في الجدول ثم اختيار أي قيم لـ\(x.\) سنستخدم 0 و 2 و 4\(x\) للإحداثيات -.\(y\)
| \(y=4\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 4 | \((0,4)\) |
| 2 | 4 | \((2,4)\) |
| 4 | 4 | \((4,4)\) |
في هذا الشكل، قمنا برسم خط أفقي يمر عبر\(y\) المحور السيني عند\(4.\)
الخط العمودي هو الرسم البياني لمعادلة النموذج\(x=a\).
يمر الخط عبر\(x\) المحور -عند\((a,0)\).
الخط الأفقي هو الرسم البياني لمعادلة النموذج\(y=b\).
يمر الخط عبر\(y\) المحور -عند\((0,b)\).
الرسم البياني: أ.\(x=2\) ب\(y=−1\).
الحل
أ- تحتوي المعادلة على متغير واحد فقط،\(x,\)\(x\) وهو دائمًا يساوي\(2.\) إنشاء جدول حيث\(x\) يكون دائمًا\(2\) ثم نضع أي قيم للرسم\(y.\) البياني عبارة عن خط عمودي يمر عبر\(x\) المحور -عند\(2.\)
| \(x\) | \(y\) | \((x,y)\) |
|---|---|---|
| \ (x\)» محول البيانات = «middle">2 | \ (y\)» محول البيانات = «middle">1 | \ ((x, y)\)» data-valign= «middle">\((2,1)\) |
| \ (x\)» محول البيانات = «middle">2 | \ (y\)» محول البيانات = «middle">2 | \ ((x, y)\)» data-valign= «middle">\((2,2)\) |
| \ (x\)» محول البيانات = «middle">2 | \ (y\)» محول البيانات = «middle">3 | \ ((x, y)\)» data-valign= «middle">\((2,3)\) |
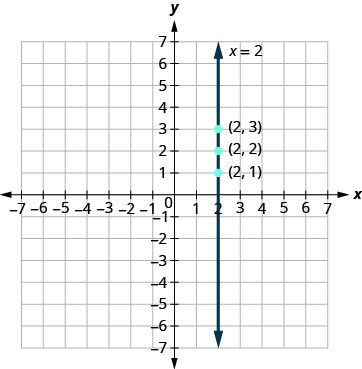
ب- وبالمثل،\(y=−1\) تحتوي المعادلة على متغير واحد فقط،\(y\). القيمة\(y\) ثابتة. جميع الأزواج المرتبة في الجدول التالي لها نفس\(y\) الإحداثيات. الرسم البياني عبارة عن خط أفقي يمر عبر\(y\) المحور -عند\(−1.\)
| \(\mathbf{x}\) | \(\mathbf{ y}\) | \(\mathbf{(x,y)}\) |
|---|---|---|
| \ (\ mathbf {x}\)» محول البيانات = «الأوسط» > 0 | \ (\ mathbf {y}\)» محول البيانات = «middle>»\(−1\) | \ (\ mathbf {(x, y)}\)» داتا-فالين= middle>\((0,−1)\) |
| \ (\ mathbf {x}\)» محول البيانات = «الأوسط» > 3 | \ (\ mathbf {y}\)» محول البيانات = «middle>»\(−1\) | \ (\ mathbf {(x, y)}\)» داتا-فالين= middle>\((3,−1)\) |
| \ (\ mathbf {x}\)» محول البيانات = «middle>»\(−3\) | \ (\ mathbf {y}\)» محول البيانات = «middle>»\(−1\) | \ (\ mathbf {(x, y)}\)» داتا-فالين= middle>\((−3,−1)\) |
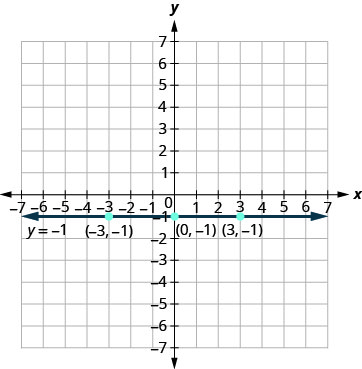
قم برسم المعادلات: أ.\(x=5\) b. \(y=−4\).
- إجابة
-
أ.
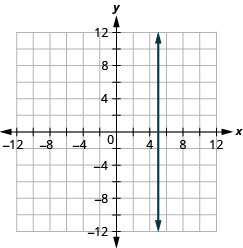
ب.
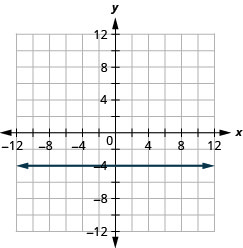
قم برسم المعادلات: أ.\(x=−2\) b. \(y=3\).
- إجابة
-
أ.
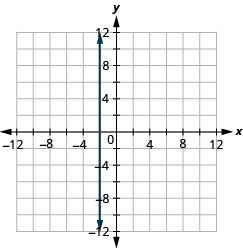
ب.
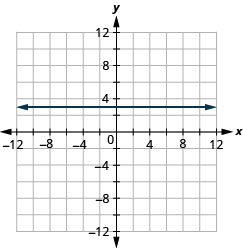
ما الفرق بين المعادلات\(y=4x\) و\(y=4\)؟
\(y=4x\)تحتوي المعادلة\(y.\) على كليهما\(x\)\(y\) وتعتمد القيمة على القيمة\(x,\) لذلك تتغير\(y\) الإحداثيات -وفقًا لقيمة المعادلة التي\(y=4\) تحتوي\(x.\) على متغير واحد فقط. القيمة ثابتة، ولا تعتمد على القيمة،\(x,\) لذلك تكون\(y\) الإحداثيات -conditate دائمًا\(y\)\(4.\)
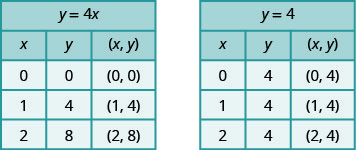
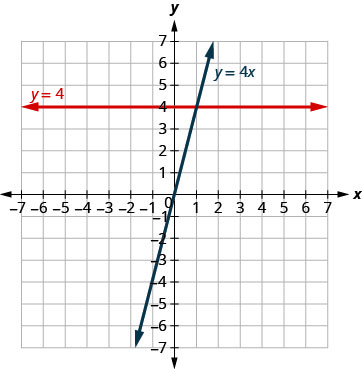
لاحظ، في الرسم البياني، أن المعادلة\(y=4x\) تعطي خطًا مائلًا، بينما\(y=4\) تعطي خطًا أفقيًا.
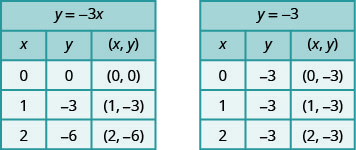
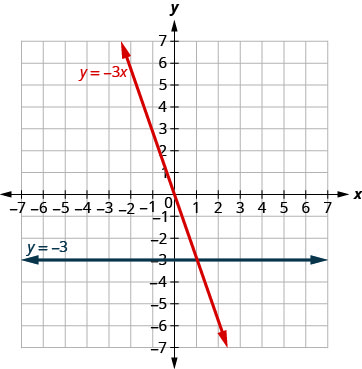
رسم بياني\(y=−3x\)\(y=−3\) وفي نفس نظام الإحداثيات المستطيلة.
الحل:
نلاحظ أن المعادلة الأولى تحتوي على المتغير\(x,\) بينما الثانية لا تحتوي على المتغير. نصنع جدولًا بالنقاط لكل معادلة ثم نرسم الخطوط. يتم عرض الرسمين البيانيين.
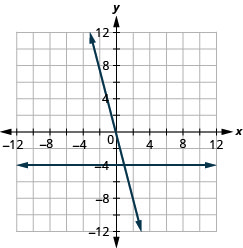
ارسم المعادلات في نفس نظام الإحداثيات المستطيلة:\(y=−4x\) و\(y=−4\).
- إجابة
-
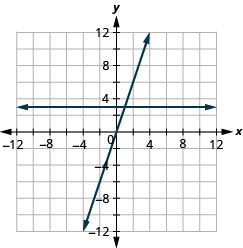
ارسم المعادلات في نفس نظام الإحداثيات المستطيلة:\(y=3\) و\(y=3x\).
- إجابة
-
البحث\(x\)\(y\) - والاعتراض
يمكن تمثيل كل معادلة خطية بخط فريد يعرض جميع حلول المعادلة. لقد رأينا أنه عند رسم خط بياني عن طريق رسم النقاط، يمكنك استخدام أي حلول ثلاثة للرسم البياني. هذا يعني أن شخصين يرسمان الخط قد يستخدمان مجموعات مختلفة من ثلاث نقاط.
للوهلة الأولى، قد لا يبدو الخطان متماثلان، نظرًا لأنه سيكون لهما نقاط مختلفة. ولكن إذا تم تنفيذ جميع الأعمال بشكل صحيح، يجب أن تكون الخطوط هي نفسها تمامًا. تتمثل إحدى طرق التعرف على أنهما بالفعل نفس الخط في النظر إلى المكان الذي يعبر فيه الخط\(x\) المحور\(y\) -والمحور -. تسمى هذه النقاط نقاط اعتراض الخط.
تسمى النقاط التي يعبر فيها الخط\(x\)\(y\) المحور -والمحور -نقاط تقاطع الخط.
دعونا ننظر إلى الرسوم البيانية للخطوط.
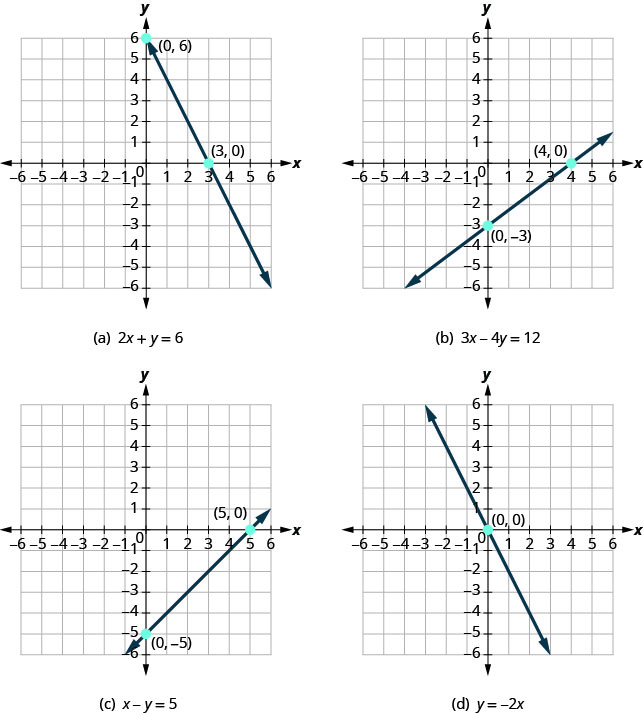
أولاً، لاحظ أين يعبر كل من هذه الخطوط\(x\) المحور -. انظر الجدول.
الآن، دعونا ننظر إلى النقاط التي تعبر فيها هذه الخطوط\(y\) المحور -.
| الشكل | يعبر الخط \(x\) المحور -عند: |
زوج مرتب لهذه النقطة |
يعبر الخط المحور y عند: |
زوج مرتب لهذه النقطة |
|---|---|---|---|---|
| الشكل (أ) | \ (x\) -المحور عند:» data-valign= = middle>\(3\) | \((3,0)\) | \(6\) | \((0,6)\) |
| الشكل (ب) | \ (x\) -المحور عند:» data-valign= = middle>\(4\) | \((4,0)\) | \(−3\) | \((0,−3)\) |
| الشكل (ج) | \ (x\) -المحور عند:» data-valign= = middle>\(5\) | \((5,0)\) | \(−5\) | \((0,5)\) |
| الشكل (د) | \ (x\) -المحور عند:» data-valign= = middle>\(0\) | \((0,0)\) | \(0\) | \((0,0)\) |
| الشكل العام | \ (x\) -المحور عند:» data-valign= = middle>\(a\) | \((a,0)\) | \(b\) | \((0,b)\) |
هل ترى النمط؟
بالنسبة لكل سطر، يكون\(y\) الإحداثي -للنقطة التي يعبر فيها الخط\(x\) المحور -صفرًا. تحتوي النقطة التي يعبر فيها الخط\(x\) المحور -على الشكل\((a,0)\) وتسمى\(x\) -Intercept للخط. يحدث\(x\) التقاطع -عندما يكون\(y\) صفرًا.
في كل سطر، يكون الإحداثي\(x\) - للنقطة التي يعبر فيها الخط\(y\) المحور - صفرًا. تحتوي النقطة التي يعبر فيها الخط\(y\) المحور -على الشكل\((0,b)\) وتسمى\(y\) -Intercept للخط. يحدث\(y\) التقاطع -عندما يكون\(x\) صفرًا.
\(x\)التقاطع -هو النقطة التي يعبر\((a,0)\) فيها الخط\(x\) المحور -.
\(y\)التقاطع -هو النقطة التي يعبر\((0,b)\) فيها الخط\(y\) المحور -.

ابحث عن\(y\) الأجزاء\(x\) - و - في كل رسم بياني معروض.
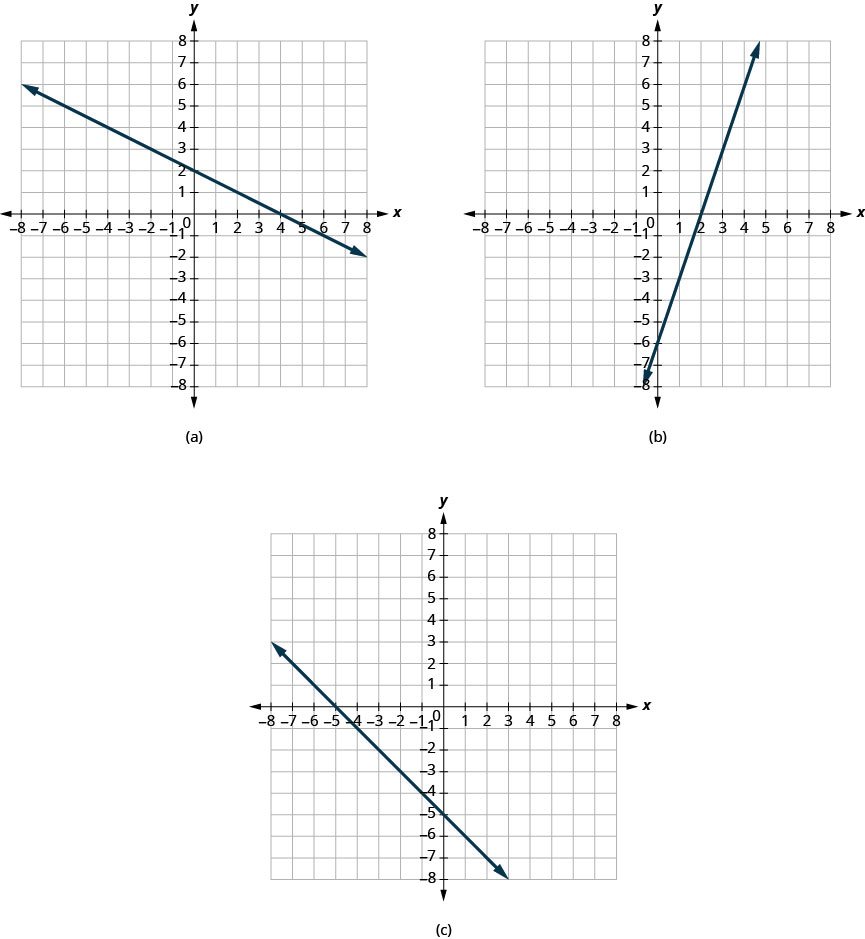
الحل:
أ- يعبر الرسم البياني\(x\) المحور السيني عند النقطة\((4,0)\). التقاطع السيني هو\((4,0)\).
يعبر الرسم البياني\(y\) المحور -عند النقطة\((0,2)\). \(y\)الاعتراض الإلكتروني هو\((0,2)\).
ب- يعبر الرسم البياني\(x\) المحور السيني عند النقطة\((2,0)\). \(x\)الاعتراض الإلكتروني هو\((2,0)\).
يعبر الرسم البياني\(y\) المحور -عند النقطة\((0,−6)\). \(y\)الاعتراض الإلكتروني هو\((0,−6)\).
ج- يعبر الرسم البياني\(x\) المحور السيني عند النقطة\((−5,0)\). \(x\)الاعتراض الإلكتروني هو\((−5,0)\).
يعبر الرسم البياني\(y\) المحور -عند النقطة\((0,−5)\). \(y\)الاعتراض الإلكتروني هو\((0,−5)\).
ابحث عن\(x\) نقاط التقاطع\(y\) - و - على الرسم البياني.
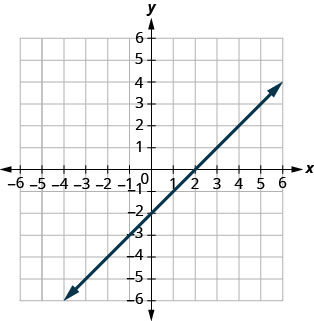
- إجابة
-
\(x\)- الاعتراض:\((2,0)\)،
\(y\) - الاعتراض:\((0,−2)\)
ابحث عن\(x\) نقاط التقاطع\(y\) - و - على الرسم البياني.
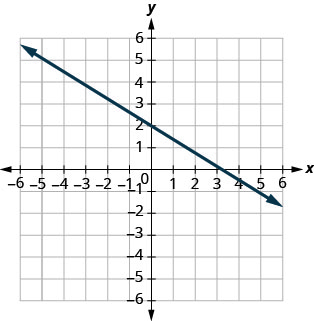
- إجابة
-
\(x\)- الاعتراض:\((3,0)\)،
\(y\) - الاعتراض:\((0,2)\)
إن إدراك أن\(x\) التقاطع -يحدث عندما\(y\) يكون صفرًا وأن\(y\) التقاطع -يحدث عندما\(x\) يكون صفرًا، يعطينا طريقة للعثور على تقاطعات الخط من معادلته. للعثور على\(x\) التقاطع، دعنا\(y=0\) and solve for\(x.\) نعثر على\(y\) التقاطع، دعنا\(x=0\) and solve for\(y.\)
استخدم معادلة الخط. للعثور على:
- \(x\)تقاطع الخط، دعنا\(y=0\) نحلّه\(x\).
- \(y\)تقاطع الخط، دعنا\(x=0\) نحلّه\(y\).
ابحث عن عمليات الاعتراض الخاصة بـ\(2x+y=8\).
الحل:
سنسمح\(y=0\) بالعثور على\(x\) التقاطع، والسماح لنا\(x=0\) بالعثور على\(y\) التقاطع. سنملأ الجدول الذي يذكرنا بما نحتاج إلى العثور عليه.

| للعثور على\(x\) التقاطع، دع\(y=0\). | |
| \(2x+y=8\) | |
| دعونا\(y=0\). | \(2x+{\color{red}0}=8\) |
| قم بالتبسيط. | \(2x=8\) |
| \(x=4\) | |
| \(x\)الاعتراض الإلكتروني هو: | \((4,0)\) |
| للعثور على\(y\) التقاطع، دع\(x=0\). | |
| \(2x+y=8\) | |
| دعونا\(x=0\). | \(2 ( {\color{red}0}) + y = 8\) |
| قم بالتبسيط. | \(0 + y = 8\) |
| \(y=8\) | |
| \(y\)الاعتراض الإلكتروني هو: | \((0,8)\) |
نقاط الاعتراض هي النقاط\((4,0)\)\((0,8)\) وكما هو موضح في الجدول.
| \(2x+y=8\) | |
| \(x\) | \(y\) |
| 4 | 0 |
| 0 | 8 |
ابحث عن عمليات الاعتراض:\(3x+y=12\).
- إجابة
-
\(x\)- الاعتراض:\((4,0)\)،
\(y\) - الاعتراض:\((0,12)\)
ابحث عن عمليات الاعتراض:\(x+4y=8\).
- إجابة
-
\(x\)- الاعتراض:\((8,0)\)،
\(y\) - الاعتراض:\((0,2)\)
ارسم خطًا بيانيًا باستخدام القطع المقطوعة
لرسم معادلة خطية برسم النقاط، تحتاج إلى إيجاد ثلاث نقاط تمثل إحداثياتها حلولًا للمعادلة. يمكنك استخدام نقاط الاعتراض x- و y- كنقطتين من نقاطك الثلاث. ابحث عن نقاط الاعتراض، ثم ابحث عن نقطة ثالثة لضمان الدقة. تأكد من ترتيب النقاط - ثم ارسم الخط. غالبًا ما تكون هذه الطريقة أسرع طريقة لرسم خط.
رسم بياني\(–x+2y=6\) باستخدام عمليات الاعتراض.
الحل:



رسم بياني باستخدام عمليات الاعتراض:\(x–2y=4\).
- إجابة
-
رسم بياني باستخدام عمليات الاعتراض:\(–x+3y=6\).
- إجابة
-
يتم تلخيص خطوات رسم معادلة خطية باستخدام القطع المقطوعة هنا.
- ابحث عن نقاط\(y\) التقاطع\(x\) - و - للخط.
- دع y=0y=0 وقم بحل المشكلة\(x\).
- دع x=0x=0 وقم بحلها\(y\).
- ابحث عن حل ثالث للمعادلة.
- ارسم النقاط الثلاث وتحقق من أنها تصطف.
- ارسم الخط.
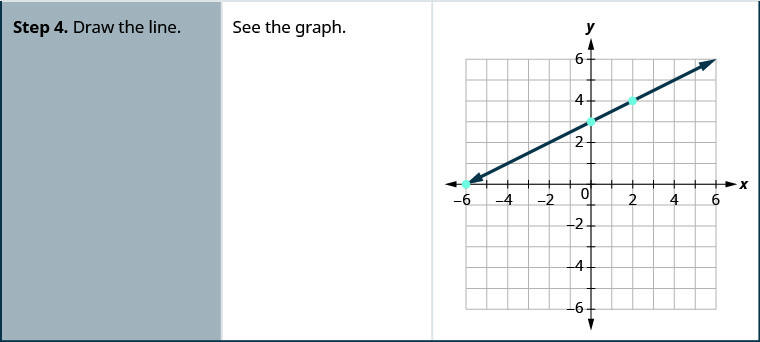
رسم بياني\(4x−3y=12\) باستخدام عمليات الاعتراض.
الحل:
ابحث عن نقاط الاعتراض والنقطة الثالثة.
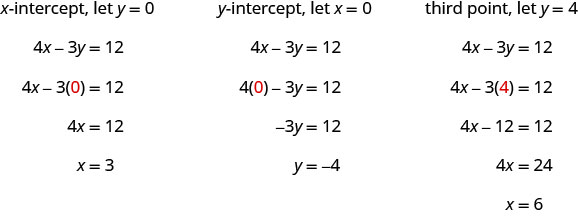
نسرد النقاط في الجدول ونعرض الرسم البياني.
| \(4x−3y=12\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 3 | 0 | \((3,0)\) |
| 0 | \(−4\) | \((0,−4)\) |
| 6 | 4 | \((6,4)\) |
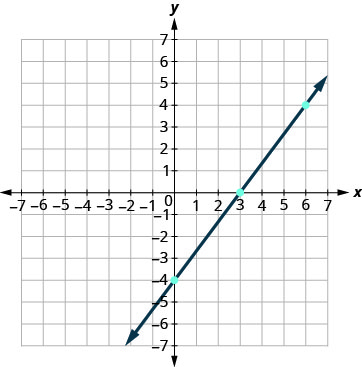
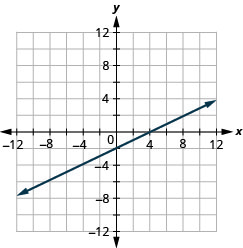
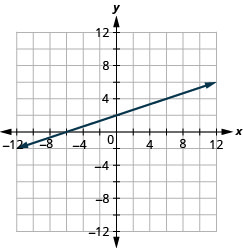
رسم بياني باستخدام عمليات الاعتراض:\(5x−2y=10\).
- إجابة
-
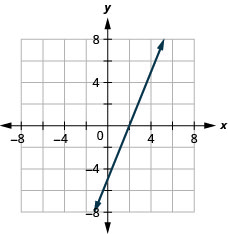
رسم بياني باستخدام عمليات الاعتراض:\(3x−4y=12\).
- إجابة
-
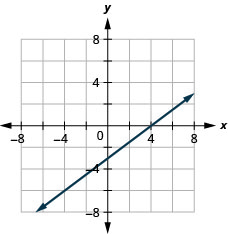
عندما يمر الخط عبر نقطة الأصل، تكون النقطة\(x\) -Intercept و\(y\) -Intercept هي نفس النقطة.
رسم بياني\(y=5x\) باستخدام عمليات الاعتراض.
الحل:

يحتوي هذا الخط على نقطة اعتراض واحدة فقط. إنها النقطة\((0,0)\).
لضمان الدقة، نحتاج إلى رسم ثلاث نقاط. نظرًا لأن\(y\) نقاط التقاطع\(x\) - و -هي نفس النقطة، نحتاج إلى نقطتين إضافيتين لرسم الخط.
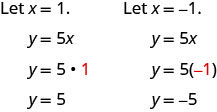
يتم تلخيص النقاط الثلاث الناتجة في الجدول.
| \(y=5x\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 0 | \((0,0)\) |
| 1 | 5 | \((1,5)\) |
| \(−1\) | \(−5\) | \((−1,−5)\) |
ارسم النقاط الثلاث، وتحقق من أنها تصطف، وارسم الخط.
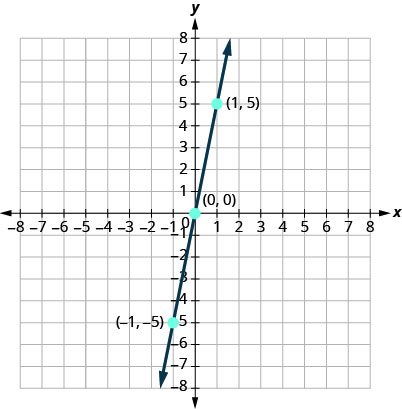
رسم بياني باستخدام عمليات الاعتراض:\(y=4x\).
- إجابة
-
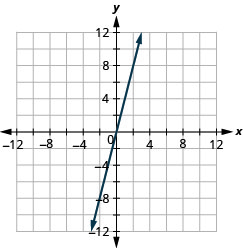
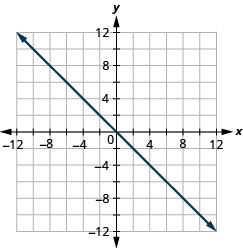
رسم بياني للاعتراضات:\(y=−x\).
- إجابة
-
المفاهيم الرئيسية
- نقاط على المحاور
- النقاط ذات\(y\) الإحداثيات -تساوي\(0\) موجودة على\(x\) المحور -ولها إحداثيات\((a,0)\).
- النقاط ذات\(x\) الإحداثي -يساوي\(0\) وجودها على\(y\) المحور -ولها إحداثيات\((0,b)\).
- رباعي
الربع الأول الربع الثاني الربع الثالث الربع الرابع \((x,y)\) \((x,y)\) \((x,y)\) \((x,y)\) \((+,+)\) \((-,+)\) \((-,-)\) \((+,-)\) 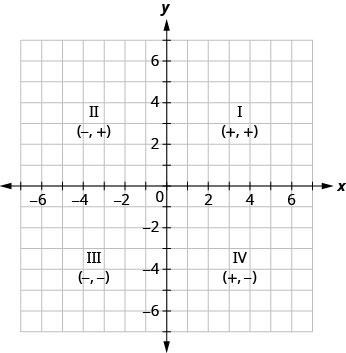
- رسم بياني لمعادلة خطية: الرسم البياني للمعادلة الخطية\(Ax+By=C\) هو خط مستقيم.
كل نقطة على الخط هي حل المعادلة.
كل حل لهذه المعادلة هو نقطة على هذا الخط. - كيفية رسم معادلة خطية برسم النقاط.
- ابحث عن ثلاث نقاط تمثل إحداثياتها حلولًا للمعادلة. قم بتنظيمها في جدول.
- ارسم النقاط في نظام إحداثيات مستطيل. تحقق من أن النقاط تصطف. إذا لم يفعلوا ذلك، تحقق بعناية من عملك.
- ارسم الخط من خلال النقاط الثلاث. قم بتوسيع الخط لملء الشبكة ووضع الأسهم على طرفي الخط.
- \(x\)- اعتراض الخط\(y\) واعتراضه
- \(x\)التقاطع -هو النقطة التي يعبر\((a,0)\) فيها الخط\(x\) المحور -.
- \(y\)التقاطع -هو النقطة التي يعبر\((0,b)\) فيها الخط\(y\) المحور -.

- ابحث عن\(y\) الأجزاء المقطوعة\(x\) - و - من معادلة الخط المستقيم
- استخدم معادلة الخط. للعثور
على:\(x\) التقاطع السيني للخط، دع\(y=0\) المقطع العرضي\(x.\)
للخط\(y\) وقم بحله، ودعه\(x=0\) وحلّه\(y.\)
- استخدم معادلة الخط. للعثور
- كيفية رسم معادلة خطية بيانيًا باستخدام الأجزاء المقطوعة.
- ابحث عن نقاط\(y\) التقاطع\(x\) - و - للخط.
دعونا\(y=0\) نحلّ من أجل «\(x.\)
دعونا\(x=0\) نحلّ»\(y.\) - ابحث عن حل ثالث للمعادلة.
- ارسم النقاط الثلاث وتحقق من أنها تصطف.
- ارسم الخط.
- ابحث عن نقاط\(y\) التقاطع\(x\) - و - للخط.
مسرد المصطلحات
- خط أفقي
- الخط الأفقي هو الرسم البياني لمعادلة الشكل\(y=b.\) الذي يمر به الخط عبر\(y\) المحور -عند\((0,b).\)
- عمليات اعتراض خط
- تسمى النقاط التي يعبر فيها الخط\(x\)\(y\) المحور -والمحور -نقاط تقاطع الخط.
- معادلة خطية
- \(B\)تُسمى معادلة الشكل الذي\(Ax+By=C,\) يكون فيه\(A\) كلاهما صفرًا وليس كلاهما، بالمعادلة الخطية في متغيرين.
- زوج مرتب
- زوج مرتب،\((x,y),\) يعطي إحداثيات نقطة في نظام إحداثيات مستطيل. الرقم الأول هو\(x\) الإحداثيات -. الرقم الثاني هو\(y\) الإحداثيات -.
- أصل
- هذه النقطة\((0,0)\) تسمى الأصل. إنها النقطة التي يتقاطع فيها\(x\) المحور\(y\) -المحور والمحور.
- حل معادلة خطية في متغيرين
- \((x,y)\)يعتبر الزوج المُرتب حلاً للمعادلة الخطية\(Ax+By=C,\) إذا كانت المعادلة عبارة حقيقية عندما يتم استبدال\(y\) القيم\(x\) - و - للزوج المُرتب في المعادلة.
- الشكل القياسي للمعادلة الخطية
- تكون المعادلة الخطية في شكل قياسي عند كتابتها\(Ax+By=C.\)
- خط عمودي
- الخط العمودي هو رسم بياني لمعادلة الشكل. يمر\(x=a.\) الخط عبر\(x\) المحور -عند\((a,0).\)


