2.2: استخدم إستراتيجية عامة لحل المعادلات الخطية
- Page ID
- 201707
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم الخصائص التبادلية والترابطية
- استخدم خصائص الهوية والمعكوس والصفر
- قم بتبسيط التعبيرات باستخدام خاصية التوزيع
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بالتبسيط:\(\frac{3}{2}(12x+20)\).
- قم بالتبسيط:\(5−2(n+1)\).
- ابحث عن شاشة LCD الخاصة بـ\(\frac{5}{6}\) و\(\frac{1}{4}\).
حل المعادلات الخطية باستخدام الإستراتيجية العامة
حل المعادلة يشبه اكتشاف إجابة اللغز. الغرض من حل المعادلة هو العثور على قيمة أو قيم المتغير الذي يجعله بيانًا صحيحًا. أي قيمة للمتغير تجعل المعادلة صحيحة تسمى حلًا للمعادلة. هذا هو الجواب على اللغز!
حل المعادلة هو قيمة المتغير الذي يصنع بيانًا صحيحًا عند استبداله بالمعادلة.
لتحديد ما إذا كان الرقم حلاً لمعادلة، نستبدل قيمة المتغير في المعادلة. إذا كانت المعادلة الناتجة عبارة صحيحة، فإن الرقم هو حل المعادلة.
- استبدل الرقم للمتغير في المعادلة.
- قم بتبسيط التعبيرات على جانبي المعادلة.
- حدد ما إذا كانت المعادلة الناتجة صحيحة.
- إذا كان هذا صحيحًا، فإن الرقم هو الحل.
- إذا لم يكن ذلك صحيحًا، فإن الرقم ليس حلاً.
حدد ما إذا كانت القيم هي حلول للمعادلة:\(5y+3=10y−4\).
- \(y=\frac{3}{5}\)
- \(y=\frac{7}{5}\)
بما أن حل المعادلة هو قيمة المتغير الذي يجعل المعادلة صحيحة، ابدأ باستبدال قيمة الحل للمتغير.
أ.
| \(5 y+3=10 y-4\) | |
| بديل\(\color{rec}\frac{3}{5}\) لـ\(y\) | \(5\left( \color{red} \frac{3}{5} \color{black}\right)+3 \stackrel{?}{=} 10\left( \color{red}\frac{3}{5} \color{black}\right)-4\) |
| اضرب. | \(3+3\stackrel{?}{=} 6-4\) |
| قم بالتبسيط. | \(6 \neq 2\) |
بما أن ذلك\(y=\frac{3}{5}\) لا يؤدي إلى معادلة حقيقية،\(y=\frac{3}{5}\) فهو ليس حلاً للمعادلة\(5y+3=10y−4.\)
ب.
| \(5 y+3=10 y-4\) | |
| بديل\(\color{red} \frac{7}{5}\) لـ\(y\) | \(5\left(\color{red} \frac{7}{5} \color{black}\right)+3 \stackrel{?}{=} 10\left(\color{red}\frac{7}{5}\color{back}\right)-4\) |
| اضرب. | \(7+3 \stackrel{?}{=} 14-4\) |
| قم بالتبسيط. | \(10=10 \checkmark\) |
بما أن\(y=\frac{7}{5}\) النتائج في المعادلة الحقيقية،\(y=\frac{7}{5}\) هي الحل للمعادلة\(5y+3=10y−4.\)
حدد ما إذا كانت القيم عبارة عن حلول للمعادلة:\(9y+2=6y+3.\)
- \(y=\frac{4}{3}\)
- \(y=\frac{1}{3}\)
- الإجابة أ
-
كلا
- الإجابة ب
-
نعم
حدد ما إذا كانت القيم هي حلول للمعادلة:\(4x−2=2x+1\).
- \(x=\frac{3}{2}\)
- \(x=−\frac{1}{2}\)
- الإجابة أ
-
نعم
- الإجابة ب
-
كلا
هناك العديد من أنواع المعادلات التي سنتعلم حلها. سنركز في هذا القسم على المعادلة الخطية.
المعادلة الخطية هي معادلة في متغير واحد يمكن كتابته، حيث\(a\) تكون الأرقام الحقيقية\(a≠0\)، وكما يلي:\(b\)
\[ax+b=0\]
لحل المعادلة الخطية، من الجيد أن يكون لديك استراتيجية شاملة يمكن استخدامها لحل أي معادلة خطية. في المثال التالي، سنقدم خطوات استراتيجية عامة لحل أي معادلة خطية. إن تبسيط كل جانب من المعادلة قدر الإمكان أولاً يجعل بقية الخطوات أسهل.
حل:\(7(n−3)−8=−15\)
- إجابة
-




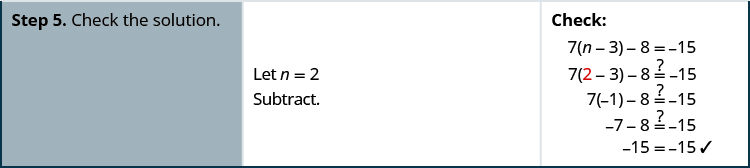
حل:\(2(m−4)+3=−1.\)
- إجابة
-
\(m=2\)
حل:\(5(a−3)+5=−10.\)
- إجابة
-
\(a=0\)
تم تلخيص هذه الخطوات في الإستراتيجية العامة لحل المعادلات الخطية أدناه.
- قم بتبسيط كل جانب من المعادلة قدر الإمكان.
استخدم خاصية التوزيع لإزالة أي أقواس.
اجمع بين المصطلحات المتشابهة. - اجمع كل مصطلحات المتغيرات على جانب واحد من المعادلة.
استخدم خاصية الجمع أو الطرح للمساواة.
- اجمع كل المصطلحات الثابتة على الجانب الآخر من المعادلة.
استخدم خاصية الجمع أو الطرح للمساواة.
- اجعل معامل المصطلح المتغير يساوي 1.
استخدم خاصية الضرب أو القسمة للمساواة.
اذكر حل المعادلة.
- تحقق من الحل.
استبدل الحل بالمعادلة الأصلية للتأكد من أن النتيجة عبارة صحيحة.
حل:\(\frac{2}{3}(3m−6)=5−m\).
- إجابة
-
\(\frac{2}{3}(3 m-6)=5-m\) قم بالتوزيع. \(2 m-4=5-m\) أضف\(m\) إلى كلا الجانبين للحصول على المتغيرات فقط على اليسار. 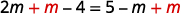
قم بالتبسيط. \(3 m-4=5\) أضف\(4\) إلى كلا الجانبين للحصول على الثوابت فقط على اليمين. 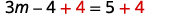
قم بالتبسيط. \(3 m=9\) قسّم كلا الجانبين على ثلاثة. 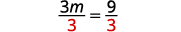
قم بالتبسيط. \(m=3\)
| تحقق من: | 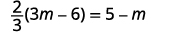 |
| دعونا\(m=3\). | 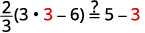 |
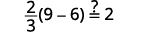 |
|
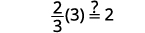 |
|
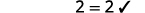 |
حل:\(\frac{1}{3}(6u+3)=7−u\).
- إجابة
-
\(u=2\)
حل:\(\frac{2}{3}(9x−12)=8+2x\).
- إجابة
-
\(x=4\)
يمكننا حل المعادلات عن طريق الحصول على جميع مصطلحات المتغيرات على جانبي علامة التساوي. من خلال جمع المصطلحات المتغيرة على الجانب الذي يكون فيه معامل المتغير أكبر، نتجنب العمل مع بعض السلبيات. ستكون هذه استراتيجية جيدة عندما نحل عدم المساواة لاحقًا في هذا الفصل. كما أنه يساعدنا على منع الأخطاء مع السلبيات.
حل:\(4(x−1)−2=5(2x+3)+6\).
- إجابة
-
\(4(x-1)-2=5(2 x+3)+6\) قم بالتوزيع. \(4 x-4-2=10 x+15+6\)
اجمع بين المصطلحات المتشابهة. \(4 x-6=10 x+21\) اطرح\(4x\) من كل جانب للحصول على المتغيرات على اليمين فقط منذ ذلك الحين\(10>4\). \(4 x \color{red} -4 \color{black} x-6=10 x \color{red}-4 x \color{black}+21\) قم بالتبسيط. \(-6=6 x+21\) اطرح\(21\) من كل جانب للحصول على الثوابت على اليسار. \(-6 \color{red} -21 \color{black} =6 x+21 \color{red}-21\)
قم بالتبسيط. \(-27=6 x\) قسّم كلا الجانبين على\(6\). \(\frac{-27}{\color{red}6} \color{black}=\frac{6 x}{\color{red}6}\) قم بالتبسيط. \(-\frac{9}{2}=x\) تحقق من: \(4(x-1)-2=5(2 x+3)+6\)\) دعونا\(x=−92\). 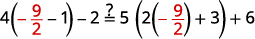
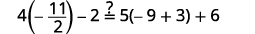
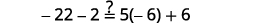
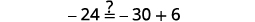
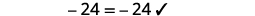
حل:\(6(p−3)−7=5(4p+3)−12.\)
- إجابة
-
\(p=−2\)
حل:\(8(q+1)−5=3(2q−4)−1.\)
- إجابة
-
\(q=−8\)
حل:\(10[3−8(2s−5)]=15(40−5s)\).
- إجابة
-
\(10[3-8(2 s-5)]=15(40-5 s)\) قم بالتبسيط من الأقواس الداخلية أولاً. \(10[3-16 s+40]=15(40-5 s)\) ادمج المصطلحات المتشابهة في الأقواس. \(10[43-16 s]=15(40-5 s)\) قم بالتوزيع. \(430-160 s=600-75 s\) أضف\(160s\) إلى كلا الجانبين للحصول\(160s\) على كلا الجانبين للحصول على المتغيرات إلى اليمين. 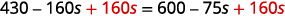
قم بالتبسيط. \(430=600+85 s\) اطرح\(600\) من كلا الجانبين للحصول على الثوابت على اليسار. 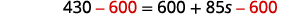
قم بالتبسيط. \(-170=85 s\) قسّم كلا الجانبين على\(85\). 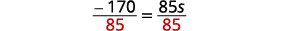
قم بالتبسيط. \(-2=s,\)وبالتالي\(s = -2\) تحقق من: \(10[3-8(2 s-5)]=15(40-5 s)\) دعونا\(s=−2\). 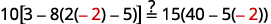
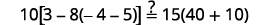
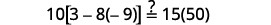
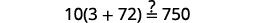
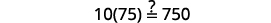
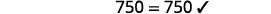
حل:\(6[4−2(7y−1)]=8(13−8y)\).
- إجابة
-
\(y=−\frac{17}{5}\)
حل:\(12[1−5(4z−1)]=3(24+11z).\)
- إجابة
-
\(z=0\)
تصنيف المعادلات
يعتمد ما إذا كانت المعادلة صحيحة أم لا على قيمة المتغير. تكون المعادلة\(7x+8=−13\) صحيحة عندما نستبدل المتغير، x، بالقيمة\(−3\)، ولكنها ليست صحيحة عندما نستبدل x بأي قيمة أخرى. معادلة كهذه تسمى المعادلة الشرطية. جميع المعادلات التي قمنا بحلها حتى الآن هي معادلات شرطية.
المعادلة الصحيحة لقيمة واحدة أو أكثر من قيم المتغير والخاطئة لجميع القيم الأخرى للمتغير هي معادلة شرطية.
الآن دعونا ننظر في المعادلة\(7y+14=7(y+2)\). هل تدرك أن الجانب الأيسر والجانب الأيمن متساويان؟ دعونا نرى ما يحدث عندما نحلها لـ y.
حل:
| \(7 y+14=7(y+2)\) | |
| قم بالتوزيع. | \(7 y+14=7 y+14\) |
| اطرح\(7y\) على كل جانب للحصول على\(y’\) s على جانب واحد. | \(7 y \color{red}-7 y \color{black} +14=7 y \color{red} -7 y \color{black}+14\) |
| البساطة -\(y\) يتم التخلص منها. | \(14=14\) |
| لكن\(14=14\) هذا صحيح. |
هذا يعني أن المعادلة\(7y+14=7(y+2)\) صحيحة لأي قيمة لـ\(y\). نقول أن حل المعادلة هو جميع الأرقام الحقيقية. المعادلة التي تنطبق على أي قيمة للمتغير تسمى الهوية.
المعادلة التي تنطبق على أي قيمة للمتغير تسمى الهوية.
حل الهوية صالح لجميع الأرقام الحقيقية.
ماذا يحدث عندما نحل المعادلة\(−8z=−8z+9?\)
حل:
| \(-8 z=-8 z+9\) | |
| أضف\(8z\) إلى كلا الجانبين لترك الثابت بمفرده على اليمين. | \(-8 z \color{red} +8 z \color{black}=-8 z \color{red}+8 z \color{black} +9\) |
| البساطة -\(z\) يتم التخلص منها. | \(0 \neq 9\) |
| لكن\(0≠9\). |
حل المعادلة\(−8z=−8z+9\) أدى إلى العبارة الخاطئة\(0=9\). \(−8z=−8z+9\)لن تكون المعادلة صحيحة لأي قيمة من\(z\). ليس لديها حل. تسمى المعادلة التي لا تحتوي على حل، أو التي تكون خاطئة لجميع قيم المتغير، بالتناقض.
تسمى المعادلة الخاطئة لجميع قيم المتغير بالتناقض.
التناقض ليس له حل.
ستطلب منا الأمثلة القليلة التالية تصنيف المعادلة على أنها مشروطة أو هوية أو كتناقض.
صنف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(6(2n−1)+3=2n−8+5(2n+1)\).
- إجابة
-
\(6(2 n-1)+3=2 n-8+5(2 n+1)\) قم بالتوزيع. \(12 n-6+3=2 n-8+10 n+5\) اجمع بين المصطلحات المتشابهة. \(12 n-3=12 n-3\) اطرح\(12n\) من كل جانب للحصول على الحرف\(n\) على جانب واحد. 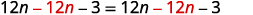
قم بالتبسيط. \(-3=-3\) هذا بيان حقيقي. المعادلة هي هوية. الحل هو جميع الأرقام الحقيقية.
صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(4+9(3x−7)=−42x−13+23(3x−2).\)
- إجابة
-
الهوية؛ جميع الأرقام الحقيقية
صنّف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1.\)
- إجابة
-
الهوية؛ جميع الأرقام الحقيقية
صنف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(8+3(a−4)=0\).
- إجابة
-
\(8+3(a-4)=0\) قم بالتوزيع. \(8+3 a-12=0\) اجمع بين المصطلحات المتشابهة. \(3 a-4=0\) أضف\(4\) إلى كلا الجانبين. \(3 a-4 \color{red}+4 \color{black}=0 \color{red}+4\) قم بالتبسيط. \(3 a=4\) يقسم. \(\frac{3 a}{\color{red}3} \color{black}=\frac{4}{\color{red}3}\) قم بالتبسيط. \(a=\frac{4}{3}\) تكون المعادلة صحيحة عندما\(a=\frac{4}{3}\). هذه معادلة شرطية. الحل هو\(a=\frac{4}{3}\).
صنف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(11(q+3)−5=19\).
- إجابة
-
معادلة شرطية؛\(q=−\frac{9}{11}\)
صنف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(6+14(k−8)=95\).
- إجابة
-
معادلة شرطية؛\(k=\frac{201}{14}\)
صنف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(5m+3(9+3m)=2(7m−11)\).
- إجابة
-
\(5 m+3(9+3 m)=2(7 m-11)\) قم بالتوزيع. \(5 m+27+9 m=14 m-22\) اجمع بين المصطلحات المتشابهة. \(14 m+27=14 m-22\) اطرح\(14m\) من كلا الجانبين. \(14 m+27 \color{red}-14 m \color{black}=14 m-22 \color{red}-14 m\) قم بالتبسيط. \(27 \neq-22\) لكن\(27≠−22\). المعادلة عبارة عن تناقض. ليس لديها حل.
صنف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(12c+5(5+3c)=3(9c−4)\).
- إجابة
-
تناقض؛ لا يوجد حل
صنف المعادلة كمعادلة شرطية أو هوية أو تناقض ثم حدد الحل:\(4(7d+18)=13(3d−2)−11d\).
- إجابة
-
تناقض؛ لا يوجد حل
نلخص طرق تصنيف المعادلات في الجدول.
| نوع المعادلة | ماذا يحدث عند حلها؟ | الحل |
|---|---|---|
| معادلة شرطية | صحيح لقيمة واحدة أو أكثر من المتغيرات وخطأ لجميع القيم الأخرى | قيمة واحدة أو أكثر |
| الهوية | صحيح لأي قيمة للمتغير | جميع الأرقام الحقيقية |
| التناقض | خطأ لجميع قيم المتغير | لا يوجد حل |
حل المعادلات باستخدام معاملات الكسر أو الأعداد العشرية
يمكننا استخدام الإستراتيجية العامة لحل المثال التالي. ستعمل هذه الطريقة بشكل جيد، لكن العديد من الطلاب لا يشعرون بثقة كبيرة عندما يرون كل هذه الكسور. لذلك، سوف نعرض طريقة بديلة لحل المعادلات بالكسور. تزيل هذه الطريقة البديلة الكسور.
سوف نطبق خاصية الضرب للمساواة ونضرب كلا طرفي المعادلة في المقام المشترك الأصغر (LCD) لجميع الكسور في المعادلة. ستكون نتيجة هذه العملية معادلة جديدة، تعادل الأولى، ولكن بدون كسور. هذه العملية تسمى مسح معادلة الكسور.
لمسح معادلة الأعداد العشرية، نفكر في جميع الأعداد العشرية في صورة الكسر الخاصة بها ثم نجد شاشة LCD لهذه المقامات.
حل:\(\frac{1}{12}x+\frac{5}{6}=\frac{3}{4}\).
- إجابة
-



حل:\(\frac{1}{4}x+\frac{1}{2}=\frac{5}{8}\).
- إجابة
-
\(x=\frac{1}{2}\)
حل:\(\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}\).
- إجابة
-
\(x=−2\)
لاحظ في المثال السابق أنه بمجرد مسح معادلة الكسور، كانت المعادلة مثل تلك التي قمنا بحلها سابقًا في هذا الفصل. لقد غيرنا المشكلة إلى مشكلة عرفنا بالفعل كيفية حلها. ثم استخدمنا الإستراتيجية العامة لحل المعادلات الخطية.
- ابحث عن المقام المشترك الأصغر (LCD) لجميع الكسور والأعداد العشرية (في شكل كسر) في المعادلة.
- اضرب كلا طرفي المعادلة في شاشة LCD هذه. يؤدي ذلك إلى مسح الكسور والأرقام العشرية.
- حل باستخدام الإستراتيجية العامة لحل المعادلات الخطية.
حل:\(5=\frac{1}{2}y+\frac{2}{3}y−\frac{3}{4}y\).
- إجابة
-
نريد مسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD لجميع الكسور في المعادلة.
ابحث عن شاشة LCD لجميع الكسور في المعادلة. \(5=\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\) شاشة ال سي دي هي\(12\). اضرب كلا طرفي المعادلة في\(12\). \(\color{red}12 \color{black}(5)=\color{red}12 \color{black} \cdot\left(\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\right)\) قم بالتوزيع. \(12(5)=12 \cdot \frac{1}{2} y+12 \cdot \frac{2}{3} y-12 \cdot \frac{3}{4} y\) التبسيط - لاحظ عدم وجود المزيد من الكسور. \(60=6 y+8 y-9 y\) اجمع بين المصطلحات المتشابهة. \(60=5 y\) اقسم على خمسة. \(\frac{60}{\color{red}5} \color{black}=\frac{5 y}{\color{red}5}\) قم بالتبسيط. \(12=y\) تحقق من: \(5=\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\) دعونا\(y=12\). 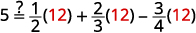
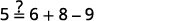

حل:\(7=\frac{1}{2}x+\frac{3}{4}x−\frac{2}{3}x\).
- إجابة
-
\(x=12\)
حل:\(−1=\frac{1}{2}u+\frac{1}{4}u−\frac{2}{3}u\).
- إجابة
-
\(u=−12\)
في المثال التالي، سنقوم بالتوزيع قبل مسح الكسور.
حل:\(\frac{1}{2}(y−5)=\frac{1}{4}(y−1)\).
- إجابة
-
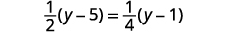
قم بالتوزيع. 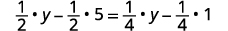
قم بالتبسيط. 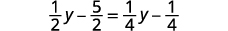
اضرب في شاشة LCD، أربعة. 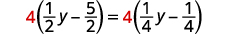
قم بالتوزيع. 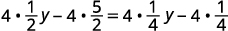
قم بالتبسيط. 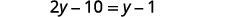
اجمع المتغيرات على اليسار. 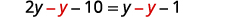
قم بالتبسيط. 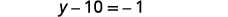
اجمع الثوابت على اليمين. 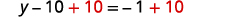
قم بالتبسيط. 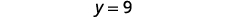
هناك طريقة بديلة لحل هذه المعادلة وهي مسح الكسور دون التوزيع أولاً. إذا قمت بضرب العوامل بشكل صحيح، فستكون هذه الطريقة أسهل. 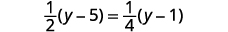
اضرب على شاشة LCD،\(4\). 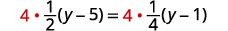
اضرب أربعة أضعاف الكسور. 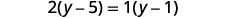
قم بالتوزيع. 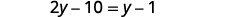
اجمع المتغيرات على اليسار. 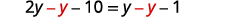.jpg)
قم بالتبسيط. 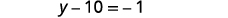
اجمع الثوابت على اليمين. 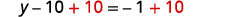
قم بالتبسيط. 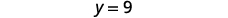
تحقق من: 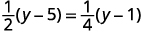
دعونا\(y=9\). 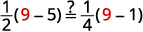
قم بإنهاء الفحص بنفسك.
حل:\(\frac{1}{5}(n+3)=\frac{1}{4}(n+2)\).
- إجابة
-
\(n=2\)
حل:\(\frac{1}{2}(m−3)=\frac{1}{4}(m−7)\).
- إجابة
-
\(m=−1\)
عندما تقوم بضرب كلا طرفي المعادلة في شاشة LCD الخاصة بالكسور، تأكد من ضرب كل حد في LCD - حتى إذا كان لا يحتوي على كسر.
حل:\(\frac{4q+3}{2}+6=\frac{3q+5}{4}\)
- إجابة
-
\(\frac{4 q+3}{2}+6=\frac{3 q+5}{4}\) اضرب كلا الجانبين في شاشة LCD،\(4\). 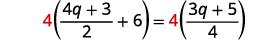
قم بالتوزيع. 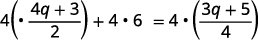
قم بالتبسيط. \(2(4 q+3)+24=3 q+5\) \(8 q+6+24=3 q+5\) \(8 q+30=3 q+5\) اجمع المتغيرات على اليسار. 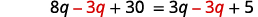
قم بالتبسيط. \(5 q+30=5\) اجمع الثوابت على اليمين. 
قم بالتبسيط. \(5 q=-25\) قسّم كلا الجانبين على خمسة. 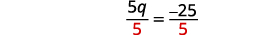
قم بالتبسيط. \(q=-5\) تحقق من: \(\frac{4 q+3}{2}+6=\frac{3 q+5}{4}\) دع\(q=−5.\) 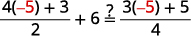
قم بإنهاء الفحص بنفسك.
حل:\(\frac{3r+5}{6}+1=\frac{4r+3}{3}\).
- إجابة
-
\(r=3\)
حل:\(\frac{2s+3}{2}+1=\frac{3s+2}{4}\).
- إجابة
-
\(s=−8\)
تحتوي بعض المعادلات على أعداد عشرية. قد يحدث هذا النوع من المعادلات عندما نحل مشاكل تتعلق بالمال أو النسب المئوية. ولكن يمكن أيضًا التعبير عن الأرقام العشرية ككسور. على سبيل المثال،\(0.7=\frac{7}{10}\) و\(0.29=\frac{29}{100}\). لذلك، باستخدام المعادلة ذات الأعداد العشرية، يمكننا استخدام نفس الطريقة التي استخدمناها لمسح الكسور - ضرب كلا طرفي المعادلة في المقام المشترك الأصغر.
يستخدم المثال التالي معادلة نموذجية لتلك التي سنراها في تطبيقات النقود في قسم لاحق. لاحظ أننا سنقوم بمسح جميع الأرقام العشرية بالضرب في شاشة LCD الخاصة بنموذج الكسر الخاص بها.
حل:\(0.25x+0.05(x+3)=2.85\).
- إجابة
-
انظر إلى الأعداد العشرية وفكر في الكسور المتكافئة:
\[0.25=\frac{25}{100}, \; \; \; \;\;\;\;\; 0.05=\frac{5}{100}, \;\;\;\;\;\;\;\; 2.85=2\frac{85}{100}.\]
لاحظ أن شاشة LCD هي\(100\). بالضرب في شاشة LCD، سنمسح الأرقام العشرية من المعادلة.
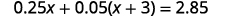
قم بالتوزيع أولاً. 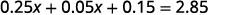
اجمع بين المصطلحات المتشابهة. 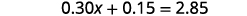
لمسح الأعداد العشرية، اضرب في\(100\). 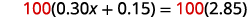
قم بالتوزيع. 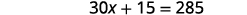
اطرح\(15\) من كلا الجانبين. 
قم بالتبسيط. 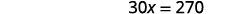
اقسم على\(30\). 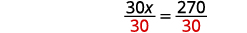
قم بالتبسيط. 
تحقق من ذلك بنفسك عن طريق الاستبدال\(x=9\) بالمعادلة الأصلية.
حل:\(0.25n+0.05(n+5)=2.95.\)
- إجابة
-
\(n=9\)
حل:\(0.10d+0.05(d−5)=2.15.\)
- إجابة
-
\(d=16\)
المفاهيم الرئيسية
- كيفية تحديد ما إذا كان الرقم هو الحل للمعادلة
- استبدل الرقم في للمتغير في المعادلة.
- قم بتبسيط التعبيرات على جانبي المعادلة.
- حدد ما إذا كانت المعادلة الناتجة صحيحة.
إذا كان هذا صحيحًا، فإن الرقم هو الحل.
إذا لم يكن ذلك صحيحًا، فإن الرقم ليس حلاً.
- كيفية حل المعادلات الخطية باستخدام استراتيجية عامة
- قم بتبسيط كل جانب من المعادلة قدر الإمكان.
استخدم خاصية التوزيع لإزالة أي أقواس.
اجمع بين المصطلحات المتشابهة.
- اجمع كل مصطلحات المتغيرات على جانب واحد من المعادلة.
استخدم خاصية الجمع أو الطرح للمساواة.
- اجمع كل المصطلحات الثابتة على الجانب الآخر من المعادلة.
استخدم خاصية الجمع أو الطرح للمساواة.
- اجعل معامل المصطلح المتغير يساوي 1.
استخدم خاصية الضرب أو القسمة للمساواة.
اذكر حل المعادلة.
- تحقق من الحل.
استبدل الحل بالمعادلة الأصلية للتأكد من أن النتيجة عبارة صحيحة.
- قم بتبسيط كل جانب من المعادلة قدر الإمكان.
- كيفية حل المعادلات ذات المعاملات الكسرية أو العشرية
- ابحث عن المقام المشترك الأصغر (LCD) لجميع الكسور والأعداد العشرية (في شكل كسر) في المعادلة.
- اضرب كلا طرفي المعادلة في شاشة LCD هذه. يؤدي ذلك إلى مسح الكسور والأرقام العشرية.
- حل باستخدام الإستراتيجية العامة لحل المعادلات الخطية.
مسرد المصطلحات
- معادلة شرطية
- المعادلة الصحيحة لقيمة واحدة أو أكثر من قيم المتغير والخاطئة لجميع القيم الأخرى للمتغير هي معادلة شرطية.
- تناقض
- تسمى المعادلة الخاطئة لجميع قيم المتغير بالتناقض. التناقض ليس له حل.
- هوية
- المعادلة التي تنطبق على أي قيمة للمتغير تسمى الهوية. حل الهوية هو كل الأرقام الحقيقية.
- معادلة خطية
- المعادلة الخطية هي معادلة في متغير واحد يمكن كتابته، حيث a و b عبارة عن أرقام حقيقية و\(a≠0\)، as\(ax+b=0\).
- حل المعادلة
- حل المعادلة هو قيمة المتغير الذي يصنع بيانًا صحيحًا عند استبداله بالمعادلة.


