1.2: استخدم لغة الجبر
- Page ID
- 201558
في نهاية هذا القسم، ستكون قادرًا على:
- ابحث عن العوامل والعوامل الأولية والمضاعفات الأقل شيوعًا
- استخدم المتغيرات والرموز الجبرية
- قم بتبسيط التعبيرات باستخدام ترتيب العمليات
- تقييم تعبير
- تحديد المصطلحات المتشابهة ودمجها
- ترجمة عبارة إنجليزية إلى تعبير جبري
يهدف هذا الفصل إلى أن يكون مراجعة موجزة للمفاهيم التي ستكون مطلوبة في دورة الجبر المتوسط. يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي تم تناولها في هذا الفصل في فصل الجبر الأولي، الأسس.
ابحث عن العوامل والعوامل الأولية والمضاعفات الشائعة الأقل
تسمى الأرقام 2، 4، 6، 8، 10، 12 مضاعفات 2. يمكن كتابة مضاعف 2 كمنتج لرقم العد و2.
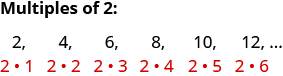
وبالمثل، فإن مضاعف 3 سيكون نتاج رقم العد و3.

يمكننا العثور على مضاعفات أي رقم من خلال متابعة هذه العملية.
| رقم العد | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| مضاعفات 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| مضاعفات 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| مضاعفات 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| مضاعفات 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| مضاعفات 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| مضاعفات 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| مضاعفات 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| مضاعفات 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
الرقم هو مضاعف\(n\) إذا كان نتاج رقم العد و\(n\).
هناك طريقة أخرى للقول بأن 15 هو مضاعف 3 وهي القول بأن 15 قابل للقسمة على 3. هذا يعني أنه عندما نقسم 3 إلى 15، نحصل على رقم العد. في الواقع،\(15÷3\) هو\(5\)، كذلك\(15\)\(5⋅3\).
إذا كان الرقم\(m\) مضاعفًا لـ\(n\)،\(m\) فيمكن القسمة على\(n\).
إذا أردنا البحث عن أنماط في مضاعفات الأرقام من 2 إلى 9، فسوف نكتشف اختبارات القسمة التالية:
الرقم قابل للقسمة على:
- 2 إذا كان الرقم الأخير هو 0 أو 2 أو 4 أو 6 أو 8.
- 3 إذا كان مجموع الأرقام قابلاً للقسمة على 3.
- 5 إذا كان الرقم الأخير هو 5 أو 0.
- 6 إذا كانت قابلة للقسمة على كل من 2 و 3.
- 10 إذا انتهى بـ 0.
هل 5,625 قابل للقسمة على
- 2؟
- 3؟
- 5 أو 10؟
- 6؟
- إجابة
-
أ.
\(\text{Is 5,625 divisible by 2?}\)
\( \begin{array}{ll} \text{Does it end in 0, 2, 4, 6 or 8?} & {\text{No.} \\ \text{5,625 is not divisible by 2.}} \end{array}\) - ب.
\(\text{5,625 divisible by 3?}\)
\(\begin{array}{ll} {\text{What is the sum of the digits?} \\ \text{Is the sum divisible by 3?}} & {5+6+2+5=18 \\ \text{Yes.} \\ \text{5,625 is divisible by 3.}}\end{array}\) - ج.
\(\text{Is 5,625 divisible by 5 or 10?}\)
\(\begin{array}{ll} \text{What is the last digit? It is 5.} & \text{5,625 is divisible by 5 but not by 10.} \end{array}\)د.\(\text{Is 5,625 divisible by 6?}\)
\(\begin{array}{ll}\text{Is it divisible by both 2 and 3?} & {\text{No, 5,625 is not divisible by 2, so 5,625 is} \\ \text{not divisible by 6.}} \end{array}\)
هل يمكن قسمة 4962 على أ. 2؟ ب. 3؟ ج. 5؟ د. 6؟ هاء. 10؟
- إجابة
-
أ. نعم ب. نعم ج. لا د. نعم هـ.
هل يمكن قسمة 3765 على أ. 2؟ ب. 3؟ ج. 5؟ د. 6؟ هاء. 10؟
- إجابة
-
أ. لا ب. نعم ج. نعم د. لا ه.
في الرياضيات، غالبًا ما تكون هناك عدة طرق للتحدث عن نفس الأفكار. حتى الآن، رأينا أنه إذا كان\(m\) مضاعفًا لـ\(n\)، يمكننا القول\(m\) أنه يمكن القسمة عليه\(n\). على سبيل المثال، بما أن 72 هو مضاعف 8، نقول أن 72 قابل للقسمة على 8. نظرًا لأن 72 هو مضاعف 9، نقول أن 72 قابل للقسمة على 9. يمكننا التعبير عن هذا بطريقة أخرى.
نظرًا\(8·9=72\) لأننا نقول أن 8 و 9 هما عاملان من عوامل 72. عندما نكتب\(72=8·9\)، نقول أننا أخذنا في الاعتبار 72.
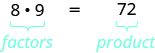
طرق أخرى للعمل\(72\) هي\(1·72, \; 2·36, \; 3·24, \; 4·18,\) و\(6⋅12\). الرقم 72 له العديد من العوامل:\(1,\,2,\,3,\,4,\,6,\,8,\,9,\,12,\,18,\,24,\,36,\) و\(72\).
إذا\(b\) كنت\(a\) تقوم بحساب الأرقام\(a·b=m\)،\(a\) ثم\(b\) هي عوامل\(m\).
تحتوي بعض الأرقام، مثل 72، على العديد من العوامل. الأرقام الأخرى لها عاملان فقط. العدد الأولي هو رقم عد أكبر من 1 ومعامله الوحيدة هي 1 ونفسه.
العدد الأولي هو رقم عد أكبر من 1 ومعامله الوحيدة هي 1 والرقم نفسه.
الرقم المركب هو رقم عد ليس أوليًا. يحتوي الرقم المركب على عوامل أخرى غير 1 والرقم نفسه.
يتم سرد أرقام العد من 2 إلى 20 في الجدول مع عواملها. تأكد من الموافقة على التسمية «الأولية» أو «المركبة» لكل منها!
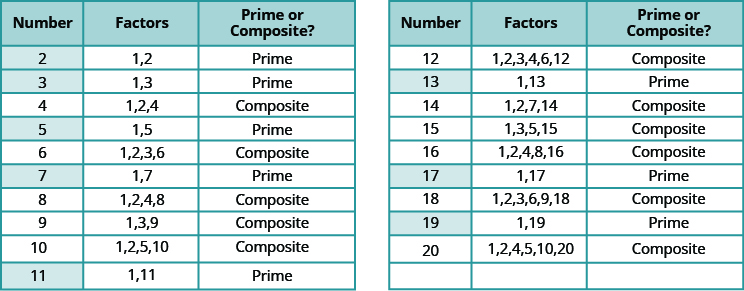
الأعداد الأولية الأقل من 20 هي 2 و3 و5 و7 و11 و13 و17 و19. لاحظ أن الرقم الأولي الزوجي الوحيد هو 2.
يمكن كتابة رقم مركب كمنتج فريد من الأعداد الأولية. وهذا ما يسمى التحليل الأولي للرقم. سيكون العثور على التحليل الأولي لعدد مركب مفيدًا في العديد من الموضوعات في هذه الدورة.
إن التحليل الأولي للرقم هو حاصل ضرب الأعداد الأولية التي تساوي العدد.
للعثور على التحليل الأولي لعدد مركب، ابحث عن أي عاملين للعدد واستخدمهما لإنشاء فرعين. إذا كان العامل أساسيًا، يكون هذا الفرع مكتملًا. ضع دائرة حول هذا الجزء الرئيسي وإلا فمن السهل أن تفقد الأرقام الأولية.
إذا لم يكن العامل أوليًا، فابحث عن عاملين للعدد وتابع العملية. بمجرد أن تكون جميع الفروع محاطة بدائرة في النهاية، يكتمل التحليل. يمكن الآن كتابة الرقم المركب كمنتج للأرقام الأولية.
العامل 48.
- إجابة
-


.jpg)
نقول\(2⋅2⋅2⋅2⋅3\) هو التحليل الأولي لـ 48. نكتب بشكل عام الأعداد الأولية بترتيب تصاعدي. تأكد من مضاعفة العوامل للتحقق من إجابتك. \(2⋅2⋅2⋅2⋅3\)هو التحليل الأولي لـ 48. نكتب بشكل عام الأعداد الأولية بترتيب تصاعدي. تأكد من مضاعفة العوامل للتحقق من إجابتك.
إذا أخذنا في الاعتبار 48 لأول مرة بطريقة مختلفة، على سبيل المثال\(6·8\)، ستظل النتيجة كما هي. قم بإنهاء التحليل الأولي وتحقق من ذلك بنفسك.
ابحث عن التحليل الأولي لـ\(80\).
- إجابة
-
\(2⋅2⋅2⋅2⋅5\)
ابحث عن التحليل الأولي لـ\(60\).
- إجابة
-
\(2⋅2⋅3⋅5\)
- ابحث عن عاملين يكون منتجهما هو الرقم المعطى، واستخدم هذه الأرقام لإنشاء فرعين.
- إذا كان العامل أساسيًا، يكون هذا الفرع مكتملًا. ضع دائرة حول الجزء الرئيسي، مثل ورقة على الشجرة.
- إذا لم يكن العامل أساسيًا، فاكتبه كمنتج لعاملين واستمر في العملية.
- اكتب العدد المركب في صورة حاصل ضرب كل الأعداد الأولية المحاطة بدائرة.
أحد الأسباب التي تجعلنا ننظر إلى الأعداد الأولية هو استخدام هذه التقنيات للعثور على المضاعف المشترك الأقل لعددين. سيكون هذا مفيدًا عندما نجمع ونطرح الكسور ذات المقامات المختلفة.
المضاعف المشترك الأصغر (LCM) لرقمين هو أصغر رقم هو مضاعف كلا الرقمين.
للعثور على المضاعف المشترك الأقل لعددين، سنستخدم طريقة Prime Factors. دعونا نجد LCM لـ 12 و 18 باستخدام عواملها الأولية.
ابحث عن المضاعف المشترك الأصغر (LCM) للعددين ١٢ و١٨ باستخدام طريقة العوامل الأولية.
- إجابة
-

.jpg)


لاحظ أن العوامل الرئيسية لـ 12\((2·2·3)\) والعوامل الرئيسية لـ 18\((2⋅3⋅3)\) مدرجة في LCM\((2·2·3·3)\). لذا فإن 36 هو المضاعف الأقل شيوعًا لـ 12 و 18.
من خلال مطابقة الأعداد الأولية الشائعة، يتم استخدام كل عامل رئيسي مشترك مرة واحدة فقط. بهذه الطريقة تكون متأكدًا من أن 36 هو المضاعف الأقل شيوعًا.
ابحث عن LCM للعدد ٩ و١٢ باستخدام طريقة العوامل الأولية.
- إجابة
-
36
ابحث عن LCM للعددين ١٨ و٢٤ باستخدام طريقة العوامل الأولية.
- إجابة
-
72
- اكتب كل رقم في صورة نتاج الأعداد الأولية.
- ضع قائمة بالأعداد الأولية لكل رقم. قم بمطابقة الأعداد الأولية عموديًا عند الإمكان.
- انزل الأعمدة.
- اضرب العوامل.
استخدم المتغيرات والرموز الجبرية
في الجبر، نستخدم حرفًا من الأبجدية لتمثيل رقم قد تتغير قيمته. نسمي هذا المتغير والحروف المستخدمة بشكل شائع للمتغيرات هي\(x,\,y,\,a,\,b,\) و\(c.\)
المتغير هو حرف يمثل رقمًا قد تتغير قيمته.
يُطلق على الرقم الذي تظل قيمته دائمًا كما هي اسم الثابت.
الثابت هو الرقم الذي تظل قيمته دائمًا كما هي.
للكتابة جبريًا، نحتاج إلى بعض رموز العمليات بالإضافة إلى الأرقام والمتغيرات. هناك عدة أنواع من الرموز التي سنستخدمها. هناك أربع عمليات حسابية أساسية: الجمع والطرح والضرب والقسمة. سنقوم بإدراج الرموز المستخدمة للإشارة إلى هذه العمليات أدناه.
| عملية | الترميز | قل: | النتيجة هي... |
|---|---|---|---|
| إضافة | \(a+b\) | \(a\)زائد\(b\) | مجموع\(a\) و\(b\) |
| الطرح | \(a−b\) | \(a\)ناقص\(b\) | الفرق بين\(a\) و\(b\) |
| عملية الضرب | \(a⋅b,\,ab,\,(a)(b),\,(a)b,\,a(b)\) | \(a\)مرات\(b\) | منتج من\(a\) و\(b\) |
| توزيع | \(a÷b,\,\space a/b,\,\space\frac{a}{b},\,\space b \overline{\smash{)}a}\) | \(a\)مقسومًا على\(b\) | حاصل\(a\) القسمة\(b\)؛ \(a\) يسمى العائد،\(b\) ويسمى المقسوم |
عندما تكون الكميتان لهما نفس القيمة، نقول أنهما متساويان ونربطهما بعلامة متساوية.
\(a=b\)تتم قراءة "\(a\)يساوي»\(b\).
الرمز «\(=\)» يسمى علامة المساواة.
في خط الأعداد، تصبح الأرقام أكبر عندما تنتقل من اليسار إلى اليمين. يمكن استخدام خط الأرقام لشرح الرموز «\(<\)» و «\(>\)».

\(a>b\)يمكن قراءة التعبيرات\(a<b\) من اليسار إلى اليمين أو من اليمين إلى اليسار، على الرغم من أننا عادة ما نقرأ باللغة الإنجليزية من اليسار إلى اليمين. بشكل عام،
\[a<b \text{ is equivalent to }b>a. \text{For example, } 7<11 \text{ is equivalent to }11>7.\]
\[a>b \text{ is equivalent to }b<a. \text{For example, } 17>4 \text{ is equivalent to }4<17.\]
| رموز عدم المساواة | كلمات |
|---|---|
| \(a\neq b\) | \(a\)لا يساوي\(b\). |
| \(a<b\) | \(a\)أقل من\(b\). |
| \(a\leq b\) | \(a\)أقل من أو يساوي\(b\). |
| \(a>b\) | \(a\)أكبر من\(b\). |
| \(a\geq b\) | \(a\)أكبر من أو يساوي\(b\). |
رموز التجميع في الجبر تشبه إلى حد كبير الفواصل والنقطتين وعلامات الترقيم الأخرى في اللغة الإنجليزية. فهي تساعد في تحديد التعبير الذي يمكن أن يتكون من رقم أو متغير أو مجموعة من الأرقام والمتغيرات باستخدام رموز التشغيل. سنقدم ثلاثة أنواع من رموز التجميع الآن.
\[\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\]
فيما يلي بعض الأمثلة على التعبيرات التي تتضمن رموز التجميع. سنقوم بتبسيط التعبيرات مثل هذه لاحقًا في هذا القسم.
\[8(14−8) \qquad 21−3[2+4(9−8)] \qquad 24÷ \{13−2[1(6−5)+4]\}\]
ما الفرق في اللغة الإنجليزية بين العبارة والجملة؟ تعبر العبارة عن فكرة واحدة غير مكتملة في حد ذاتها، لكن الجملة تقدم بيانًا كاملاً. تحتوي الجملة على موضوع وفعل. في الجبر، لدينا تعبيرات ومعادلات.
التعبير هو رقم أو متغير أو مزيج من الأرقام والمتغيرات باستخدام رموز التشغيل.
\[\begin{array}{lll} \textbf{Expression} & \textbf{Words} & \textbf{English Phrase} \\ \mathrm{3+5} & \text{3 plus 5} & \text{the sum of three and five} \\ \mathrm{n−1} & n\text{ minus one} & \text{the difference of } n \text{ and one} \\ \mathrm{6·7} & \text{6 times 7} & \text{the product of six and seven} \\ \frac{x}{y} & x \text{ divided by }y & \text{the quotient of }x \text{ and }y \end{array} \]
لاحظ أن العبارات الإنجليزية لا تشكل جملة كاملة لأن العبارة لا تحتوي على فعل.
المعادلة هي تعبيران مرتبطان بعلامة تساوي. عندما تقرأ الكلمات التي تمثلها الرموز في المعادلة، يكون لديك جملة كاملة باللغة الإنجليزية. تعطي علامة المساواة الفعل.
المعادلة عبارة عن تعبيرين متصلين بعلامة تساوي.
\[\begin{array}{ll} \textbf{Equation} & \textbf{English Sentence} \\ 3+5=8 & \text{The sum of three and five is equal to eight.} \\ n−1=14 & n \text{ minus one equals fourteen.} \\ 6·7=42 & \text{The product of six and seven is equal to forty-two.} \\ x=53 & x \text{ is equal to fifty-three.} \\ y+9=2y−3 & y \text{ plus nine is equal to two } y \text{ minus three.} \end{array}\]
لنفترض أننا بحاجة إلى ضرب 2 تسع مرات. يمكننا كتابة هذا كـ\(2·2·2·2·2·2·2·2·2\). هذا أمر شاق وقد يكون من الصعب تتبع كل هذه الـ 2 ثانية، لذلك نستخدم الأسس. نكتب\(2·2·2\) كما\(\mathrm{2^3}\)\(2·2·2·2·2·2·2·2·2\) وباسم\(2^9\). في تعبيرات مثل\(2^3\)، يُطلق على 2 اسم الأساس بينما يُطلق على 3 اسم الأس. يخبرنا الأس عن عدد المرات التي نحتاج فيها إلى ضرب القاعدة.

نقول\(2^3\) هو بالرمز الأسي\(2·2·2\) وهو في تدوين موسع.
\(a^n\)يعني مضاعفة\(n\) عوامل الرقم\(a\).
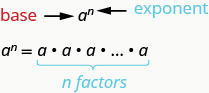
\(a^n\)يتم قراءة التعبير\(a\) إلى\(n^{th}\) السلطة.
\(a^n\)بينما نقرأ\(“a\) عن «\(n^{th}\)القوة»، نقرأ عادةً:
\[\begin{array}{cc} a^2 & “a \text{ squared}” \\ a^3 & “a \text{ cubed}” \end{array}\]
سنرى لاحقًا لماذا\(a^2\)\(a^3\) ولدينا أسماء خاصة.
يوضح الجدول كيف نقرأ بعض التعبيرات ذات الأسس.
| التعبير | في الكلمات | |
|---|---|---|
| 7 2 | 7 إلى القوة الثانية أو | 7 مربع |
| 5 3 | 5 إلى القوة الثالثة أو | 5 مكعبات |
| 9 4 | 9 إلى القوة الرابعة | |
| 12 5 | 12 إلى القوة الخامسة |
تبسيط التعبيرات باستخدام ترتيب العمليات
إن تبسيط التعبير يعني القيام بكل العمليات الحسابية الممكنة. على سبيل المثال، للتبسيط،\(\mathrm{4·2+1}\) سنضرب أولاً\(\mathrm{4⋅2}\) للحصول على 8 ثم نضيف 1 للحصول على 9. من العادات الجيدة التي يجب تطويرها العمل على الصفحة وكتابة كل خطوة من العملية أسفل الخطوة السابقة. سيبدو المثال الموصوف للتو كما يلي:
\[ 4⋅2+1 \\ 8+1 \\ 9\]
من خلال عدم استخدام علامة المساواة عند تبسيط التعبير، يمكنك تجنب الخلط بين التعبيرات والمعادلات.
لتبسيط التعبير، قم بإجراء جميع العمليات في التعبير.
لقد قدمنا معظم الرموز والرموز المستخدمة في الجبر، ولكننا الآن بحاجة إلى توضيح ترتيب العمليات. وإلا، قد يكون للتعبيرات معاني مختلفة، وقد تؤدي إلى قيم مختلفة.
على سبيل المثال، ضع في اعتبارك التعبير\(4+3⋅7\). يقوم بعض الطلاب بتبسيط عملية الحصول على 49، عن طريق إضافة هذه النتيجة\(4+3\) ثم ضربها في 7. يحصل الآخرون على 25، عن طريق الضرب\(3·7\) أولاً ثم إضافة 4.
يجب أن يعطي نفس التعبير نفس النتيجة. لذلك وضع علماء الرياضيات بعض الإرشادات التي تسمى ترتيب العمليات.
- الأقواس ورموز التجميع الأخرى
- قم بتبسيط جميع التعبيرات داخل الأقواس أو رموز التجميع الأخرى، مع العمل على الأقواس الداخلية أولاً.
- أسس أسس
- قم بتبسيط جميع التعبيرات باستخدام الأسس.
- الضرب والقسمة
- قم بإجراء جميع عمليات الضرب والقسمة بالترتيب من اليسار إلى اليمين. هذه العمليات لها أولوية متساوية.
- الجمع والطرح
- قم بإجراء جميع عمليات الجمع والطرح بالترتيب من اليسار إلى اليمين. هذه العمليات لها أولوية متساوية.
غالبًا ما يسأل الطلاب، «كيف سأتذكر الطلب؟» إليك طريقة لمساعدتك على التذكر: خذ الحرف الأول من كل كلمة رئيسية واستبدل العبارة السخيفة «يرجى المعذرة عزيزتي عمتي سالي».
\[\begin{array}{ll} \text{Parentheses} & \text{Please} \\ \text{Exponents} & \text{Excuse} \\ \text{Multiplication Division} & \text{My Dear} \\ \text{Addition Subtraction} & \text{Aunt Sally} \end{array}\]
من الجيد أن تتوافق عبارة «My y De ear» معًا، لأن هذا يذكرنا بأن الضرب وقسم الإعلانات الخاص بي لهما أولوية متساوية. لا نقوم دائمًا بالضرب قبل القسمة أو نقوم دائمًا بالقسمة قبل الضرب. نقوم بها بالترتيب من اليسار إلى اليمين.
وبالمثل، فإن عبارة «A unt S ally» تتوافق معًا وتذكرنا بأن الإصدار والطرح لهما أيضًا أولوية متساوية ونقوم بهما بالترتيب من اليسار إلى اليمين.
قم بالتبسيط:\(18÷6+4(5−2)\).
- إجابة
-
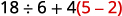
أقواس؟ نعم، اطرح أولاً. 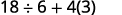
أسس؟ لا. الضرب أو القسمة؟ نعم. قسّم أولاً لأننا نضرب ونقسم من اليسار إلى اليمين. 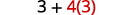
أي ضرب أو تقسيم آخر؟ نعم. اضرب. 
أي ضرب آخر للقسمة؟ لا. أي إضافة أو طرح؟ نعم. أضف. 
قم بالتبسيط:\(30÷5+10(3−2).\)
- إجابة
-
16
قم بالتبسيط:\(70÷10+4(6−2).\)
- إجابة
-
23
عندما تكون هناك رموز تجميع متعددة، نقوم بتبسيط الأقواس الداخلية أولاً ونعمل للخارج.
قم بالتبسيط:\(5+2^3+3[6−3(4−2)].\)
- إجابة
-
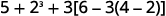
هل هناك أي أقواس (أو رموز تجميع أخرى)؟ نعم. 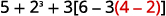
ركز على الأقواس الموجودة داخل الأقواس. اطرح. 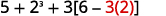
استمر داخل الأقواس واضرب. 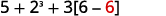
استمر داخل الأقواس واسحب. 
لا يتطلب التعبير الموجود داخل الأقواس مزيدًا من التبسيط. هل هناك أي أسس؟ نعم. قم بتبسيط الأسس. 
هل هناك أي ضرب أو تقسيم؟ نعم. اضرب. 
هل هناك أي إضافة للطرح؟ نعم. أضف. 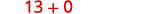
أضف. 
قم بالتبسيط:\(9+5^3−[4(9+3)].\)
- إجابة
-
86
قم بالتبسيط:\(7^2−2[4(5+1)].\)
- إجابة
-
1
تقييم تعبير
في الأمثلة القليلة الأخيرة، قمنا بتبسيط التعبيرات باستخدام ترتيب العمليات. سنقوم الآن بتقييم بعض التعبيرات - مرة أخرى باتباع ترتيب العمليات. تقييم التعبير يعني العثور على قيمة التعبير عندما يتم استبدال المتغير برقم معين.
تقييم التعبير يعني العثور على قيمة التعبير عندما يتم استبدال المتغير برقم معين.
لتقييم تعبير، استبدل هذا الرقم بالمتغير في التعبير ثم قم بتبسيط التعبير.
قم بالتقييم عندما\(x=4\): أ.\(x^2\) ب.\(3^x\) ج\(2x^2+3x+8\).
- إجابة
-
أ.
ب.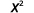
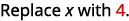

استخدم تعريف الأس. 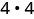
قم بالتبسيط. 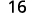
ج.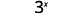
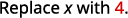

استخدم تعريف الأس. 
قم بالتبسيط. 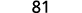
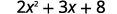
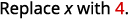
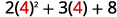
اتبع ترتيب العمليات. .jpg)
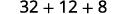
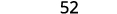
قم بتقييم متى\(x=3\)، أ.\(x^2\) ب.\(4^x\) ج\(3x^2+4x+1\).
- إجابة
-
أ. 9
ب. 64
ج. 40
قم بتقييم متى\(x=6\)، أ.\(x^3\) ب.\(2^x\) ج\(6x^2−4x−7\).
- إجابة
-
(أ) 216
(ب) 64
(ج) 185
تحديد المصطلحات المتشابهة ودمجها
تتكون التعبيرات الجبرية من مصطلحات. المصطلح هو ثابت، أو نتاج ثابت ومتغير واحد أو أكثر.
المصطلح هو ثابت أو نتاج ثابت ومتغير واحد أو أكثر.
أمثلة على المصطلحات هي\(7,\,y,\,5x^2,\,9a,\) و\(b^5\).
يسمى الثابت الذي يضاعف المتغير بالمعامل.
معامل المصطلح هو الثابت الذي يضرب المتغير في المصطلح.
فكر في المعامل كرقم أمام المتغير. معامل المصطلح\(3x\) هو 3. عندما نكتب\(x\)، يكون المعامل هو 1، منذ ذلك الحين\(x=1⋅x\).
تشترك بعض المصطلحات في سمات مشتركة. عندما يكون المصطلحان ثوابت أو لهما نفس المتغير والأس، فإننا نقول أنهما يشبهان المصطلحات.
انظر إلى المصطلحات الستة التالية. أي منها يبدو أن لديها سمات مشتركة؟
\[5x \quad 7 \quad n^2 \quad 4 \quad 3x \quad 9n^2\]
نحن نقول،
\(7\)\(4\)وهي مثل المصطلحات.
\(5x\)\(3x\)وهي مثل المصطلحات.
\(n^2\)\(9n^2\)وهي مثل المصطلحات.
المصطلحات التي تكون إما ثوابت أو لها نفس المتغيرات المرفوعة إلى نفس القوى تسمى المصطلحات المتشابهة.
إذا كانت هناك مصطلحات متشابهة في التعبير، يمكنك تبسيط التعبير من خلال دمج المصطلحات المتشابهة. نضيف المعاملات ونحافظ على نفس المتغير.
\[\begin{array}{lc} \text{Simplify.} & 4x+7x+x \\ \text{Add the coefficients.} & 12x \end{array}\]
قم بالتبسيط:\(2x^2+3x+7+x^2+4x+5\).
- إجابة
-



قم بالتبسيط:\(3x^2+7x+9+7x^2+9x+8\).
- إجابة
-
\(10x^2+16x+17\)
قم بالتبسيط:\(4y^2+5y+2+8y^2+4y+5.\)
- إجابة
-
\(12y^2+9y+7\)
- حدد المصطلحات المشابهة.
- أعد ترتيب التعبير بحيث تكون المصطلحات معًا.
- قم بإضافة المعاملات أو طرحها واحتفظ بنفس المتغير لكل مجموعة من المصطلحات المتشابهة.
ترجمة عبارة إنجليزية إلى تعبير جبري
قمنا بإدراج العديد من رموز العمليات المستخدمة في الجبر. الآن، سنستخدمها لترجمة العبارات الإنجليزية إلى تعبيرات جبرية. ستساعدنا الرموز والمتغيرات التي تحدثنا عنها في القيام بذلك. يلخص الجدول هذه العناصر.
| عملية | عبارة | التعبير |
|---|---|---|
| إضافة | \(a\)زائد\(b\)
مجموع\(a\) و\(b\) \(a\)زاد بمقدار\(b\) \(b\)أكثر من\(a\) إجمالي\(a\) و\(b\) \(b\)أضيف إلى\(a\) |
\(a+b\) |
| الطرح | \(a\)ناقص\(b\)
الفرق بين\(a\) و\(b\) \(a\)انخفض بمقدار\(b\) \(b\)أقل من\(a\) \(b\)مخصوم من\(a\) |
\(a−b\) |
| عملية الضرب | \(a\)مرات\(b\)
منتج من\(a\) و\(b\) مرتين\(a\) |
\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\) |
| قسم | \(a\)مقسومًا على\(b\)
حاصل القسمة من\(a\) و\(b\) نسبة\(a\) و\(b\) \(b\)مقسمة إلى\(a\) |
\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\) |
انظر عن كثب إلى هذه العبارات باستخدام العمليات الأربع:

تخبرنا كل عبارة بالعمل على رقمين. ابحث عن كلمات و للعثور على الأرقام.
تخبرنا كل عبارة بالعمل على رقمين. ابحث عن كلمات و للعثور على الأرقام.
ترجم كل عبارة إنجليزية إلى تعبير جبري:
أ. الفرق بين\(14x\) و\(9\)
ب. حاصل\(8y^2\) القسمة\(3\)ج. أكثر من اثني عشر\(y\)
د. سبعة أقل من\(49x^2\)
- إجابة
-
أ. الكلمة الرئيسية هي الاختلاف، الذي يخبرنا أن العملية هي الطرح. ابحث عن كلمات and and t للعثور على الأرقام المراد طرحها.
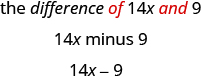
ب- الكلمة الرئيسية هي حاصل القسمة، الذي يخبرنا أن العملية هي القسمة.

ج. الكلمات الرئيسية هي أكثر من. يخبروننا أن العملية هي إضافة. أكثر من عبارة «تمت الإضافة إلى».
\[\text{twelve more than }y \\ \text{twelve added to }y \\ y+12\]
د. الكلمات الرئيسية أقل من. يقولون لنا أن نطرح. أقل من يعني «مخصوم من».
\[\text{seven less than }49x^2 \\ \text{seven subtracted from }49x^2 \\ 49x^2−7\]
ترجم العبارة الإنجليزية إلى تعبير جبري:
أ. الفرق بين\(14x^2\) و\(13\)
ب. حاصل\(12x\) القسمة\(2\)
ج.\(13\) أكثر من\(z\)
د.\(18\) أقل من\(8x\)
- إجابة
-
أ.\(14x^2−13\) ب.\(12x÷2\)
ج.\(z+13\) د.\(8x−18\)
ترجم العبارة الإنجليزية إلى تعبير جبري:
أ. مجموع\(17y^2\) و\(19\)
ب. منتج من\(7\) و\(y\)
(ج) أكثر من أحد عشر\(x\)
(د) أقل بأربعة عشر من\(11a\)
- إجابة
-
أ.\(17y^2+19\) ب.\(7y\)
ج.\(x+11\) د.\(11a−14\)
نحن ننظر بعناية إلى الكلمات لمساعدتنا على التمييز بين ضرب المجموع وإضافة منتج.
ترجم العبارة الإنجليزية إلى تعبير جبري:
أ. ثمانية أضعاف مجموع\(x\) و\(y\)
ب. مجموع ثماني مرات\(x\) و\(y\)
- إجابة
-
هناك كلمتان عمليتان - تخبرنا الأوقات بالضرب والمجموع يخبرنا بالجمع.
أ- لأننا\(8\) نضرب المجموع، نحتاج إلى أقواس حول مجموع\(x\) و\(y\)،\((x+y)\). هذا يجبرنا على تحديد المبلغ أولاً. (تذكر ترتيب العمليات.)
\[\text{eight times the sum of }x \text{ and }y \\ 8(x+y)\]
ب- لأخذ المبلغ، نبحث عن كلمات و ونرى ما تتم إضافته. نحن هنا نأخذ مجموع ثماني مرات\(x\) و\(y\).
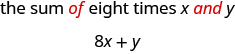
ترجم العبارة الإنجليزية إلى تعبير جبري:
أ. أربعة أضعاف مجموع\(p\) و\(q\)
ب. مجموع أربع مرات\(p\) و\(q\)
- إجابة
-
أ.\(4(p+q)\) ب.\(4p+q\)
ترجم العبارة الإنجليزية إلى تعبير جبري:
أ. الفرق بين مرتين\(x\) و\(8\)
ب. ضعف الفرق بين\(x\) و\(8\)
- إجابة
-
أ.\(2x−8\) ب.\(2(x−8)\)
في وقت لاحق من هذه الدورة، سنقوم بتطبيق مهاراتنا في الجبر لحل التطبيقات. ستكون الخطوة الأولى هي ترجمة عبارة إنجليزية إلى تعبير جبري. سنرى كيفية القيام بذلك في المثالين التاليين.
يقل طول المستطيل بمقدار 14 عن العرض. دعونا\(w\) نمثل عرض المستطيل. اكتب مقدارًا يُعبِّر عن طول المستطيل.
- إجابة
-
\[\begin{array}{lc} \text{Write a phrase about the length of the rectangle.} & \text{14 less than the width} \\ \text{Substitute }w \text{ for “the width.”} & w \\ \text{Rewrite less than as subtracted from.} & \text{14 subtracted from } w \\ \text{Translate the phrase into algebra.} & w−14 \end{array}\]
يقل طول المستطيل عن العرض بمقدار 7. دعونا\(w\) نمثل عرض المستطيل. اكتب مقدارًا يُعبِّر عن طول المستطيل.
- إجابة
-
\(w−7\)
عرض المستطيل\(6\) أقل من الطول. دعونا\(l\) نمثل طول المستطيل. اكتب تعبيرًا لعرض المستطيل.
- إجابة
-
\(l−6\)
سيتم استخدام التعبيرات في المثال التالي في مشاكل خليط العملات النموذجية التي سنراها قريبًا.
يونيو لديها الدايمات والأرباع في حقيبتها. يقل عدد الدايمات بسبعة عن أربعة أضعاف عدد الأرباع. دعونا\(q\) نمثل عدد الأرباع. اكتب مقدارًا يُعبِّر عن عدد الدايمات.
- إجابة
-
\[\begin{array}{lc} \text{Write a phrase about the number of dimes.} & \text{7 less than 4 times }q \\ \text{Translate 4 times }q. & \text{7 less than 4}q \\ \text{Translate the phrase into algebra.} & 4q−7 \end{array}\]
جيفري لديه الدايمات والأرباع في جيبه. يقل عدد الدايمات بثمانية أضعاف عن أربعة أضعاف عدد الأرباع. دعونا\(q\) نمثل عدد الأرباع. اكتب مقدارًا يُعبِّر عن عدد الدايمات.
- إجابة
-
\(4q−8\)
لورين لديها الدايمات والنيكل في حقيبتها. يزيد عدد الدايمات بثلاثة أضعاف عن سبعة أضعاف عدد النيكل. دعونا\(n\) نمثل عدد النيكل. اكتب مقدارًا يُعبِّر عن عدد الدايمات.
- إجابة
-
\(7n+3\)
المفاهيم الرئيسية
- اختبارات
القسمة يمكن تقسيم الرقم على:
2 إذا كان الرقم الأخير هو 0 أو 2 أو 4 أو 6 أو 8.
3 إذا كان مجموع الأرقام قابلاً للقسمة على 3.
5 إذا كان الرقم الأخير هو 5 أو 0.
6 إذا كانت قابلة للقسمة على كل من 2 و 3.
10 إذا انتهى بـ 0. - كيفية العثور على التحليل الأولي لعدد مركب.
- ابحث عن عاملين يكون منتجهما هو الرقم المعطى، واستخدم هذه الأرقام لإنشاء فرعين.
- إذا كان العامل أساسيًا، يكون هذا الفرع مكتملًا. ضع دائرة حول البرايم، مثل برعم على الشجرة.
- إذا لم يكن العامل أساسيًا، فاكتبه كمنتج لعاملين واستمر في العملية.
- اكتب العدد المركب في صورة حاصل ضرب كل الأعداد الأولية المحاطة بدائرة.
- كيفية العثور على المضاعف الأقل شيوعًا باستخدام طريقة العوامل الأولية.
- اكتب كل رقم في صورة نتاج الأعداد الأولية.
- ضع قائمة بالأعداد الأولية لكل رقم. قم بمطابقة الأعداد الأولية عموديًا عند الإمكان.
- انزل الأعمدة.
- اضرب العوامل.
\(a=b\)تتم قراءة رمز المساواة «\(a\)يساوي»\(b\). يسمى الرمز «=» علامة المساواة.
- رموز عدم المساواة
رموز عدم المساواة كلمات \(a≠b\) \(a\)لا يساوي\(b\). \(a<b\) \(a\)أقل من\(b\). \(a≤b\) \(a\)أقل من أو يساوي\(b\). \(a>b\) \(a\)أكبر من\(b\). \(a≥b\) \(a\)أكبر من أو يساوي \(b\). - رموز التجميع\(\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\)
- الترميز الأسي\(a^n\) يعني الضرب \(a\)بحد ذاته، \(n\)مرات. يتم قراءة \(a\)التعبير «an»\(n^{th}\) للسلطة.
- تبسيط تعبير
لتبسيط التعبير، قم بجميع العمليات في التعبير. - كيفية استخدام ترتيب العمليات.
- الأقواس ورموز التجميع الأخرى
- قم بتبسيط جميع التعبيرات داخل الأقواس أو رموز التجميع الأخرى، مع العمل على الأقواس الداخلية أولاً.
- أسس أسس
- قم بتبسيط جميع التعبيرات باستخدام الأسس.
- الضرب والقسمة
- قم بإجراء جميع عمليات الضرب والقسمة بالترتيب من اليسار إلى اليمين. هذه العمليات لها أولوية متساوية.
- الجمع والطرح
- قم بإجراء جميع عمليات الجمع والطرح بالترتيب من اليسار إلى اليمين. هذه العمليات لها أولوية متساوية.
- الأقواس ورموز التجميع الأخرى
- كيفية الجمع بين المصطلحات المتشابهة.
- حدد المصطلحات المشابهة.
- أعد ترتيب التعبير بحيث تكون المصطلحات معًا.
- قم بإضافة المعاملات أو طرحها واحتفظ بنفس المتغير لكل مجموعة من المصطلحات المتشابهة.
عملية عبارة التعبير إضافة \(a\)بالإضافة \(b\)
إلى مجموع \(a\)\(b\)
\(a\)وزيادة \(b\)
\(b\)بأكثر من\(a\)
المجموع \(a\)\(b\)
\(b\)والإضافة إلى\(a\)\(a+b\) الطرح \(a\)ناقص \(b\)
الفرق\(a\) \(b\)
\(a\)والنقص \(b\)
\(b\)بأقل من\(a\)
\(b\)مخصوم من\(a\)\(a−b\) عملية الضرب \(a\)أضعاف \(b\)
المنتج \(a\)\(b\)
ومرتين\(a\)\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\)
قسم \(a\)مقسومًا على \(b\)
حاصل القسمة من \(a\)و \(b\)
نسبة \(a\)و \(b\)
\(b\)مقسمة إلى\(a\)\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\)
مسرد المصطلحات
- معامل في الرياضيات او درجة
- معامل المصطلح هو الثابت الذي يضرب المتغير في المصطلح.
- رقم مركب
- الرقم المركب هو رقم عد ليس أوليًا. لديها عوامل أخرى غير 1 والرقم نفسه.
- ثابت
- الثابت هو الرقم الذي تظل قيمته دائمًا كما هي.
- قابل للقسمة على رقم
- إذا كان الرقم \(m\)مضاعفًا لـ \(n\)، \(m\)فيمكن القسمة على \(n\).
- معادلة
- المعادلة عبارة عن تعبيرين متصلين بعلامة تساوي.
- تقييم تعبير
- تقييم التعبير يعني العثور على قيمة التعبير عندما يتم استبدال المتغيرات برقم معين.
- التعبير
- التعبير هو رقم أو متغير أو مزيج من الأرقام والمتغيرات باستخدام رموز التشغيل.
- العوامل
- إذا\(a·b=m\)، إذن \(a\)، وما \(b\)هي عوامل \(m\).
- المضاعف المشترك الأقل
- المضاعف المشترك الأصغر (LCM) لرقمين هو أصغر رقم هو مضاعف كلا الرقمين.
- مثل المصطلحات
- المصطلحات التي تكون إما ثوابت أو لها نفس المتغيرات المرفوعة إلى نفس القوى تسمى المصطلحات المتشابهة.
- مضاعف عدد
- الرقم هو مضاعف \(n\)إذا كان نتاج رقم العد و \(n\).
- ترتيب العمليات
- ترتيب العمليات عبارة عن إرشادات ثابتة لتبسيط التعبير.
- التحليل الأولي
- إن التحليل الأولي للرقم هو حاصل ضرب الأعداد الأولية التي تساوي العدد.
- رقم أولي
- العدد الأولي هو رقم عد أكبر من 1 ومعامله الوحيدة هي 1 والرقم نفسه.
- تبسيط التعبير
- إن تبسيط التعبير يعني القيام بكل العمليات الحسابية الممكنة.
- اصطلاح
- المصطلح هو ثابت، أو نتاج ثابت ومتغير واحد أو أكثر.
- متغير
- المتغير هو حرف يمثل رقمًا قد تتغير قيمته.


