9.3: כוחות ואן דר ואלס בין אטומים

מבוא

משוואת הגז המושלמת של המצב \(PV=NkT\) אינה מסוגלת לתאר גזים בפועל בטמפרטורות נמוכות, מכיוון שהם עוברים שינוי נפח בלתי רציף והופכים לנוזלים. בשנות ה -70 של המאה ה -19 הגיע הפיזיקאי ההולנדי ואן דר ואלס לשיפור: חוק גז שהכיר במולקולות שקיימו אינטראקציה זו עם זו. הוא הכניס שני פרמטרים כדי לחקות את האינטראקציה הזו. הראשון, כוח בין-מולקולרי אטרקטיבי למרחקים ארוכים, עוזר למשוך את הגז יחד ולכן מפחית את הלחץ החיצוני הדרוש כדי להכיל את הגז בנפח נתון - הגז מעט דק יותר ליד הקירות. הכוח האטרקטיבי לטווח הארוך יכול להיות מיוצג \(-aN/V\) על ידי פוטנציאל שלילי בהתרחקות מהקירות - המולקולות ליד הקירות נמשכות פנימה, אלה בתפזורת נמשכות באופן שווה לכל הכיוונים, כך שבעצם המשיכה לטווח הארוך שווה ערך לפוטנציאל. באר המשתרעת לאורך כל הנפח ומסתיימת קרוב לקירות. כתוצאה מכך, צפיפות הגז \(N/V\) ליד הקירות יורדת בגורם\(e^{-E/kT}=e^{-aN/VkT}\cong 1-aN/VkT\). לכן, הלחץ הנמדד בקיר המכיל הוא מגז מדולל מעט, כך \(P=(N/V)kT\) הופך\(P=(N/V)(1-aN/VkT)kT\), או\((P+a(N/V)^2)V=NkT\). הפרמטר השני שהוסיף ואן דר ואלס היה לקחת בחשבון את הנפח המולקולרי הסופי. לא ניתן לדחוס גז אמיתי ללא הגבלת זמן - הוא הופך לנוזל, לכל המטרות המעשיות שאינו ניתן לדחיסה. הוא ייצג זאת על ידי \(V\) החלפת הנפח ב-\(V-Nb\), \(Nb\) מכונה "הנפח הלא נכלל", בערך נפח המולקולות. הצבת שני המונחים הללו נותנת את המשוואה המפורסמת שלו \[ \left[ P+a\left(\frac{N}{V}\right)^2\right] (V-Nb)=NkT. \label{9.3.1}\]

קירוב גס למדי זה אכן נותן קבוצות של איזותרמות המייצגות את הפיזיקה הבסיסית של מעבר פאזה די טוב. (לפרטים נוספים ודיון מאיר עיניים, ראו למשל נספח ד' לפיזיקה תרמית, מאת ר 'באיירליין.)

אטומי מימן של מצב הקרקע

העניין שלנו כאן הוא בהבנת כוח המשיכה לטווח הארוך של ואן דר ואלס בין אטומים ניטרליים חשמלית למולקולות במונחים מכניים קוונטיים. נתחיל בדוגמה הפשוטה ביותר האפשרית, שני אטומי מימן, שניהם במצב הקרקע:

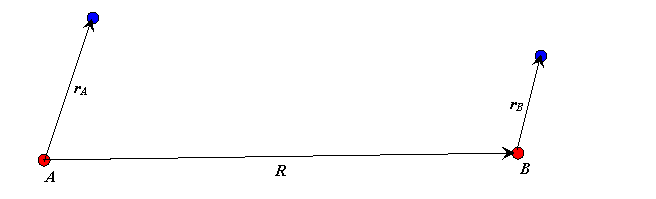
אנו מתייגים את האטומים\(B\), \(A\) והווקטורים מהפרוטונים למיקום האלקטרונים מסומנים על ידי \(\vec{r_A}\) \(\vec{r_B}\) ובהתאמה, \(\vec{R}\) והוא הווקטור מפרוטון \(A\) לפרוטון\(B\).

ואז המילטוניאן\(H=H^0+V\), איפה \[ H^0=-\frac{\hbar^2}{2m}(\nabla^2_A+\nabla^2_B)-\frac{e^2}{r_A}-\frac{e^2}{r_B} \label{9.3.2}\]

והאינטראקציה האלקטרוסטטית בין שני האטומים \[ V=\frac{e^2}{R}+\frac{e^2}{|\vec{R}+\vec{r_B}-\vec{r_A}|}-\frac{e^2}{|\vec{R}+\vec{r_B}|}-\frac{e^2}{|\vec{R}-\vec{r_A}|} \label{9.3.3}\]

מצב הקרקע של \(H^0\) הוא רק תוצר של מצבי הקרקע של האטומים\(A,B\), כלומר, \[ |0\rangle =|100\rangle_A\otimes |100\rangle_B. \label{9.3.4}\]

בהנחה שכעת המרחק בין שני האטומים גדול בהרבה מגודלם, נוכל להרחיב את האינטראקציה \(V\) בפרמטרים הקטנים\(r_A/R,\;  r_B/R\). כפי שניתן לחשוד מהתרשים לעיל, מונחי הסדר המובילים באנרגיה האלקטרוסטטית הם רק אלה של אינטראקציה דיפול-דיפול: \[ V=-e^2(\vec{r_A}\cdot \vec{\nabla})(\vec{r_B}\cdot \vec{\nabla})\frac{1}{R}=e^2\left[ \frac{\vec{r_A}\cdot \vec{r_B}}{R^3}-\frac{3(\vec{r_A}\cdot \vec{R})(\vec{r_B}\cdot \vec{R})}{R^5}\right] \label{9.3.5}\]

אם לוקחים כעת את ציר ה- z לכיוון\(\vec{R}\), אנרגיית האינטראקציה הזו היא \[ V=\frac{e^2}{R^3}(x_Ax_B+y_Ay_B-2z_AZ_B) \label{9.3.6}\]

כעת התיקון מסדר ראשון לאנרגיית מצב הקרקע של מערכת שני האטומים מאינטראקציה זו הוא\(E^1_n=\langle n^0|H^1|n^0\rangle\), היכן כאן \(H^1=V\) ו. \(|n^0\rangle =|100\rangle_A\otimes |100\rangle_B\) החל מהקדנציה הראשונה \(x_Ax_B\) ב \(V\) \[ (_A\langle 100|\otimes_B\langle 100|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle 100|x_A|100\rangle_A)(_B\langle 100|x_B|100\rangle_B) \label{9.3.7}\]

הוא בבירור אפס מכיוון שמצבי הקרקע הם סימטריים כדורית. באופן דומה, המונחים האחרים \(V\) הם אפס לסדר ראשון.

נזכיר כי תיקון האנרגיה מסדר שני הוא\(E^2_n=\sum_{m\neq n} \frac{|\langle m0|H^1|n^0\rangle |^2}{E^0_n-E^0_m} \).

כלומר, \[ E^{(2)}=\sum_{\begin{matrix}n,l,m\\ n′,l′,m′ \end{matrix}} \frac{|(_A\langle nlm|\otimes_B\langle n′l′m′|)V(|100\rangle_A\otimes |100\rangle_B)|^2}{2E_1-E_n-E_{n′}}. \label{9.3.8}\]

מונח טיפוסי כאן הוא \[ (_A\langle nlm|\otimes_B\langle n′l′m′|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle nlm|x_A|100\rangle_A)(_B\langle n′l′m′|x_B|100\rangle_B), \label{9.3.9}\]

אז יסודות המטריצה החד-אטומית הם בדיוק אלה שדיברנו עליהם עבור אפקט סטארק (כפי שהיינו מצפים - זוהי אינטראקציה אלקטרוסטטית!). כמו קודם, רק \(l=1,\;\;  l′=1\) לתרום. כדי לבצע הערכה גסה של הגודל של\(E^{(2)}\), נוכל להשתמש באותו טריק המשמש לאפקט סטארק הריבועי: החלף את המכנים בקבוע \(2E_1\) (המונחים האחרים קטנים בהרבה עבור המצבים המאוגדים, ולמצבי רצף יש מונחי חפיפה קטנים ב המונה). לאחר מכן \(n,l,m,n′,l′,m′\) ניתן לקחת את הסכום על מדינות ביניים כבלתי מוגבל לחלוטין, כולל אפילו מצב הקרקע, נותן \[ \sum_{\begin{matrix}n,l,m\\ n′,l′,m′ \end{matrix}} (|nlm\rangle_A\otimes |n′l′m′\rangle_B)(_A\langle nlm|\otimes_B\langle n′l′m′|)=I, \label{9.3.10}\]

מפעיל הזהות. בקירוב זה, אם כן, בדיוק כמו לאפקט סטארק, \[ E^{(2)}\simeq \frac{e^4}{R^6}\frac{1}{2E_1}(_A\langle 100|\otimes_B\langle 100|)(x_Ax_B+y_Ay_B-2z_AZ_B)^2(|100\rangle_A\otimes |100\rangle_B) \label{9.3.11}\]

\(E_1=-1\)איפה ריד, אז זה הוא הורדת אנרגיה.

בהכפלה\((x_Ax_B+y_Ay_B-2z_AZ_B)^2\), למונחי הצלב יהיו ערכי ציפייה של אפס. פונקציית גל מצב הקרקע היא סימטרית, ולכן כל מה שאנחנו צריכים הוא\(\langle 100|x^2|100\rangle =a^2_0\), איפה \(a_0\) רדיוס בוהר.

זה נותן

\[ E^{(2)}\simeq \frac{e^4}{R^6}\frac{1}{2E_1}6a^4_0\simeq -6\frac{e^2}{R}\left( \frac{a_0}{R}\right)^5 \label{9.3.12}\]

באמצעות\(E_1=-e^2/2a_0\). זכור כי זהו קירוב, אבל אחד די טוב - חישוב מדויק יותר מחליף את 6 על ידי 6.5.

כוחות בין אטום מימן של 1 שניות לאטום מימן של 2 p

עם אטום אחד \(|100\rangle\) והשני ב\(|210\rangle\), למשל, מונח סדר מוביל טיפוסי יהיה

\[ (_A\langle 100|\otimes_B\langle 210|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle 100|x_A|100\rangle_A)(_B\langle 210|x_B|100\rangle_B), \label{9.3.13}\]

וזה בהחלט אפס, כמו כל שאר המונחים המובילים. Baym (הרצאות על מכניקת קוונטים) הסיק מכך כי אין תיקון אנרגיה מסדר מוביל בין שני אטומי מימן אם אחד מהם נמצא במצב הקרקע. זה לא נכון: המצב הנרגש הראשון של מערכת שני האטומים (ללא אינטראקציה) מנוון, ולכן, בדיוק כמו למתנד ההרמוני הפשוט הדו-ממדי שטופל בהרצאה הקודמת, עלינו לאלכסן את ההפרעה בתת-מרחב של מצבים נרגשים ראשונים מנוונים אלה. (עבור חלק זה, אנו עוקבים מקרוב אחר הטיפול המצוין במכניקת הקוונטים, מאת סי כהן-טאנודג'י ואח '.)

המרחב של המצבים הנרגשים הראשונים המנוונים של שני האטומים הלא אינטראקטיביים משתרע על ידי מחבטי מרחב המוצר: \[ \begin{matrix} (|100\rangle_A\otimes |200\rangle_B), &(|200\rangle_A\otimes |100\rangle_B),&(|100\rangle_A\otimes |211\rangle_B),&(|211\rangle_A\otimes |100\rangle_B),\\ (|100\rangle_A\otimes |210\rangle_B),&(|210\rangle_A\otimes |100\rangle_B),&(|100\rangle_A\otimes |21-1\rangle_B),&(|21-1\rangle_A\otimes |100\rangle_B). \end{matrix} \label{9.3.14}\]

המשימה, אם כן, היא להתלכסן \(V=\frac{e^2}{R^3}(x_Ax_B+y_Ay_B-2z_AZ_B)\) בתת-חלל שמונה ממדי זה.

אנו מתחילים בייצוג \(V\) \(8\times 8\) כמטריצה תוך שימוש במצבים אלה כבסיס. ראשית, שים לב שכל האלמנטים האלכסוניים של המטריצה הם אפסים - בכולם אנו מוצאים את הממוצע של x, y או z עבור אחד האטומים במצב הקרקע. שנית, כתיבה\(V=\frac{e^2}{R^3}(\vec{r_A}\cdot \vec{r_B}-3z_AZ_B)\), ניכר כי \(V\) הוא ללא שינוי אם המערכת מסובבת סביב ציר z (הקו המצטרף לשני הפרוטונים). המשמעות היא שלקומוטטור\([V,L_z]=0\), היכן \(L_z\) נמצא רכיב המומנטום הזוויתי הכולל בכיוון z, כך \(V\) שיהיו רק אלמנטים מטריצה שאינם אפסיים בין מצבים בעלי אותו סך הכל. \(L_z\) שלישית, מהזוגיות (או Wigner-Eckart) כל רכיבי המטריצה בתת-חלל המשתרעים על ידי חייבים להיות אפס. \((|100\rangle_A\otimes |200\rangle_B),\; (|200\rangle_A\otimes |100\rangle_B)\)

זה מקטין את החלק nonzero של \(8\times 8\) המטריצה לתוצר ישיר של שלוש \(2\times 2\) מטריצות, המתאים לשלושת הערכים של. \(L_z=m\) לדוגמה, \(m=0\) תת-החלל משתרע על ידי. \((|100\rangle_A\otimes |210\rangle_B),\; (|210\rangle_A\otimes |100\rangle_B)\) האלמנטים האלכסוניים של \(2\times 2\) המטריצה הם אפס, האלמנטים האלכסוניים שווים ל\(-2\frac{e^2}{R^3}(_A\langle 100|z_A|210\rangle_A)(_B\langle 210|Z_B|100\rangle_B)\), שם שמרנו על התוויות המיותרות \(A,B\) כדי להבהיר מהיכן מגיע המונח הזה. (\(y_A\)התנאים \(x_A\) והתנאים לא יתרמו\(m=0\).)

זהו כעת אינטגרל פשוט על פני פונקציות גלי מימן. לשלוש \(2\times 2\) המטריצות יש את הצורה \[ \begin{pmatrix} 0&k_m/R^3\\ k_m/R^3 &0 \end{pmatrix} \label{9.3.15}\]

(בעקבות הסימון של כהן-טאנודג'י) היכן, והערכים העצמיים האנרגטיים נמצאים\(k_m\sim e^2a^2_0\), עם סמלים עצמיים תואמים. \(\pm k_m/R^3\) \( (1/\sqrt{2})[(|100\rangle_A\otimes |210\rangle_B)\pm (|210\rangle_A\otimes |100\rangle_B)]\)

אז עבור שני אטומי מימן, אחד במצב הקרקע ואחד במצב הנרגש הראשון, אנרגיית האינטראקציה של ואן דר וואל חשובה הרבה יותר \(1/R^6\) מהאנרגיה לשני אטומי מימן במצב הקרקע. \(1/R^3\) שימו לב גם שה \(1/R^3\) יכול להיות חיובי או שלילי, תלוי אם האטומים נמצאים במצב שווה או מוזר - כך שהאטומים לפעמים דוחים זה את זה.

לבסוף, אם שני אטומים נמצאים בתחילה במצב\((|100\rangle_A\otimes |210\rangle_B)\), שים לב שזה לא מצב עצמי של המילטוניאן כאשר האינטראקציה כלולה. כתיבת המצב כסכום של המצבים הזוגיים והמוזרים, שיש להם תדרי פאזה שונים במקצת מהפרש האנרגיה, אנו מוצאים שהעירור נע קדימה ואחורה בין שני האטומים עם נקודה\(hR^3/2k_{m=0}\).