2.2: אלגברה לינארית

מבוא

ראינו שבמכניקת הקוונטים, מצב האלקטרון בפוטנציאל כלשהו ניתן על ידי פונקציית גל\(\psi(\vec x,t)\), ומשתנים פיזיקליים מיוצגים על ידי אופרטורים בפונקציית גל זו, כגון המומנטום בכיוון \(p_x =-i\hbar\partial/\partial x\)x. משוואת הגל שרדינגר היא משוואה ליניארית, כלומר אם \(\psi_1\) \(\psi_2\) הם פתרונות, אז כך הוא\(c_1\psi_1+c_2\psi_2\), איפה מספרים \(c_1, c_2\) מרוכבים שרירותיים.

ליניאריות זו של קבוצות הפתרונות האפשריים נכונה בדרך כלל במכניקת הקוונטים, וכך גם ייצוג המשתנים הפיזיים על ידי אופרטורים בפונקציות הגל. המבנה המתמטי שמתאר זאת, הסט הליניארי של מצבים אפשריים וקבוצות אופרטורים במצבים אלה, הוא למעשה אלגברה לינארית של אופרטורים הפועלים על מרחב וקטורי. מעתה והלאה, זו השפה בה נשתמש רוב הזמן. כדי להבהיר, אנו נותנים כמה הגדרות.

מהו מרחב וקטורי?

המרחב הווקטורי האב טיפוסי הוא כמובן קבוצת הווקטורים האמיתיים במרחב תלת מימדי רגיל, וקטורים אלה יכולים להיות מיוצגים על ידי שלישיות של מספרים אמיתיים \((v_1,v_2,v_3)\) המודדים את הרכיבים בכיווני x, y ו - z בהתאמה.

המאפיינים הבסיסיים של וקטורים אלה הם:

• כל וקטור מוכפל במספר הוא וקטור אחר במרחב,\(a(v_1,v_2,v_3)=(av_1,av_2,av_3)\);
• הסכום של שני וקטורים הוא וקטור נוסף במרחב, שניתן רק על ידי הוספת הרכיבים המתאימים יחד:\((v_1+w_1,v_2+w_2,v_3+w_3)\).

שני המאפיינים הללו יחד מכונים "סגירה": הוספת וקטורים והכפלתם במספרים לא יכולה להוציא אותך מהחלל.

• מאפיין נוסף הוא שיש וקטור null ייחודי \((0,0,0)\) ולכל וקטור יש היפוך תוסף \((-v_1,-v_2,-v_3)\) שנוסף לווקטור המקורי נותן את וקטור האפס.

מתמטיקאים הכללו את ההגדרה של מרחב וקטורי: למרחב וקטורי כללי יש את המאפיינים שרשמנו לעיל עבור וקטורים אמיתיים תלת מימדיים, אך פעולות ההוספה והכפל במספר מוכללות לפעולות מופשטות יותר בין ישויות כלליות יותר. עם זאת, המפעילים מוגבלים להיות קומוטטיביים ואסוציאטיביים.

שימו לב שרשימת המאפיינים הדרושים למרחב וקטורי כללי אינה כוללת שלווקטורים יש גודל - זו תהיה דרישה נוספת, ותיתן מה שנקרא מרחב וקטורי נורמלי. עוד על כך בהמשך.

כדי לעבור מהמרחב הווקטורי התלת מימדי המוכר למרחבים הווקטוריים הרלוונטיים למכניקת הקוונטים, ראשית יש להכליל את המספרים האמיתיים (מרכיבי הווקטור וגורמים מתרבים אפשריים) למספרים מרוכבים, ושנית הווקטור התלת-רכיבי עובר וקטור רכיב n. המרחב המורכב n -ממדי כתוצאה מכך מספיק כדי לתאר את מכניקת הקוונטים של המומנטום הזוויתי, נושא חשוב. אבל כדי לתאר את פונקציית הגל של חלקיק בקופסה נדרש מרחב ממדי אינסופי, ממד אחד לכל רכיב פורייה, וכדי לתאר את פונקציית הגל של חלקיק בקו אינסופי נדרש מערך של כל הפונקציות הניתנות להפרדה רציפה מנורמלת בקו זה. למרבה המזל, כל ההכללות הללו הן לקבוצות סופיות או אינסופיות של מספרים מרוכבים, כך שדרישות המרחב הווקטורי של המתמטיקאים לגבי קומוטטיביות ואסוציאטיביות תמיד מרוצות באופן טריוויאלי.

אנו משתמשים בסימון של דיראק עבור וקטורים, \(|1\rangle,|2\rangle\) וקוראים להם "kets", כך, בשפתו, אם \(|1\rangle,|2\rangle\) שייכים למרחב, כך גם \(c_1|1\rangle +c_2|2\rangle\) עבור קבועים מורכבים שרירותיים. \(c_1, c_2\) מכיוון שהווקטורים שלנו מורכבים ממספרים מרוכבים, הכפלת כל וקטור באפס נותנת את וקטור האפס, וההיפוך התוסף ניתן על ידי היפוך הסימנים של כל המספרים בווקטור.

ברור שמערך הפתרונות של משוואת שרדינגר לאלקטרון בפוטנציאל עונה על הדרישות למרחב וקטורי: \(\psi(\vec x,t)\) הוא רק מספר מרוכב בכל נקודה במרחב, כך שרק מספרים מרוכבים מעורבים ביצירה, וקומוטטיביות\(c_1\psi_1+c_2\psi_2\), אסוציאטיביות וכו ', עקבו בבת אחת.

ממדיות מרחב וקטורי

הווקטורים עצמאיים \( |1\rangle ,|2\rangle ,|3\rangle\) באופן ליניארי אם \[ c_1|1\rangle +c_2|2\rangle +c_3|3\rangle =0 \tag{2.2.1}\]

מרמז \[ c_1=c_2=c_3=0 \tag{2.2.2}\]

מרחב וקטורי הוא n-ממדי אם המספר המרבי של וקטורים עצמאיים ליניארית במרחב הוא n.

מרחב כזה נקרא לעתים קרובות\(V^n(C)\), או \(V^n(R)\) אם רק מספרים ממשיים משמשים.

כעת, מרחבים וקטוריים עם ממד סופי n אינם מספיקים בבירור לתיאור פונקציות של משתנה רציף איקס. אבל כדאי מאוד לעיין בהם כאן: כפי שהזכרנו, הם מתאימים לתיאור המומנטום הזוויתי הכמותי, והם משמשים מבוא טבעי למרחבים האינסופיים הממדיים הדרושים לתיאור פונקציות גל מרחביות.

קבוצה של נ וקטורים עצמאיים ליניארית במרחב n -ממדי הוא בסיס - ניתן לכתוב כל וקטור בצורה ייחודית כסכום על בסיס: \[ |V\rangle=\sum v_i|i\rangle \tag{2.2.3}\]

אתה יכול לבדוק את הייחודיות על ידי לקיחת ההבדל בין שני סכומים נפרדים כביכול: זה יהיה קשר ליניארי בין וקטורים עצמאיים, סתירה.

מכיוון שניתן לכתוב את כל הווקטורים במרחב כסכומים ליניאריים על יסודות הבסיס, לסכום הכפולות של כל שני וקטורים יש את הצורה: \[ a|V\rangle+b|W\rangle=\sum (av_i+bw_i)|i\rangle \tag{2.2.4}\]

חללי מוצר פנימיים

למרחבים הווקטוריים הרלוונטיים במכניקת הקוונטים יש גם פעולה המקשרת מספר לזוג וקטורים, הכללה של תוצר הנקודה של שני וקטורים תלת מימדיים רגילים, \[ \vec a, \vec b =\sum a_ib_i \tag{2.2.5}\]

בעקבות דיראק, אנו כותבים את התוצר הפנימי של שני וקטורי \(|V\rangle,|W\rangle\) ket כ. \(\langle W|V\rangle\) דיראק מתייחס \(\langle \; | \; \rangle\) לצורה זו כ"סוגר "המורכב מ"חזייה" ו"קט". המשמעות היא שלכל וקטור ket \(|V\rangle\) יש חזייה קשורה\(\langle V|\). במקרה של וקטור n ממדי אמיתי, \(|V\rangle,\langle V|\) הם זהים - אך אנו דורשים למקרה הכללי יותר \[ \langle W|V\rangle=\langle V|W\rangle^*\tag{2.2.6}\]

איפה \(*\) מציין מצומד מורכב. זה מרמז כי עבור ket \((v_1,...,v_n)\) החזייה תהיה\((v_1^*,...,v_n^*)\). (למעשה, חזיות נכתבות בדרך כלל כשורות, כעמודות כעמודות, כך שהתוצר הפנימי עוקב אחר הכללים הסטנדרטיים להכפלת מטריצות.) ככל הנראה עבור הווקטור המורכב הממדי n \(\langle V|V\rangle\) הוא אמיתי וחיובי למעט וקטור האפס:

\[ \langle V|V\rangle=\sum_1^n |v_i|^2 \tag{2.2.7}\]

עבור מרחבי המוצר הפנימיים הכלליים יותר הנחשבים מאוחר יותר אנו דורשים \(\langle V|V\rangle\) להיות חיוביים, למעט וקטור האפס. (דרישות אלה אכן מגבילות את מחלקות המרחבים הווקטוריים שאנו שוקלים - ללא מדד לורנץ, למשל - אך כולם מרוצים מהמרחבים הרלוונטיים למכניקת הקוונטים הלא רלטיביסטית.)

הנורמה של \(|V\rangle\) מוגדרת אז על ידי \[ |V|=\sqrt{\langle V|V\rangle} \tag{2.2.8}\]

אם \(|V\rangle\) הוא חבר ב\(V^n(C)\), כך הוא\(a|V\rangle\), עבור כל מספר מורכב\(a\).

אנו דורשים את פעולת המוצר הפנימי לנסוע עם כפל במספר, כך

\[ \langle W|(a|V\rangle)=a\langle W|V\rangle \tag{2.2.9}\]

המצומד המורכב של הצד הימני הוא\(a^*\langle V|W\rangle\). לצורך עקביות, החזייה המתאימה לקט \(a|V\rangle\) חייבת להיות \(\langle V|a^*\) - בכל מקרה ברורה מהגדרת החזייה במידות מורכבות n שניתנו לעיל.

מכאן נובע שאם \[ |V\rangle=\sum v_i|i\rangle, \; |W\rangle=\sum w_i|i\rangle, \; then \; \langle V|W\rangle=\sum v_i^*w_j \langle i|j\rangle \tag{2.2.10}\]

בניית בסיס אורתונורמלי: תהליך גראם-שמידט

כדי שיהיה משהו שדומה יותר למוצר הנקודה הסטנדרטי של שלושה וקטורים רגילים\(\langle i|j\rangle=\delta_{ij}\), אנחנו צריכים, כלומר, אנחנו צריכים לבנות בסיס אורתונורמלי בחלל. יש הליך פשוט לעשות זאת שנקרא תהליך גראם-שמידט. אנו מתחילים עם קבוצה עצמאית ליניארית של וקטורי בסיס,\(|1\rangle, |2\rangle, |3\rangle\),....

תחילה אנו מנרמלים \(|1\rangle\) על ידי חלוקתו לפי הנורמה שלה. התקשר לווקטור המנורמל\(|I\rangle\). עכשיו \(|2\rangle\) לא יכול להיות מקביל ל\(|I\rangle\), כי הבסיס המקורי היה של וקטורים עצמאיים ליניארית, אבל \(|2\rangle\) באופן כללי יש רכיב nonzero מקביל\(|I\rangle\), שווה ל\(|I\rangle\langle I|2\rangle\), מאז \(|I\rangle\) הוא מנורמל. לכן, הווקטור \(|2\rangle-|I\rangle\langle I|2\rangle\) מאונך\(|I\rangle\), כפי שניתן לאמת בקלות. זה גם קל לחשב את הנורמה של וקטור זה, ולחלק על ידי זה כדי לקבל\(|II\rangle\), החבר השני של בסיס אורתונורמלי. בשלב הבא אנו מורידים \(|3\rangle\) ומחסירים את מרכיביו בכיוונים\(|II\rangle\), \(|I\rangle\) ומנרמלים את השאר וכן הלאה.

במרחב n ממדי, לאחר שבנה בסיס אורתונורמלי עם חברים\(|i\rangle\), \(|V\rangle\) ניתן לכתוב כל וקטור כווקטור עמודה, \[ |V\rangle= \sum v_i |i\rangle= \begin{pmatrix}v_1 \\ v_2 \\ . \\ . \\ v_n \end{pmatrix} \, , \; where \; |1\rangle= \begin{pmatrix}1 \\ 0 \\ . \\ . \\ 0 \end{pmatrix} \; and \: so \: on. \tag{2.2.11}\]

החזייה המתאימה היא\(\langle V|=\sum v_i^*\langle i|\), אותה אנו כותבים כווקטור שורה עם האלמנטים מורכבים מצומדים,\(\langle V|=(v_1^*,v_2^*,...v_n^*)\). פעולה זו, העוברת מעמודות לשורות ולוקחת את המצומד המורכב, נקראת לקיחת הצמוד, וניתן להחיל אותה גם על מטריצות, כפי שנראה בקרוב.

הסיבה לייצוג החזייה כשורה היא שהתוצר הפנימי של שני וקטורים ניתן אז על ידי כפל מטריקס סטנדרטי: \[ \langle V|W\rangle=(v_1^*,v_2^*,...,v_n^*) \begin{pmatrix}w_1\\ . \\ . \\ w_n \end{pmatrix} \tag{2.2.12}\]

(כמובן שזה עובד רק עם בסיס אורתונורמלי.)

אי השוויון של שוורץ

אי השוויון בשוורץ הוא הכללה לכל מרחב תוצר פנימי של התוצאה \(|\vec a ,\vec b|^2 \le |\vec a|^2|\vec b|^2\) (או\(\cos^2 \theta \le1\)) עבור וקטורים תלת מימדיים רגילים. סימן השוויון בתוצאה זו מתקיים רק כאשר הווקטורים מקבילים. כדי להכליל לממדים גבוהים יותר, אפשר רק לציין ששני וקטורים נמצאים בתת-מרחב דו מימדי, אך דרך מאירה להבנת אי השוויון היא לכתוב את הווקטור \(\vec a\) כסכום של שני מרכיבים, אחד מקביל ואחד בניצב ל\(\vec b\). \(\vec b\) הרכיב המקביל אליו \(\vec b\) הוא צודק\(\vec b(\vec a\cdot \vec b)/|\vec b|^2\), כך שהרכיב הניצב אליו \(\vec b\) הוא הווקטור\(\vec a_{\bot}=\vec a-\vec b(\vec a\cdot\vec b)/|\vec b|^2 \). החלפת הביטוי הזה\(\vec a_{\bot}\cdot\vec a_{\bot} \ge0 \), אי השוויון בא בעקבותיו.

אותה נקודה יכולה להיעשות במרחב מוצר פנימי כללי: אם\(|V\rangle\), \(|W\rangle\) הם שני וקטורים, אז \[ |Z\rangle=|V\rangle-\frac{|W\rangle \langle W|V\rangle}{|W|^2} \tag{2.2.13}\]

הוא המרכיב של \(|V\rangle\) בניצב\(|W\rangle\), כפי שנבדק בקלות על ידי לקיחת המוצר הפנימי שלו עם\(|W\rangle\).

ואז \[ \langle Z|Z\rangle \ge0 \;\; gives\; immediately\;\; |\langle V|W\rangle|^2 \le |V|^2|W|^2 \tag{2.2.14}\]

אופרטורים לינאריים

אופרטור ליניארי A לוקח כל וקטור במרחב וקטורי ליניארי לווקטור במרחב זה, \(A|V\rangle=|V'\rangle\) ומספק \[A(c_1|V_1\rangle+c_2|V_2\rangle)= c_1A|V_1\rangle+c_2A|V_2\rangle \tag{2.2.15}\]

עם\(c_1\), קבועים מורכבים \(c_2\) שרירותיים.

מפעיל הזהות \(I\) הוא (ברור!) מוגדר על ידי: \[ I|V\rangle=|V\rangle \;\; for \; all \; |V\rangle \tag{2.2.16}\]

עבור מרחב וקטורי ממדי n עם בסיס אורתונורמלי\(|1\rangle,...,|n\rangle\), מכיוון שכל וקטור במרחב יכול לבוא לידי ביטוי כסכום\(|V\rangle=\sum v_i|i\rangle\), האופרטור הליניארי נקבע לחלוטין על ידי פעולתו על וקטורי הבסיס - זה כל מה שאנחנו צריכים לדעת. קל למצוא ביטוי למפעיל הזהות מבחינת חזיות וקטים.

נטילת המוצר הפנימי של שני צידי המשוואה \(|V\rangle=\sum v_i|i\rangle\) עם החזייה \(\langle i|\) נותנת\(\langle i|V\rangle=v_i\), כך \[ |V\rangle=\sum v_i|i\rangle=\sum |i\rangle\langle i|V\rangle \tag{2.2.17}\]

מכיוון שזה נכון לגבי כל וקטור במרחב, מכאן נובע שמפעיל הזהות הוא פשוט \[ I=\sum_1^n |i\rangle\langle i| \tag{2.2.18}\]

זוהי תוצאה חשובה: היא תופיע שוב בתחפושות רבות.

כדי לנתח את הפעולה של מפעיל ליניארי כללי\(A\), אנחנו רק צריכים לדעת איך זה פועל על כל וקטור בסיס. ראשית\(A|1\rangle\), זה חייב להיות סכום כלשהו על וקטורי הבסיס, ומכיוון שהם אורתונורמליים, הרכיב \(|i\rangle\) בכיוון חייב להיות צודק. \(\langle i|A|1\rangle\)

כלומר, \[ A|1\rangle=\sum_1^n |i\rangle\langle i|A|1\rangle=\sum_1^n A_{i1}|i\rangle\, ,\; writing\; \langle i|A|1\rangle =A_{i1} \tag{2.2.19}\]

אז אם האופרטור הליניארי A הפועל על \(|V\rangle=\sum v_i|i\rangle\) נותן\(|V'\rangle=\sum v_i'|i\rangle\), כלומר\(A|V\rangle=|V'\rangle\), הליניאריות אומרת לנו את זה \[ \sum v_i'|i\rangle=|V'\rangle=A|V\rangle=\sum v_j A|j\rangle= \sum_{i,j} v_j |i\rangle\langle i|A|j\rangle=\sum_{i,j} v_j A_{ij}|i\rangle \tag{2.2.20}\]

שם בשלב הרביעי פשוט הכנסנו את מפעיל הזהות.

מכיוון שה- s \(|i\rangle\) כולם אורתוגונליים, המקדם של מסוים \(|i\rangle\) בצד שמאל של המשוואה חייב להיות זהה למקדם של אותו \(|i\rangle\) בצד ימין. כלומר,\(v_i'=A_{ij}v_j\).

לכן המפעיל פשוט \(A\) שווה ערך לכפל מטריקס:

\[\begin{pmatrix}v_1'\\ v_2'\\ .\\ .\\ v_n'\end{pmatrix}= \begin{pmatrix} \langle1|A|1\rangle &\langle1|A|2\rangle & .& .&\langle1|A|n\rangle\\ \langle2|A|1\rangle &\langle2|A|2\rangle & .& .& .\\ .& .& .& .& .\\ . & .& .& .& .\\ \langle n|A|1\rangle &\langle n|A|2\rangle & .& .&\langle n|A|n\rangle \end{pmatrix} \begin{pmatrix}v_1\\ v_2\\ .\\ .\\ v_n\end{pmatrix} \tag{2.2.21}\]

ככל הנראה, אם כן, החלת שני אופרטורים ליניאריים בזה אחר זה שקולה להכפלת מטריצות רצופה - ולכן, מכיוון שמטריצות אינן נוסעות באופן כללי, וגם לא אופרטורים ליניאריים. (כמובן שאם אנו מקווים לייצג משתנים קוונטיים כאופרטורים ליניאריים במרחב וקטורי, זה חייב להיות נכון - מפעיל המומנטום \(p=-i\hbar d/dx\) בהחלט לא נוסע עם x!)

מפעילי הקרנה

חשוב לציין כי אופרטור ליניארי המיושם ברצף על חברי בסיס אורתונורמלי עשוי לתת קבוצה חדשה של וקטורים שכבר אינם משתרעים על כל החלל. כדי לתת דוגמה, האופרטור הליניארי \(|1\rangle\langle 1|\) המוחל על כל וקטור במרחב בוחר את רכיב הווקטור \(|1\rangle\) בכיוון. זה נקרא מפעיל הקרנה. המפעיל \((|1\rangle\langle 1|+|2\rangle\langle 2|)\) מקרין וקטור למרכיביו בתת-חלל המשתרע על ידי הווקטורים \(|1\rangle\) וכן \(|2\rangle\) הלאה - אם נרחיב את הסכום כך שיהיה על כל הבסיס, אנו משחזרים את אופרטור הזהות.

תרגיל: להוכיח כי ייצוג המטריצה של מפעיל ההקרנה \((|1\rangle\langle 1|+|2\rangle\langle 2|)\) כולל את כל האלמנטים אפס למעט שני האלמנטים האלכסוניים הראשונים, השווים לאחד.

לא יכול להיות אופרטור הפוך למפעיל הקרנה לא טריוויאלי, מכיוון שהמידע על רכיבי הווקטור הניצב לתת-חלל המוקרן הולך לאיבוד.

המפעיל הצמוד והמטריצות ההרמיטיות

כפי שדיברנו, אם ket \(|V\rangle\) במרחב הממדי n כתוב כווקטור עמודה עם רכיבים \(n\) (מורכבים), החזייה המתאימה היא וקטור שורה שיש כאלמנטים את המצמידים המורכבים של אלמנטים ket. \(\langle W|V\rangle=\langle V|W\rangle^*\)לאחר מכן עוקב באופן אוטומטי מכללי כפל מטריצות סטנדרטיים, ועל \(|V\rangle\) הכפלת מספר מרוכב \(a\) כדי לקבל \(a|V\rangle\) (כלומר כל אלמנט בעמודת המספרים מוכפל\(a\)) החזייה המתאימה עוברת אליו\(\langle V|a^*=a^*\langle V|\).

אבל נניח שבמקום להכפיל ket במספר, אנחנו פועלים על זה עם מפעיל ליניארי. מה מייצר את השינוי המקביל בין החזיות? במילים אחרות, אם\(A|V\rangle=|V'\rangle\), לאיזה מפעיל שולח \(\langle V|\) את החזייה\(\langle V'|\)? זה חייב להיות מפעיל ליניארי, כי \(A\) הוא ליניארי, כלומר, אם תחת \(A\) \(|V_1\rangle \to |V_1'\rangle\)\(|V_3\rangle=|V_1\rangle +|V_2\rangle\), \(|V_2\rangle \to |V_2'\rangle\) ולאחר מכן תחת \(A\) \(|V_3\rangle\) נדרש להגיע\(|V_3'\rangle=|V_1'\rangle +|V_2'\rangle\). כתוצאה מכך, תחת טרנספורמציה החזייה המקבילה עלינו להיות\(\langle V_1|\to \langle V_1'|\), \(\langle V_2|\to \langle V_2'|\) ו\(\langle V_3|\to \langle V_3'|\), - שינוי החזייה הוא בהכרח גם ליניארי. כזכור כי החזייה היא וקטור שורה של אלמנטים n, הטרנספורמציה הליניארית הכללית ביותר השולחת אותה לחזייה אחרת היא \(n\times n\) מטריצה הפועלת על החזייה מימין.

מפעיל חזייה זה נקרא התוספת של\(A\), כתוב\(A^{\dagger}\). כלומר, לקט \(A|V\rangle\) יש חזייה מתאימה\(\langle V|A^{\dagger}\). בבסיס אורתונורמלי, השתמש בסימון לציון החזייה \(\langle i|A^{\dagger}\) המתאימה \(\langle Ai|\) לקט, נניח, \(A|i\rangle=|Ai\rangle\) \[ (A^{\dagger})_{ij}=\langle i|A^{\dagger}|j\rangle=\langle Ai|j\rangle=\langle j|Ai\rangle^*=A_{ji}^* \tag{2.2..22}\]

אז האופרטור הצמוד הוא מצומד מורכב הטרנספוזיציה.

חשוב: עבור מוצר של שני אופרטורים (להוכיח את זה!) , \[ (AB)^{\dagger}=B^{\dagger}A^{\dagger} \tag{2.2..23}\]

מפעיל השווה לצדו \(A=A^{\dagger}\) נקרא הרמיטיאן. כפי שנמצא בהרצאה הבאה, למפעילים הרמיטיים יש חשיבות מרכזית במכניקת הקוונטים. מפעיל השווה למינוס הצמוד שלו,\(A=-A^{\dagger}\), הוא אנטי הרמיטי (המכונה לפעמים הרמיטי מוטה). שני סוגי המפעילים הללו הם בעצם הכללות של מספר אמיתי ודמיוני: כל מפעיל יכול לבוא לידי ביטוי כסכום של מפעיל הרמיטי ומפעיל אנטי הרמיטי, \[ A=\frac{1}{2}(A+A^{\dagger})+\frac{1}{2}(A-A^{\dagger}) \tag{2.2.24}\]

ההגדרה של adjoint משתרעת באופן טבעי על וקטורים ומספרים: הצמוד של ket הוא החזייה המתאימה, הצמוד של מספר הוא המצומד המורכב שלו. זה שימושי לזכור כאשר לוקחים את התוספת של אופרטור אשר עשוי להיות בנוי חלקית של וקטורים ומספרים, כגון אופרטורים מסוג הקרנה. החיבור של תוצר של מטריצות, וקטורים ומספרים הוא תוצר של המפרקים בסדר הפוך. (כמובן, עבור מספרים הסדר לא משנה.)

מפעילים יחידים

מפעיל הוא יחיד אם\(U^{\dagger }U=1\). זה מרמז תחילה כי \(U\) הפעלה על כל וקטור נותנת וקטור בעל אותה נורמה, שכן הנורמה החדשה\(\langle V|U^{\dagger }U|V\rangle=\langle V|V\rangle\). יתר על כן, מוצרים פנימיים נשמרים,\(\langle W|U^{\dagger }U|V\rangle=\langle W|V\rangle\). לכן, תחת טרנספורמציה יחידה הבסיס האורתונורמלי המקורי בחלל חייב לעבור לבסיס אורתונורמלי אחר.

לעומת זאת, כל טרנספורמציה שלוקחת בסיס אורתונורמלי אחד למשנהו היא טרנספורמציה יחידה. כדי לראות זאת, נניח שטרנספורמציה ליניארית \(A\) שולחת את חברי הבסיס \((|1\rangle_1,|2\rangle_1,...,|n\rangle_1)\) האורתונורמלי למערך האורתונורמלי השונה\((|1\rangle_2,|2\rangle_2,...,|n\rangle_2)\), כך וכו 'ואז הווקטור \(|V\rangle= \sum v_i |i\rangle_1\) ילך אליו\(A|1\rangle_1=|1\rangle_2\), בעל אותה נורמה\(|V'\rangle=A|V\rangle=\sum v_i |i\rangle_2\),. \(\langle V'|V'\rangle= \langle V|V\rangle=\sum |v_i|^2\) אלמנט מטריצה\(\langle W'|V'\rangle= \langle W|V\rangle=\sum w_i^*v_i\), אבל גם\(\langle W'|V'\rangle=\langle W|A^{\dagger}A|V\rangle\). כלומר, \(\langle W|V\rangle= \langle W|A^{\dagger}A|V\rangle\) עבור kets שרירותיים\(|V\rangle, \: |W\rangle\). זה אפשרי רק אם\(A^{\dagger}A=1\), כך גם \(A\) יחידתי.

פעולה יחידה מסתכמת בסיבוב (אולי בשילוב עם השתקפות) בחלל. ככל הנראה\(U^{\dagger}U=1\), מכיוון שהג'וינט \(U^{\dagger}\) מסובב את הבסיס לאחור - זו הפעולה ההפוכה, וכך \(UU^{\dagger}=1\) גם, כלומר, ונסיעות. \(U\) \(U^{\dagger}\)

דטרמיננטים

אנו בודקים בסעיף זה את הקובע של מטריצה, פונקציה הקשורה קשר הדוק למאפייני המפעיל של המטריצה.

נתחיל עם \(2\times2\) מטריצות: \[ A=\begin{pmatrix} a_{11} &a_{12} \\ a_{21} &a_{22} \end{pmatrix} \tag{2.2.25}\]

הקובע של מטריצה זו מוגדר על ידי: \[ \det A=|A|=a_{11}a_{22}-a_{12}a_{21} \tag{2.2.26}\]

כתיבת שתי שורות המטריצה כווקטורים: \[ \vec a_1^R=(a_{11},a_{12}) \\ \vec a_2^R=(a_{21},a_{22}) \tag{2.2.27}\]

(\(R\)מציין שורה), \(\det A=\vec a_1^R \times \vec a_2^R\) הוא רק השטח (עם הסימן המתאים) של המקבילית עם שני וקטורי השורה כצדדים סמוכים:

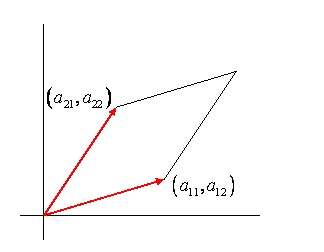
זהו אפס אם שני הווקטורים מקבילים (תלויים ליניארית) ואינם משתנים על ידי הוספת מכפיל כלשהו של \(\vec a_2^R\) to \(\vec a_2^R\) (מכיוון שלמקבילית החדשה יש אותו בסיס וגובה זהה למקור - בדוק זאת על ידי ציור).

בואו נמשיך למקרה המעניין יותר של \(3\times3\) מטריצות: \[ A=\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix} \tag{2.2.28}\]

הקובע של \(A\) מוגדר כ \[ \det A=\varepsilon_{ijk}a_{1i}a_{2j}a_{3k} \tag{2.2.29}\]

כאשר \(\varepsilon_{ijk}=0\) אם שניים שווים, +1 אם \(ijk = 123, \; 231 \; or\; 312\) (כלומר תמורה אחידה של 123) ו -1 אם \(ijk\) היא תמורה מוזרה של 123. סיומות חוזרות ונשנות, כמובן, מרמזות כאן על סיכום.

לכתוב את זה במפורש, \[ \det A= a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{31}a_{12}a_{23}-a_{11}a_{32}a_{23}-a_{21}a_{12}a_{33}-a_{31}a_{22}a_{13} \tag{2.2.30}\]

בדיוק כמו בשני ממדים, כדאי להסתכל על הביטוי הזה במונחים של וקטורים המייצגים את שורות המטריצה \[ \vec a_1^R=(a_{11},a_{12},a_{13}) \\ \vec a_2^R=(a_{21},a_{22},a_{23}) \\ \vec a_3^R=(a_{31},a_{32},a_{33}) \tag{2.2.31}\]

כך \[ A= \begin{pmatrix} \vec a_1^R\\ \vec a_2^R\\ \vec a_3^R \end{pmatrix} \: , \; and \; we \; see \; that \; \det A=(\vec a_1^R \times \vec a_2^R)\cdot \vec a_3^R \tag{2.2.32}\]

זהו נפח המקביל שנוצר על ידי שלושת הווקטורים שהם צדדים סמוכים (נפגשים בפינה אחת, המקור).

נפח מקביל זה יהיה כמובן אפס אם שלושת הווקטורים שוכבים במישור, והוא לא ישתנה אם יתווסף מכפיל של אחד הווקטורים לאחד מהווקטורים. כלומר, הקובע של מטריצה לא משתנה אם מכפיל של שורה אחת מתווסף לשורה אחרת. הסיבה לכך היא שהקובע הוא ליניארי באלמנטים של שורה אחת, \[ \det \begin{pmatrix} \vec a_1^R+\lambda\vec a_2^R \\ \vec a_2^R \\ \vec a_3^R \end{pmatrix}=\det \begin{pmatrix} \vec a_1^R\\ \vec a_2^R \\ \vec a_3^R \end{pmatrix} +\lambda\det \begin{pmatrix} \vec a_2^R\\ \vec a_2^R\\ \vec a_2^R \end{pmatrix} \tag{2.2.33}\]

והמונח האחרון הוא אפס מכיוון ששתי שורות זהות - כך שהתוצר הווקטורי המשולש נעלם.

דרך כללית יותר לקבוע זאת, החלה על דטרמיננטים גדולים יותר, היא שעבור קובע בעל שתי שורות זהות, הסימטריה של שתי השורות, יחד עם האנטי-סימטריה של\(\varepsilon_{ijk}\), מבטיחה שהמונחים בסכום מתבטלים בזוגות.

מכיוון שהקובע אינו משתנה על ידי הוספת מספר מכפיל של שורה אחת לאחרת, אם השורות תלויות באופן ליניארי, ניתן להפוך שורה אחת לאפס זהה על ידי הוספת הכפולות הנכונות של השורות האחרות. מכיוון שלכל מונח בביטוי הקובע יש אלמנט אחד מכל שורה, הקובע יהיה אפס זהה. במקרה התלת מימדי, התלות הליניארית של השורות פירושה שהווקטורים המתאימים שוכבים במישור, והמקביל הוא שטוח.

הטיעון האלגברי מכליל בקלות \(n\times n\) לקובעים: הם אפסיים זהים אם השורות תלויות ליניארית.

ההכללה מ \(3\times3\) \(n\times n\) לקובעים היא שהופכת \(\det A=\varepsilon_{ijk}a_{1i}a_{2j}a_{3k}\) ל:

\[ \det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}...a_{np} \tag{2.2.34}\]

איפה \(ijk...p\) מסוכם על כל התמורות של\(132...n\), \(\varepsilon\) והסמל הוא אפס אם שתיים מהסיומות שלו שוות, +1 עבור תמורה שווה ו - 1 עבור תמורה מוזרה. (הערה: כל תמורה יכולה להיכתב כתוצר של החלפות שכנים. ייצוג כזה אינו ייחודי באופן כללי, אך עבור תמורה נתונה, לכל ייצוגים כאלה יהיה מספר אי זוגי של אלמנטים או מספר זוגי.)

משפט חשוב הוא שעבור תוצר של שתי מטריצות\(A\), הקובע \(B\) של המוצר הוא תוצר הקובעים,. \(\det AB=\det A\times \det B\) זה יכול להיות מאומת על ידי כוח הזרוע עבור \(2\times2\) מטריצות, וכן הוכחה במקרה הכללי ניתן למצוא בכל ספר על פיזיקה מתמטית (למשל, ביירון פולר).

ניתן גם להוכיח שאם השורות אינן תלויות באופן ליניארי, הקובע אינו יכול להיות אפס.

(הנה הוכחה: קח \(n\times n\) מטריצה עם וקטורי \(n\) השורה עצמאיים באופן ליניארי. כעת שקול את המרכיבים של אותם וקטורים \(n – 1\) בתת-מרחב הממדי בניצב ל\((1, 0, ... ,0)\). \(n\)וקטורים אלה, שלכל אחד מהם \(n – 1\) רכיבים בלבד, חייבים להיות תלויים ליניארית, מכיוון שיש יותר מהם מממד החלל. כך שנוכל לקחת שילוב כלשהו של השורות שמתחת לשורה הראשונה ולחסר אותה מהשורה הראשונה כדי לעזוב את השורה הראשונה\((a, 0, 0, ... ,0)\), ו- a לא יכול להיות אפס מכיוון שיש לנו מטריצה עם שורות עצמאיות \(n\) ליניאריות. לאחר מכן נוכל לחסר מכפילים של שורה ראשונה זו מהשורות האחרות כדי לקבל קובע שיש אפסים בעמודה הראשונה מתחת לשורה הראשונה. עכשיו תסתכל \(n – 1\) על \(n – 1\) הקובע שיש להכפיל \(a\) אותו.

השורות שלה חייבות להיות עצמאיות ליניארית מכיוון שאלו של המטריצה המקורית היו. עכשיו להמשיך על ידי אינדוקציה.)

כדי לחזור לשלושה ממדים, ברור מהצורה של \[ \det A= a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{31}a_{12}a_{23}-a_{11}a_{32}a_{23}-a_{21}a_{12}a_{33}-a_{31}a_{22}a_{13} \tag{2.2.30}\]

שיכולנו באותה מידה לקחת את העמודות של \(A\) כשלושה וקטורים, \(A=(\vec a_1^C, \vec a_2^C, \vec a_3^C) \) בסימון ברור\(\det A=(\vec a_1^C \times \vec a_2^C)\cdot \vec a_3^C\), ותלות לינארית בין העמודות תבטיח גם את היעלמות הקובע - כך שלמעשה תלות לינארית של העמודות מבטיחה תלות לינארית של השורות.

גם זה מכליל ל\(n\times n\): בהגדרת הקובע\(\det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}...a_{np}\), סיומת השורה קבועה וסיומת העמודה עוברת על כל התמורות המותרות, עם הסימן המתאים - אך אותם מונחים ייווצרו על ידי שמירה על סיומות העמודות בסדר מספרי ומאפשר לסיומת השורה לעבור את התמורות.

בצד: וקטורי סריג הדדיים

אולי כדאי להזכיר כיצד ניתן להבין את ההיפוך של מפעיל \(3\times 3\) מטריצה במונחים של וקטורים. עבור קבוצה של וקטורים עצמאיים ליניארית\((\vec a_1, \vec a_2, \vec a_3)\), \((\vec b_1, \vec b_2, \vec b_3)\) ניתן להגדיר קבוצה הדדית על ידי \[ \vec b_1 =\frac{\vec a_2\times \vec a_3}{\vec a_1\times \vec a_2 \cdot \vec a_3} \tag{2.2.35}\]

וההגדרות המחזוריות הברורות לשני הווקטורים ההדדיים האחרים. אנו רואים מיד את זה \[\vec a_i\cdot \vec b_j =\delta_{ij} \tag{2.2.36}\]

שממנו נובע כי המטריצה ההפוכה ל \[ A=\begin{pmatrix} \vec a_1^R\\ \vec a_2^R \\ \vec a_3^R \end{pmatrix} \; is \; B=\begin{pmatrix}\vec b_1^C& \vec b_2^C& \vec b_3^C\end{pmatrix} \tag{2.2.37}\]

(וקטורים הדדיים אלה חשובים בקריסטלוגרפיה של x -ray, למשל. אם לסריג גבישי יש אטומים מסוימים במיקומים\(n_1\vec a_1 +n_2\vec a_2+n_3\vec a_3\), היכן \(n_1, n_2, n_3\) שיש מספרים שלמים, הווקטורים ההדדיים הם קבוצת הנורמלים למישורים אפשריים של האטומים, ומישורי האטומים הללו הם היסודות החשובים בפיזור ה-x -ray העקיף.)

עצמיות וערכים עצמיים

אם מפעיל \(A\) הפועל על ket \(|V\rangle\) נותן מכפיל מאותו ket, \[ A|V\rangle =\lambda|V\rangle \tag{2.2.38}\]

אז אומרים \(|V\rangle\) שהוא eigenket (או, באותה תדירות, וקטור עצמי, או מצב עצמי!) של \(A\) עם ערך עצמי. \(\lambda\)

ערכים עצמיים וערכים עצמיים הם בעלי חשיבות מרכזית במכניקת הקוונטים: משתנים דינמיים הם אופרטורים, מדידה פיזיקלית של משתנה דינמי מניבה ערך עצמי של האופרטור, ומאלצת את המערכת לתוך eigenket.

בחלק זה נראה כיצד למצוא את הערכים העצמיים ואת החיבורים העצמיים המתאימים למפעיל. \(A\) נשתמש בסימון \(A|a_i\rangle =a_i|a_i\rangle\) עבור קבוצת הגלגלים העצמיים \(|a_i\rangle\) עם הערכים העצמיים המתאימים. \(a_i\) (ברור שבמשוואת הערך העצמי כאן הסיומת לא \(i\) מסוכמת.)

השלב הראשון בפתרון \(A|V\rangle =\lambda|V\rangle\) הוא למצוא את הערכים \(a_i\) העצמיים המותרים.

כתיבת המשוואה בצורה מטריצה: \[ \begin{pmatrix} A_{11}-\lambda & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-\lambda &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-\lambda \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ .\\ .\\ v_n \end{pmatrix} =0 \tag{2.2.39}\]

משוואה זו בעצם אומרת לנו שהעמודות של המטריצה \(A-\lambda I\) תלויות ליניארית! כדי לראות זאת, כתוב את המטריצה כווקטור שורה שכל אלמנט בו הוא אחד העמודות שלו, והמשוואה הופכת \[ (\vec M_1^C,\vec M_2^C,...,\vec M_n^C) \begin{pmatrix} v_1\\ .\\ .\\ .\\ v_n \end{pmatrix}=0 \tag{2.2.40}\]

מה שאומר \[ v_1\vec M_1^C+v_2\vec M_2^C+...+v_n\vec M_n^C=0 \tag{2.2.41}\]

העמודות של המטריצה הן אכן קבוצה תלויה ליניארית.

אנו יודעים שזה אומר שקובע המטריצה \(A-\lambda I\) הוא אפס, \[ \begin{vmatrix} A_{11}-\lambda & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-\lambda &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-\lambda \end{vmatrix}=0 \tag{2.2.42}\]

הערכת הקובע באמצעות \(\det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}....a_{np}\) נותן פולינום \(n^{th}\) סדר הנקרא \(\lambda\) לפעמים פולינום אופייני. כל פולינום יכול להיכתב במונחים של שורשיו: \[ C(\lambda-a_1)(\lambda-a_2)....(\lambda-a_n)=0 \tag{2.2.43}\]

איפה ה- \(a_i\)'s, שורשי הפולינום, \(C\) והוא קבוע כולל, אשר מבדיקת הקובע אנו יכולים לראות שהוא. \((-1)^n\) (זה המקדם של\(\lambda^n\).) השורשים הפולינומיים (שעדיין איננו מכירים) הם למעשה הערכים העצמיים. לדוגמה, לשים \(\lambda=a_1\) את המטריצה,\(\det (A-a_1I)=0\), כלומר \((A-a_1I)|V\rangle=0\) יש פתרון לא טריוויאלי\(|V\rangle\), וזה הווקטור העצמי \(|a_1\rangle\) שלנו.

שימו לב שהמונח האלכסוני בקובע \((A_{11}-\lambda)(A_{22}-\lambda)....(A_{nn}-\lambda)\) מייצר את שני הסדרים המובילים בפולינום\((-1)^n(\lambda^{n}-(A_{11}+...+A_{nn})\lambda^{n-1})\), (וגם כמה מונחים מסדר נמוך יותר). משווה את המקדם של \(\lambda^{n-1}\) 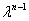כאן לזה ב, \((-1)^n(\lambda-a_1)(\lambda-a_2)....(\lambda-a_n)\) \[ \sum_{i=1}^n a_i=\sum_{i=1}^n A_{ii}= Tr A \tag{2.2.44}\]

לשים \(\lambda=0\) הן את הייצוגים הדטרמיננטיים והן את הפולינום (במילים אחרות, השוואת המונחים הבלתי תלויים), \(\lambda\) \[ \prod_{i=1}^n a_i=\det A \tag{2.2.45}\]

כך שנוכל למצוא גם את הסכום וגם את התוצר של הערכים העצמיים ישירות מהקובע, \(2\times 2\) ולמטריצה זה מספיק כדי לפתור את הבעיה.

עבור כל דבר גדול יותר, השיטה היא לפתור את המשוואה הפולינומית \(\det (A-\lambda I)=0\) כדי למצוא את קבוצת הערכים העצמיים, ולאחר מכן להשתמש בהם כדי לחשב את הווקטורים העצמיים המתאימים. זה נעשה אחד בכל פעם.

תיוג הערך העצמי הראשון שנמצא כ\(a_1\), המשוואה המתאימה לרכיבים \(v_i\) v _i של הווקטור העצמי הוא \(|a_1\rangle\) \[ \begin{pmatrix} A_{11}-a_1 & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-a_1 &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-a_1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ .\\ .\\ v_n \end{pmatrix} =0 \tag{2.2.46}\]

זה נראה כמו \(n\) משוואות \(n\) למספרים\(v_i\), אבל זה לא: זכור שהשורות תלויות לינארית, כך שיש רק משוואות \(n–1\) עצמאיות. עם זאת, זה מספיק כדי לקבוע

היחסים של רכיבי הווקטור\(v_1,...,v_n\), ואז לבסוף הווקטור העצמי מנורמל. התהליך חוזר על עצמו עבור כל eigneערך. (יש צורך בזהירות נוספת אם לפולינום יש שורשים מקבילים - נדון במקרה זה בהמשך.)

ערכים עצמיים ומצבים עצמיים של מטריצות הרמיטיות

עבור מטריצה הרמיטית, קל לקבוע שהערכים העצמיים תמיד אמיתיים. (הערה: הנחה בסיסית של מכניקת הקוונטים, שנדונה בהרצאה הבאה, היא שתצפיות פיזיות מיוצגות על ידי אופרטורים הרמיטיים.) לקחת (בחלק זה) \(A\) להיות הרמיטי\(A=A^{\dagger}\), ולתייג את החלקים העצמיים לפי הערך העצמי, כלומר, \[ A|a_1\rangle=a_1|a_1\rangle \tag{2.2.47}\]

המוצר הפנימי עם החזייה \(\langle a_1|\) נותן\(\langle a_1|A|a_1\rangle=a_1\langle a_1|a_1\rangle\). אבל התוצר הפנימי של המשוואה הצמודה (זוכר\(A=A^{\dagger}\)) \[ \langle a_1|A=a_1^*\langle a_1| \tag{2.2.48}\]

עם \(|a_1\rangle\) נותן\(\langle a_1|A|a_1\rangle=a_1^*\langle a_1|a_1\rangle\), כך\(a_1=a_1^*\), וכל הערכים העצמיים חייבים להיות אמיתיים.

הם בהחלט לא חייבים להיות שונים - למשל, מטריצת היחידה \(I\) היא הרמיטית, וכל הערכים העצמיים שלה הם כמובן 1. אבל בואו קודם לשקול את המקרה שבו הם שונים.

קל להראות שהכבלים העצמיים השייכים לערכים עצמיים שונים הם אורתוגונליים.

אם \[ \begin{matrix} A|a_1\rangle=a_1|a_1\rangle \\ A|a_2\rangle=a_2|a_2\rangle \end{matrix} \tag{2.2.49}\]

קח את החיבור של המשוואה הראשונה ואז את המוצר הפנימי\(|a_2\rangle\), והשווה אותו לתוצר הפנימי של המשוואה השנייה עם\(\langle a_1|\): \[ \langle a_1|A|a_2\rangle=a_1\langle a_1|a_2\rangle=a_2\langle a_1|a_2\rangle \tag{2.2.50}\]

אז \(\langle a_1|a_2\rangle=0\) אלא אם כן הערכים העצמיים שווים. (אם הם שווים, הם מכונים ערכים עצמיים מנוונים.)

הבה נבחן תחילה את המקרה הלא מנוון: \(A\) יש כל הערכים העצמיים מובחנים. החלקים העצמיים של\(A\), מנורמלים כראוי, יוצרים בסיס אורתונורמלי בחלל.

לכתוב \[ |a_1\rangle=\begin{pmatrix} v_{11}\\ v_{21}\\ \vdots\\ v_{n1}\end{pmatrix},\; and\, consider\, the\, matrix\; V=\begin{pmatrix} v_{11}&v_{12}&\dots&v_{1n} \\ v_{21}&v_{22}&\dots&v_{2n}\\ \vdots&\vdots&\ddots&\vdots \\ v_{n1}&v_{n2}&\dots&v_{nn} \end{pmatrix}=\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix} \tag{2.2.51}\]

עכשיו \[ AV=A\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix}=\begin{pmatrix}a_1|a_1\rangle & a_2|a_2\rangle & \dots & a_n|a_n\rangle \end{pmatrix} \tag{2.2.52}\]

כך \[ V^{\dagger}AV=\begin{pmatrix} \langle a_1|\\ \langle a_2|\\ \vdots\\ \langle a_n|\end{pmatrix}\begin{pmatrix}a_1|a_1\rangle & a_2|a_2\rangle & \dots & a_n|a_n\rangle \end{pmatrix}=\begin{pmatrix} a_1&0&\dots&0 \\ 0&a_2&\dots&0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\dots&a_n \end{pmatrix} \tag{2.2.53}\]

שים לב גם כי, כמובן, \(V\) הוא יחידתי: \[ V^{\dagger}V=\begin{pmatrix} \langle a_1|\\ \langle a_2|\\ \vdots\\ \langle a_n|\end{pmatrix}\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix}=\begin{pmatrix} 1&0&\dots&0 \\ 0&1&\dots&0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\dots&1\end{pmatrix} \tag{2.2.54}\]

קבענו, אם כן, כי עבור מטריצה הרמיטית עם ערכים עצמיים מובהקים (מקרה לא מנוון), המטריצה היחידה \(V\) בעלת עמודים זהים לכבלים העצמיים המנורמלים של אלכסונים, כלומר היא אלכסונית. \(A\) \(A\) \(V^{\dagger}AV\) יתר על כן, האלמנטים (האלכסוניים) שלו שווים לערכים העצמיים המתאימים של. \(A\)

דרך נוספת לומר זאת היא שהמטריצה היחידה \(V\) היא הטרנספורמציה מהבסיס האורתונורמלי המקורי במרחב הזה לבסיס שנוצר מהחלקים העצמיים המנורמלים של. \(A\)

הוכחה לכך שהווקטורים העצמיים של מטריצה הרמיטית משתרעים על החלל

נעבור כעת למקרה הכללי: מה אם חלק מהערכים העצמיים של \(A\) זהים? במקרה זה, כל שילוב ליניארי ביניהם הוא גם וקטור עצמי עם אותו ערך עצמי. בהנחה שהם מהווים בסיס בתת-חלל, ניתן להשתמש בהליך גראם שמידט כדי להפוך אותו לאורתונורמלי, וכך לחלק מבסיס אורתונורמלי של החלל כולו.

עם זאת, למעשה לא קבענו שהווקטורים העצמיים אכן מהווים בסיס בתת-מרחב מנוון. האם יכול להיות ש (אם ניקח את המקרה הפשוט ביותר) שני הווקטורים העצמיים של הערך העצמי היחיד מתגלים כמקבילים? זה למעשה המקרה של כמה \(2\times2\) מטריצות - למשל, עלינו להוכיח שזה לא נכון לגבי מטריצות הרמיטיות\(\begin{pmatrix}1&1\\0&1\end{pmatrix}\), וגם ההצהרות האנלוגיות לתת-מרחבים מנווונים בממדים גבוהים יותר.

מצגת ברורה ניתנת בביירון ופולר, סעיף 4.7. אנו עוקבים אחריו כאן. ההליך הוא על ידי אינדוקציה \(2\times2\) מהמקרה. למטריצה \(2\times2\) ההרמיטית הכללית יש את הצורה \[ \begin{pmatrix}a&b\\b^*&c\end{pmatrix} \tag{2.2.55}\]

איפה\(a\), \(c\) הם אמיתיים. קל לבדוק שאם הערכים העצמיים מנוונים, מטריצה זו הופכת לכפולה אמיתית של הזהות, ולכן באופן טריוויאלי יש שני וקטורים עצמיים אורתונורמליים. מכיוון שאנו כבר יודעים שאם הערכים העצמיים של מטריצה \(2\times2\) הרמיטית נבדלים זה מזה ניתן באלכסון על ידי הטרנספורמציה היחידה שנוצרת מהווקטורים העצמיים האורתונורמליים שלה, קבענו שכל מטריצה הרמיטית יכולה להיות אלכסונית כל כך. \(2\times2\)

כדי לבצע את תהליך האינדוקציה, אנו מניחים כעת שכל מטריצה \((n-1)\times(n-1)\) הרמיטית יכולה להיות אלכסונית על ידי טרנספורמציה יחידה. אנחנו צריכים להוכיח שזה אומר שזה נכון גם לגבי מטריצה \(n\times n\) הרמיטית. \(A\) (כזכור, טרנספורמציה יחידה לוקחת בסיס אורתונורמלי שלם אחד למשנהו. אם הוא מאלכסן מטריצה הרמיטית, הבסיס החדש הוא בהכרח קבוצת הווקטורים העצמיים האורתונורמליים. מכאן שאם ניתן לאלכסון את המטריצה, הווקטורים העצמיים אכן משתרעים על המרחב הממדי n.)

בחר ערך עצמי \(a_1\) של\(A\), עם וקטור עצמי מנורמל. \(|a_1\rangle=(v_{11},v_{21},....,v_{n1})^T\) (הכנסנו \(T\) לשינוי, כדי לחסוך את הסרבול של מילוי הדף בכמה וקטורי עמודות.) אנו בונים אופרטור יחידתי \(V\) על ידי הפיכת העמודה הראשונה, ולאחר מכן מילוי עם וקטורים מנורמלים \(n-1\) אחרים כדי לבנות, עם\(|a_1\rangle\), בסיס אורתונורמלי n ממדי.

כעת\(A|a_1\rangle=a_1|a_1\rangle\), מכיוון שהעמודה הראשונה של המטריצה \(AV\) תהיה פשוט\(a_1|a_1\rangle\), ושורות המטריצה \(V^{\dagger}=V^{-1}\) יבואו \(\langle a_1|\) אחריהם וקטורים \(n-1\) מנורמלים אורתוגונליים אליה, כך שהעמודה הראשונה של המטריצה \(V^{\dagger}AV\) תהיה \(a_1\) אחריה אפסים. קל לבדוק כי הוא הרמיטי, שכן \(V^{\dagger}AV\) הוא, כך השורה הראשונה שלה \(A\) היא גם אפס מעבר למונח האלכסוני הראשון.

זה קובע כי עבור מטריצה \(n\times n\) הרמיטית, קיימת טרנספורמציה יחידה בכדי להכניס אותה לצורה: \[ V^{\dagger}AV=\begin{pmatrix} a_1 &0&.&.&0\\ 0& M_{22}&.&.&M_{2n} \\ 0&.&.&.&. \\ 0&.&.&.&. \\ 0 &M_{n2}&.&.& M_{nn} \end{pmatrix} \tag{2.2.56}\]

אך כעת אנו יכולים לבצע טרנספורמציה יחידה שנייה באורתוגונל \((n-1)\times(n-1)\) התת-חלל ל \(|a_1\rangle\) (זה כמובן משאיר \(|a_1\rangle\) בלתי משתנה), להשלמת האלכסון המלא - כלומר קיום האלכסון, בתוספת הטיעון לעיל, מבטיח את קיומו של \((n-1)\times(n-1)\) האלכסון: האינדוקציה הושלמה. \(n\times n\)

אלכסון מטריקס הרמיטי

כפי שנדון לעיל, מטריצה הרמיטית היא אלכסונית בבסיס האורתונורמלי של קבוצת הווקטורים העצמיים שלה:, מאז \(|a_1\rangle,|a_2\rangle,...,|a_n\rangle\) \[ \langle a_i|A|a_j\rangle=\langle a_i|a_j|a_j\rangle=a_j\langle a_i|a_j\rangle=a_j\delta_{ij} \tag{2.2.57}\]

אם נותנים לנו את מרכיבי המטריצה של \(A\) בבסיס אורתונורמלי אחר, כדי לאלכסן אותו עלינו לסובב מהבסיס האורתונורמלי הראשוני לכזה המורכב מהעצמיות של. \(A\)

מציין את הבסיס האורתונורמלי הראשוני בצורה הסטנדרטית \[ |1\rangle=\begin{pmatrix} 1\\0\\0\\ \vdots\\0\end{pmatrix}, \; |2\rangle=\begin{pmatrix} 0\\1\\0\\ \vdots\\0\end{pmatrix}, \; |i\rangle=\begin{pmatrix} 0\\ \vdots\\ 1\\ \vdots\\0\end{pmatrix}... \; (1\, in\, i^{th}\, place\, down), \; |n\rangle=\begin{pmatrix} 0\\0\\0\\ \vdots\\1\end{pmatrix} \tag{2.2.58}\]

האלמנטים של המטריצה הם\(A_{ij}=\langle i|A|j\rangle\).

טרנספורמציה מבסיס אורתונורמלי אחד למשנהו היא טרנספורמציה יחידה, כפי שנדון לעיל, ולכן אנו כותבים אותה \[ |V\rangle \to |V'\rangle=U|V\rangle \tag{2.2.59}\]

תחת טרנספורמציה זו, אלמנט המטריצה \[ \langle W|A|V\rangle \to \langle W'|A|V'\rangle=\langle W|U^{\dagger}AU|V\rangle \tag{2.2.60}\]

כך שנוכל למצוא את מטריצת הטרנספורמציה המתאימה \(U\) על ידי דרישה שהיא \(U^{\dagger}AU\) תהיה אלכסונית ביחס למערך המקורי של וקטורי הבסיס. (שינוי האופרטור בדרך זו, השארת המרחב הווקטורי לבדו, שווה לסיבוב המרחב הווקטורי ולהשאיר את המפעיל לבדו. כמובן שבמערכת עם יותר ממפעיל אחד, יהיה צורך להחיל את אותה טרנספורמציה על כל המפעילים).

למעשה, בדיוק כפי שדנו במקרה הלא מנוון (ערכים עצמיים מובהקים), המטריצה היחידה \(U\) שאנו זקוקים לה מורכבת רק מהחלקים העצמיים המנורמלים של המפעיל, \(A\) \[ U=(|a_1\rangle,|a_2\rangle,...,|a_n\rangle) \tag{2.2.61}\]

וזה כדלקמן כמו קודם \[ (U^{\dagger}AU)_{ij}=\langle a_i|a_j|a_j\rangle=\delta_{ij}a_j, \; a\, diagonal\, matrix. \tag{2.2.62}\]

(הסיומות החוזרות כאן כמובן אינן מסוכמות.)

אם חלק מהערכים העצמיים זהים, ייתכן שיהיה צורך בהליך גראם שמידט כדי ליצור קבוצה אורתוגונלית, כפי שהוזכר קודם לכן.

פונקציות של מטריצות

אותו מפעיל יחידתי \(U\) שמאלכסן מטריצה הרמיטית \(A\) יתלכסן גם הוא מכיוון \(A^2\) \[ U^{-1}A^2U=U^{-1}AAU=U^{-1}AUU^{-1}AU \tag{2.2.63}\]

כך \[ U^{\dagger}A^2U=\begin{pmatrix} a_1^2&0&0&.&0 \\ 0&a_2^2&0&.&0\\ 0&0&a_3^2&.&0 \\ .&.&.&.&. \\ 0&.&.&.&a_n^2\end{pmatrix} \tag{2.2.64}\]

ככל הנראה, אותו תהליך פועל עבור כל כוח של\(A\), ובאופן רשמי עבור כל פונקציה \(A\) הניתנת לביטוי כסדרת כוח, אך כמובן שיש לקחת בחשבון מאפייני התכנסות, וזה הופך להיות מסובך יותר במעבר ממטריצות סופיות למפעילים במרחבים אינסופיים.

מטריצות הרמיטיות נוסעות

מהאמור לעיל, מערך הכוחות של מטריצה הרמיטית כולם נוסעים זה עם זה, ויש להם קבוצה משותפת של וקטורים עצמיים (אך לא אותם ערכים עצמיים, כמובן). למעשה לא קשה להראות שלכל שתי מטריצות הרמיטיות שנוסעות זו עם זו יש אותה קבוצה של וקטורים עצמיים (לאחר סידורים אפשריים של גראם שמידט בתת-מרחבים מנווונים).

אם שתי מטריצות \(n\times n\) הרמיטיות\(A\), \(B\) נוסעים, כלומר, \(A\) ויש להם קבוצה לא מנוונת של וקטורים עצמיים\(AB=BA\), אז\(A|a_i\rangle=a_i|a_i\rangle\), כלומר\(AB|a_i\rangle=BA|a_i\rangle=Ba_i|a_i\rangle=a_iB|a_i\rangle\), הוא וקטור עצמי של עם ערך עצמי. \(B|a_i\rangle\) \(A\) \(a_i\) מכיוון שאינו \(A\) מנוון, \(B|a_i\rangle\) חייב להיות מספר רב של\(|a_i\rangle\), ואנו מסיקים כי\(A\), \(B\) יש את אותה קבוצה של וקטורים עצמיים.

כעת נניח \(A\) שהוא מנוון, ושקול את \(m\times m\) תת-המרחב \(S_{a_i}\) המשתרע על ידי הווקטורים \(|a_i,1\rangle,\; |a_i,2\rangle,...\) העצמיים שיש להם ערך עצמי. \(A\) \(a_i\) החלת הטיעון בפסקה לעיל, \(B|a_i,1\rangle,\; B|a_i,2\rangle,...\) חייבת להיות טמונה גם בתת-מרחב זה. לכן, אם נשתנה באותה טרנספורמציה יחידה שאלכסונית\(A\), באופן כללי לא \(B\) תהיה אלכסונית בתת-המרחב\(S_{a_i}\), אלא זה יהיה מה שמכונה בלוק אלכסוני, בכך שאם \(B\) פועל על וקטור כלשהו \(S_{a_i}\) בו הוא נותן וקטור פנימה. \(B\) \(S_{a_i}\)

\(B\)ניתן לכתוב כשני בלוקים אלכסוניים: אחד\(m\times m\), אחד\((n-m)\times (n-m)\), עם אפסים מחוץ לבלוקים האלכסוניים האלה, למשל, עבור\(m=2,\; n=5\): \[ \begin{pmatrix} b_{11}&b_{12}&0&0&0 \\ b_{21}&b_{22}&0&0&0 \\ 0&0&b_{33}&b_{34}&b_{35} \\ 0&0&b_{43}&b_{44}&b_{45} \\ 0&0&b_{53}&b_{54}&b_{55} \end{pmatrix} \tag{2.2.65}\]

ולמעשה, אם יש רק ערך עצמי מנוון אחד, לבלוק השני יהיו מונחים שאינם אפסיים באלכסון: \[ \begin{pmatrix} b_{11}&b_{12}&0&0&0 \\ b_{21}&b_{22}&0&0&0 \\ 0&0&b_3&0&0 \\ 0&0&0&b_4&0 \\ 0&0&0&0&b_5 \end{pmatrix} \tag{2.2.65}\]

\(B\)לכן פועל על שני תת-מרחבים, אחד m -ממדי, אחד (n - m) -ממדי, באופן עצמאי - וקטור כולו בתת-מרחב אחד נשאר שם.

המשמעות היא שנוכל להשלים את האלכסון של \(B\) עם מפעיל יחידתי שפועל רק על \(m\times m\) הבלוק. \(S_{a_i}\) אופרטור כזה ישפיע גם על הווקטורים העצמיים של\(A\), אבל זה לא משנה, מכיוון שכל הווקטורים בתת-מרחב זה הם וקטורים עצמיים \(A\) בעלי אותו ערך עצמי, כך שמבחינתנו נוכל לבחור כל בסיס אורתונורמלי \(A\) שנאהב - וקטורי הבסיס עדיין יהיו וקטורים עצמיים.

זה קובע כי ניתן לאלכסון כל שתי מטריצות הרמיטיות נוסעות בו זמנית. ברור שזה לעולם לא יכול להיות נכון לגבי מטריצות שאינן נוסעות, מכיוון שכל המטריצות האלכסוניות נוסעות.

אלכסון מטריקס יחידתי

כל מטריצה יחידה יכולה להיות אלכסונית על ידי טרנספורמציה יחידה. כדי לראות זאת, זכור כי \(M\) ניתן לכתוב כל מטריצה כסכום של מטריצה הרמיטית ומטריצה אנטי הרמיטית, \[ M=\frac{M+M^{\dagger}}{2}+\frac{M-M^{\dagger}}{2}=A+iB \tag{2.2.66}\]

שבו שניהם \(A,\; B\) הרמיטים. זהו אנלוגי המטריצה של כתיבת מספר מורכב שרירותי כסכום של חלקים אמיתיים ודמיוניים.

אם הם \(A,\; B\) נוסעים, הם יכולים להיות באלכסון בו זמנית (ראה את החלק הקודם), ולכן \(M\) ניתן באלכסון. כעת, אם מטריצה יחידה באה לידי ביטוי בצורה זו \(U=A+iB\) עם \(A,\; B\) הרמיטיאן, היא נובעת בקלות מאותה \(A,\; B\) נסיעה, כך \(UU^{\dagger}=U^{\dagger}U=1\) שניתן לאלכסון כל מטריצה יחידה על ידי \(U\) טרנספורמציה יחידה. באופן כללי יותר, אם מטריצה \(M\) נוסעת עם הצמוד שלה\(M^{\dagger}\), ניתן לאלכסון אותה.

(הערה: לא ניתן לבצע אלכסון \(M\) אלא אם כן \(A,\; B\) שניהם אלכסוניים בו זמנית. זה נובע \(U^{\dagger}AU,\; U^{\dagger}iBU\) מהיותם הרמיטיים ואנטי-הרמיטיים עבור כל מפעיל יחידתי\(U\), כך שהאלמנטים הלא-אלכסוניים שלהם אינם יכולים לבטל זה את זה, כולם חייבים להיות אפס אם M עבר אלכסון על ידי\(U\), ובמקרה זה שתי המטריצות שהשתנו \(U^{\dagger}AU,\; U^{\dagger}iBU\) הן אלכסוניות, ולכן נסיעות, וכך גם המטריצות המקוריות.) \(A,\; B\)

כדאי להסתכל על דוגמה ספציפית, סיבוב פשוט של בסיס אורתונורמלי אחד למשנהו בשלושה ממדים. ברור שהציר דרך המקור שעליו מסתובב הבסיס הוא וקטור עצמי של הטרנספורמציה. פחות ברור מה יכולים להיות שני הווקטורים העצמיים האחרים - או, באופן שווה, מהם הווקטורים העצמיים המתאימים לסיבוב בסיס דו מימדי במישור? הדרך לגלות זאת היא לרשום את המטריצה ולאלכסון אותה.

המטריצה \[ U(\theta)=\begin{pmatrix} \cos \theta &\sin \theta\\ -\sin \theta &\cos \theta\end{pmatrix} \tag{2.2.67}\]

שים לב כי הקובע שווה לאחדות. הערכים העצמיים ניתנים על ידי פתרון \[ \begin{vmatrix} \cos \theta -\lambda &\sin \theta\\ -\sin \theta &\cos \theta -\lambda\end{vmatrix}=0\; to\, give\; \lambda=e^{\pm i\theta} \tag{2.2.68}\]

הווקטורים העצמיים המתאימים מספקים

\[ \begin{pmatrix} \cos \theta &\sin \theta\\ -\sin \theta &\cos \theta\end{pmatrix}\dbinom{u_1^{\pm}}{u_2^{\pm}}=e^{\pm i\theta}\dbinom{u_1^{\pm}}{u_2^{\pm}} \tag{2.2.69}\]

הווקטורים העצמיים, מנורמלים, הם: \[ \dbinom{u_1^{\pm}}{u_2^{\pm}}=\frac{1}{\sqrt{2}}\dbinom{1}{\pm i} \tag{2.2.70}\]

שים לב שבניגוד למטריצה הרמיטית, הערכים העצמיים של מטריצה יחידה אינם חייבים להיות אמיתיים. למעשה, מ-\(U^{\dagger}U=1\), דחוק בין החזייה לקט של וקטור עצמי, אנו רואים שכל ערך עצמי של מטריצה יחידה חייב להיות מודול יחידה - זהו מספר מורכב במעגל היחידה. במבט לאחור, היינו צריכים להבין שערך עצמי אחד של סיבוב דו מימדי צריך להיות\(e^{i\theta}\), תוצר של שני סיבובים דו מימדיים ניתן להוסיף את זוויות הסיבוב, וסיבוב דרך \(\pi\) משנה את כל הסימנים, כך יש ערך עצמי. \(-1\) שים לב שהווקטור העצמי עצמו אינו תלוי בזווית הסיבוב - הסיבובים כולם נוסעים, ולכן עליהם להיות בעלי וקטורים עצמיים משותפים. מפעילי סיבוב עוקבים המוחלים על הווקטור העצמי פלוס מוסיפים את הזוויות שלהם, כאשר הם מוחלים על וקטור העצמי מינוס, כל הזוויות מופחתות.

תורם

• Template:ContribFowler